1 Introduction

Because they are used in practical sciences, nonlinear partial differential equations (NLPDEs) are quite important. In various physical or applied domains, including quantum physics, fluid mechanics, applied chemistry, optics, and many more, NLPDEs always represent some nonlinear physical phenomena. In the structures of mathematical NLPDEs, the nonlinear Schrödinger equations (NLSE) are some significant model equations that represent the physical phenomena. Furthermore, FDEs are the generalized versions of nonlinear fractional differential equations (NLFDEs). For example, Two-Sided Beta Time Fractional Korteweg–de Vries Equations (Akter et al. 2023), space fractional parameter on nonlinear ion acoustic shock wave excitation (Uddin et al. 2022b), fractional resonant nonlinear Schrodinger equations (Hafez et al. 2019), beta derivative spatial–temporal evolution (Uddin et al. 2021; Uddin and Hafez 2020), Heisenberg model of ferromagnetic spin chains with beta derivative evolution (Uddin et al. 2022c), space–time fractional cubic–quartic nonlinear Schrödinger equation (Uddin et al. 2022a). The most crucial objective is to use some trustworthy methods to determine their approximative and analytical solutions. The precise solitary wave solutions of any FDE, among other types of solutions, are very important for understanding the related physics. Bilinear residual network method (Zhang and Li 2022) and Bilinear neural network method (Zhang and Bilige 2019; Zhang et al. 2021a, b) can obtain accurate analytical solution for partial differential equation, which is far more accurate than traditional neural network numerical method. The NLFDE wave solutions have been secured using a variety of analytical techniques (Hosseini et al. 2020; Kudryashov 2020; Bekir 2008; Rezazadeh et al. 2019; Wang et al. 2021; Shen and Tian 2021; Gao et al. 2021a; Yang et al. 2021; Gao et al. 2021b, c, d; Gao et al. 2021; Khatun et al. 2022; Arefin et al. 2022; Zaman et al. 2023a, b, c; Volkan 2023; Iqbal et al. 2022; Shen et al. 2021, 2022, Zou and Guo 2023; Song et al. 2020; Li et al. 2023; Li and Guo 2023; Yang et al. 2018; Guo et al. 2020). The periodic type wave solutions to the Kundu–Mukherjee–Naskar (KMN) equation in \((2+1)-\)-dimension have been investigated using the variational principle method (He 2020). In the field of optics, the Riccati equation method (Malomed et al. 2005) has also been used to secure a number of optical solitons.

The MEWE is a different significant model. By using diverse methodologies, various soliton solutions have been discovered (Zafar et al. 2020; Malfliet 1992; Raslan et al. 2017; Shi and Zhang 2019; Atangana et al. 2016; Atangana and Alqahtani 2016; Yépez-Martínez et al. 2018; Yusuf et al. 2019; Uddin et al. 2021; Ghanbari and Gómez-Aguilar 2019; Arshed 2020; Arshad et al. 2019; Raza et al. 2019; Akram et al. 2018; Hosseini et al. 2017). The fractional BTD has a few useful properties that are listed in Yépez-Martínez et al. (2018), Yusuf et al. (2019), Uddin et al. (2021), Ghanbari and Gómez-Aguilar (2019) and Zaman et al. (2023d).

Finding soliton solutions to the MEWE with BTD is the primary goal of this study. To complete the aforementioned work, the beta derivative is used in conjunction with the \(\exp (-\phi (\eta ))\) method and the \(Exp_a\)-function approaches.

2 Description of model

The modified equal width equation is a class of FPDE describing optics, solid-state physics and hydro-magnetic waves in cold plasma. This model is used as a model in partial differential equations for the simulation of one-dimensional wave transmission in nonlinear media with dispersion processes. This equation plays a significant role in fluid mechanics. The MEWE (Shi and Zhang 2019; Islam et al. 2020) is given:

$$\begin{aligned} \frac{\partial ^{\beta }q}{\partial t^{\beta }}+\theta \frac{\partial q^{3}}{\partial x}-\rho \frac{\partial ^{2} }{\partial x^{2}}\left( \frac{\partial ^{\beta } q}{\partial t^{\beta }}\right) =0. \end{aligned}$$
(1)

where \(\theta\) and \(\rho\) are parameters.

We take travelling wave transformations:

$$\begin{aligned} q(x, t)=Q(\eta ), ~~\eta =\omega x - \frac{\lambda }{\beta } \left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta } \end{aligned}$$
(2)

where \(\omega\) and \(\lambda\) are the constants.

The use of Eq. (2) into the Eq. (1), yields the ordinary differential equation (ODE):

$$\begin{aligned} -\lambda Q^{'}+\theta \omega (Q^{3})^{'}+\rho \lambda \omega ^{2} Q^{'''}=0. \end{aligned}$$
(3)

From Eq. (3) with respect to \(\eta\), we acquire

$$\begin{aligned} -\lambda Q +\theta \omega Q^{3}+\rho \lambda \omega ^{2} Q^{''}=0. \end{aligned}$$
(4)

2.1 Explanation of the \(Exp(-\phi (\eta ))\) method

The \(Exp(-\phi (\eta ))\) method is given by the following steps (Arshed 2020).

Step 1

$$\begin{aligned} G ( q_{t}, q^{2}q_t, q_{x}, q_{tt}, q_{xx}, q_{x t},\ldots )=0, \end{aligned}$$
(5)

where \(q=q(x, t)\) depend on x and t and is a differentiable function. Now assume the given wave transformation:

$$\begin{aligned} q(x,t)=Q(\eta ), ~~\eta =-\mu t+x \end{aligned}$$
(6)

where \(\mu\) is the wave speed. Putting the Eq. (6) into Eq. (5), taking the below nonlinear ordinary differential equation (NODE):

$$\begin{aligned} F(Q, Q^2 Q^{'}, Q^{''}, Q^{'''} ,\ldots )=0. \end{aligned}$$
(7)

The Eq. (7) has the following solutions by the \(\exp (-\phi (\eta ))\) method:

Step 2 We look for answers to Eq. (7) in the following format:

$$\begin{aligned} Q(\eta )=\sum _{j=0}^{m}\alpha _{j} \exp (-\phi (\eta ))^{j}, \end{aligned}$$
(8)

here \(\alpha _{j}\) \(\ne 0\) to be found.

The function \(\phi (\eta )\) fulfil the below auxiliary differential equation:

$$\begin{aligned} \phi '(\eta )=\exp (-\phi (\eta ))+A \exp (\phi (\eta ))+B. \end{aligned}$$
(9)

Equation (9) gives the following solution.

Case 1: If \(B^{2}-4A>0\) and \(A\ne 0\),

$$\begin{aligned} \phi _{1}(\eta )=\ln \left( \frac{-\sqrt{B^{2}- 4 A} \tanh \left( \frac{\sqrt{B^{2}- ~4~ A}}{2}(\eta +C)\right) -B}{2 A}\right) , \end{aligned}$$
(10)

Case 2: If \(B^{2}-4A<0\) and \(A\ne 0\),

$$\begin{aligned} \phi _{2}(\eta )=\ln \left( \frac{\sqrt{ 4 A - B^{2}} \tan \left( \frac{\sqrt{ 4 A - B^{2}}}{2}(\eta +C)\right) -B}{2 A}\right) , \end{aligned}$$
(11)

Case 3: If \(B^{2}-4A>0\) , \(A=0\) and \(B\ne 0\),

$$\begin{aligned} \phi _{3}(\eta )=-\ln \left( \frac{B}{\cosh (B(\eta +C))+\sinh (B(\eta +C))-1}\right) , \end{aligned}$$
(12)

Case 4: If \(B^{2}-4A=0\) , \(A\ne 0\) and \(B\ne 0\),

$$\begin{aligned} \phi _{4}(\eta )=\ln \left( -\frac{2(B(\eta +C))+2}{B^{2}(\eta +C)}\right) , \end{aligned}$$
(13)

Case 5:

If \(B^{2}-4A=0\) , \(A=0\) and \(B=0\),

$$\begin{aligned} \phi _{5}(\eta )=\ln \left( \eta +C \right) , \end{aligned}$$
(14)

here C is the integration constant.

Step 3 The positive integer ‘m’ will be calculated with the help of homogenous balance technique (HBT) between the highest derivative and the non-linear term in the Eq. (7).

We will obtain the solutions of the NLPDE Eq. (5) by using the above steps.

2.2 Solutions with the \(Exp(-\phi (\eta ))\) method

Balancing the terms \(Q^{3}\) and \(Q^{''}\) in Eq. (4) by homogeneous technique, we acquire \(m=1\). For \(m=1\), Eq. (8) yields

$$\begin{aligned} Q(\eta )=\alpha _{0}+\alpha _{1} \exp (-\phi (\eta )), \end{aligned}$$
(15)

Here \(\alpha _0\) and \(\alpha _1\) are unknown parameters. A polynomial in powers of \(\phi\) is produced when the Eqs. (15) and (9) are combined in the Eq. (4). We acquire a set of equations by setting the coefficients for each power and constant term to be equal to 0. Using Mathematica, we discover:

Set 1:

$$\begin{aligned} \left\{ \alpha _0=-\frac{ B \sqrt{-\lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }},\alpha _1=-\frac{ \sqrt{2} \sqrt{-\lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{\theta }},A=\frac{B^2 \rho \omega ^2+2}{4 \rho \omega ^2}\right\} , \end{aligned}$$
(16)

Case 1:

If \(B^{2}-4A>0\) and \(A\ne 0\),

$$\begin{aligned} q_1(x, t )=-\frac{ \sqrt{- \lambda } }{\sqrt{2} \sqrt{\theta } \sqrt{\rho } ~\omega ^{3/2}}\left( B \rho \omega ^2-\frac{B^2 \rho \omega ^2+2}{B+\sqrt{\frac{-2}{\rho \omega ^2}} ~\tanh \left( (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } ) \sqrt{\frac{-1}{2 \rho \omega ^2}}\right) }\right) , \end{aligned}$$
(17)
Fig. 1
figure 1

Graph of \((Exp(-\phi (\eta ))\) Method) Set 1, Case 1 \(\lambda =-0.3,\rho =1,\beta =1,\theta =2,B=0.5, -10<x<10, 0<t<2\)

Full size image
Fig. 2
figure 2

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 1 \(\lambda =-0.3,\rho =1,t=1,\theta =2,B=0.5, -10<x<10\)

Full size image
Fig. 3
figure 3

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 1 \(\lambda =-0.3,\rho =1,\theta =2,B=0.5, -10<x<10, 0<t<2\)

Full size image

Case 2:

If \(B^{2}-4A<0\) and \(A\ne 0\),

$$\begin{aligned} q_2(x, t )=-\frac{ \sqrt{- \lambda } }{\sqrt{2} \sqrt{\theta } \sqrt{\rho } \omega ^{3/2}}\left( B \rho \omega ^2+\frac{B^2 \rho \omega ^2+2}{-B+\sqrt{\frac{2}{\rho \omega ^2}} \tan \left( (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } ) \sqrt{\frac{1}{2 \rho \omega ^2}}\right) }\right) \end{aligned}$$
(18)
Fig. 4
figure 4

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 2 \(\lambda =-0.2,\rho =1,\beta =1,\theta =2,B=0.5, -10<x<10, 0<t<2\)

Full size image
Fig. 5
figure 5

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 2 \(\lambda =-0.2,\rho =1,t=1,\theta =2,B=0.5, -10<x<10\)

Full size image
Fig. 6
figure 6

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 2 \(\lambda =-0.2,\rho =1,\theta =2,B=0.5, -10<x<10, 0<t<2\)

Full size image

Case 3:

If \(B^{2}-4A>0\) , \(A=0\) and \(B\ne 0\),

$$\begin{aligned} q_3(x, t )=-\frac{ B \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }}~\coth \left( \frac{1}{2} B (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } )\right) , \end{aligned}$$
(19)
Fig. 7
figure 7

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 3 \(\lambda =-1, \rho =1.5, \beta =1, \theta =2, B=0.5,-10<x<10, 0<t<2\)

Full size image
Fig. 8
figure 8

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 3 \(\lambda =-1, \rho =1.5, t=1, \theta =2, B=0.5, -10<x<10\)

Full size image
Fig. 9
figure 9

Graph of (\(Exp(-\phi (\eta ))\) Method) Set 1, Case 3 \(\lambda =-1, \rho =1.5, \theta =2, B=0.5, -10<x<10, 0<t<2\)

Full size image

Case 4:

If \(B^{2}-4A=0\) , \(A\ne 0\) and \(B\ne 0\),

$$\begin{aligned} q_4(x, t )=-\frac{ B \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }} \left( \frac{1}{(B (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } )+1)}\right) , \end{aligned}$$
(20)

Case 5:

If \(B^{2}-4A=0\), \(A=0\) and \(B=0\),

$$\begin{aligned} q_5(x, t )=-\frac{ \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }}\left( B+\frac{2}{C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } }\right) , \end{aligned}$$
(21)

Set 2:

$$\begin{aligned} \left\{ \alpha _0=\frac{ B \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }},\alpha _1=\frac{i \sqrt{2} \sqrt{\lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{\theta }},A=\frac{B^2 \rho \omega ^2+2}{4 \rho \omega ^2}\right\} , \end{aligned}$$
(22)

Case 1:

If \(B^{2}-4A>0\) and \(A\ne 0\),

$$\begin{aligned} q_1(x, t )=\frac{ \sqrt{- \lambda } }{\sqrt{2} \sqrt{\theta } \sqrt{\rho } ~\omega ^{3/2}}\left( B \rho \omega ^2-\frac{B^2 \rho \omega ^2+2}{B+\sqrt{\frac{-2}{\rho \omega ^2}} ~\tanh \left( (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } ) \sqrt{\frac{-1}{2 \rho \omega ^2}}\right) }\right) , \end{aligned}$$
(23)

Case 2:

If \(B^{2}-4A<0\) and \(A\ne 0\),

$$\begin{aligned} q_2(x, t )=\frac{ \sqrt{- \lambda } }{\sqrt{2} \sqrt{\theta } \sqrt{\rho } \omega ^{3/2}}\left( B \rho \omega ^2+\frac{B^2 \rho \omega ^2+2}{-B+\sqrt{\frac{2}{\rho \omega ^2}} \tan \left( (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } ) \sqrt{\frac{1}{2 \rho \omega ^2}}\right) }\right) , \end{aligned}$$
(24)

Case 3:

If \(B^{2}-4A>0\) , \(A=0\) and \(B\ne 0\),

$$\begin{aligned} q_3(x, t )=\frac{ B \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }}~\coth \left( \frac{1}{2} B (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } )\right) , \end{aligned}$$
(25)

Case 4:

If \(B^{2}-4A=0\) , \(A\ne 0\) and \(B\ne 0\),

$$\begin{aligned} q_4(x, t )=\frac{ B \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }} \left( \frac{1}{(B (C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } )+1)}\right) , \end{aligned}$$
(26)

Case 5:

If \(B^{2}-4A>0\) , \(A=0\) and \(B=0\),

$$\begin{aligned} q_5(x, t )=\frac{ \sqrt{- \lambda } \sqrt{\rho } \sqrt{\omega }}{\sqrt{2} \sqrt{\theta }}\left( B+\frac{2}{C+\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta } }\right) , \end{aligned}$$
(27)

2.3 Explanation of the \(Exp_a\) function method

We regard Eqs. (5)–(7). We assume that Eq. (7) has the following solution (Zayed and Al-Nowehy 2017; Zafar 2019):

$$\begin{aligned} Q(\eta )=\frac{\alpha _0+\alpha _1 D^{\eta }+\cdots +\alpha _m D^{m \eta }}{\beta _0+\beta _1 D^{\eta }+ \cdots +\beta _m d^{m \eta } },~~\alpha \ne 0,1. \end{aligned}$$
(28)

here \(\alpha _{j}\) and \(\beta _{j} (0\le j\le m)\) are unknown parameters and to be find later. The positive integer m is determined by using HBT into Eq. (7). Inserting Eq. (28) into Eq. (7), yield

$$\begin{aligned} \wp (D^\eta )=\ell _0+\ell _1 D^\eta +\cdots +\ell _t D^{t\eta } =0. \end{aligned}$$
(29)

Putting \(\ell _j~(0\le j\le t)\) into Eq. (7) equal to zero, so we acquire.

$$\begin{aligned} \ell _j=0, \quad \quad \quad \quad where ~~j=0,\ldots ,t. \end{aligned}$$
(30)

We achieve the wave soltions of Eq. (5).

2.4 Solutions with the \(Exp_a\) function method

Balancing the terms \(Q^{3}\) and \(Q^{''}\) into the Eq. (4) by homogeneous technique, we acquire \(m=1\). For \(m=1\), Eq. (28) reduces into:

$$\begin{aligned} Q(\eta )=\frac{\alpha _0+\alpha _1 D^{\eta }}{\beta _0+\beta _1 D^{\eta }}, \end{aligned}$$
(31)

where \(\alpha _0\), \(\alpha _1\) , \(\beta _0\) and \(\beta _1\) are unknowns. A set of equations is acquired by entering Eq. (31) into the Eq. (4) and setting the coefficients of each power and constant term to 0. Using Mathematica, we discover:

Set 1:

$$\begin{aligned} \left\{ \alpha _0=\mp \frac{\root 4 \of {-\frac{1}{2}} \sqrt{\lambda } \root 4 \of {\rho } \sqrt{\log (D)}}{\sqrt{\theta }} \beta _0,\alpha _1=\pm \frac{\root 4 \of {-\frac{1}{2}} \sqrt{\lambda } \root 4 \of {\rho } \sqrt{\log (D)}}{\sqrt{\theta }} \beta _1,\omega =-\frac{ \sqrt{-2}}{\sqrt{\rho } \log (D)}\right\} , \end{aligned}$$
(32)

By using the Eqs. (32) and (31) into Eq. (2), we acquire

$$\begin{aligned} q(x, t )=\frac{ \root 4 \of {-\frac{1}{2}} \sqrt{\lambda } \root 4 \of {\rho } \sqrt{\log (D)}}{\sqrt{\theta }} \left( \frac{\mp \beta _0\pm \beta _1 D^{(\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }) }}{\beta _0+\beta _1 D^{(\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }) }}\right) , \end{aligned}$$
(33)
Fig. 10
figure 10

Graph of (\(Exp_a\) function method) Set 1, Case 1 \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5, -10<x<10, 0<t<2\)

Full size image
Fig. 11
figure 11

Graph of (\(Exp_a\) function method) Set 1, Case 1 \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5, -10<x<10, t=1\)

Full size image
Fig. 12
figure 12

Graph of (\(Exp_a\) function method) Set 1, Case 1 \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5,-10<x<10, 0<t<2\)

Full size image

Set 2:

$$\begin{aligned} \left\{ \alpha _0=\pm \frac{(\sqrt{\lambda }-\sqrt{-\lambda }) \root 4 \of {\rho } \sqrt{\log (D)}}{2^{3/4} \sqrt{\theta }} \beta _0,\alpha _1=\mp \frac{(\sqrt{\lambda }-\sqrt{-\lambda }) \root 4 \of {\rho } \sqrt{\log (D)}}{2^{3/4} \sqrt{\theta }} \beta _1,\omega =\frac{ \sqrt{-2}}{\sqrt{\rho } \log (D)}\right\} , \end{aligned}$$
(34)

The use of the Eqs. (34) and (31) into Eq. (2), we acquire

$$\begin{aligned} q(x, t )=\frac{(\sqrt{\lambda }-\sqrt{-\lambda }) \root 4 \of {\rho } \sqrt{\log (D)}}{2^{3/4} \sqrt{\theta }} \left( \frac{\pm \beta _0\mp \beta _1 D^{(\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })}}{\beta _0+\beta _1 D^{(\omega x - \frac{\lambda }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })}}\right) , \end{aligned}$$
(35)

3 Physical explanation

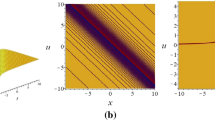
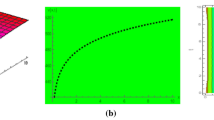
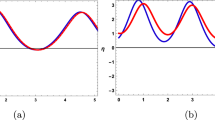
Here we present the physical significance of the above mentioned solutions to the beta-time fractional modified equal width equation. Plotting these solutions in 2-D at different time levels and different values of \(\beta\) and 3-D. We found interesting behaviors, depending on the values of the free constants in the gained solutions as shown in the figures. Figure 1; represents the dark soliton solution for the values \(\lambda =-0.3,\rho =1,\beta =1,\theta =2,B=0.5, -10<x<10, 0<t<2\) Figure 2; represents the dark soliton solution for the values \(\lambda =-0.3,\rho =1,t=1,\theta =2,B=0.5, -10<x<10\). Figure 3; represents the dark soliton solution for the values \(\lambda =-0.3,\rho =1,\theta =2, B=0.5, -10<x<10, 0<t<2\). Figure 4; represents the periodic soliton solution for the values \(\lambda =-0.2,\rho =1,\beta =1,\theta =2,B=0.5, -10<x<10, 0<t<2\). Figure 5; represents the periodic soliton solution for the values \(\lambda =-0.2,\rho =1,t=1,\theta =2,B=0.5, -10<x<10\). Figure 6; represents the periodic soliton solution for the values \(\lambda =-0.2,\rho =1,\theta =2,B=0.5, -10<x<10, 0<t<2\). Figure 7; represents the kink wave soliton solution for the values \(\lambda =-1, \rho =1.5, \beta =1, \theta =2, B=0.5,-10<x<10, 0<t<2\). Figure 8; represents the kink wave soliton solution for the values \(\lambda =-1, \rho =1.5, t=1, \theta =2, B=0.5, -10<x<10\). Figure 9; represents the kink wave soliton solution for the values \(\lambda =-1, \rho =1.5, \theta =2, B=0.5, -10<x<10, 0<t<2\). Figure 10; represents the rational wave solution for the values \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5, -10<x<10, 0<t<2\). Figure 11; represents the rational wave solution for the values \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5, -10<x<10, t=1\). Figure 12; represents the rational wave solution for the values \(\lambda =1.1,\rho =0.6,\beta _0=0.4,\beta _1=0.3,\theta =0.5,-10<x<10, 0<t<2\). The results of this work come with a lot of encouragement for further future discussion in different branches of science, especially in nonlinear optics and ocean engineering.

4 Results and discussion

Here we will compare the existing results and our obtained results of the concerned model. In Raslan et al. (2017), travelling wave solutions are obtained by using the modified extended tanh method. Kink solitons, periodic solitons and other soliton solutions of modified equal width equation with fractional derivative operator in the sense of Caputo are gained in Ali et al. (2022). Explicit and periodic solutions are obtained by applying extended simple equation and \(\exp (-\varphi (\xi ))\) methods in Lu et al. (2018). While we obtained the rational and other type of soliton solutions in the sense of beta-time derivative operator. Hence,our gained results are new and different from the existing results in the literature.

5 Conclusion

We have succussed to gain the singular and other type of soliton solutions of MEWE along BTD by applying the two different methods: \(\exp (-\phi (\eta ))\) and the \(Exp_a\) function methods. The acquired results are verified and also describe by figures. The first application of the BTD to this model is made in this study, and the results are crucial for the field’s continued advancement. The use of fractional derivative provides the more accurate results than the other. Impact of beta-time derivative is shown by graphically. The variable-order differential equation is a powerful mathematical model for describing difficult dynamical situations. Therefore, beta-time fractional derivative is used for the modified equal width equation so that the concerning model may be describe in a simple way.This research suggest that the used methods are simple, reliable and fruitful. As we all know, in the field of integrable systems, there is no general method to solve the Analytical solution of the nonlinear partial differential equation. The symbol calculation method based on neural networks proposed by Zhang et al. (2020, 2021b, 2022, 2023) open up a general symbolic computing path for the analytic solution of Nonlinear partial differential equation, and lays the foundation for the universal method of symbolic calculation of Analytical expression. The problems studied in this paper can be solved by using this method in the future work.