1 Introduction

Nonlinear evolution models are used to simulate a wide range of nonlinear processes that occur in nature, including computational science, engineering, mathematical physics (Sulaiman et al. 2020), applied mathematics, group dynamics, shallow water (Yusuf and Sulaiman 2021) and optics (Alquran et al. 2021; Sulaiman et al. 2021). Furthermore, it has been observed that when a system becomes unstable suddenly, the resulting dynamics are defined by the propagation of fronts in the population dynamics, combustions, mathematical ecology, chaos theory, turbulence, crystal growth, pulse propagation in nerves, and other areas (Panna and Islam 2013; Petrovskii et al. 2005). Different forms of wave propagations are represented by the precise solutions of nonlinear evolution models (Abdelrahman et al. 2015; Rached 2018, 2019). The study of traveling wave (TW) and solitary wave (SW) solutions has become an essential part of the mathematical analysis of nonlinear evolution equations in the following sections (Zhang and Zhang 2017; Roshid et al. 2020; Islam and Wang 2022). Solitary wave and soliton solutions, due to their inherent properties of maintaining their shape and velocity during propagation, offer a simpler analytical framework for analysis and examination (Kim et al. 2014; Kraenkel et al. 2013). Compared to alternative solutions, their stability nature contributes to their ease of handling in mathematical models and numerical simulations (Kumar et al. 2012; Polyanin and Sorokin 2021). Many mathematically modeled processes can utilize these solutions as comparison tools, aligning them with their social or natural occurrences (Singh et al. 2021; Yusuf 2020). Additionally, these solutions can be employed to define long-term behavior in various situations (Wazwaz 2012; Hu 2001; Hu and Zhang 2001). As a result of these, many techniques have been developed and used in the past two decades. Such as, the Jacobi elliptic function (Aslan and Inc 2017), the extended Fan sub-equation (Younis et al. 2020), Lie symmetry (Zhou et al. 2020; Hosseini et al. 2024), the simplified Hirota’s technique (Wazwaz( 2021), The Wentzel–Kramers–Brillouin asymptotic method (Sahu and Nirwal 2021), Darboux transformation (Raghuraman et al. 2021), the conformable sub-equation method (Yepez-Martinez and Gómez-Aguilar 2021), the improved system technique (Choi et al. 2019), the modified extended direct algebraic method (Seadawy et al. 2022), the linear superposition principle (Kuo and Ma 2022), tanh-sech method and modified Kudryashov method (Ray and Sahoo 2016; Kumar et al. 2020), the two variable \((G'/G, 1/G)\)-expansion (Huda et al. 2018; Bashar et al. 2022b), a variation of parameters method (VPM) and Adomian’s decomposition method (ADM) (Waheed et al. 2018), the invariant subspace scheme (Hosseini et al. 2020), q-homotopy analysis method and Sumudu transform (Dubey et al. 2021), modified versions of variational iteration algorithms (Ahmad et al. 2021), the standard B-spline collocation method (Kukreja et al. 2022), the generalized (Akbar et al. 2022) and new Kudryashov approaches (Rehman et al. 2024; Malik et al. 2023), generalized projective Riccati equation technique (Raza et al. 2020), sine-Gordon expansion scheme (Fahim et al. 2022), trial function technique (Chen et al. 2021), bifurcation analysis (Islam et al. 2024), (Arafat et al. 2023b), (Rayhanul 2023), stability analysis (Islam et al. 2023), the improved F-expansion scheme (Bashar et al. 2022a), the enhanced (\(G^\prime / G\))-expansion approach (Arafat et al. 2023a) and well-known many others.

Soliton solutions between nonlinear phenomena are widely known to have a variety of characteristics and soliton solutions. Throughout the last few decades, many researchers have studied soliton solutions as well as other types of integrable equations. Some nonintegrable equations have solutions as well. Furthermore, various studies have proved the existence of some solutions and other forms of exact solutions to nonlinear integrable equations. It’s worth noting, though, that a variety of methods have been employed to build interaction phenomena for nonlinear evolution models, particularly for equations with constant coefficients. In some circumstances, values are assigned to these constant coefficients to ensure that solutions exist. Nonetheless, it is clear that there is still a significant gap to be felt in this direction. So, studying numerous other equations with different features and forms is critical in order to develop many more physical qualities and features (Dey et al. 2024; Rasid et al. 2024). Inspired by this, we study with the application of the eMETEM (Ozisik et al. 2022) to the \((2+1)\)-DSE (Boateng et al. 2019) and the \((2+1)\)-CCMS (Pekcan 2021). The eMETEM offers several advantages compared to other analytical methods for solving nonlinear partial differential equations (NLPDEs). The eMETEM is a flexible approach that can be applied to a wide range of NLPDEs, including both integrable and non-integrable systems. This method is effective for the characterization and identification of various types of solitons like dark, bright, singular, periodic, and multi-soliton solutions. It provides a systematic approach to producing analytical solutions with efficiency. It is a method that is easy to implement and does not involve substantial computational complexity.

The well-known (\(2+1\))-DSE is defined as (Ebadi et al. 2011):

$$\begin{aligned}{} & {} i\frac{\partial \Theta }{\partial t} +a\left( \frac{\partial ^{2} \Theta }{\partial x^{2} } +\frac{\partial ^{2} \Theta }{\partial y^{2} } \right) +b\left| \Theta \right| ^{2} \Theta -\alpha \Theta \Phi =0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \frac{\partial ^{2} \Phi }{\partial x^{2} } +\frac{\partial ^{2} \Phi }{\partial y^{2} } -\beta \frac{\partial \left( \left| \Theta \right| ^{2} \right) }{\partial x^{2} } =0, \end{aligned}$$
(2)

in which a denotes the coefficient governing the spatial dispersion of the wave field in both x and y directions, b is the strength of the nonlinear self-interaction term parameter, and \(i=\sqrt{-1}\). Besides, \(\Theta (x,y,t)\), \(\Phi (x,y,t)\) represent the surface wave packet and the velocity potential of the mean flow interacting with the surface wave, respectively. Moreover, \(\alpha \) represents the coefficient of coupling between \(\Theta (x,y,t)\) and \(\Phi (x,y,t)\), determining the strength of the interaction between two components. Also, \(\beta \) represents the strength of the nonlinear coupling term parameter in Eq. (2).

This equation models the water waves in dual spatial directions with weak nonlinearity and it is an important equation for studying the evolution of water waves where the amplitude of the waves can be modulated in spatial directions and it has many applications. It is also used to describe the events of the 3-dimensional wave packet and long wave-short wave resonances at the finite depth water surface (Besse and Lannes 2001; Babaoglu 2008).

The \((2+1)\)-DSE equation has been the subject of some studies before. Variable-coefficient form in (El-Shiekh and Gaballah 2020) was considered and the novel SW solutions of the complex nonlinear DSE were acquired using the extended exponential function and the Khater II methods in (Khater and Salama 2021). Besides, new exact solutions and modulation instability were investigated via generalized elliptic equation rational expansion in (Boateng et al. 2019), and soliton solutions of the generalized DSE with the complex coefficients were produced with the help of the extended tanh-coth and modified simple equation method in (Jawad et al. 2018). Moreover, to study the \((2+1)\)-DSE, new extended generalized Kudryashov method (Zayed et al. 2020), Bäcklund transformation and Lax pair (Zhao et al. 2018), the mapping method (Ebadi et al. 2011) were implemented.

The \((2+1)\)-CCMS is defined as (Miah et al. 2020):

$$\begin{aligned}{} & {} i\frac{\partial \Psi }{\partial t} +\frac{\partial ^{2} \Psi }{\partial x^{2} } +\Psi \Gamma =0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \frac{\partial \Gamma }{\partial x} +\frac{\partial \Gamma }{\partial y} +\frac{\partial \left( \left| \Psi \right| ^{2} \right) }{\partial x} =0, \end{aligned}$$
(4)

where t is the temporal, x and y are the spatial variables, and \(i=\sqrt{-1}\). \(\Gamma (x,y,t)\) and \(\Psi (x,y,t)\) represent the real and complex scalar fields, respectively.The \((2+1)\)-CCMS is generally used to model the dynamics of isolated waves localized in a very small part of space. It has different usage fields, such as plasma physics, quantum mechanics, hydrodynamics, and Langmuir solitons in nonlinear optics. Besides, this equation can also be used to model oceans and gravity waves in a small part of the domain. The \((2+1)\)-CCMS has been investigated in different studies. Such abundant closed-form wave solutions for the \((2+1)\)-CCMS in (Miah et al. 2020) and new-fashioned solitons of coupled nonlinear Maccari systems in (Islam et al. 2022) were derived.Besides, nonlinear vibration motions of isolated waves localized in a small part of space were examined in (Wang and Khater 2022). Moreover, new exact soliton solutions to the nonlinear Maccari’s system (Bilal and Ahmad 2022), propagation of isolated waves of coupled nonlinear \((2+1)\)-CCMS (Cheemaa et al. 2020), new SW solutions of the Maccari system (Demiray et al. 2015), new exact solutions for the Maccari system (Abdelrahman and Hassan 2018) were retrieved. Furthermore, the singular bell-shaped, irregular periodic, and anti-bell-shaped solitons for \((2+1)\)-CCMS were produced in (Yiasir Arafat et al. 2023). Although numerical methods have been broadly utilized, there is a need for further improvement of analytical approaches to acquire analytical solutions. Analytical insights provide a deeper understanding of the underlying dynamics. While there have been studies in the literature focusing on finding analytical solutions for the \((2+1)\)-DSE and the \((2+1)\)-CCMS using several different approaches, this study marks the first time that the eMETEM has been applied to these two equations. The contribution of this study to the literature is significant in this regard. Additionally, another contribution of this study to the literature is the examination of the effects of parameters and the coupling coefficients of the \((2+1)\)-DSE on soliton behavior. Exploring different coupling mechanisms and their effects on soliton dynamics would provide insights into the underlying physics of the system. The rest of the body of the article is constructed as follows: The summary of the eMETEM is given in Sect. 2. Section 3 pertains to the implementation of the proposed method. Section 4 is devoted to results and discussion. Section 5, which is the last part, gives the conclusion.

2 The summary of the eMETEM

Step 1 Imagine the given NLPDE and the related transformations:

$$\begin{aligned}{} & {} F\left( \Theta ,\frac{\partial \Theta }{\partial t},\frac{\partial \Theta }{\partial x},\frac{\partial ^{2} \Theta }{\partial t^{2} },\frac{\partial ^{2} \Theta }{\partial x^{2} },\frac{\partial ^{2} \Theta }{\partial x\partial t},\Theta ^{2} \frac{\partial ^{2} \Theta }{\partial x^{2} },...\right) =0, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \Theta \left( x,y,t\right) =\Theta \left( \zeta \right) , \quad \zeta =x+y+\beta t. \end{aligned}$$
(6)

Insertion of Eq. (6) into Eq. (5), gives the nonlinear ordinary differential equation (NODE):

$$\begin{aligned} P\left( \Theta \left( \zeta \right) ,\Theta '\left( \zeta \right) ,\Theta ''\left( \zeta \right) ,\Theta ^{2} \left( \zeta \right) \Theta '\left( \zeta \right) ,...\right) =0. \end{aligned}$$
(7)

In Eq. (7), P is a polynomial in \(\Omega \left( \zeta \right) \) and the \('=\frac{d}{d \zeta }\).

Step2 The solution of Eq. (7) is proposed in the following structure:

$$\begin{aligned} \Theta \left( \zeta \right) =f_{0} +\sum _{i=-m}^{m}f_{i} \Omega ^{i}(\zeta ). \end{aligned}$$
(8)

In Eq. (8), \(f_{-m},...,f_{0},...,f_{m}\) are real values to be calculated, and \(f_{-m},f_{m}\) should not be zero simultaneously. With the aid of the balancing rule in Eq. (7), one can calculate the m which is a positive integer and called the balancing constant. Besides, the \(\Omega (\zeta )\) satisfies the following formula:

$$\begin{aligned} \frac{d\Omega (\zeta )}{d\zeta } =w +\left[ \Omega (\zeta )\right] ^{2}, \end{aligned}$$
(9)

where w is a non-zero real number.

Step3 \(\Omega (\zeta )\) in Eq. (9) admits the following solutions given by Table 1 (Ozisik et al. 2022).

Table 1 The solutions of Eq. (9)
Full size table

Step4 Substituting Eqs. (8) and (9) into Eq. (7) gives a polynomial in various powers of \(\Omega (\zeta )\). Collecting the \(\Omega (\zeta )\) in the same power and setting each term to zero, we derive an algebraic equation system for \(f_{-m},...,f_0,...,f_m, w\) and \(\beta \).

Step5 The solution of the algebraic equation form in Step 4 produces many suitable solution sets. Combination of selected suitable solution sets, Eqs. (6), (8), and Table 1 gives the solution of NLPDE in Eq. (5).

3 Implementation of the eMETEM

3.1 Application to the \((2+1)\)-DSE

Imagine the DSE given in Eqs. (1) and (2) then insert the following complex transformation:

$$\begin{aligned} \Theta (x,y,t)= \Theta (\zeta )e^{i\theta }, \quad \phi (x,y,t)=\phi (\zeta ), \quad \zeta =x+y+ct, \quad \theta =\sigma x+py+rt, \end{aligned}$$
(10)

where \(\theta \) is the phase component described as a linear combination of spatial coordinates x and y with real parameters \(\sigma ,p,r\) to be determined. Besides, c is a constant representing the speed of propagation. Substitution of Eq. (10) into Eqs. (1) and (2) produces the following equations:

$$\begin{aligned}{} & {} 2\left( \frac{\textrm{d}^{2} \Theta \left( \zeta \right) }{\textrm{d}\zeta ^{2} } \right) a+i \left( 2a \left( p+\sigma \right) +c\right) \frac{\mathrm{d \Theta \left( \zeta \right) }}{\textrm{d}\zeta } -\left( \begin{array}{l} {-b\left( \Theta \left( \zeta \right) \right) ^{2} } +\alpha \Phi \left( \zeta \right) \\ +\left( p^{2} +\sigma ^{2} \right) a+r \end{array}\right) \Theta \left( \zeta \right) =0, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} 2\beta \left( \left( \frac{\mathrm{d \Theta \left( \zeta \right) }}{\textrm{d }\zeta } \right) ^{2} +\Theta \left( \zeta \right) \frac{\textrm{d}^{2} \Theta \left( \zeta \right) }{\textrm{d}\zeta ^{2} } \right) +2\frac{\textrm{d}^{2} \Phi \left( \zeta \right) }{\textrm{d}\zeta ^{2} } =0. \end{aligned}$$
(12)

Organizing the real and imaginary parts of Eq. (11), the following equations are gained:

$$\begin{aligned}{} & {} 2\left( \frac{\textrm{d}^{2} \Theta \left( \zeta \right) }{\textrm{d}\zeta ^{2} } \right) a-\Theta \left( \zeta \right) \left( -b\left( \Theta \left( \zeta \right) \right) ^{2} +\alpha \Phi \left( \zeta \right) +\left( p^{2} +\sigma ^{2} \right) a+r\right) =0, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \left( \left( 2p+2\sigma \right) a+c\right) \frac{\mathrm{d \Theta \left( \zeta \right) }}{\textrm{d}\zeta } =0. \end{aligned}$$
(14)

Eq. (14) yields,

$$\begin{aligned} c=-2a\left( \sigma +p\right) . \end{aligned}$$
(15)

Taking the integral constants to zero and integrating the Eq. (12) twice gives Eq. (16).

$$\begin{aligned} \Phi (\zeta )=-\frac{\beta \left( \Theta \left( \zeta \right) \right) ^{2} }{2}. \end{aligned}$$
(16)

Substituting the Eq. (16) into Eq. (11) we get the NODE form of the Eq. (1).

$$\begin{aligned} \left( \alpha \beta +2b\right) \left( \Theta \left( \zeta \right) \right) ^{3} -2\left( r+a\left( p^{2} +\sigma ^{2} \right) \right) \Theta \left( \zeta \right) +4a\frac{\textrm{d}^{2} }{\textrm{d}\zeta ^{2} } \Theta \left( \zeta \right) =0. \end{aligned}$$
(17)

Taking into account the terms \(\Theta ''(\zeta )\) and \(\Theta ^{3} (\zeta ) \) in Eq. (17), result is \(m=1\). So, one can write the Eq. (8) in the following form:

$$\begin{aligned} \Theta (\zeta )=a_{0} +a_{1} \Omega (\zeta )+b_{1} \frac{1}{\Omega (\zeta )}. \end{aligned}$$
(18)

Inserting the Eqs. (18) and (9) into Eq. (17), we reach the polynomial form of \(\Omega (\zeta )\) which involves different powers of \(\Omega (\zeta )\). The solution of this form requires that each coefficient of \(\Omega ^{i}(\zeta )\) should be zero. Then we derive the following over-determined algebraic system:

$$\begin{aligned} \begin{aligned}&\Omega ^{-3} (\zeta ):\left( \alpha \beta +2b\right) b_{1} {}^{3} +8aw^{2} b_{1} =0, \\&\Omega ^{-2} (\zeta ):6a_{0} \left( 1/2\beta \alpha +b\right) b_{1} {}^{2} =0, \\&\Omega ^{-1} (\zeta ):-2b_{1} \left( -3\left( 1/2\beta \alpha +b\right) a_{1} b_{1} +\left( p^{2} +\sigma ^{2} -4w\right) a+\left( -3/2\beta \alpha -3b\right) a_{0} {}^{2} +r\right) =0, \\&\Omega ^{0} (\zeta ):-2a_{0} \left( \left( -1/2\beta \alpha -b\right) a_{0} {}^{2} -6\left( 1/2\beta \alpha +b\right) a_{1} b_{1} +a\left( p^{2} +\sigma ^{2} \right) +r\right) =0, \\&\Omega ^{1} (\zeta ):-2\left( -3\left( 1/2\beta \alpha +b\right) a_{1} b_{1} +\left( p^{2} +\sigma ^{2} -4w\right) a+\left( -3/2\beta \alpha -3b\right) a_{0} {}^{2} +r\right) a_{1} =0, \\&\Omega ^{2} (\zeta ):6a_{0} \left( 1/2\beta \alpha +b\right) a_{1} {}^{2} =0, \\&\Omega ^{3} (\zeta ):\left( \beta \alpha +2b\right) a_{1} {}^{3} +8a a_{1} =0. \end{aligned} \end{aligned}$$
(19)

One of the sets obtained by solving this system is as follows:

$$\begin{aligned} Dset=\left\{ \begin{array}{l} {r=-\frac{12a w \alpha \beta }{\Delta }-ap^2-a \sigma ^2 - \frac{24 a w b}{\Delta }+4 a w, a_0=0, a_1=2 \frac{\sqrt{-2 a \Delta }}{\Delta }, b_1=2\frac{\sqrt{-2 a \Delta } w}{\Delta }} \end{array}\right\} , \end{aligned}$$
(20)

where \(\Delta = \alpha \beta + 2b\). Taking into account the Eqs. (10), (16), and (18) in Table 1, we can write the solution functions of Eqs. (1) and (2) in the following general forms:

$$\begin{aligned} \Theta _1 (x,y,t)= & {} \left( a_0 -a_1 \sqrt{-w} \tanh (\sqrt{-w}\zeta ) - b_1 \frac{1}{\sqrt{-w} \tanh (\sqrt{-w}\zeta )} \right) e^{i\theta }, \nonumber \\ \Phi _1 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _1 (\zeta ) \right) ^2, \end{aligned}$$
(21)
$$\begin{aligned} \Theta _2 (x,y,t)= & {} \left( a_0 -a_1 \sqrt{-w} \coth (\sqrt{-w}\zeta ) - b_1 \frac{1}{\sqrt{-w} \coth (\sqrt{-w}\zeta )} \right) e^{i\theta }, \nonumber \\ \Phi _2 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _2 (\zeta ) \right) ^2, \end{aligned}$$
(22)
$$\begin{aligned} \Theta _3(x,y,t)= & {} \left( \begin{array}{l} {a_0-a_1 \sqrt{-w} \left( \tanh (2 \sqrt{-w}\zeta )+i \varepsilon sech (2\sqrt{-w}\zeta ) \right) } \\ - \frac{b_1}{\sqrt{-w} \left( \tanh (2\sqrt{-w}\zeta ) +i sech (2\sqrt{-w}\zeta ) \right) } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _3 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _3 (\zeta ) \right) ^2, \end{aligned}$$
(23)
$$\begin{aligned} \Theta _4(x,y,t)= & {} \left( a_0 + a_1 \frac{w-\sqrt{-w} \tanh (\sqrt{-w}\zeta )}{1+\sqrt{-w}\tanh (\sqrt{-w}\zeta } + b_1 \frac{1+\sqrt{-w}\tanh (\sqrt{-w}\zeta )}{w-\sqrt{-w}\tanh (\sqrt{-w}\zeta )} \right) e^{i\theta }, \nonumber \\ \Phi _4 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _4 (\zeta ) \right) ^2, \end{aligned}$$
(24)
$$\begin{aligned} \Theta _5(x,y,t)= & {} \left( a_0 + a_1 \sqrt{-w} \frac{5- 4 \cosh (2\sqrt{-w}\zeta )}{3+4 \sinh (2\sqrt{-w}\zeta )} + b_1 \frac{3+4 \sinh (2\sqrt{-w}\zeta )}{\sqrt{-w}\left( 5-4\cosh (2\sqrt{-w}\zeta ) \right) } \right) e^{i\theta }, \nonumber \\ \Phi _5 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _5 (\zeta ) \right) ^2, \end{aligned}$$
(25)
$$\begin{aligned} \Theta _6(x,y,t)= & {} \left( \begin{array}{l} {a_0+a_1 \frac{\epsilon \sqrt{-(D^2+E^2)w} - D\sqrt{-w}\cosh (2\sqrt{-w}\zeta )}{D \sinh (2\sqrt{-w}\zeta )+E} }\\ +b_1 \frac{D \sinh (2\sqrt{-w}\zeta )+E}{\epsilon \sqrt{-(D^2+E^2)w} -D\sqrt{-w}\cosh (2\sqrt{-w}\zeta ) } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _6 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _6 (\zeta ) \right) ^2, \end{aligned}$$
(26)
$$\begin{aligned} \Theta _7(x,y,t)= & {} \left( \begin{array}{l} {a_0+a_1 \left( \epsilon \sqrt{-w}-2 \frac{\epsilon D \sqrt{-w}}{D+ \cosh (2\sqrt{-w}\zeta )-\epsilon \sinh (2\sqrt{-w}\zeta )} \right) }\\ + \frac{b_1}{\epsilon \sqrt{-w}- \frac{\epsilon 2D \sqrt{-w}}{D+\cosh (2\sqrt{-w}\zeta )-\epsilon \sinh (2\sqrt{-w}\zeta )} } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _7 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _7 (\zeta ) \right) ^2, \end{aligned}$$
(27)
$$\begin{aligned} \Theta _8 (x,y,t)= & {} \left( a_0 +a_1 \sqrt{w} \tan (\sqrt{w}\zeta ) + \frac{b_1}{\sqrt{w} \tan (\sqrt{w}\zeta )} \right) e^{i\theta }, \nonumber \\ \Phi _8 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _8 (\zeta ) \right) ^2, \end{aligned}$$
(28)
$$\begin{aligned} \Theta _9 (x,y,t)= & {} \left( a_0 -a_1 \sqrt{w} \cot (\sqrt{w}\zeta ) - \frac{b_1}{\sqrt{w} \cot (\sqrt{w}\zeta )} \right) e^{i\theta }, \nonumber \\ \Phi _9 (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _9 (\zeta ) \right) ^2, \end{aligned}$$
(29)
$$\begin{aligned} \Theta _{10} (x,y,t)= & {} \left( \begin{array}{l} {a_0 +a_1 \sqrt{w} \left( \tan (2\sqrt{w}\zeta )+\epsilon \sec (2\sqrt{w}\zeta ) \right) } \\ + \frac{b_1}{\sqrt{w} \left( \tan (2\sqrt{w}\zeta ) +\epsilon \sec (2\sqrt{w}\zeta ) \right) } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _{10} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{10} (\zeta ) \right) ^2, \end{aligned}$$
(30)
$$\begin{aligned} \Theta _{11}(x,y,t)= & {} \left( a_0 - a_1 \sqrt{w} \frac{1- \tan (\sqrt{w}\zeta )}{1+\tan (\sqrt{w}\zeta )} - b_1 \frac{1+\tan (\sqrt{w}\zeta )}{\sqrt{w} \left( 1- \tan (\sqrt{w}\zeta ) \right) } \right) e^{i\theta },\nonumber \\ \Phi _{11} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{11} (\zeta ) \right) ^2, \end{aligned}$$
(31)
$$\begin{aligned} \Theta _{12}(x,y,t)= & {} \left( a_0 + a_1 \sqrt{w} \frac{4- 5 \cos (2\sqrt{w}\zeta )}{3+5 \sin (2\sqrt{w}\zeta )} + b_1 \frac{3+5 \sin (2\sqrt{w}\zeta )}{\sqrt{w}\left( 4-5\cos (2\sqrt{w}\zeta ) \right) } \right) e^{i\theta }, \nonumber \\ \Phi _{12} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{12} (\zeta ) \right) ^2, \end{aligned}$$
(32)
$$\begin{aligned} \Theta _{13}(x,y,t)= & {} \left( \begin{array}{l} {a_0+a_1 \frac{\epsilon \sqrt{(D^2-E^2)w} - D\sqrt{w}\cos (2\sqrt{w}\zeta )}{D \sin (2\sqrt{w}\zeta )+E} }\\ +b_1 \frac{D \sin (2\sqrt{w}\zeta )+E}{\epsilon \sqrt{(D^2-E^2)w} -D\sqrt{w}\cos (2\sqrt{w}\zeta ) } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _{13} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{13} (\zeta ) \right) ^2, \end{aligned}$$
(33)
$$\begin{aligned} \Theta _{14}(x,y,t)= & {} \left( \begin{array}{l} {a_0+a_1 \left( i \epsilon \sqrt{w}- \frac{2 i \epsilon D \sqrt{w}}{D+ \cos (2\sqrt{w}\zeta )-i \epsilon \sin (2\sqrt{w}\zeta )} \right) }\\ + \frac{b_1}{i \epsilon \sqrt{w}- \frac{2i \epsilon D \sqrt{w}}{D+\cos (2\sqrt{w}\zeta )-i \epsilon \sin (2\sqrt{w}\zeta )} } \end{array} \right) e^{i\theta }, \nonumber \\ \Phi _{14} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{14} (\zeta ) \right) ^2, \end{aligned}$$
(34)
$$\begin{aligned} \Theta _{15}(x,y,t)= & {} -\frac{1}{\zeta }, \nonumber \\ \Phi _{15} (x,y,t)= & {} -\frac{\beta }{2} \left( \Theta _{15} (\zeta ) \right) ^2, \end{aligned}$$
(35)

where \(\theta =py+rt+\sigma x\) and \(\zeta =x+y+c t\) as in given by Eq. (10).

3.2 Application to the \((2+1)\)-CCMS

Let consider the \((2+1)\)-CCMS given in Eqs. (3) and (4). Applying the complex transformation

$$\begin{aligned} \Psi (x,y,t)= \Psi (\zeta ) e^{i\theta }, \quad \Gamma (x,y,t)=\Gamma (\zeta ), \quad \zeta =x+y+ct, \quad \theta =ax+by+rt, \end{aligned}$$
(36)

gives the following equations:

$$\begin{aligned}{} & {} \frac{\textrm{d}^{2} \Psi \left( \zeta \right) }{\textrm{d}\zeta ^{2} } +i \left( 2a+c\right) \frac{\textrm{d }\Psi \left( \zeta \right) }{\textrm{d}\zeta } +\left( -a^{2} -r+\Gamma \left( \zeta \right) \right) \Psi \left( \zeta \right) =0, \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \left( c+1\right) \frac{\textrm{d}\Gamma \left( \zeta \right) }{\textrm{d}\zeta } + 2\Psi \left( \zeta \right) \frac{\textrm{d} \Psi \left( \zeta \right) }{\textrm{d}\zeta } =0. \end{aligned}$$
(38)

By separating the Eq. (37) into two components, which are real and imaginary, we derive:

$$\begin{aligned}{} & {} \frac{\textrm{d}^{2} }{\textrm{d}\zeta ^{2} } \Psi \left( \zeta \right) +\left( -a^{2} -r+\Gamma \left( \zeta \right) \right) \Psi \left( \zeta \right) =0, \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \left( 2a+c\right) \frac{\mathrm{d \Psi \left( \zeta \right) }}{\textrm{d}\zeta } =0. \end{aligned}$$
(40)

The result of Eq. (40) is

$$\begin{aligned} c=-2a. \end{aligned}$$
(41)

Integrating the Eq. (38) with respect to \(\zeta \) once and accepting the integration constant to zero gives the following formula:

$$\begin{aligned} \Gamma (\zeta )=-\frac{\left( \Psi \left( \zeta \right) \right) ^{2} }{c+1}. \end{aligned}$$
(42)

Inserting the Eq. (42) into Eq. (39), we obtain the NODE form of the Eq. (3):

$$\begin{aligned} \left( \Psi \left( \zeta \right) \right) ^{3} +\left( a^{2} +r\right) \left( 1-2a\right) \Psi \left( \left( \zeta \right) \right) +\left( 2a-1\right) \frac{\textrm{d}^{2} \Psi \left( \zeta \right) }{\textrm{d}\left( \zeta \right) ^{2} } =0. \end{aligned}$$
(43)

We reach \(m=1\) with the aid of the homogeneous balance rule between \(\Psi ''(\zeta )\) and \(\Psi ^{3}(\zeta )\) in Eq. (43). Insertion of the Eqs. (18) and (9) into Eq. (43) produces a polynomial form of the \(\Omega (\zeta )\). Organizing the \(\Omega ^{i} (\zeta )\) with respect to various powers of \(\Omega (\zeta )\), we have an algebraic equation system as follows:

$$\begin{aligned} \begin{aligned}&\Omega ^{-3} (\zeta ):b_{1}^{3} +4w^{2} \left( a-1/2\right) b_{1} =0, \\&\Omega ^{-2} (\zeta ):3a_{0} b_{1} {}^{2} =0, \\&\Omega ^{-1} (\zeta ):-2b_{1} \left( a^{3} -1/2a^{2} +\left( r-2w\right) a-3/2a_{0} {}^{2} -3/2a_{1} b_{1} -r/2+w\right) =0, \\&\Omega ^{0} (\zeta ):-a_{0} \left( 2a^{3} -a^{2} +2ar-a_{0} {}^{2} -6a_{1} b_{1} -r\right) =0, \\&\Omega ^{1} (\zeta ):-2\left( a^{3} -1/2a^{2} +\left( r-2w\right) a-3/2a_{0} {}^{2} -3/2a_{1} b_{1} -r/2+w\right) a_{1} =0, \\&\Omega ^{2} (\zeta ):3a_{0} a_{1} {}^{2} =0, \\&\Omega ^{3} (\zeta ):a_{1} \left( a_{1} {}^{2} +4a-2\right) =0. \end{aligned} \end{aligned}$$
(44)

The solution of the above system serves the following sets:

$$\begin{aligned} \begin{aligned} Mset1&=\left\{ r=\frac{2(2-4a)w-2a^3 + a^2}{2a-1}, a_0=0, a_1=\sqrt{2-4a}, b_1=\sqrt{2-4a}w \right\} , \\ Mset2&=\left\{ a=-\sqrt{-r+2w}, a_0=0, a_1=\sqrt{2+4 \sqrt{-r+2w}}, b_1=0 \right\} . \end{aligned} \end{aligned}$$
(45)

Taking into account the Eqs. (18), (36), (41) and (42) in Table 1, we can write the solutions functions of Eqs. (3) and (4) in the following general forms as in the previous investigated problem.

$$\begin{aligned} \Psi _1 (x,y,t)= & {} \, \left( a_0 -a_1 \sqrt{-w} \tanh (\sqrt{-w}\zeta ) - b_1 \frac{1}{\sqrt{-w} \tanh (\sqrt{-w}\zeta )} \right) e^{i \theta }, \nonumber \\ \Gamma _1 (x,y,t)= & {} -\frac{1}{c+1} \left( \Psi _1 (\zeta ) \right) ^2, \end{aligned}$$
(46)
$$\begin{aligned} \Psi _2 (x,y,t)= & {}\, \left( a_0 -a_1 \sqrt{-w} \coth (\sqrt{-w}\zeta ) - b_1 \frac{1}{\sqrt{-w} \coth (\sqrt{-w}\zeta )} \right) e^{i \theta }, \nonumber \\ \Gamma _2 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _2 (\zeta ) \right) ^2, \end{aligned}$$
(47)
$$\begin{aligned} \Psi _3(x,y,t)= & {} \, \left( \begin{array}{l} {a_0-a_1 \sqrt{-w} \left( \tanh (2 \sqrt{-w}\zeta )+i \varepsilon sech (2\sqrt{-w}\zeta ) \right) } \\ - \frac{b_1}{\sqrt{-w} \left( \tanh (2\sqrt{-w}\zeta ) +i sech (2\sqrt{-w}\zeta ) \right) } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _3 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _3 (\zeta ) \right) ^2, \end{aligned}$$
(48)
$$\begin{aligned} \Psi _4(x,y,t)= & {} \, \left( a_0 + a_1 \frac{w-\sqrt{-w} \tanh (\sqrt{-w}\zeta )}{1+\sqrt{-w}\tanh (\sqrt{-w}\zeta )} + b_1 \frac{1+\sqrt{-w}\tanh (\sqrt{-w}\zeta )}{w-\sqrt{-w}\tanh (\sqrt{-w}\zeta )} \right) e^{i \theta }, \nonumber \\ \Gamma _4 (x,y,t)= & {} \, - \frac{1}{c+1} \left( \Psi _4 (\zeta ) \right) ^2, \end{aligned}$$
(49)
$$\begin{aligned} \Psi _5(x,y,t)= & {} \, \left( a_0 + a_1 \sqrt{-w} \frac{5- 4 \cosh (2\sqrt{-w}\zeta )}{3+4 \sinh (2\sqrt{-w}\zeta )} + b_1 \frac{3+4 \sinh (2\sqrt{-w}\zeta )}{\sqrt{-w}\left( 5-4\cosh (2\sqrt{-w}\zeta ) \right) } \right) e^{i \theta }, \nonumber \\ \Gamma _5 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _5 (\zeta ) \right) ^2, \end{aligned}$$
(50)
$$\begin{aligned} \Psi _6(x,y,t)= & {} \, \left( \begin{array}{l} {a_0+a_1 \frac{\epsilon \sqrt{-(D^2+E^2)w} - D\sqrt{-w}\cosh (2\sqrt{-w}\zeta )}{D \sinh (2\sqrt{-w}\zeta )+E} }\\ +b_1 \frac{D \sinh (2\sqrt{-w}\zeta )+E}{\epsilon \sqrt{-(D^2+E^2)w} -D\sqrt{-w}\cosh (2\sqrt{-w}\zeta ) } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _6 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _6 (\zeta ) \right) ^2, \end{aligned}$$
(51)
$$\begin{aligned} \Psi _7(x,y,t)= & {} \, \left( \begin{array}{l} {a_0+a_1 \left( \epsilon \sqrt{-w}-2 \frac{\epsilon D \sqrt{-w}}{D+ \cosh (2\sqrt{-w}\zeta )-\epsilon \sinh (2\sqrt{-w}\zeta )} \right) }\\ + \frac{b_1}{\epsilon \sqrt{-w}- \frac{\epsilon 2D \sqrt{-w}}{D+\cosh (2\sqrt{-w}\zeta )-\epsilon \sinh (2\sqrt{-w}\zeta )} } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _7 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _7 (\zeta ) \right) ^2, \end{aligned}$$
(52)
$$\begin{aligned} \Psi _8 (x,y,t)= & {} \, \left( a_0 +a_1 \sqrt{w} \tan (\sqrt{w}\zeta ) + \frac{b_1}{\sqrt{w} \tan (\sqrt{w}\zeta )} \right) e^{i \theta }, \nonumber \\ \Gamma _8 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _8 (\zeta ) \right) ^2, \end{aligned}$$
(53)
$$\begin{aligned} \Psi _9 (x,y,t)= & {} \, \left( a_0 -a_1 \sqrt{w} \cot (\sqrt{w}\zeta ) - \frac{b_1}{\sqrt{w} \cot (\sqrt{w}\zeta )} \right) e^{i \theta }, \nonumber \\ \Gamma _9 (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _9 (\zeta ) \right) ^2, \end{aligned}$$
(54)
$$\begin{aligned} \Psi _{10} (x,y,t)= & {} \, \left( \begin{array}{l} {a_0 +a_1 \sqrt{w} \left( \tan (2\sqrt{w}\zeta )+\epsilon \sec (2\sqrt{w}\zeta ) \right) } \\ + \frac{b_1}{\sqrt{w} \left( \tan (2\sqrt{w}\zeta ) +\epsilon \sec (2\sqrt{w}\zeta ) \right) } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _{10} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{10} (\zeta ) \right) ^2, \end{aligned}$$
(55)
$$\begin{aligned} \Psi _{11}(x,y,t)= & {} \, \left( a_0 - a_1 \sqrt{w} \frac{1- \tan (\sqrt{w}\zeta )}{1+\tan (\sqrt{w}\zeta )} - b_1 \frac{1+\tan (\sqrt{w}\zeta )}{\sqrt{w} \left( 1- \tan (\sqrt{w}\zeta ) \right) } \right) e^{i \theta }, \nonumber \\ \Gamma _{11} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{11} (\zeta ) \right) ^2, \end{aligned}$$
(56)
$$\begin{aligned} \Psi _{12}(x,y,t)= & {} \, \left( a_0 + a_1 \sqrt{w} \frac{4- 5 \cos (2\sqrt{w}\zeta )}{3+5 \sin (2\sqrt{w}\zeta )} + b_1 \frac{3+5 \sin (2\sqrt{w}\zeta )}{\sqrt{w}\left( 4-5\cos (2\sqrt{w}\zeta ) \right) } \right) e^{i \theta }, \nonumber \\ \Gamma _{12} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{12} (\zeta ) \right) ^2, \end{aligned}$$
(57)
$$\begin{aligned} \Psi _{13}(x,y,t)= & {} \, \left( \begin{array}{l} {a_0+a_1 \frac{\epsilon \sqrt{(D^2-E^2)w} - D\sqrt{w}\cos (2\sqrt{w}\zeta )}{D \sin (2\sqrt{w}\zeta )+E} }\\ +b_1 \frac{D \sin (2\sqrt{w}\zeta )+E}{\epsilon \sqrt{(D^2-E^2)w} -D\sqrt{w}\cos (2\sqrt{w}\zeta ) } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _{13} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{13} (\zeta ) \right) ^2, \end{aligned}$$
(58)
$$\begin{aligned} \Psi _{14}(x,y,t)= & {} \, \left( \begin{array}{l} {a_0+a_1 \left( i \epsilon \sqrt{w}- \frac{2 i \epsilon D \sqrt{w}}{D+ \cos (2\sqrt{w}\zeta )-i \epsilon \sin (2\sqrt{w}\zeta )} \right) }\\ + \frac{b_1}{i \epsilon \sqrt{w}- \frac{2i \epsilon D \sqrt{w}}{D+\cos (2\sqrt{w}\zeta )-i \epsilon \sin (2\sqrt{w}\zeta )} } \end{array} \right) e^{i \theta }, \nonumber \\ \Gamma _{14} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{14} (\zeta ) \right) ^2, \end{aligned}$$
(59)
$$\begin{aligned} \Psi _{15}(x,y,t)= & {} \, -\frac{1}{\zeta }, \nonumber \\ \Gamma _{15} (x,y,t)= & {} \, -\frac{1}{c+1} \left( \Psi _{15} (\zeta ) \right) ^2, \end{aligned}$$
(60)

where \(\zeta =x+y+ct\) and \(\theta =ax+by+rt\) as in given by Eq. (36).

4 Result and discussion

In this section, some graphical presentations of the \((2+1)\)-DSE and \((2+1)\)-CCMS are given. The graphical illustrations are represented for some of the obtained solutions given by Eqs. (21)–(35) for DSE and Eqs. (46)–(60) for CCME. While Fig. 1, 2, 3, 4, and 5 belong to the \((2+1)\)-DSE, Figs. 6, 7, and 8 are related to the \((2+1)\)-CCME.

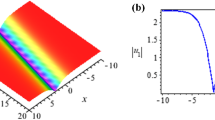
In Fig. 1, the graph of solution functions \(\Theta _3(x,y,t)\) and \(\Phi _3(x,y,t)\) in Eq. (23) is depicted by considering parameter values \(w=-0.1, a=0.75, b=-0.82, p=0.25, \sigma =0.65, \alpha =0.5, \beta =0.75\) and Dset given in Eq. (20). Figure 1a represents the 3D graph of the obtained solutions of \(|\Theta _3(x,y,t)|\) for \(t=1\), Fig. 1b illustrates the 3D plot of Im\((\Theta _3(x,y,t))\) for \(t=1\) and Fig. 1c depicts the 2D graphs of the \(|\Theta _3(x,1,t_f)|\) and Im\((\Theta _3(x,1,1))\). Here, \(t_f=1,2,3\) indicates the selected constant time. The bright soliton that has the traveling wave property is seen in Fig. 1a and c for \(|\Theta _3(x,y,1)|.\) Fig. 1d and e show the 3D and 2D graphs of \(\Phi _3(x,y,t)\) for t=1, respectively. These plots also demonstrate the bright soliton, which has a traveling wave property.

Fig. 1
figure 1

Some graphical presentations of \(\Theta _{3}(x,y,t)\) and \(\Phi _{3}(x,y,t)\) given by Eq. (23) for \(w=-0.1, \, a=0.75, \, b=-0.82, \, p=0.25, \, \sigma =0.65, \, \alpha =0.5, \, \beta =0.75\) with Dset in Eq. (20)

Full size image

Figure 2 is plotted to show the effect of the parameters \(a,\, b,\) and coupling parameters \(\alpha \) and \(\beta \) on the behavior of the soliton, which is obtained in Fig. 1a. The following graphs are depicted for the solution function \(\Theta _{3}(x,y,t)\) given by Eq. (23) by choosing parameters \(w=-0.1, \, p=0.25, \, \sigma =0.65\) with Dset in Eq. (20). In Fig. 2a, the graphs are represented considering \(b=-0.82, \, \alpha =0.5, \, \beta =1\) and selecting \(a=-2.00, \, -1.00, \, -0.75, \, -0.50, \, -0.15\) (color solid lines) and \(a=0.15, \, 0.50, \, 0.75, \, 1.00, \, 2.00\) (color dashed lines). When Fig. 2a is examined in detail, if \(\beta =1\), in case the parameter a is less than zero and increasing, the skirts of the soliton remain on the horizontal axis, the soliton both moves to the right on the horizontal axis, and the position of the top of the soliton changes vertically, in other words, the vertical amplitude of the soliton (height) decreases. When the parameter a is positive and increasing, the soliton moves to the right on the horizontal axis in the same way, and the peak amplitude (height) of the soliton changes to increase. Thus, the opposite sign of the parameter a has an inverse effect on the amplitude of the soliton.

The same examination is analyzed for \(\beta =-1\) in Fig. 2b. Although the same effects are observed as in Fig. 2a, the amount of change in vertical amplitude in Fig. 2b remains smaller than in Fig. 2a. For example, the maximum amplitude is greater than 2 in Fig. 2a while the maximum amplitude is less than 2 in Fig. 2b.

In Fig. 2c, since the graphs represented in Fig. 2a and b are categorically the same, it is examined whether the parameter \(\beta \) has any effect when \(\beta =1\) for Fig. 2a and \(\beta =-1\) for Fig. 2b. For this purpose, only positive values of \(0.15, \, 0.50, \, 0.75, \, 1.00\), and 2.00 are given to parameter a. Figure 2c illustrates the graphs for \(\beta =-1\) (color solid lines) and \(\beta =1\) (color dashed lines). It can be seen from Fig. 2c that if the parameter \(\beta \) takes the same absolute but opposite sign values, the amplitude of the soliton at positive \(\beta \) values is larger than the amplitude of the soliton at negative \(\beta \) values.

In Fig. 2d–f, the same analysis as in Fig. 2a, applying the balance principle Fig. 2c is studied for parameter b. It can be observed from Fig. 2d that there is no change in the position of the soliton horizontally, but the position of the soliton’s apex changes if \(\beta =1\) is a constant and parameter b takes the negative but increasing values. That is, the vertical amplitude (height) of the soliton changes. This change arises as an increase in the soliton’s amplitude when b is increasing and \(b<0\). However, the amplitude of the soliton decreases when b is increasing and \(b>0\). In Fig. 2e, when \(\beta =-1\) and the parameter b takes less than zero but increasing values, the same effect is observed as in Fig. 2d, that is, the soliton’s amplitude increases. The amplitude of the soliton decreases if b is greater than zero and increasing. Figure 2f is represented since the effect of the \(\beta \) parameter can not be examined from Fig. 2d and e exactly. In Fig. 2f, the graphs for \(\beta =-1\) (color solid lines) and \(\beta =1\) (color dashed lines) are depicted by giving only positive values to the parameter b. From Fig. 2f, it is seen that when the \(\beta \) parameter is negative, its effect on the soliton’s amplitude is increased compared to the case when it is positive. Figure 2g–2i show the analysis for the nonlinear coupling parameter \(\alpha \) when \(\beta =1\). In Fig. 2g, when \(\alpha \) is less than zero and increasing, the soliton does not change its position on the horizontal axis, but the vertical amplitude of the soliton changes. This change occurs as an increase in the cases of both \(\alpha <0\) and \(\alpha >0\) is increasing.

Figure 2h demonstrates the effect of the parameter \(\alpha \) in the case of \(\beta =-1\). Similarly, the soliton does not change its position horizontally, but there is a change in the vertical amplitude of the soliton. This change is observed as a decrease in soliton’s amplitude in the cases of both \(\alpha <0\) and \(\alpha >0\) and increasing. Figure 2i illustrates the effect of the parameter \(\beta \); thus, it can be understood that the soliton’s amplitude decreases when \(\beta =-1\) while the soliton’s amplitude increases when \(\beta =1\).

Fig. 2
figure 2

The effect of the parameters on \(\Theta _3(x,1,1)\) for \(w=-0.1, \, p=0.25, \, \sigma =0.65\) with Dset in Eq. (20). a–c for a, d–f for b and g–i for \(\alpha \)

Full size image

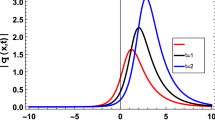
Figure 3 represents the graph of solution functions \(\Theta _5(x,y,t)\) and \(\Phi _5(x,y,t)\) in Eq. (25) considering Dset in Eq. (20) at the parameter values \(w=-0.1, \, a=0.75, \, b=-0.82, \, p=0.25, \, \sigma =0.65, \, \alpha =0.5, \, \beta =0.75.\) 3D graph of \(|\Theta _5(x,y,t)|\) is depicted for \(t=1\) in Fig. 3a, 3D plot of Im\((\Theta _5(x,y,1))\) is demonstrated for \(t=1\) in Fig. 3b and 2D graphs of \(|\Theta _5(x,1,t_f)|\) and Im\((\Theta _5(x,1,1))\) are illustrated in Fig. 3c. Besides, \(t_f=1,2,3\) is the selected fixed time. Figure 3a and c represent the singular soliton of \(|\Theta _5(x,y,1)|\) which has the traveling wave feature. The singularity is \(\lim _{ \begin{array}{c} x\rightarrow \pm x_0, \\ t=t_f \end{array}} |\Theta _5(x,y,t)| \rightarrow \infty \) for Fig. 3a and \(\lim _{ \begin{array}{c} x\rightarrow \pm x_0, \\ t=1 \end{array}} \text {Im}(\Theta _5(x,y,t)) \rightarrow {\mp } \infty \) for Fig. 3b. In Fig. 3d and e, 3D and 2D graphs of \(\Phi _5(x,y,t)\) are plotted at \(t=1\), respectively, and these graphs represent the singular soliton. The Fig. 3d and e show that \(\lim _{ \begin{array}{c} x\rightarrow \pm x_0, \\ t=1 \end{array}} \Phi _5(x,y,t) \rightarrow -\infty \).

Fig. 3
figure 3

The some graphical illustrations of \(\Theta _{5}(x,y,t)\) and \(\Phi _{5}(x,y,t)\) given by Eq. (25) for \(w=-0.1, \, a=0.75, \, b=-0.82, \, p=0.25, \, \sigma =0.65, \, \alpha =0.5, \, \beta =0.75\) with Dset in Eq. (20)

Full size image

The examination of the bright soliton in Fig. 2 is performed on the singular soliton this time in Fig. 4 in the same way. The objective is to investigate whether the parameter effect arises in different ways in different soliton types. Hence, the effect of \(a, \, b\), \(\alpha \) and \(\beta \) parameters on the graph of \(|\Theta _5(x,y,1)|\) represented in Fig. 3a is analyzed for \(\beta ={\mp } 1\). In Fig. 4a, the effect of parameter a is investigated when \(\beta =1\). Besides, it can be seen that the soliton keeps its shape and changes in its position to the right when a is less than zero and increasing. There is a similar behavior if a is greater than zero and increasing. In Fig. 4b, if \(\beta =-1\), a similar behavior is observed as Fig. 4a and there is a reduction effect on the vertical amplitude of the soliton. It is possible to see this effect more precisely in Fig. 4c. Especially, we can observe from the skirts of the soliton in Fig. 4c that the soliton’s amplitude for \(\beta =-1\) (color solid lines) is smaller than the soliton’s amplitude for \(\beta =1\) (color dashed lines). A similar examination is studied for the parameter b in Fig. 4d. The soliton’s amplitude increases when b is less than zero and increasing (color solid lines), and the amplitude of the soliton decreases when b is greater than zero and increasing (color dashed lines) for \(\beta =1\). In Fig. 4e, the soliton’s amplitude increases if b is less than zero and increasing (color solid lines), while the amplitude of the soliton decreases if b is greater than zero and increasing (color dashed lines) for \(\beta =-1\). Figure 4f is depicted to investigate the effect of the parameter \(\beta \) since Fig. 4d and e have similar characters. It is seen from Fig. 4f that the soliton’s amplitude obtained for \(\beta =-1\) is larger than the obtained for \(\beta =1\). The investigation is accomplished for \(\beta =1\) for the \(\alpha \) parameter in Fig. 4g. The soliton’s amplitude increases if both \(\alpha \) is less than zero and increasing and \(\alpha \) is greater than zero and increasing. On the other hand, for \(\beta =-1\), the amplitude of the soliton decreases when both \(\alpha \) is less than zero and increasing and \(\alpha \) is greater than zero and increasing in Fig. 4h. Moreover, it is analyzed from Fig. 4i that the amplitude of the soliton in the case of \(\beta =1\) is larger than in the case of \(\beta =-1\).

Fig. 4
figure 4

The effect of the parameters on \(|\Theta _5(x,1,1)|\) for \(w=-0.1, \, p=0.25, \, \sigma =0.65\) with Dset in eq. (20). a–c for a, d–f for b and g–i for \(\alpha \)

Full size image

Figure 5 shows the plot of solution functions \(\Theta _8(x,y,t)\) and \(\Phi _8(x,y,t)\) in Eq. (28) with Dset in Eq. (20) at the parameter values \(w=0.1, \, a=0.1, \, b=-0.82, \, p=0.25, \, \sigma =0.2, \, \alpha =0.5, \, \beta =0.075.\) 3D graphs of \(|\Theta _8(x,y,t)\) and Im\((\Theta _8(x,y,t)|\) are plotted for \(t=1\) in Fig. 5a and b, respectively. 2D graphs of \(|\Theta _8(x,1,t_f)|\) and Im\(\Theta _8(x,1,1)\) are demonstrated in Fig. 5c. \(t_f=1,2,3\) is the parameter of the selected fixed time. Figure 5a–c illustrate a periodic singular soliton for both \(|\Theta _8(x,y,1)|\) and Im\(\Theta _8(x,y,1)\). The singularity is \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=t_f \end{subarray}} |\Theta _8(x,y,t)| \rightarrow +\infty \), \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=1 \end{subarray}} \text {Im}(\Theta _8(x,y,t)) \rightarrow {\mp } \infty \). 3D and 2D plots for \(\Phi _8(x,y,t)\) are represented for \(t=1\) in Fig. 5d and e, respectively, and these graphs represent the periodic singular soliton. It can be observed from Fig. 5d and e that \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_k, \\ t=1 \end{subarray}} \Phi _8(x,y,t) \rightarrow -\infty \).

Fig. 5
figure 5

The some graphical representations of \(\Theta _{8}(x,y,t)\) and \(\Phi _{8}(x,y,t)\) given by Eq. (28) for \(w=0.1, \, a=0.1, \, b=-0.82, \, p=0.25, \, \sigma =0.2, \, \alpha =0.5, \, \beta =0.075\) with Dset in Eq.  (20)

Full size image

The following graphs represent some selected graphics of Eqs. (46)–(60) obtained for \((2+1)\)-CCME. Figure 6 illustrates \(\Psi _1(x,y,t)\) and \(\Gamma _1(x,y,t)\) given in Eq. (46) at the parameter values \(w=-0.4, \, a=0.25, \, b=2.5\) considering the combination of Mset1 given in Eq. (45). 3D plots of \(|\Psi _1(x,y,t)|\) and Im\((\Psi _1(x,y,t))\) are depicted for \(t=1\) in Fig. 6a and b, respectively. Moreover, 2D plots of \(|\Psi _1(x,1,t_f)|\) and Im\((\Psi _1(x,1,1))\) are plotted together in Fig. 6c. Both functions have a singular soliton. The singularity is \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=t_f \end{subarray}} |\Psi _1(x,1,t)| \rightarrow +\infty \) and \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=1 \end{subarray}} \text {Im}(\Psi _1(x,1,t)) \rightarrow {\mp } \infty \). 3D and 2D graphs of \(\Gamma _1(x,y,t)\) are illustrated for \(t=1\) in Fig. 6d and e, respectively; besides, these graphs show the singular soliton. It can be observed from Fig. 6d and e that \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=1 \end{subarray}} \Gamma _1(x,1,t) \rightarrow -\infty \). Figure 7 shows the graph of \(\Psi _7(x,y,t)\) and \(\Gamma _7(x,y,t)\) in Eq. (52) for parameter values \(w=-0.04, \, r=-2, \, b=2.5\) with a combination of Mset2 in Eq. (45). Figure 7a and b represent the 3D graphs of \(|\Psi _7(x,y,t)|\) and Im\((\Psi _7(x,y,t))\) for \(t=1\), respectively. Moreover, Fig. 7c illustrates the 2D plots of these functions together. It can be observed from Fig. 7a and c that \(|\Psi _7(x,1,1)|\) is a dark soliton while Im\((\Psi _7(x,1,1))\) is a periodic soliton with different amplitudes. Furthermore, 3D and 2D plots of \(\Gamma _7(x,y,t)\) are displayed for \(t=1\) in Fig. 7d and e which represent the bright soliton with traveling wave behavior, respectively. Finally, Fig. 8 indicates the graph of \(\Psi _8(x,y,t)\) and \(\Gamma _8(x,y,t)\) in Eq. (53) with parameters \(w=-0.4,\, a=-2, \, b=2.5\) and Mset2 given in Eq. (45). Figure 8a–c show the periodic singular soliton for \(|\Psi _8(x,y,t_f)|\) and Im\((\Phi _8(x,y,1))\). Here, \(t_f=1,2,3\) presents the selected fixed time. From Fig. 8a and c, it can be observed that \(\lim _{ \begin{subarray}{c} x\rightarrow \pm x_0, \\ t=t_f \end{subarray}} |\Psi _8(x,1,t)| \rightarrow +\infty \) for \(|\Psi _8(x,y,t)|\). 3D and 2D graphs are plotted for \(\Gamma _8(x,y,t)\) at \(t=1\) in Fig. 8d and e, which offer the periodic singular soliton, respectively. Besides, \( \lim _{ \begin{subarray}{c} x\rightarrow \pm x_f, \\ t=t_f \end{subarray} } |\Psi _8(x,1,t)| \rightarrow -\infty .\)

Fig. 6
figure 6

The some graphical projections of \(\Psi _{1}(x,y,t)\) and \(\Gamma _{1}(x,y,t)\) in Eq. (46) for \(w=-0.4, \, a=0.25, \, b=2.5\) with Mset1 in Eq. (45)

Full size image
Fig. 7
figure 7

The some graphical projections of \(\Psi _{7}(x,y,t)\) and \(\Gamma _{7}(x,y,t)\) given by Eq. (52) for \(w=-0.04, \, r=-2, \, b=2.5\) with Mset2 in Eq. (45)

Full size image
Fig. 8
figure 8

The some graphical projections of \(\Psi _{8}(x,y,t)\) and \(\Gamma _{8}(x,y,t)\) given by Eq. (53) for \(w=0.4, \, a=-2, \, b=2.5\) with Mset2 in Eq. (45)

Full size image

A brief review of the achieved results

  1. a.

    By applying the method successfully, a variety of soliton solutions were obtained for both problems, and their graphical representations were given.

  2. b.

    One of the most fundamental aims of this study is the investigation of the parameter effects on the soliton behavior, including the coupling parameters for the (2+1)-DSE equation. The following results were obtained for the bright soliton and singular soliton, respectively.

For the bright soliton in Fig. 1a:

  • If \(\beta =1\), \(a<0\), and a are increasing, then the soliton moves to the right on the horizontal axis, and the vertical amplitude of the soliton (height) decreases. If \(\beta =1\), \(a>0\) and increasing, the soliton moves to the right on the horizontal axis, and the soliton’s amplitude (height) increases (Fig. 2a). Thus, "the opposite sign of the parameter a" has an inverse effect on the soliton’s amplitude. If \(\beta =-1\), \(a<0\) (or \(a>0\)) and increasing, then the same effects are obtained as in Fig. 2a. But the amount of change in vertical amplitude remains smaller than in Fig. 2a (Fig. 2b). If \(\beta \) takes the same absolute but opposite sign values (\(\beta =-1\) or \(\beta =1\)), the soliton’s amplitude at positive \(\beta \) values is larger than the amplitude of the soliton at negative \(\beta \) values (Fig. 2c).

  • If \(\beta =1\), \(b<0\) and increasing, then there is no change in the position of the soliton horizontally, but the position of the soliton’s apex changes. This change arises from an increase in the soliton’s amplitude. If \(\beta =1\), \(b>0\) and increasing, then the soliton’s amplitude decreases (Fig. 2d). If \(\beta =-1\), \(b<0\) and increasing, then the same effect is observed as in Fig. 2d. That is, the soliton’s amplitude increases. If \(\beta =-1\), \(b>0\), and increasing, then the soliton’s amplitude decreases (Fig. 2e). When \(\beta =-1\), its effect on the soliton’s amplitude is an increment compared to the case when \(\beta =1\) (Fig. 2f).

  • If \(\beta =1\), \(\alpha <0\) (or \(\alpha >0\)) and increasing, then the soliton does not change its position on the horizontal axis but the peak of the soliton increases (Fig. 2g). If \(\beta =-1\), \(\alpha <0\) (or \(\alpha >0\)) and increasing, then the soliton does not change its position on the horizontal axis but the peak of the soliton decreases (Fig. 2h). If \(\beta =-1\) or \(\beta =1\), then the soliton’s amplitude decreases (Fig. 2i).

For the singular soliton in Fig. 3a:

  • When \(\beta =1\), \(a<0\) (or \(a>0\)) and increasing, then the soliton moves to the right on the horizontal axes (Fig. 4a). If \(\beta =-1\), \(a<0\) (or \(a>0\)) and increasing, then we observed a similar behavior (Fig. 4b). Although, Fig. 4a and b reflect the same behavior, the soliton’s amplitude for \(\beta =-1\) is smaller than the soliton’s amplitude for \(\beta =1\) (Fig. 4c).

  • When \(\beta =1\), \(b<0\) and increasing, then the soliton’s amplitude increases. When \(\beta =1\), \(b>0\) and increasing, then the soliton’s amplitude decreases (Fig. 4d). When \(\beta =-1\), \(b<0\), and increasing, then the soliton’s amplitude increases. When \(\beta =-1\), \(b>0\) and increasing, then the soliton’s amplitude decreases (Fig. 4e). When \(\beta =-1\) or \(\beta =1\), the soliton’s amplitude for \(\beta =-1\) is larger than the for \(\beta =1\) (Fig. 4f).

  • When \(\beta =1\), \(\alpha <0\) (or \(\alpha >0\)) and increasing, the soliton’s amplitude increases (Fig. 4g). When \(\beta =-1\), \(\alpha <0\) (or \(\alpha >0\)) and increasing, the soliton’s amplitude decreases (Fig. 4h). Besides, the soliton’s amplitude in the case of \(\beta =1\) is larger than in the case of \(\beta =-1\) (Fig. 4i).

Both from the graphs and explanations of the graphs presented in this section and from the issues summarized above, it is obvious that the parameters in the presented NLPDEs are important in terms of soliton dynamics. Some models already contain some limitations, as presented in the literature. These constraints can be that sometimes a parameter can only take the value \({\mp } 1\), sometimes it can only be positive, and sometimes it can only be a positive integer. In other cases, these parameters are generally presented as non-zero constants or real constants. However, although such constants appear as coefficients in the relevant model equations, they are of great importance in terms of soliton dynamics due to the function of the terms that they represent. For example, in nonlinear optics, the soliton is a result of the interaction between group velocity dispersion and self-phase modulation. From this perspective, this interaction is based on a sensitive balance, and the coefficients represented by both terms are important in this context. In order to see the result of this interaction, the relevant coefficients need to be selected to observe this sensitive balance. The analysis in this study is carried out considering this basic framework. First of all, a specific soliton form is obtained for specific parameter values, and then the change in the soliton form is observed for different values of the relevant parameters. In light of the work done, the parameters have a significant effect on the soliton behavior, and this effect occurs in different ways depending on the soliton shapes. Each problem has its own unique character and physical meaning, and more study and interpretation in this field will also contribute to the understanding of many physical phenomena. The understanding achieved from examining soliton solutions of (\(2+1\))-DSE and (\(2+1\))-CCMS can be utilized to predict and comprehend wave phenomena in fluid dynamics, including but not limited to water waves and ocean currents. Moreover, solitons have a significant influence in plasma physics. Thus, the produced soliton solutions can provide an understanding of plasma dynamics and turbulence. Analyzing soliton dynamics within the framework of (\(2+1\))-DSE and (\(2+1\))-CCMS can lead to enhanced designs for optical communication networks.

5 Conclusion and future recommendations

In this paper, we looked at the \((2+1)\)-DSE as well as the complicated \((2+1)\)-CCMS and its plethora of analytical soliton solutions. Analytical traveling wave solutions in such equations are extremely valuable, not only in numerical theories but also in analytical theories. To have the analytical soliton solutions of the investigated models, we used an outstanding analytical technique. The study is not limited to obtaining analytical soliton solutions. Especially, the effects of DSE parameters on soliton dynamics were examined, the results were presented graphically, and detailed physical comments were made. As far as we know, there is no previous study in the literature for the \((2+1)\)-DSE equation, which is related to the effect of the parameters involving coupling parameters on the soliton dynamics. Therefore, this study significantly contributes to the literature by not only examining the effects of parameters and coupling coefficients of the \((2+1)\)-DSE on soliton behavior but also by providing novel insights into the dynamics of solitons under various parameter regimes. We demonstrated that the characteristics of soliton solutions could reflect the spread of propagation on wavefronts and that they had an acceptable reliance on parameter values. All of the solutions produced satisfied the original equations. The results demonstrated that the approach was both resilient and efficient in locating precise solutions to a wide range of nonlinear models. Studying soliton solutions and examining the influence of the parameters on the behavior of the soliton offers insights into main nonlinear wave dynamics, has useful applications in diverse fields, and contributes to the development of mathematical and physical sciences. In order to shed light on future studies, it may be aimed at retrieving new analytical solutions for \((2+1)\)-DSE and \((2+1)\)-CCMS using diverse analytical approaches. Researchers can investigate how to obtain different types of solitons for \((2+1)\)-DSE and \((2+1)\)-CCMS. In future studies, it may be focused on examining the soliton behavior of the newly produced solitons according to the parameter effects. Additionally, fractional and stochastic forms of \((2+1)\)-DSE and \((2+1)\)-CCMS can be analyzed, and their analytical solutions can be obtained with the help of the different analytical methods. Multi-soliton solution, soliton interaction, bifurcation, phase portrait, and sensitivity analysis are among the other titles that can be added.