1 Introduction

The studies of the nonlinear partial differential equations have improved consistently with significant progress over many decades. These equations have appeared in numerus scientific field, such as plasma physics, fluid dynamics, electromagnetism, quantum mechanics, signal processing, chemical physics, biology, optics, turbulence, aerodynamics, hydrodynamics, and so on. The special classes of the nonlinear partial differential equations are the nonlinear evolution equations. The general nonlinear evolution equation was introduced as (Chen et al. 2003)

$$\frac{\partial^2 u}{{\partial t^2 }} + a\frac{\partial^2 u}{{\partial x^2 }} + bu + cu^q + du^{2q - 1} = 0.$$

Here \(a,b,c,d\) and \(q \ne 1\) are arbitrary constants. When \(q = 3\) and \(d = 0\), the special form of this equation is expressed as (Bai 2001)

$$\frac{\partial^2 u}{{\partial t^2 }} + a\frac{\partial^2 u}{{\partial x^2 }} + bu + cu^3 = 0.$$
(1)

Equation (1) also contains some important nonlinear equations that are frequently used in mathematical physics. An important one of them is the Landau–Ginzburg–Higgs equation. When \(a = - 1\), \(b = - g^2\) and \(c = h^2\), Eq. (1) becomes the Landau–Ginzburg–Higgs equation in the form

$$\frac{\partial^2 u}{{\partial t^2 }} - \frac{\partial^2 u}{{\partial x^2 }} - g^2 u + h^2 u^3 = 0$$
(2)

where \(u\left( {x,t} \right)\) defines the electrostatic potential of ion-cyclotron wave, \(t\) and \(x\) state the temporal and spatial coordinates, \(g\) and \(h\) are real parameters. This equation was suggested by Landau and Ginzburg to describe drift cyclotron waves and superconductivity for steady ion-cyclotron waves in nonhomogeneous plasma (Cyrot 1973). Besides, Eq. (1) becomes the Duffing equation, the Klein Gordon equation, the Phi-4 equation, and the Sine–Gordon equation depend on \(a\) \(b\) and \(c\) arbitrary constants.

Recently, many methods have been used to obtain the solutions of the Landau–Ginzburg–Higgs equation. These are the Runge–Kutta method (Hu et al. 2009), the ansatz method (Çevikel et al. 2013; Guner et al. 2017), \((G^{\prime}/G, 1/G)\)-expansion method (Iftikhar et al. 2013; Zulqarnain et al. 2023), the first integral method (Bekir and Ünsal 2013), a new modified simple equation method (Irshad et al. 2017), the modified exponential function method (Kırcı et al. 2022), the Bernoulli sub-equation function method (Islam and Akbar 2020), the generalized Kudryashov method (Barman et al. 2021a, b), the extended tanh method (Barman et al. 2021a, b), the sine–Gordon expansion method (Kundu et al. 2021), the local fractional variational iteration method (Deng and Ge 2021), the power index method (Ahmad et al. 2023a, b), the generalized projective Riccati method (Asjad et al. 2023), the inverse scattering transformation method (Ali et al. 2023), the modified \(\left( {G^{\prime}/G^2 } \right)\)-expansion method (Zulqarnain et al. 2023), a new auxiliary equation method (Zulqarnain et al. 2023), the Khater method (Faridi and AlQahtani 2024), the \(G^{\prime}/\left( {bG^{\prime} + G + a} \right)\)-expansion method (Raza et al. 2024), a new extended direct algebraic method (Alqurashi et al. 2023), the polynomial method (Rizvi et al. 2024), the Sardar-sub equation method (Ahmad et al. 2023a, b), the energy balance method (Ahmad et al. 2023a, b), the generalized exponential rational function method (Al-Amin and Islam 2023), the simple equation method (Chankaew et al. 2023), and the tanh method (Rakah et al. 2023). Among these methods, the power index method includes the solutions in terms of the Jacobi elliptic function. This method used only one type of Jacobi elliptic function in its solutions. However, there are 12 Jacobi elliptic functions in the literature.

The basic Jacobi elliptic functions are given as follows:

$${\text{sn}}\xi = {\text{sn}}\left( {\xi {|}m^2 } \right), \quad {\text{cn}}\xi = {\text{cn}}\left( {\xi {|}m^2 } \right), \quad {\text{dn}}\xi = {\text{dn}}\left( {\xi {|}m^2 } \right).$$

Here, \(m\) a complex number and it symbolizes the modules of the elliptic function. When the \(m\) is real number, it takes a value between 0 and 1. Taking quotients and reciprocals of these functions, Glaisher discovered the 9 different elliptic functions denoted by ds, cs, ns, dc, nc, sc, nd, cd, and sd. Besides, when \(m = 1\) and \(m = 0\), Jacobi elliptic functions convert into hyperbolic and trigonometric functions, respectively. More details of the Jacobi elliptic functions and properties of the Jacobi elliptic functions can be seen in (Erdelyi et al. 1953; Abramowitz and Stegun 1972).

The analytical method based upon 12 Jacobi elliptic functions has been utilized to attain the solutions for several differential equations in the literature (Yan 2003; Liu et al. 2004, 2001; Wang et al. 2005; Zhang 2007; El-Sabagh and Ali 2008; Yomba 2010; El-Sheikh et al. 2020). This method has many advantages compared to other methods in the literature. The solutions can be obtained in general form that includes hyperbolic, trigonometric and rational functions by utilizing the proposed method. The complex valued solutions and the soliton solutions are also found. Besides, the suggested method does not need initial and boundary conditions, perturbation, linearization. Moreover, this method covers the solutions of numerous methods such as sech, sine–cosine ansatz, and tanh methods. Furthermore, the presented method is applicable to various kind of partial differential equations that transform into ordinary differential equations.

The goal of the proposed method is to attain the solution \(u\left( \xi \right)\) of the nonlinear ordinary differential equation in the form

$$u\left( \xi \right) = \mathop \sum \limits_{j = 0}^N a_j G^j \left( \xi \right)$$

where \(N\) is the constant to be calculated and \(a_j\) is unknown coefficient. \(G(\xi )\) is the solution of the auxiliary ordinary differential equation expressed as.

$$\left( {dG/d\xi } \right)^2 = PG^4 \left( \xi \right) + QG^2 \left( \xi \right) + R$$
(3)

Here \(P\), \(Q\), and \(R\) are constants. A special form of the Duffing equation is gained by differentiating Eq. (3) as

$$G^{^{\prime\prime}} \left( \xi \right) = 2PG^3 \left( \xi \right) + QG\left( \xi \right).$$

This equation emerges a mathematical model in numerous physical systems (Kovacic and Brennan 2011). Since there are not many solutions of Eq. (3) in the literature, theorems and corollaries are proposed to get new solutions of this equation (Dascıoglu and Ünal 2021). The aim of this study is to gain the widest set of solutions of the Landau–Ginzburg–Higgs Eq. (2) by utilizing this new solutions of the auxiliary ordinary differential Eq. (3).

2 Some theorems and Corollaries

In this section, theorems and corollaries are introduced for the new solutions of Eq. (3) (Dascıoglu and Ünal 2021). Some of them are given below.

Theorem 2.1.

Let \(G(\xi )\) be a solution of Eq. (3). When \(P\), \(Q\), and \(R\) in Eq. (3) are replaced by \(\omega^2 P\), \(\omega^2 Q\), and \(\omega^2 R\), the new solution turns into \(G(\omega \xi )\). Here, \(\omega\) be any complex or real constant that can also depends on \(m\).

Theorem 2.2.

Let \(G(\xi ) \ne 0\) be a solution of Eq. (3). When \(P\) and \(R\) are interchanged in Eq. (3), the solution turns into \(1/G(\xi )\).

Theorem 2.3.

Let \(G(\xi ) \ne 0\) be a solution of Eq. (3) and \(X\), \(Y\) are an arbitrary constants. When \(P\), \(Q\), and \(R\) in Eq. (3) are replaced by \(P/X^2\), \(Q - 6PY/X\), and \(8PY^2 - 4QXY\) such that \(PY^2 = RX^2\), the solution turns into \(XG\left( \xi \right) + Y/G\left( \xi \right)\).

Corollary 2.1.

When \(X = K\) and \(Y = 0\), that is \(P\) and \(R\) in Eq. (3) are replaced by \(P/K^2\) and \(K^2 R\), the solution turns into \(KG(\xi )\). Here, \(K\) be any complex or real constant that can also depends on \(m\).

Corollary 2.2.

When \(X = i\) and \(Y = 0\), \(P\) and \(R\) are replaced by \(-P\) and \(-R\), respectively. Hence, the solution turns into i \(G(\xi )\).

Corollary 2.3.

When \(X = \sqrt {T}\) and \(Y = 0\), \(P\) and \(R\) are replaced by \(P/T\) and \(RT\), respectively. Hence, the solution turns into \(\sqrt {T} G(\xi )\).

Corollary 2.4.

When \(X = 1/\sqrt {T}\) and \(Y = 0\), \(P\) and \(R\) are replaced by \(PT\) and \(R/T\), respectively. Hence, the solution turns into (1/\(\sqrt {T}\))\(G(\xi )\).

Using these theorems and corollaries, infinitely various solutions can be obtained depend on \(\omega\), \(K\), and \(m\). The elliptic and elementary function solutions of Eq. (3) given by tables in (Dascıoglu and Ünal 2021). It is observed that these tables provide the largest set of solutions of the auxiliary ordinary differential Eq. (3) in the literature (Elgarayhi 2005; Hua-Mei 2005; Chen and Wang 2006; Zayed 2009; Lin et al. 2009; Shang 2010; Ali 2011; Ebaid and Aly 2012; Alofi and Abdelkawy 2012; Li et al. 2012; Zhao 2013; Zheng and Feng 2014; Liu 2021). When the studies in the literature are analyzed in detail, it is seen that some solutions are the same or cover each other. For example, \({\text{cn}}\left( {\omega \xi } \right)/\left( {1 \pm {\text{sn}}\left( {\omega \xi } \right)} \right)\) and \({\text{nc}}\left( {\omega \xi } \right) \pm {\text{sc}}\left( {\omega \xi } \right)\) are the same. Multiplying the denominator and numerator by conjugate and utilizing the relations between Jacobi elliptic functions, it can be seen that these two solutions are equal to each other. Therefore, the elliptic function solutions given by table are presented as linearly independent as possible (Dascıoglu and Ünal 2021).

3 Solutions of the Landau–Ginzburg–Higgs equation

In this part of the study, the Landau–Ginzburg–Higgs Eq. (2) is examined. Utilizing the wave transformation

$$\xi = x - ct$$

such that \(c\) is wave velocity, Eq. (2) turns into an ordinary differential equation in the form

$$(c^2 - 1)\frac{d^2 u}{{d\xi^2 }} - g^2 u + h^2 u^3 = 0$$
(4)

where \(c^2 - 1 \ne 0\).

\(N = 1\) is obtained by balancing the highest order nonlinear term with the highest order linear term in Eq. (4). Therefore, the solution of Eq. (4) is stated as

$$u\left( \xi \right) = a_0 + a_1 G\left( \xi \right).$$

Utilizing Eq. (3), and differentiating the above equation two times, the second derivative is expressed as

$$u^{\prime \prime} = a_1 QG + 2a_1 PG^3 .$$

Substituting this derivative into Eq. (4), third order polynomial in G is found. The coefficients are taken as zero and the following system of equations is gained,

$$\begin{aligned} - g^2 a_0 + h^2 a_0^3 & = 0 \\ c^2 Qa_1 - Qa_1 - g^2 a_1 + 3h^2 a_0^2 a_1 & = 0 \\ 3h^2 a_0 a_1^2 & = 0 \\ 2c^2 Pa_1 - 2Pa_1 + h^2 a_1^3 & = 0. \\ \end{aligned}$$

Solving the above system, the unknown coefficients are obtained \(a_0 = 0\), \(a_1 = \pm \frac{g}{h}\sqrt { - 2P/Q}\) and \(a_0 = \pm g/h\), \(a_1 = 0\) such that \(Q = g^2 /\left( {c^2 - 1} \right)\). When \(A = g/h\) is taken, the solutions of Eq. (4) are

$$u = \pm A\sqrt {{\frac{ - 2P}{Q}}} G, u = \pm A.$$

Substituting the \(G\), \(P\), and \(Q\) given in Ref. (Dascıoglu and Ünal 2021) into above solutions, the solutions of Eq. (4) are gained. Some of them are constant solutions such as \(u = \pm A\) and \(u = 0\) are not shown in Tables 1, 2 and 3. The elementary solutions of Eq. (4) are demonstrated in Table 1. Clearly observed that the solutions are obtained as complex, rational, hyperbolic, and trigonometric functions. The Jacobi elliptic function solutions of Eq. (4) are illustrated in Table 2. It is seen that, the soliton solutions and the complex valued solutions are found in this table. In Table 2, infinitely various solutions can be also obtained depend on \(\omega\) and \(m\). Therefore, more solutions are gained than the methods in the literature. In Table 3, utilizing the Jacobi elliptic functions for \(m = 1\) and \(m = 0\) and the solutions in Table 2, the elementary function solutions of Eq. (4) are demonstrated. For specially selected values of \(K\) and \(Q\), some of these solutions are the same as the solutions in Table 1.

Table 1 The elementary solutions for Eq. (4)
Full size table
Table 2 The Jacobi elliptic function solutions for Eq. (4)
Full size table
Table 3 The solutions of Table 2 when \(m = 0\) and \(m = 1\)
Full size table

Remark 3.1.

Solutions of Eq. (3) that have the same product \(PR\) can be expressed as a group according to their \(Q\) values. Therefore, there are sixteen different groups in Table 2 as shown in Dascıoglu and Ünal (2021).

4 Applications

In this part of the work, the solutions of four examples are given. These examples are also demonstrated by two- and three-dimensional graphics. Besides, the solutions are illustrated by the Mathematica in all figures.

Example 1 Let us examine the Landau–Ginzburg–Higgs Eq. (2) for \(g = h = 1\); that is

$$\frac{\partial^2 u}{{\partial t^2 }} - \frac{\partial^2 u}{{\partial x^2 }} - u + u^3 = 0.$$

The solutions of this equation are

$$u = \pm \sqrt {{\frac{ - 2P}{Q}}} G, u = \pm 1.$$

When \(\omega = m = 1\), the \(Q = - 2\) is found for the first case in Table 2. The condition \(Q = g^2 /\left( {c^2 - 1} \right)\) is also satisfied for \(c = \sqrt {2} /2\). Thus, the transformation becomes \(\xi = x - \sqrt {2} t/2\). The solutions of the first case in Table 2 are

$$u = \pm m\sqrt {{\frac{2}{m^2 + 1}}} {\text{sn}}\left( {\omega \xi } \right).$$

When \(\omega = m = 1\), these solutions turn into

$$u = \pm {\text{tanh}}\left( {x - \frac{{\sqrt {2} }}{2}t} \right).$$

In Figs. 1 and 2, these solutions are demonstrated for \(- 30 \le x \le 30\) and \(0 \le t \le 10\). They are also called an antikink soliton and a kink soliton, respectively (Remoissenet 1993). Therefore, the antikink type travelling wave solution is represented in Fig. 1 and kink type travelling wave solution is represented in Fig. 2. Moreover, the same solutions are illustrated with 2D plot for \(- 30 \le x \le 30\) at \(t = 3\) in Figs. 3 and 4.

Fig. 1
figure 1

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = - {\text{tanh}}\left( {x - \sqrt {2} t/2} \right).\)

Full size image
Fig. 2
figure 2

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = {\text{tanh}}\left( {x - \sqrt {2} t/2} \right).\)

Full size image
Fig. 3
figure 3

Two-dimensional graphic of the solution \(u\left( {x,3} \right) = - {\text{tanh}}\left( {x - 3\sqrt {2} /2} \right).\)

Full size image
Fig. 4
figure 4

Two-dimensional graphic of the solution \(u\left( {x,3} \right) = {\text{tanh}}\left( {x - 3\sqrt {2} /2} \right).\)

Full size image

Example 2 Let us examine the Landau–Ginzburg–Higgs Eq. (2) for \(g = 2\) and \(h = 1\); that is

$$\frac{\partial^2 u}{{\partial t^2 }} - \frac{\partial^2 u}{{\partial x^2 }} - 4u + u^3 = 0.$$

The solutions of this equation are

$$u = \pm 2\sqrt {{\frac{ - 2P}{Q}}} G, u = \pm 2.$$

When \(\omega = m = 1\), the \(Q = 1\) is found for the second case in Table 2. The condition \(Q = g^2 /\left( {c^2 - 1} \right)\) is satisfied for \(c = \sqrt {5}\). Thus, the transformation becomes \(\xi = x - \sqrt {5} t\). The solutions of the second case in Table 2 are

$$u = \pm 2im\sqrt {{\frac{ - 2}{{2m^2 - 1}}}} {\text{cn}}\left( {\omega \xi } \right).$$

When \(\omega = m = 1\), these solutions turn into

$$u = \pm 2\sqrt {2} {\text{sech}}\left( {x - \sqrt {5} t} \right).$$

In Figs. 5 and 6, these solutions are demonstrated for \(- 10 \le x \le 10\) and \(1 \le t \le 3\). These figures represent the travelling solitary wave solution of the Landau–Ginzburg–Higgs Eq. (2). Moreover, the same solutions are illustrated with 2D plot for \(- 10 \le x \le 10\) at \(t = 2\) in Figs. 7 and 8.

Fig. 5
figure 5

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = 2\sqrt {2} {\text{sech}}\left( {x - \sqrt {5} t} \right).\)

Full size image
Fig. 6
figure 6

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = - 2\sqrt {2} {\text{sech}}\left( {x - \sqrt {5} t} \right).\)

Full size image
Fig. 7
figure 7

Two-dimensional graphic of the solution \(u\left( {x,2} \right) = 2\sqrt {2} {\text{sech}}\left( {x - 2\sqrt {5} } \right).\)

Full size image
Fig. 8
figure 8

Two-dimensional graphic of the solution \(u\left( {x,2} \right) = - 2\sqrt {2} {\text{sech}}\left( {x - 2\sqrt {5} } \right).\)

Full size image

Example 3 Let us examine the Landau–Ginzburg–Higgs Eq. (2) for \(g = 1\) and \(h = 2\); that is

$$\frac{\partial^2 u}{{\partial t^2 }} - \frac{\partial^2 u}{{\partial x^2 }} - u + 4u^3 = 0.$$

The solutions of this equation are

$$u = \pm \frac{1}{2}\sqrt {{\frac{ - 2P}{Q}}} G, u = \pm \frac{1}{2}.$$

When \(m = 0\) and \(\omega = i\), the \(Q = 1\) is found for the second case in Table 2. The condition \(Q = g^2 /\left( {c^2 - 1} \right)\) is satisfied for \(c = \sqrt {2}\). Thus, the transformation becomes \(\xi = x - \sqrt {2} t\). The solutions of the second case in Table 2 are

$$u = \pm \frac{1}{2}\sqrt {{\frac{ - 2(1 - m^2 )}{{2m^2 - 1}}}} {\text{nc}}\left( {\omega \xi } \right).$$

When \(m = 0\) and \(\omega = i\), these solutions turn into

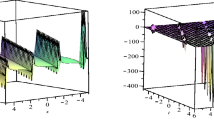
$$u = \pm \frac{{\sqrt {2} }}{2}{\text{sec}}\left( {i(x - \sqrt {5} t)} \right).$$

In Figs. 9 and 10, these solutions are demonstrated for \(- 20 \le x \le 20\) and 0 \(\le t \le 5\). Moreover, the same solutions are illustrated with 2D plot for \(- 20 \le x \le 20\) at \(t = 3\) in Figs. 11 and 12. It is seen from these figures that the wave amplitudes go to infinity.

Fig. 9
figure 9

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = (\sqrt {2} /2){\text{sec}}\left( {i(x - \sqrt {2} t)} \right).\)

Full size image
Fig. 10
figure 10

Three-dimensional graphic of the solution \(u\left( {x,t} \right) = - (\sqrt {2} /2){\text{sec}}\left( {i(x - \sqrt {2} t)} \right).\)

Full size image
Fig. 11
figure 11

Two-dimensional graphic of the solution \(u\left( {x,3} \right) = (\sqrt {2} /2){\text{sec}}\left( {i(x - 3\sqrt {5} )} \right).\)

Full size image
Fig. 12
figure 12

Two-dimensional graphic of the solution \(u\left( {x,3} \right) = - (\sqrt {2} /2){\text{sec}}\left( {i(x - 3\sqrt {5} )} \right).\)

Full size image

Example 4 Let us examine the Landau–Ginzburg–Higgs Eq. (2) for \(g = h = 2\); that is

$$\frac{\partial^2 u}{{\partial t^2 }} - \frac{\partial^2 u}{{\partial x^2 }} - 4u + 4u^3 = 0.$$

The solutions of this equation are

$$u = \pm \sqrt {{\frac{ - 2P}{Q}}} G, u = \pm 1.$$

For \(\omega = \sqrt {2}\), the solutions of the fifth case in Table 2 are

$$u = \pm i\sqrt {{\frac{ - 2}{{2 - m^2 }}}} {\text{dn}}\left( {\sqrt {2} \xi } \right).$$

In Figs. 13 and 14, these solutions are illustrated for 0 \(\le m \le 1\) and \(- 10 \le \xi \le 10\). Besides, the same solutions are demonstrated with 2D plot for \(- 10 \le \xi \le 10\) and \(m = 0.3\) in Figs. 15 and 16. It can be observed from these figures that solitons are occurred. Solitons are nonlinear waves in mathematics and physics that maintain their shape, amplitude, and velocity while moving along the axes. More details for solitons can be accessible in (Guo et al. 2020a, b; Guo et al. 2020a, b; Akram and Sajid 2021; Akram et al. 2021, 2022a, b; 2023; Sadaf et al. 2022; Arnous et al. 2022; Wang et al. 2022).

Fig. 13
figure 13

Three-dimensional graphic of the solution \(u\left( {\xi ,m} \right) = i\sqrt {{\frac{ - 2}{{2 - m^2 }}}} {\text{dn}}\left( {\sqrt {2} \xi } \right).\)

Full size image
Fig. 14
figure 14

Three-dimensional graphic of the solution \(u\left( {\xi ,m} \right) = - i\sqrt {{\frac{ - 2}{{2 - m^2 }}}} {\text{dn}}\left( {\sqrt {2} \xi } \right).\)

Full size image
Fig. 15
figure 15

Two-dimensional graphic of the solution \(u\left( {\xi ,0.3} \right) = i\sqrt {{\frac{ - 2}{{2 - 0.3^2 }}}} {\text{dn}}\left( {\sqrt {2} \xi } \right).\)

Full size image
Fig. 16
figure 16

Two-dimensional graphic of the solution \(\left( {\xi ,0.3} \right) = - i\sqrt {{\frac{ - 2}{{2 - 0.3^2 }}}} {\text{dn}}\left( {\sqrt {2} \xi } \right).\)

Full size image

5 Conclusions

The suggested method depends upon the Jacobi elliptic functions was considered to find the exact solutions of the Landau–Ginzburg–Higgs equation in this study. When solving this equation, the auxiliary ordinary differential Eq. (3) was utilized. Some theorems and corollaries were given for solutions of Eq. (3). Using these solutions, many elliptic and elementary solutions of the Landau–Ginzburg–Higgs equation were attained. The solutions of the Landau–Ginzburg–Higgs equation were obtained in the form containing the hyperbolic, trigonometric, and rational functions. The soliton solutions and the complex valued solutions were also gained by suggested method. These solutions were demonstrated by tables. Some of them were illustrated in figures.

In the literature, the power index method (Ahmad et al. 2023a, b) contains the solutions in term of the Jacobi elliptic function when solving the Landau–Ginzburg–Higgs equation. The solutions found by this method include only one of the Jacobi elliptic functions. The other 11 types of Jacobi elliptic functions were not used by this method. However, the solutions found by the proposed method include 12 types of Jacobi elliptic functions. When compared with the power index method, it is clearly observed that more solutions were obtained with the suggested method. Because 6 solutions for 4 cases were gained by the power index method, while 248 solutions for 16 different cases were found by this method. Besides, infinitely various solutions can be found depend upon \(m\) and \(\omega\) in Table 2 by our method. Moreover, many differential equations such as the Landau–Ginzburg–Higgs equation can be solved by utilizing the solutions of auxiliary equation. Furthermore, these solutions can be effective and useful for various solution methods. Thus, these solutions contain the largest set of solutions in the literature.