Off-axis vortex Gaussian beams in strongly nonlocal nonlinear media with oblique incidence

Abstract

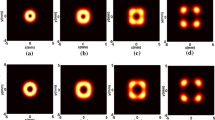
The off-axis vortex Gaussian beam (OavGB) in strongly nonlocal nonlinear media (SNNM) with oblique incidence showed novel transmission characteristics. When the off-axis vortex parameters were not equalled to the intensity distribution parameters, the analytical expression for the propagation of the OavGB in SNNM was obtained by using the ABCD matrix method. The expression for the second-order moment beamwidth and the trajectory equation for the center of the beam’s mass were obtained by analytical method. According to numerical simulations, the projection of the mass’s center on the cross-section was found to be an ellipse, a line segment, or a circle, with the direction of rotation of the projected trajectory around the z-axis depending on the direction of the orbital angular momentum, and the direction of rotation of the beam depending on the sign in front of the imaginary part of the vortex point. The direction of the OavGB’s rotation and the direction of revolution of the mass’s center may be the same or opposite, But the rotation period of the beam and the revolution period of the mass’s center were equated. The projected trajectory of the mass’s center of the beam on the cross-section can be controlled by the magnitude of the parameters a, b, c, d, $\zeta$, f. These laws can be used to control beam transmission paths and information encoding.

Appendix

Calculate the integral of Eqs. (5) and (6) then Then we can obtain the expressions of mass center

$$\begin{aligned} x_c&=A\eta _x-iB\xi _x \end{aligned}$$

(35)

$$\begin{aligned} y_c&=A\eta _y-iB\xi _y \end{aligned}$$

(36)

where A and B are the elements of ABCD matrix:

$$\begin{aligned} \left( \begin{array}{cc} A&{}B\\ C&{}D \end{array}\right) = \left( \begin{array}{cc} \textrm{cos}\left( \sqrt{{\gamma ^{2}}{{\textrm{P}}_{0}}} z\right) &{} { - \frac{{1}}{{\sqrt{{\gamma ^{2}}{{\textrm{P}}_{0}}} }}\textrm{sin} \left( \sqrt{{\gamma ^{2}}{{\textrm{P}}_{0}}} z\right) }\\ {\sqrt{{\gamma ^{2}}{{\textrm{P}}_{0}}} \textrm{sin} \left( \sqrt{{{\gamma }^{2}}{{\textrm{P}}_{0}}} z\right) }&{} \textrm{cos}\left( \sqrt{{\gamma ^{2}}{{\textrm{P}}_{0}}} z\right) \end{array}\right) \end{aligned}$$

(37)

and

$$\begin{aligned} \eta _x&=\frac{\displaystyle \int _{-\infty }^{\infty } \int _{-\infty }^{+\infty }x\left| \phi _0(x,y)\right| ^2\textrm{d}x \textrm{d}y}{\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{+\infty } \left| \phi _0(x,y)\right| ^2\textrm{d}x\textrm{d}y} \end{aligned}$$

(38)

$$\begin{aligned} \eta _y&=\frac{\displaystyle \int _{-\infty }^{\infty } \int _{-\infty }^{+\infty }y\left| \phi _0(x,y)\right| ^2 \textrm{d}x\textrm{d}y}{\displaystyle \int _{-\infty }^{\infty } \int _{-\infty }^{+\infty } \left| \phi _0(x,y)\right| ^2\textrm{d}x\textrm{d}y} \end{aligned}$$

(39)

$$\begin{aligned} \xi _x&=\frac{\displaystyle \int _{-\infty }^{\infty } \int _{-\infty }^{+\infty }\frac{\partial \phi _0(x,y)}{\partial x} \phi _0^*(x,y)\textrm{d}x\textrm{d}y}{k\displaystyle \int _{-\infty }^{\infty } \int _{-\infty }^{+\infty }\left| \phi _0(x,y)\right| ^2\textrm{d}x\textrm{d}y} \end{aligned}$$

(40)

$$\begin{aligned} \xi _y&=\frac{\displaystyle \int _{-\infty }^{+\infty }\int _{-\infty }^{\infty } \frac{\partial \phi _0(x,y)}{\partial y}\phi _0^*(x,y) \textrm{d}x\textrm{d}y}{k\displaystyle \int _{-\infty }^{+\infty } \int _{-\infty }^{\infty }\left| \phi _0(x,y)\right| ^2\textrm{d}x\textrm{d}y} \end{aligned}$$

(41)

Using Eqs. (35) and (36), we can obtain the trajectory of the mass center

$$\begin{aligned} (\xi _y^2-P_0\gamma ^2\eta _y^2)x_c^2+(2P_0\gamma ^2\eta _x \eta _y-2\xi _x\xi _y)x_cy_c+(\xi _x^2-P_0\gamma ^2\eta _x^2) y_c^2=(\eta _y\xi _x-\eta _x\xi _y)^2 \end{aligned}$$

(42)