1 Introduction

With the increased demand of information bandwidth in optical communication systems to satisfy the internet needs, different multiplexing techniques have been proposed and used in the long-haul systems. This includes wavelength division multiplexing WDM, space division multiplexing SDM and polarization division multiplexing PDM (Dai and Bowers 2014). In space division multiplexing SDM, the optical power can be divided over different optical fiber cores or among the different modes of a few mode fiber (Richardson et al. 2013). When the power is divided over different modes, we have Mode Division multiplexing MDM in which each mode is modulated by an information channel to increase the capacity of the optical communication system (Memon and Chen 2021). This requires to differentiate between the different modes of the fiber at the receiver level and this differentiation is mainly based on the spatial distribution of the modes. Although the mode order is the main parameter that describes the field spatial distribution in the fiber, due to the fiber cylindrical symmetry, some modes could have the same mode order, i.e. same spatial distribution, while they have different orientation with respect to the X–Y domain. The typical example for this case is the LP11 mode (LP = Linearly Polarized) that has two peaks in the fiber cross section and these peaks could be distributed over the fiber X or Y axes and thus they are usually called the LP11a and LP11b modes (Yu et al. 2015). Transforming one of these modes to the other can be achieved by rotating the field 90 degree. This field rotator or mode converter is thus important for the realization of the integrated optical mode multiplexing.

Mode rotators have been proposed in the literature using different configurations (Yu et al. 2015; Saitoh et al. 2014; Wang et al. 2016; Yamashita et al. 2016; Zeng et al. 2016; Areez Khalil Memon 2021; Hong et al. 2016). In Saitoh et al. 2014, the authors proposed a waveguide with a trench to control the guide asymmetry and hence to rotate its LP11 modes by 45 degrees with respect to the X and Y directions. Exciting these two modes at the input and controlling the beating length between them allows the rotation of the input field by the required degree. A similar technique based on the generation of 2 modes with 45 degrees orientation with respect to the X and Y directions of the input field is reported in Wang et al. (2016), but in this proposal the mode rotation is created by a simple etching in the waveguide side. To reduce the insertion loss of such trench, the trench is curved in Yamashita et al. (2016) with respect to the propagation direction. The asymmetry can also be created through asymmetric heating as in Areez Khalil Memon (2021) and this allows the switching between the two states. The mode rotation can be also generated directly in the fiber either by twisting it (Yu et al. 2015), designing it with two inner cores (Zeng et al. 2016) or using a polarization maintaining fiber (Hong et al. 2016).

Although the optical mode rotator can be achieved by several technologies (Yu et al. 2015; Saitoh et al. 2014; Wang et al. 2016; Yamashita et al. 2016; Zeng et al. 2016; Areez Khalil Memon 2021; Hong et al. 2016), the Photonic Light wave Circuit (PLC) technology has the advantage of being quite compatible with the standard optical fiber technology and can be produced also on a Silicon substrate in mass production (Siew et al. 2021; Saitoh et al. 2017). It is based on a very week refractive index difference δn that is created by the slight difference in the 1.47288 core with respect to the 1.444 cladding. This results in a waveguide with dimensions very close to the fiber dimension and hence a very good power coupling can be achieved between the waveguide and the fiber. On the same time, this waveguide is still an integrated optical waveguide fabricated by planar technology on a Silicon substrate and thus can be fabricated in mass production with very low cost and can be integrated with other components to form a complete planar light wave circuit. On addition, a huge number of components have been proposed and tested on this technology as reported in Takahashi (2003); Mori et al. 2022; Hanzawa et al. 2013).

Recently, it was also possible to fabricate multilevel waveguides on this technology (Zhao et al. 2017, 2019; www.appliednt.com). The multilevel structure allows the fabrication of asymmetric directional coupler that can be used for mode division multiplexing (Wageeh et al. 2023; Elsabban and Khalil 2023). In this work, we present a nouvelle design for a field rotator using the multilevel PLC technology. The design is based on the use of an asymmetric directional coupler formed by two guides with different cross sections/orientation although they still have the same effective refractive index. This can be achieved easily in weakly guiding waveguides when using multilevel technology. The design will be explained in Sect. 2.

2 Design concept

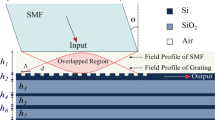
The objective of the design is a field rotator for the coupling between the LP11a and LP11b fiber modes shown in Fig. 1a and b respectively. To calculate these modes, we assume that we have a few mode fiber with a cladding refractive index of 1.444 and a core with diameter = 15.4 microns and created by δn = 0.00492. The two modes are identical except for their orientation as shown in Fig. 1. The basic idea in the design is the formation of an asymmetric directional coupler composed of two identical waveguides, one of them directed to the x direction and the second is rotated by 90 degree and directed to the Y direction as shown in Fig. 2. In this case when the power is coupled from the first order mode in guide 1 to the first order mode in guide 2, this coupling will be equivalent to the rotation of the field by an angle of 90 degree. In weakly guiding structures, these two guides are expected to have the same polarizations and effective refractive indices for their two first order modes and hence a 100% power coupling is expected within a short coupling length.

Fig. 1
figure 1

Field profile of the LP11a and LP11b modes of the fiber

Full size image
Fig. 2
figure 2

Asymmetric coupler structure for field rotation

Full size image

The analysis of such 2D coupling problem has been presented in reference (Wageeh et al. 2023). The advantage of such structure is its easy fabrication using the multilevel integrated optics technology. To demonstrate the idea, we consider the Silica over silicon low contrast technology. This technology allows to build waveguides with dimensions compatible with the single mode/few mode fiber dimensions and thus a very low coupling loss is expected. Thus, our waveguide will be composed of a cladding refractive index of N1 = 1.444 and a core with index N2 = N1 + δn with δn = 0.02888. The first guide has the dimensions of 19 µm × 15 µm while the second guide has the same dimensions in the opposite directions (order).i.e. 15 µm × 19 µm. Such waveguide can have a coupling efficiency with the fiber LP11 mode of 96.33%. As the dimensions of the two guides are fundamentally the same, it is expected to have the matching for the two guides over a wide spectral range, even when the material dispersion is taken into consideration. This similarity between the two guides allows the design also to be more immune to the temperature variations as it is expected to have similar changes in the refractive indexes in the two guides with temperature which is another advantage for this simple design. For the structure simulation, we use the 3D Beam Propagation Method BPM to calculate the required coupling length to achieve the complete power transfer between the two guides. For this purpose, the first order mode is launched in guide one (the horizontal guide) and the output field is monitored in guide 2 (the vertical guide). For such two guides, it is possible to get a complete power coupling (100% coupling efficiency) between the two guides after a coupling length of 89.860 mm ~ 9 cm, when the center to center separation between the two guides is 20 microns in the x direction and 6 microns in the y direction. Although this guiding structure clearly demonstrates the idea of our design, it results in a huge structure which is not compatible with the integrated optics technology. In the following we will demonstrate how to reduce the dimensions of the structure to get a more practical guiding structure based on the same concept.

3 Design optimization

From the above example we can see that the huge size of the structure results from the very large cross section of the waveguide to match the few mode fiber cross section. One way to overcome this problem is to use a special design for the fiber coupling that allows to use a waveguide with reduced dimensions and obtain a reasonable coupling efficiency in the same time. In the following we will examine two directions for this purpose.

3.1 Horizontal taper coupling

In this direction, we use a horizontal taper structure to reduce the waveguide width and reduce the guide depth. Using a horizontal taper, the waveguide width can be reduced from 19 to 6 µm to end with a waveguide with 15 µm × 6 µm. The design of such horizontal taper is a straight forward task that has been studied extensively in the literature (Duport et al. 1992). Thus, the coupler will be designed between two guides: a guide with 6 µm × 15 µm and another guide with the dimensions of 15 µm × 6 µm (width × depth). The choice of the 6 µm is motivated by the fact that it can still achieve a reasonable coupling with the few mode fiber through a short horizontal taper of length 240 mm as shown in Fig. 3. The taper has a length of only 240 µm. The field propagation through the taper from the fiber to the waveguide is shown in Fig. 3b. The coupling efficiency from the few mode fiber of diameter 15.4 µm to the waveguide of dimensions 15 µm × 19 µm is more than 95.5%. In this case the coupling length of the asymmetric coupler can be reduced. Table 1 shows the coupling length/coupling efficiency for different guide separations in both the X and Y directions. From Table 1 we can see that it is possible to achieve a very high coupling efficiency as high as 99.5% but with a lengthy coupler of around 11 mm length. On the other hand, if a lower coupling efficiency can be accepted for the coupler, we can get a coupling length of only 3.92 mm but in this case the coupling efficiency is around 88% only. However, the maximum depth on the wafer (Si layer thickness) is still 15 µm.

Fig. 3
figure 3

Horizontal taper connection between the few mode fiber and the guide of the coupler to reduce its dimensions

Full size image
Table 1 Coupling lengths (a) and coupling efficiencies (b) for asymmetric 2D coupler between the guides of 6 × 15 and 15 × 6 microns for different X and Y shifts.
Full size table

3.2 Y-junction coupling

For the sake of dimension reduction, it is possible to reduce the dimensions of the single waveguide used in the MAC coupler by using a special design for the coupling with the few mode fiber. This special design will be tailored for the LP11 mode shape. This can be done by using a Y-junction structure as shown in Fig. 4. This Y junction will be designed such that the centers of its two waveguides A & B in Fig. 4. (separated by the distance Δ) are aligned with the centers of the 2 peaks of the LP11 mode in the few mode fiber. Actually, these two guides A and B are acting as two inverted tapers to couple the two peaks of the LP11 mode (Mu et al. 2020; Ren et al. 2011). Each of them will thus have the dimensions of 1.5 µm × 1.8 µm. On the same time, the width of the output guide C is sufficient to support two guided modes. Thus, guide C will have the dimensions of 6 µm × 1.8 µm (same depth as A and B). This guide will be also the building block for the MAC coupler, i.e. the MAC coupler will be composed of two guides, one with 6 µm × 1.8 µm and the second with 1.8 µm × 6 µm which reduced greatly the maximum depth used in the structure. This also leads to a reduction in the length of the coupler. The properties of this MAC coupler will be analyzed in the next section.

Fig. 4
figure 4

Y junction with 2 inverted tapers for the coupling of the LP11 mode into waveguide C

Full size image

3.3 MAC coupler design

The design of the reduced dimensions MAC coupler formed by guide C and its rotated version are studied in this section. The study of the structure will be based on both the Coupled Mode Theory (CMT) and the Numerical BPM calculations. From the Coupled mode theory, we may consider that the field propagating in one guide is the source for the excitation of the field to propagate in the second guide. Thus, when the coupling is weak, we may consider this field as a perturbation to the solution in the second guide and consequently, the solution in the second guide can still be expressed as a sum of the modes of the unperturbed guide. This allows expressing the field evolution with the propagation distance in the guide as a function of the overlap between the tail of the exciting field and the perturbed waveguide. Solving such field evolution equations, we can express the field evolution of transfer between the two guides as a periodic function characterized by a coupling coefficient k12 that express the periodicity in length of the power transfer between the two coupled guides. Following the detailed analysis in Huang (1994); Okamoto 2006), the coupling coefficient between mode 1 in the first guide with Electric field distribution E1 and magnetic field distribution H1 and mode 2 in guide 2 with electric field distribution E2 and magnetic field distribution H2 can be expressed by:

$$k_{12} = \frac{{\omega \varepsilon_{0} \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {N^{2} - N_{2}^{2} } \right)E_{1}^{*} \cdot E_{2} dydx} } }}{{\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {a_{z} \cdot \left( {E_{1}^{*} {\text{x}}H_{{1}} + E_{{1}} {\text{x}}H_{1}^{*} } \right)dydx} } }}$$
(1)

where N represents the refractive index distribution in the overall waveguide, and N2 represents the refractive index distribution in guide 2 only, ω is the operating angular frequency of the optical signal, εo is the free permittivity and az is the unit vector perpendicular to the cross-section area of the waveguides. While the denominator represents the normalization integral of the field in guide 1, the nominator depends mainly on the dot product of the two field vectors of the two modes. The coupling length can then be evaluated through the relation:

$${L}_{c}=\frac{\pi }{2{k}_{12}}$$
(2)

where the two modes are assumed to have the same propagation constants. Equations 1 and 2 show that the coupling length of the coupler depends essentially on the overlap between the two modes of the two guides. This overlap is mainly determined by the separations between the two guides in both the x and y directions. To calculate the coupling length using the coupled mode theory, we calculate the mode in each guide and then evaluate numerically the integration in Eq. 1 taking into account both the Y shift and the X shift (separation) between the two guides.

Figure 5 shows the variation in the coupling length as a function of the horizontal separation between the two guides for 2 vertical separations (Y shifts), 6 microns and 7 microns. The calculation is done using both the Coupled mode theory CMT (dotted lines) and the 3D Beam Propagation Method 3DBPM (solid lines). The scalar version is used for both of them due to the weakly guiding conditions. The results of the two techniques are in good agreement. For the BPM calculations, the parameters shown in Table 2 have been used.

Fig. 5
figure 5

Coupling length of the compact MAC composed of two waveguides with dimensions 6 µm × 1.8 µm as a function of the horizontal separation between the two guides (X-shift) for different y shifts

Full size image
Table 2 The parameters used in BPM calculations
Full size table

It is clear that the reduction of the separation (in the X or Y directions) between the two guides (x-shift or Y-shift) reduces the length required for achieving the power coupling as expected from the coupled mode theory. However, reducing the separation between the two guides (at very small separations) results also in an increase in the overlap between the two modes of the two waveguides and thus even when there is a complete power transfer from guide 1 to guide 2, there will be still a strong overlap with the guided mode of guide 1 and hence the coupling efficiency is affected. Figure 6 shows the coupling efficiency between the 2 guides as a function of the horizontal shift between the two guides for different vertical separations/shifts. For a better coupling efficiency, it is required to increase the separation between the two guides and hence increase the coupling length. Thus, in the design of the coupler, there is a compromise between the coupling efficiency and the footprint of the coupler. This can also be observed in Fig. 7 where the coupling efficiency and the coupling lengths are calculated as a function of the Y shift for an x-shift between the two couplers = 6 microns. Two points are of interest in this curve: when the bottom layers of the two guides are aligned and when the top of one guide is aligned with the bottom of the second guide. The importance of these two points is that at these points the MAC coupler will have only three layers in the fabrication process instead of 4 layers and hence a lower number of masks and a lower cost. We also observe a good agreement between the coupled mode theory calculations and the BPM results. In addition, we note that the coupling length has also the tendency to increase as the Y shift is reduced. This is expected as for a Y shift = 0, we get two modes one with even symmetry and the other with odd symmetry with respect to the Y axis and thus from the CMT, the coupling length at that point should again tend to infinity as expected in Wageeh et al. (2023).

Fig. 6
figure 6

Coupling efficiency of the compact MAC studied in “Fig. 5” as a function of the horizontal separation/shift between the two guides for different y shifts

Full size image
Fig. 7
figure 7

Coupling efficiency and coupling length for the MAC coupler as a function of the Y shift for an X shift of 6 microns

Full size image

3.4 Design of the overall rotator

The complete structure used for achieving the field rotation is shown in Fig. 8. The structure is composed of an input inverted horizontal taper to couple the power from the input LP11b mode of the few mode fiber. The inverted taper has input dimensions of 1.5 µm (width) × 6 µm (depth) and ends with a guide of 1.8 µm (width) × 6 µm (depth). This guide is then coupled to another guide of 6 µm (width) × 1.8 µm (depth) through evanescent coupling to form the MAC coupler and is used to rotate the field by 90 degrees. The guide of 6 µm (width) × 1.8 µm (depth) is then coupled to the few mode fiber using a Y junction that ends by two inverted tapers with tips of dimensions 1.5 µm (width) × 1.8 µm (depth) to excite the LP11a mode of the few mode fiber efficiently.

Fig. 8
figure 8

Field propagation in the proposed overall field rotator. The input LP11b mode from a few mode fiber is coupled to the silica/silicon waveguide through an inverted taper, a MAC coupler is used to rotate the field by 90 degree and then a Y junction is used to couple the output field to the LP11a mode of the few mode fiber. The overall fiber to fiber coupling efficiency of the proposed structure is around 57%

Full size image

The overall fiber to fiber coupling efficiency of the proposed structure is around 57% and its overall length is less than 2 mm. The coupling efficiency of the MAC coupler is around 91% and the rest is due to the coupling with the fiber at the two ends of the structure.

The details of the structure power budget and the coupling efficiencies of the different elements are as follows:

  1. 1

    The fiber coupling to the input guide of width 1800 nm and depth 6 microns through an inverted taper of length 557 microns has an efficiency of 77.5%

  2. 2

    The output fiber coupling to the guide of width 6 microns and depth of 1800 nm through two inverted tapers of length 500 microns and a Y junction has an efficiency of 81.2%

  3. 3

    Multilayer coupler has a coupling efficiency of about 91% for a length of 550 microns

This gives an overall fiber to fiber coupling of 57% which is less than 3 dB insertion loss. It is clear that the lowest coupling efficiency is that with the waveguide of depth 6 microns at the input. To improve this efficiency, it is required to increase the depth of the structure and we believe that this might increase greatly its cost. The relatively low coupling results from the use of a fiber with large core area (diameter of 15.4 micros) which is a typical few mode fiber.

The field propagation in the structure, calculated using the 3D BPM is shown in Fig. 8, in addition with an illustration of the 2D field profile at some selected cross sections. These cross sections illustrate how the field is rotated in the space using the evanescent coupling to form the required output mode. The wavelength dependence of the structure is also calculated using the BPM and illustrated in Fig. 9. It shows a 3 dB bandwidth of about 360 nm around the operating wavelength of 1550 nm.

Fig. 9
figure 9

Wavelength response of the proposed field rotator formed by an asymmetric coupler between the two guides of 1.8 × 6 microns with a vertical Y-shift of 2.1 microns and a horizontal x-shift of 6 microns and a coupler length of 550 microns (an ADC with a coupling efficiency of about 91%) and an overall field rotator with a coupling efficiency of 57% at the wavelength of 1550 nm

Full size image

It is to be noted here that the same idea can also be used for any guiding structure, i.e. for other material compositions as the only difference between the two guides is the orientations. However, for strong guiding (high index contrast) waveguides, the polarization of the optical fields in the two guides should be taken into consideration as the coupling between the two guides depends also on the field polarization. If there is an angle between the two coupled modes in the two guides, this angle is expected to increase the coupling length as the coupling coefficient is simply multiplied by the cosine of this angle as indicated in the dot product in Eq. 1 and hence the coupling length will increase by a factor of 1/cos(θ), where θ is the angle between the electric fields of the two coupled modes. Also, for other fiber geometries, the coupling with the input/output fiber mode, may need special optimization to match the fiber dimensions without increasing the waveguide height dramatically to facilitate the structure fabrication.

The parameters of proposed design can be summarized in the Table 3. We note that, as the waveguide has a depth of 1.8 microns, the waveguide center is located at the height of 0.9 microns and the second guide has a depth of 6 microns and width of 1.8 microns. Thus when the Y-shift is 2.1 microns we have the bottom lines of the two guides perfectly aligned and this means we have only 3 layers for the Silicon etching in the fabrication process. This results in lower number of masks and lower process steps which allows lower fabrication cost. On the other hand, using an x-shift of 6 microns allows getting a high conversion efficiency in the coupler with reasonable footprint as shown in Fig. 5.

Table 3 The parameters of the design
Full size table

The proposed structure shows that we can build a field rotator based on the use of an asymmetric directional coupler using the multilevel silicon technology. This allows to build the rotator with different geometries following the required specifications. If we consider the example given above, we see that we could have a rotator with a coupling efficiency greater than 99% with 1 mm length. However, we can also (by simply adjusting the Y shift and X shift of the couplers) reduce the size to 0.55 mm if we accept the coupling efficiency to be only 91%. This flexibility in the design makes this solution quite suitable for different applications. Another important advantage for this design is that it uses simple technology that is now available in many photonics factories, and it does not need special technological development.

4 Conclusion

This work demonstrates a Multilevel Asymmetric Coupler MAC field rotator for the LP11 mode using the Silica over Silicon technology. The rotator is using a waveguide asymmetric coupler with a coupling efficiency of 91%. Using Y junction and inverted tapers for the coupling with a few mode fiber of diameter 15.4 microns, the proposed structure has an overall length less than 2 mm and shows an overall fiber to fiber insertion loss less than 3 dB (about 57% coupling), and a 3DB bandwidth of 360 nm around the wavelength of 1550 nm. The design of the MAC coupler shows that there is a compromise between the coupling efficiency and the footprint on the die.