Investigation of travelling wave solutions for the (3 + 1)-dimensional hyperbolic nonlinear Schrödinger equation using Riccati equation and F-expansion techniques

Abstract

The (3 + 1)-dimensional hyperbolic nonlinear Schrödinger equation (HNLS) is used as a model for different physical phenomena such as the propagation of electromagnetic fields, the dynamics of optical soliton promulgation, and the evolution of the water wave surface. In this paper, new and different exact solutions for the (3 + 1)-dimensional HNLS equation is emerged by using two powerful methods named the Riccati equation method and the F-expansion principle. The behaviors of resulting solutions are different and expressed by dark, bright, singular, and periodic solutions. The physical explanations for the obtained solutions are examined by a graphical representation in 3d profile plots.

1 Introduction

Many modern phenomena in physics, biology, chemistry, engineering, plasma, optics, and many others may be modeled with nonlinear evolution equations (NLEE's). A better understanding of these phenomena is the focus and interest of many researchers in this field, and therefore great interest was in obtaining exact solutions for these models. Inspired by the last observation, many analytical and numerical methods have emerged for this, despite this, there is no specific method to obtain exact solutions for all models, as the method that is effective in one model is ineffective in another one, these methods including inverse scattering transform method (Ali et al. 2022; Ali et al. 2023), Darboux transformation (Monisha et al. 2022), Bäcklund transformation (Dong et al. 2022), the hyperbola function method (Bai 2001), the sine–Gordon expansion method (Kundu, et al. 2021), the improved Bernoulli sub-equation function method (Islam and Ali Akbar 2020; Islam et al. 2020), the lumped Galerkin method (Esen 2005), the Jacobi elliptic function method (Tian 2017), sine–cosine method (Wazwaz 2006), tanh-sech method (Seadawy 2014; Aly 2014), extended tanh-coth method (Bekir 2009), Lie group symmetry analysis method (Sadat et al. 2021; Dig Vijay Tanwar 2022), the first integral method (El-Ganaini 2013), modified extended mapping method (Bai et al. 2011), homogeneous balance method (Aly 2016; Zayed and Arnous 2012), the exp-function method (Remarks and on Exp-Function Method and Its Applications-A Supplement 2013), modified simple-equation method (Irshad et al. 2017; Ali et al. 2017), Kudryashov method (Aly 2017a; Kumar et al. 2018; Barman, et al. 2021), F-expansion method (Zhou et al. 2003; Yıldırım et al. 2020; Yıldırım and Mirzazadeh 2020), Riccati equation method (Bekir 2009; Yıldırım et al. 2020; Yıldırım and Mirzazadeh 2020; Huang and Zhang 2005; Song et al. 2007; El-Ganaini and Kumar 2020) and many others.

The nonlinear Schrödinger equation (NLS) is one of the most important NLEE's which shows its importance in many applications such as optical fibers communications, Heisenberg spin chain, plasma, applied and theoretical physics and many others (El-Ganaini 2013; Li 2007; Gorza 2008; Efremidis et al. 2009; Saha et al. 2009; Ai-Lin and Ji 2010; Triki and Biswas 2011; Guo and Lin 2012; Triki et al. 2012; Ahmed et al. 2014; Zayed 2016; Arshad et al. 2017; Aly 2017b; Mohamed 2018; Seadawy et al. 2018; Islam et al. 2022a, 2022b, 2022c, 2022d, 2022e, 2023; Akbar et al. 2023; Abdullah et al. 2023). The NLS equation takes many forms, among them is the hyperbolic nonlinear Schrödinger (HNLS) equation which the (2 + 1)-dimensional form is given by

$$i{\psi }_{y}+\frac{1}{2}\left({\psi }_{xx}-{\psi }_{tt}\right)+{\psi }^{2}{\psi }^{*}=0,$$

(1)

where $\psi =\psi (x,y,t)$ denote a complex field, $x$ and $y$ are the spatial coordinates and $t$ is the temporal variable. Equation (1) is used in two important applications, the first one is the description of the dynamics of optical soliton promulgation in monomode optical fibers, while the second one is the description of the evolution of the elevation of water wave surface for slowly modulated wave trains in deep water in hydrodynamics. The exact travelling wave solutions for Eq. (1) have been obtained in different contexts by using different powerful methods (Li 2007; Efremidis et al. 2009; Ai-Lin and Ji 2010; Guo and Lin 2012; Ahmed et al. 2014; Zayed 2016; Mohamed 2018; Islam et al. 2022a, 2022b, 2022c, 2023).

In the present article, we aim to study the extension of the HNLS equation in three dimensions namely (3 + 1)-dimensional hyperbolic non-linear Schrödinger (HNLS) equation which is given by Abdullah et al. (2023)

$$i{\psi }_{y}+\frac{1}{2}\left({\psi }_{xx}+{\psi }_{zz}-{\psi }_{tt}\right)+{\psi }^{2}{\psi }^{*}=0,$$

(2)

where $\psi =\psi (x,y,z,t)$ is a complex- valued function, ${\psi }^{*}$ is the complex conjugate of $\psi$, $i=\sqrt{-1}$, while $x,y$ and $z$ are the spatial variables and $t$ stands for the temporal variable. In the study, we will use two powerful methods, namely Riccati equation technique and F-expansion principle (Yıldırım and Mirzazadeh 2020) to obtain different travelling wave solutions Eq. (2). It is worth noting that, the HNLS (2) has appeared in many different applications, such that, it is used as a model for different physical phenomena such as the propagation of electromagnetic fields, the dynamics of optical soliton promulgation and the evolution of the water wave surface. In the literature, the exact travelling wave solutions for Eq. (2) have been also obtained, such that, in Abdullah et al. (2023) a set of different exact solutions namely, bright, dark, complex, singular and periodic solutions have been obtained.

The rest of the present article is organized as follows: in Sect. 2, a quick review of the Riccati equation technique and its steps followed by different exact travelling wave solutions to Eq. (2) will be illustrated. The instructions of the F-expansion principle and the usage of it as an application to Eq. (2) are shown in Sect. 3. In Sect. 4, the physical explanation of the obtained solutions is examined with 3d profile plots representation. The conclusion of our work is summarized in Sect. 5.

2 Riccati equation technique

In this section, we briefly review the main steps that we take to obtain exact travelling wave solutions for any NLEE in general and apply them to HNLS Eq. (2).

2.1 A quick review of Riccati equation technique

Consider a general governing model given as a NLEE in two independent variables $x$ and $t$ (which may be extended to more than two independent variables) is written as

$$P\left(\psi ,{\psi }_{t},{\psi }_{x},{\psi }_{tt},{\psi }_{xx},\dots \right)=0,$$

(3)

where $P$ and $\psi$ are unknown's functions that have linear and nonlinear derivatives of higher order. The main procedures of the standard Riccati equation technique can be summarized as follows.

Step (1): The given nonlinear evolution Eq. (3) is transformed into an equation of a single variable by using the following travelling wave transformation

$$\psi \left(x,t\right)=U\left(\xi \right), \, \xi =kx+wt.$$

(4)

where $k$ is the wavelength and $w$ is the frequency. Through Eq. (4), the NLEE (3) is transformed into a nonlinear ordinary differential equation (NODE)

$$F\left(U,{U}^{\prime},{U}^{{\prime}{\prime}},{U}^{{\prime}{\prime}{\prime}},\dots \right)=0,$$

(5)

Step (2): Suppose that the solution structure of Eq. (5) can be written as

$$U\left(\xi \right)=\sum_{j=0}^{N}{A}_{j}{\phi }^{j}\left(\xi \right),$$

(6)

where ${A}_{j}$ are real constants, $N$ is a positive integer which results via the balancing principle with higher order non-linear and linear terms in Eq. (5) and $\phi \left(\xi \right)$ satisfies the Riccati equation in the form

$${\phi }{\prime}\left(\xi \right)=a{\phi }^{2}\left(\xi \right)+b\phi +c,$$

(7)

where $a\ne 0, b$ and $c$ will be determined.

Step (3): Inserting Eq. (6) together with Eq. (7) into Eq. (5) and equating the coefficients of ${\phi }^{j}$, $j=\mathrm{0,1},\dots ,N$ to zero, one can obtain a system of equations in the series of unknowns parameters $k,w,{A}_{i},a,b$ and $c$ which can be solved via MATHEMATICA or MAPLE software.

Step (4): Putting the obtained values of parameters from the procedure (3) into Eq. (5) through which the travelling wave solution can also be obtained using Eq. (4).

We note that the Riccati Eq. (7) is a non-linear first order ODE that can be solved via the separation of variables. Suppose that

$$\beta ={b}^{2}-4ac,$$

(8)

Then depending on $\beta$, the solutions of Eq. (7) can be written as follows.

Case (1): $\beta >0,$

Case (1–1): $\left|2a\phi +b/\sqrt{\beta }\right|>1,$

$$\phi \left(\xi \right)=-\frac{b}{2a}-\frac{\sqrt{\beta }}{2a}\mathrm{tanh}\left(\frac{\sqrt{\beta }}{2}\xi +{\xi }_{0}\right),$$

(9)

Case (1–2): $\left|2a\phi +b/\sqrt{\beta }\right|<1,$

$$\phi \left(\xi \right)=-\frac{b}{2a}-\frac{\sqrt{\beta }}{2a}\mathrm{coth}\left(\frac{\sqrt{\beta }}{2}\xi +{\xi }_{0}\right),$$

(10)

Case (2): $\beta <0,$

$$\phi \left(\xi \right)=-\frac{b}{2a}+\frac{\sqrt{-\beta }}{2a}\mathrm{tan}\left(\frac{\sqrt{-\beta }}{2}\xi +{\xi }_{0}\right),$$

(11)

$$\phi \left(\xi \right)=-\frac{b}{2a}-\frac{\sqrt{-\beta }}{2a}\mathrm{cot}\left(\frac{\sqrt{-\beta }}{2}\xi +{\xi }_{0}\right).$$

(12)

Case (3): $\beta =0,$

$$\phi \left(\xi \right)=-\frac{b}{2a}-\frac{1}{a\xi +{\xi }_{0}},$$

(13)

Where ${\xi }_{0}$ is the integration arbitrary constant.

2.2 Travelling wave solutions via Riccati equation technique

In this subsection, we obtain different soliton solutions for HNLS Eq. (2) by considering the Riccati equation method. First, apply the following travelling wave transformation to HNLS Eq. (2)

$$\psi \left(x,y,z,t\right)=U\left(\xi \right){e}^{i\varphi (x,y,z,t)},$$

(14)

where

$$\xi \left(x,y,z,t\right)=\eta \left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right),$$

(15)

$$\varphi \left(x,y,z,t\right)=-{k}_{1}x-{k}_{2}y-{k}_{3}z+wt,$$

(16)

From Eqs. (2) and (14), we obtain the following derivatives

$$ \begin{aligned} i\psi_{y} = & \left( {k_{2} U + i\eta B_{2} U^{\prime}} \right)e^{i\varphi } , \\ \frac{1}{2}\psi_{xx} = & \left( { - \frac{1}{2}k_{1}^{2} U - ik_{1} \eta B_{1} U^{\prime} + \frac{1}{2}\eta^{2} B_{1}^{2} U^{\prime\prime}} \right)e^{i\varphi } , \\ \frac{1}{2}\psi_{zz} = & \left( { - \frac{1}{2}k_{3}^{2} U - ik_{3} \eta B_{3} U^{\prime} + \frac{1}{2}\eta^{2} B_{3}^{2} U^{\prime\prime}} \right)e^{i\varphi } , \\ \frac{1}{2}\psi_{tt} = & \left( {\frac{1}{2}\eta^{2} - \frac{1}{2}w^{2} U - iw\eta \rho U^{\prime}} \right)e^{i\varphi } , \\ \psi^{2} \psi^{*} = & U^{3} e^{i\varphi } . \\ \end{aligned} $$

(17)

Inserting the obtained results from Eq. (17) into Eq. (2), then Eq. (2) is then converted to non-linear ODE which can be written in the following real and imaginary parts.

The real part:

$$\left({\eta }^{2}{B}_{1}^{2}+{\eta }^{2}{B}_{3}^{2}-{\eta }^{2}{\rho }^{2}\right){U}^{{\prime}{\prime}}+\left(2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}\right)U+2{U}^{3}=0,$$

(18)

The imaginary part:

$$\rho w-{k}_{1}{B}_{1}-{k}_{3}{B}_{3}+{B}_{2}=0,$$

(19)

Using Eq. (18) and assuming that it's solution can be written as

$$U\left(\xi \right)=\sum_{j=0}^{N}{A}_{j}{\phi }^{j}\left(\xi \right),$$

(20)

where ${A}_{j}$ are real constant will be determined and $\phi (\xi )$ satisfies the Riccati Eq. (7).

According to the balancing principle and from Eq. (18) we conclude that $N=1$ and hence the series in Eq. (20) can be expanded as

$$U={A}_{0}+{A}_{1}\phi ,$$

(21)

From Eq. (21) together with Eq. (7) we obtain the following formulas for ${U}^{\prime}, U^{\prime\prime}$ and ${U}^{3}$

$$ \begin{aligned} U^{\prime\prime} =\, & 2a^{2} A_{1} \phi^{3} + 3abA_{1} \phi^{2} + \left( {2acA_{1} + b^{2} A_{1} } \right)\phi + bcA_{1} , \\ U^{3} =\, & A_{1}^{3} \phi^{3} + 3A_{0} A_{1}^{2} \phi^{2} + 3A_{0}^{2} A_{1} \phi + A_{0}^{3} , \\ \end{aligned} $$

(22)

Inserting the obtained results from Eq. (22) into Eq. (18) and equating the coefficients of different exponents of $\phi$ to zero, we obtain the following system of equations

$$ \begin{gathered} \left( {2a^{2} A_{1} } \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + 2A_{1}^{3} = 0, \hfill \\ \left( {3abA_{1} } \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + 6A_{0} A_{1}^{2} = 0, \hfill \\ \left( {2acA_{1} + b^{2} A_{1} } \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + A_{1} \left( {2k_{2} - k_{1}^{2} - k_{3}^{2} + w^{2} } \right) + 6A_{0}^{2} A_{1} = 0, \hfill \\ \left( {bcA_{1} } \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + A_{0} \left( {2k_{2} - k_{1}^{2} - k_{3}^{2} + w^{2} } \right) + 2A_{0}^{3} = 0. \hfill \\ \end{gathered} $$

(23)

Using MAPEL software to solve the system in Eq. (23), we obtain the following important results for $a, b$ and $c$

$$a=\pm \frac{{A}_{1}}{\eta \sqrt{{\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}}},$$

(24)

$$b=\pm \frac{2{A}_{0}}{\eta \sqrt{{\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}}},$$

(25)

$$c=\pm \frac{2{A}_{0}^{2}+{w}^{2}-{k}_{1}^{2}-{k}_{3}^{2}+2{k}_{2}}{2{A}_{1}\eta \sqrt{{\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}}}.$$

(26)

From Eqs. (24–26) and using Eq. (8) we have

$$\beta =-\frac{2\left({w}^{2}-{k}_{1}^{2}-{k}_{3}^{2}+2{k}_{2}\right)}{\left({\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}\right){\eta }^{2}}.$$

(27)

Inserting Eqs. (24–27) into Eqs. (9–13) and by using Eqs. (21, 14), the travelling wave solutions for HNLS Eq. (2) will be obtained as follows.

Case (1): when $\beta >0$ (see Eq. (27)), we obtain the following travelling wave solutions.

Case (1–1): Dark optical soliton solution

$${\psi }_{1}\left(x,y,z,t\right)=\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2}}\mathrm{tanh}\left(\left(\rho t-{B}_{1}x-{B}_{2}y-{B}_{3}z\right)\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2\left({\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}\right)}}+{\xi }_{0}\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(28)

Case (1–2): Singular soliton solution

$${\psi }_{2}\left(x,y,z,t\right)=\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2}}\mathrm{coth}\left(\left(\rho t-{B}_{1}x-{B}_{2}y-{B}_{3}z\right)\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2\left({\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}\right)}}+{\xi }_{0}\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(29)

Case (2): when $\beta <0$ (see Eq. (27)), we obtain the following singular periodic soliton solutions

$${\psi }_{3}\left(x,y,z,t\right)=\pm \sqrt{\frac{-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}+2{k}_{2}}{2}}\mathrm{tan}\left(\left(\rho t-{B}_{1}x-{B}_{2}y-{B}_{3}z\right)\sqrt{\frac{-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}+2{k}_{2}}{2\left({\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}\right)}}+{\xi }_{0}\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}$$

(30)

$${\psi }_{4}\left(x,y,z,t\right)=\pm \sqrt{\frac{-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}+2{k}_{2}}{2}}\mathrm{cot}\left(\left(\rho t-{B}_{1}x-{B}_{2}y-{B}_{3}z\right)\sqrt{\frac{-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}+2{k}_{2}}{2\left({\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}\right)}}+{\xi }_{0}\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}$$

(31)

where $\rho$ is defined in Eq. (19).

3 F-expansion principle

In this section, similarly, as in the previous sections, we will initially review the steps followed in.

F-expansion method to obtain exact soliton solutions of NLEE's and follow them to obtain exact soliton solutions of HNLS Eq. (2).

3.1 A quick review of F-expansion principle

Consider a general NLEE in two independent variables $x$ and $t$ (which may be extended to more than two independent variables) is written as

$$P\left(\psi ,{\psi }_{t},{\psi }_{x},{\psi }_{tt},{\psi }_{xx},\dots \right)=0$$

(32)

where $P$ and $\psi$ are unknowns' functions that have linear and nonlinear derivatives of higher order. The main procedures of the standard F-expansion principle can be summarized as follows.

Step 1: The given nonlinear evolution Eq. (32) is transformed into an equation of a single variable by using the following travelling wave transformation

$$\psi \left(x,t\right)=U\left(\xi \right), \xi =kx+wt$$

(33)

where $k$ is the wavelength and $w$ is the frequency. Through Eq. (33), the NLEE (32) is transformed to a nonlinear ordinary differential equation (NODE)

$$F\left(U,{U}{\prime},{U}^{{\prime}{\prime}},{U}^{{\prime}{\prime}{\prime}},\dots \right)=0,$$

(34)

Step 2: Suppose that the solution structure of Eq. (34) can be written as

$$U\left(\xi \right)=\sum_{j=0}^{N}{s}_{j}{F}^{j}\left(\xi \right),$$

(35)

where ${s}_{j}$ are real constants, $N$ is positive integer which result via the balancing principle with higher order non-linear and linear terms in Eq. (34) and $\phi \left(\xi \right)$ satisfies the following first order ODE

$${F}{\prime}\left(\xi \right)=\sqrt{P{F}^{4}\left(\xi \right)+Q{F}^{2}+R.}$$

(36)

where $T\ne 0, Q$ and $R$ will be determined.

Step 3: Inserting Eq. (35) together with Eq. (36) into Eq. (34) and equating the coefficients of.

${F}^{j}$, $j=\mathrm{0,1},\dots ,N$ to zero, one can obtain a system of equations in the unknowns parameters $k,w,{s}_{i},P,Q$ and $R$ which can be solved via MATHEMATICA or MAPLE software.

Step 4: Putting the obtained values of parameters from procedure (3) into Eq. (34) through which the travelling wave solution can also be obtained using Eq. (33).

We note that, in Table 1, the solutions of Eq. (36) are illustrated in terms of Jacobian elliptic functions, for more details we recommended (Akram et al. 2023).

Table 1 Solutions of Eq. (36) in terms of Jacobian elliptic functions

3.2 Travelling wave solutions via F-expansion principle

In this subsection, by following the steps mentioned in the F-expansion method in the previous section, we begin by applying the travelling wave transformation in Eq. (14) to HNLS Eq. (2), then Eq. (2) is converted to a nonlinear ODE which it's real and imaginary parts are written in Eqs. (18) and (19), respectively. Using Eq. (18) and assuming that it's solution can be written as

$$U\left(\xi \right)=\sum_{j=0}^{N}{s}_{j}{F}^{j}\left(\xi \right),$$

(37)

where ${s}_{j}$ are real constant will be determined and $F(\xi )$ satisfies Eq. (36).

According to the balancing principle, then from Eq. (18) we conclude that $N=1$ and hence the series in Eq. (37) can be expanded as

$$U={s}_{0}+{s}_{1}F,$$

(38)

From Eq. (38) together with Eq. (36) we obtain the following formulas

$$ \begin{aligned} U^{\prime\prime} = &\, 2s_{1} PF^{3} + s_{1} QF, \\ U^{3} = &\, s_{1}^{3} F^{3} + 3s_{0} s_{1}^{2} F^{2} + 3s_{0}^{2} s_{1} F + s_{0}^{3} , \\ \end{aligned} $$

(39)

Using Eq. (39) together with Eq. (18) and equating the different exponent of ${F}^{j}, j=\mathrm{0,1},\mathrm{2,3}$ to zero, we obtain the following system of equations

$$ \begin{gathered} \left( {s_{1} Q} \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + s_{1} \left( {2k_{2} - k_{1}^{2} - k_{3}^{2} + w^{2} } \right) + 6s_{0}^{2} s_{1} = 0, \hfill \\ \left( {2s_{1} P} \right)\left( {\eta^{2} B_{1}^{2} + \eta^{2} B_{3}^{2} - \eta^{2} \rho^{2} } \right) + 2s_{1}^{3} = 0, \hfill \\ s_{0} \left( {2k_{2} - k_{1}^{2} - k_{3}^{2} + w^{2} } \right) + 2s_{0}^{3} = 0,6s_{0} s_{1}^{2} = 0. \hfill \\ \end{gathered} $$

(40)

The solution of system (40) using MAPLE software gives.

$${s}_{0}=0, {s}_{1}=\pm \sqrt{\frac{P\left(2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}\right)}{Q}}, \eta =\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{Q\left({B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}\right)}}.$$

(41)

Inserting the obtained values from Eq. (41) into Eq. (38) and using Table 1, the travelling wave solutions for HNLS in Eq. (2) are obtained as follows.

Case (1): Dark-soliton solution

$${\psi }_{5}=\pm \sqrt{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}tanh\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{{\rho }^{2}-{B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(42)

Case (2): Bright-soliton solution

$${\psi }_{6}=\pm \sqrt{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}sech\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(43)

Case (3): Singular-soliton solutions

$${\psi }_{7}=\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}{2}}coth\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2\left({{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}\right)}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(44)

$${\psi }_{8}=\pm \sqrt{2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}}csch\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.$$

(45)

Case (4): Singular-periodic soliton solutions

$${\psi }_{9}=\pm \sqrt{\frac{2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}}{2}}tan\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2\left({B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}\right)}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(46)

$${\psi }_{10}=\pm \sqrt{\frac{2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}}{2}}cot\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{2\left({B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}\right)}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(47)

$${\psi }_{11}=\pm \sqrt{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}csc\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)},$$

(48)

$${\psi }_{12}=\pm \sqrt{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}sec\left(\sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2}}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right){e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.$$

(49)

Case (5): Cluster-singular soliton solution

$${\psi }_{13}=\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}{2}}\left[coth\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\pm \, csch\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\right]{e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.$$

(50)

Case (6): Dark-bright soliton solution

$$\begin{aligned}{\psi }_{14} & =\pm \sqrt{\frac{{k}_{1}^{2}+{k}_{3}^{2}-2{k}_{2}-{w}^{2}}{2}}\left[tanh\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\right. \\ & \quad \left. \pm \, sech \left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{{\rho }^{2}-B}_{1}^{2}-{B}_{3}^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\right]{e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.\end{aligned}.$$

(51)

Case (7): Cluster-singular periodic soliton solutions

$${\psi }_{15}=\pm \sqrt{\frac{2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}}{2}}\left[csc\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\pm \, cot\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\right]{e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.$$

(52)

$${\psi }_{16}=\pm \sqrt{\frac{2{k}_{2}-{k}_{1}^{2}-{k}_{3}^{2}+{w}^{2}}{2}}\left[sec\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\pm \, tan\left(\sqrt{\frac{2({k}_{1}^{2}+{k}_{3}^{2}-{w}^{2}-2{k}_{2})}{{B}_{1}^{2}+{B}_{3}^{2}-{\rho }^{2}}}\left({B}_{1}x+{B}_{2}y+{B}_{3}z-\rho t\right)\right)\right]{e}^{i\left(wt-{k}_{1}x-{k}_{2}y-{k}_{3}z\right)}.$$

(53)

where $\rho$ is defined in Eq. (19).

4 Results, physical examination, and discussion

In this section, we will illustrate graphically some solutions for the obtained general ones in the previous section. These solutions are coming from giving the arbitrary parameters ${k}_{1}, {k}_{2}, {k}_{3}, {B}_{1}, {B}_{2}, {B}_{3}$ and $w$ a special value.

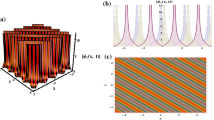
Figure 1 shows the solution structure for soliton solutions was obtained by Riccati equation method. Figure 1a shows the dark-soliton solution ${\psi }_{1}$ with parameters values

Fig. 1

The solution structure for soliton solutions obtained by Riccati equation technique

B₁ = 0.8, B₂ = 0.6, B₃ = 1, k₁ = 0.5, k₂ = k₃=1, w =1.3, η = 1, ξ₀ = 0, y = −2, z = 1.

Figure (1-b) illustrates the singular soliton solution ${\psi }_{2}$ with

B₁ = 2, B₂ = 1, B₃ = 2, k₁ = 0.5, k₂ = k₃ = 1, w = 1, η = 1, ξ₀ = 0, y = 1, z = −2.

In Fig. 1c, the singular periodic soliton solution ${\psi }_{3}$ is shown with parameters values

B₁ = 1, B₂ = 2, B₃=2, k₁ = 1, k₂ = −0.7, k₃ = 1, w = 1, η = 1, ξ₀ = 0, y = 2, z = −4,

While in Fig. 1d, the singular periodic soliton solution ${\psi }_{4}$ is shown with parameters values

$$ B_{1} = B_{2} = B_{3} = - 1,{ }k_{1} = 1,{ }k_{2} = - 0.8,{ }k_{3} = 1.4,{ }w = 1.4,{ }\eta = - 1,{ }\xi_{0} = - 1,{ }y = - \sqrt 2 ,{ }z = \sqrt 2 , $$

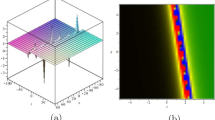
Figure 2 presents the graphical representation for different solutions of HNLS equation using F-expansion method.

Fig. 2

The solution structure for the obtained soliton solutions by F-expansion principle

In Fig. 2a, the dark-soliton solution ${\psi }_{5}$ is shown with

$$ B_{1} = { }B_{2} = 2,{ }B_{3} = - 2,{ }k_{1} = 1.1,{ }k_{2} = 9,{ }k_{3} = 2.3,{ }w = - 4.4,{ }y = 1,{ }z = 1, $$

While in Fig. 2b, the bright-soliton solution ${\psi }_{6}$ is illustrated with

$$ B_{1} = 1.1,{ }B_{2} = B_{3} = 1.2,{ }k_{1} = 0.5,{ }k_{2} = - 1,{ }k_{3} = { }w = 1,{ }y = - 2,{ }z = 2. $$

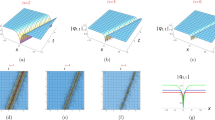
Figure 2c shows the singular soliton solution ${\psi }_{7}$ with

$$ B_{1} = - 2,{ }B_{2} = 1,{ }B_{3} = 2,{ }k_{1} = 0.5,{ }k_{2} = { }k_{3} = { }w = 1,{ }y = 3,{ }z = - 1.5. $$

In Fig. 2d, the singular-soliton solution ${\psi }_{8}$ is shown with

$$ B_{1} = 1,{ }B_{2} = B_{3} = 2,{ }k_{1} = k_{3} = 1,{ }k_{2} = - 0.7,{ }w = 1,{ }y = 2.2,{ }z = - 3. $$

Figure 2e–h shows the periodic singular soliton solutions ${\psi }_{9}, {\psi }_{10}, {\psi }_{11}$ and${\psi }_{12}$, respectively. The parameters values are ${B}_{1}={B}_{2}={B}_{3}={K}_{3}=w=y=z=1$ in such figures except for ${k}_{1}$ and${k}_{2}$, such that in Fig. (2-e), ${k}_{1}=0.5, {k}_{2}=-1,$ while in Fig. 2f, ${k}_{1}=1, {k}_{2}=-0.7$ but in Fig. 2g and h), ${k}_{1}=0.5 , {k}_{2}=1.$

Figure 2i and j shows the cluster-singular soliton solution ${\psi }_{13}$ and the dark-bright soliton solution ${\psi }_{14}$ with parameters values ${B}_{1}={B}_{2}={B}_{3}={k}_{2}={k}_{3}=w=y=z=1$ and ${k}_{1}=0.5$, while in Fig. 2k and l, the Cluster-singular periodic soliton solutions ${\psi }_{15}$ and ${\psi }_{16}$ are shown with ${B}_{1}={B}_{2}={B}_{3}={k}_{1}={k}_{3}=w=y=z=1, {k}_{2}=-0.7$ and ${B}_{1}=0.2, {B}_{2}={B}_{3}=0.5, {k}_{1}={k}_{3}=w=y=z=1, {k}_{2}=-0.5$, respectively.

5 Conclusion

In the present article, we have investigated the travelling wave solutions of the (3 + 1)-dimensional hyperbolic nonlinear Schrödinger equation (HNLS) because of its paramount importance in several applications such that it is used as a model for different physical phenomena such as the propagation of electromagnetic fields, the dynamics of optical soliton promulgation and the evolution of the water wave surface. The study was done from the point of view of two powerful methods, namely, Riccati equation technique and F-expansion principle. Different and new solutions were obtained for that equation and physically examined by graphical representations in 3d plots.