1 Introduction

The complicated dynamical communication of real-world phenomena can be demonstrated in knowing how to deviate an occurrence in terms of space and time. The partial differential equation has the most distinguished legacy for displaying how a physical phenomena is happening in space and time. Any physical phenomenon involving partial differential equations must be approached with the fundamental concept of the instantaneous rate of change. The classical theory of differentiation is the magnificent concept in the modern fields to explain the complicated natural phenomenons in a consistent fashion. However, the fractional differential theory is employed to discover the physical properties of several significant natural systems and to improve the effectiveness of already-existing inaccessible processes. The fractional differential theory is an extension of the basic differentiation theory, where the classical theory of differentiation has a week singularity, the theory of fractional differentiation is conceivable.

The various production of fractional differential operators is novel. A few significant and highly practical fractional operators are shown here like, Riemann-Liouville derivative and modified version (Guy 2006), Caputo operator (Michele 1967), conformable differential operator (Roshdi et al. 2014), truncated-M derivative (Sousa and Oliveira 2017), \(\beta\) differential operator (Alwyn 2006), Caputo-Fabrizio derivative with non-singular kernel (Michele and Fabrizio 2015) and also Attangana-Baleanu in Caputo and R-L sense encompassing non-singular kernel (Atangana and Baleanu 2016). The fractional partial differential equations permit us to generalize the classic partial differential equations and also allows one to uncover the chemistry of physical events in a cavernously and far-reaching sense. The analytical findings of the alcohol concentration in the blood and the alcohol concentration in the stomach are assessed using the Sumudu transform method by Singh Jagdev (2020). The Banach fixed point theorem approach is used to establish the existence and uniqueness of the solution of the fractional Coronavirus model, which is formulated in the Atangana-Baleanu-Caputo derivative sense (Ebenezer et al. 2021). Jagdev et al. (2022) analyzed and developed the fractional soliton solutions of the fractional Caudrey-Dodd-Gibbon equation. Behzad et al. (2022) studied the local fractional longitudinal wave equation in a magneto-electro-elastic circular rod in fractal media.

The partial differential equation carries at least one dependent variable which usually interprets any physical entity such as the surface height of water waves or magnitude of electromagnetic waves in connection to time. An extensive range of scientific areas utilise non-linear partial differential equations to incorporate non-linearity to the partial differential equation (Agrawal 2013; Muhammad et al. 2017; Kimeu 2009; Abdeljawad 2015; Roger et al. 1988). The partial differential equations encompassing non-linearity have quite an influence in diverse areas of mathematical sciences, engineering fields, and applied sciences. The study and analysis of non-linear partial differential equations through solitonic wave solutions is certainly a magnificent objective for scientific interpretation. On the account of obtaining the exact wave solutions and for reporting the intricated non-linear systems in the non-linear sciences, non-linear partial differential equations through solitonic wave solutions are a splendiferous and elevated avenue for physicists and mathematicians. The analysis of the serpentine physical process on the account of solitons is a spectacular study. The non-linear Schrödinger equation has been anatomized through a solitonic perspective in outrageous aspects (Xue et al. 2019; Weitian et al. 2019; Xiaoyan et al. 2019; Helal and Seadawy 2009; Seadawy 2015).

In certain scenarios, the combination of two fluids forms an instability which is classed as Kelvin Helmholtz instability (KHI). The instabilities of such type have consequential contributions in astrophysics, physics of space, fluids flow, and plasma physics. Few examples of this can see seen in the dynamical process of the radioactive galaxies in the jet zone, the spiral galaxy hose (Blandford et al. 1982), the planetary stratiform atmosphere, the dynamical procedure of the magnetic rupture zone at the boundary (Parhi 1992), the common tail (Schilinski and Chernii 1987), the stability of the plasma cutting flow connecting the solar wind to the magnetosphere (Min et al. 1997), the interface among conterminous flows of heterogeneous speed in solar wind (Parker 1963). The inquisition of the non-linear saturation phase of the cross-field electrostatic (KHI) in plasma sturdily magnetized is being impelled by the experiments in the laboratory (Khater et al. 2001, 2006; Nielsen et al. 1992). The instability of in-homogeneous plasma flux in cross the electric and magnetic fields is a remarkable certain process (Wang et al. 1992). The geomagnetic space of earth has distinct waves in the upper ionosphere (Lindqvist et al. 1994) and the auroral area (Temerin et al. 1979). Wu and Wang analyzed the solitary wave structures and vindicated the practicability of prosecution of their waves consequences of the non-linear system in the upper ionosphere with the assistance of scientific Freja satellite (Holback et al. 1994; De-Jin et al. 1996). Micheal picked a stability in-viscid, in-compressible, and entirely conducting fluid with a parallel uniform motion to their interfaces and also have homologous magnetic fields along the direction of flow (Michael 1955). On the basis of the account of the structure of the linear theory, Michael anticipated that the influence of the magnetic field is stable on a structure. Batiha et al. (2022) developed the solutions of Sturm-Liouville and Langevin equations with fractional operator and proved the existence and uniqueness. Albadarneh et al. (2021) constructed the analytical solutions by utilizing the new proposed scheme poer series method. Shatnawi et al. (2021) investigated the strongly fractional-order nonlinear Benchmark oscillatory problems by using the optimal homotopy asymptotic scheme.

Chandrashekhar has introduced the linear theory for the hegemonize Kelvin-Helmholtz instability in the magnetohydrodynamics of two moving fluids with uniform velocity (Chandrasekhar 1961). Nayfeh inspected the non-linear characteristics of Kelvin-Helmholtz instability concerning an ideal fluid (Hasan and Saric 1971). Kant examined the magnetohydrodynamics with stable wave packets nonlinear progression for the Kelvin-Helmholtz instability (Kant and Malik 1982). Kant proclaimed that the sub-critical magnetohydrodynamics flow with dissimilitude velocity is less than critical velocity. He also investigated that the dynamical model of amplitude generations is fundamentally non-linear Schrödinger equation. Kant also disclosed another point, namely that under the impact of the magnetic field, the magnetic amplitude of waves is unstable for modulation (Kant and Malik 1982). The inverse scattering transformation has been exploited to explore the solution of one-dimensional non-linear Schrödinger and analyzed that the solitary wave solution is expedited by smooth initial information and is also analogous to the final stage of modulation instability (Aleksei and Zakharov 1972).

The analysis of the 4th-order non-linear Schrödinger equation in sort of solitons with Ricatti-Bernoulli sub-ODE and \(tanh-coth\) expansion method is depicted in Mohamed et al. (2017). Inc investigates the solitonic structures of higher-order dispersive cubic quintic Schrödinger equations Inc et al. (2017). The modified Tanh-Coth scheme and the Riccati-Bernoulli sub-ordinary differential equation have been used to study the solitons of the non-linear evolution equation Inc et al. (2017). Solitary waves of the nonlinear Schrödinger equation have been studied using the fractional operator (Mustafa et al. 2018). The exact solutions of 2 distinct fifth-order non-linear partial differential equations have been examined using the Riccati-Bernoulli sub-ODE approach (Inc et al. 2017). The dynamic behavior of the ill-posed Boussinesq equation in shallow water and non-linear lattices has explained by Inc Fairouz et al. (2017). In order to study the category of long-wave unstable lubrication models, the Lie theory has been used Adil et al. (2020). Wave propagation in micro-structured solids with conformable time-fractional operators has been illustrated in this study Nauman et al. (2020). The exact Hirota-Maccari travelling wave solutions in the non-linear optics for the \((2+1)\)-dimensional system (Nauman et al. 2019). The analysis report of the generalised second-order nonlinear Schrödinger equation has been created by Raza Nauman et al. (2020). Asjad investigated 2D-chiral non-linear Schrödinger equation by executing two different techniques Hamood et al. (2021). It has become possible to derive the precise travelling wave solutions to the Schrödinger hyperbolic equation in Hamood-Ur et al. (2020).

The non-linear Schrödinger equations are primitive originators cataloging the physics of optical pulses of light in Kerr non-linearity media. An extensive class of striking and systematized techniques has been reconnoitering canonical and reliable solutions. Some of them are, symmetry strategy George and Kumei (2013), \(tanh-coth\) trigonometric function scheme Engui (2000), exp-function technique (Mingliang and Li 2005), Lie and Bäcklund transformation toll (Hai-Ping and Pan 2014) and extended trial equation technique (Nawaz et al. 2017), etc. This article aspires to comparatively analyze extricated traveling wave exact structures of elliptic non-linear schrödinger equation in the perspective of three distinct fractional derivatives and executing new direct extended algebraic strategy. The leading considered model is Seadawy et al. (2020),

$$\begin{aligned} 2i\Psi _{t}+\Psi _{xx}+\Psi _{yy}=\varrho |\Psi ^{2}|\Psi . \end{aligned}$$
(1)

This model is describing the phenomenon of the two fluids that were superimposed were separated by the interface at z = 0. The fluids are inviscid, in-compressible, semi-infinite, and conduct perfectly with surface tension at the boundary. The \((2+1)-\)dimensional dynamical nonlinear elliptic Schrödinger equation provides an illustration of the pulse propagation ahead of ultra-short range in optical communication systems. This model includes optical fibre and optical communication systems as its primary applications.

The current research article is planned as, Sect. 2 is committed for the preliminaries, in Sect. 3 fractional depiction of the governing model, Sect. 4 communicates the anatomization of technique, Sect. 5 reveals the solutions, and terminal Sect. 6 concludes the discussion.

2 Preliminaries

Here, we will dispute some germane notations and contributions which exploit to extract futuristic ideas.

2.1 Conformable fractional operator

Definition 1

Assume that a \(h: R^{+}\rightarrow R\) is differential function. The conformable derivative with fractional order \(0<\varpi \le 1\) as Abdeljawad (2015),

$$\begin{aligned} D^{\varpi }_{t}(h(t))=\lim _{\varepsilon \rightarrow 0}\frac{h(t+\varepsilon t^{1-\varpi })-h(t)}{\varepsilon }, \end{aligned}$$
(2)

where time is positive.

The fractional derivative’s features (Michael 1955).

\(\mathbf{{(1)}}:~D^{\varpi }_{t}t^{\varsigma }=\varsigma t^{\varsigma -\varpi },~~\forall \varsigma \in R.\)

\(\mathbf{{(2)}}:~D^{\varpi }_{t}(k(h(t)))=kD^{\varpi }_{t}(h(t)).\)

\(\mathbf{{(3)}}:~D^{\varpi }_{t}(m(h(t))+n(g(t)))=mD^{\varpi }_{t}(h(t))+nD^{\varpi }_{t}(g(t))~~\forall m,n\in R.\)

\(\mathbf{{(4)}}:~D^{\varpi }_{t}(\frac{g(t)}{h(t)})=\frac{(h(t))~D^{\varpi }_{t}(g(t))-(g(t))~D^{\varpi }_{t}(h(t))}{(h(t))^{2}}.\)

\(\mathbf{{(5)}}:~D^{\varpi }_{t}(g(t)*h(t))=(g(t))~D^{\varpi }_{t}(h(t))*(h(t))~D^{\varpi }_{t}(g(t)).\)

\(\mathbf{{(6)}}:~D^{\varpi }_{t}h(t)=t^{1-\varpi }\frac{dh}{dt}.\)

\(\mathbf{{(7)}}:~D^{\varpi }_{t}x^{\varsigma }=\frac{\Gamma {(1+\varsigma )}}{\Gamma {(1+\varsigma -\varpi )}}x^{\varsigma -\varpi },~~\varsigma \ge 0.\)

\(\mathbf{{(8)}}:~D^{\varpi }_{t}(c)=0~~\forall ~ constants.\)

\(\mathbf{{(9)}}:~D^{\varpi }_{t}((h(x))\circ (g(t)))=t^{1-\varpi }g'(t)h'(g(t)).\)

2.2 \(\beta -\)fractional derivative

Definition 2

It is defined as Kimeu (2009):,

$$\begin{aligned} {}_{0}^{B}D^{\varpi }_{x}(h(x))=\lim _{\varepsilon \rightarrow 0}\frac{h(x+\varepsilon (x+\frac{1}{\Gamma (\varpi )}))-h(x)}{\varepsilon }, \end{aligned}$$
(3)

The fractional differential operator’s characteristics are Kimeu (2009).

Theorem 1

Assume \(0<\varpi <1,~m,n,c\in R\) and differentiable functions h(x), g(x) with positive time:

\(\mathbf{{(1)}}:~{}_{0}^{B}D^{\varpi }_{x}(c)= 0,~ \forall ~constants.\)

\(\mathbf{{(2)}}:~{}_{0}^{B}D^{\varpi }_{x}(\frac{g(x)}{h(x)})=\frac{(h(x))~{}_{0}^{B}D^{\varpi }_{x}(g(x))-(g(x))~{}_{0}^{B}D^{\varpi }_{x}(h(x))}{(h(x))^{2}}.\)

\(\mathbf{{(3)}}:~{}_{0}^{B}D^{\varpi }_{x}(g(x)*h(x))=(g(x))~{}_{0}^{B}D^{\varpi }_{x}(h(x))*(h(x))~{}_{0}^{B}D^{\varpi }_{x}(g(x)).\)

\(\mathbf{{(4)}}:~{}_{0}^{B}D^{\varpi }_{x}(m(h(x))+n(g(x)))=m~{}_{0}^{B}D^{\varpi }_{x}(h(x))+n~{}_{0}^{B}D^{\varpi }_{x}(g(x))\).

\(\mathbf{{(5)}}:~{}_{0}^{B}D^{\varpi }_{x}(k(h(x)))=k~{}_{0}^{B}D^{\varpi }_{x}(g(x))(h(x)).\)

2.3 Truncated M-fractional operator

Definition 3

Assume a \(h: R^{+}\rightarrow R\) is differential function, which is define with \(0<\varpi <1\) fractional order Abdeljawad (2015):

$$\begin{aligned} {}_{i}D^{\varpi ,\gamma }_{M}(h(t))=\lim _{\varepsilon \rightarrow 0}\frac{h(t+{}_{i}E_{\gamma }(\varepsilon t^{-\varpi }))-h(t)}{\varepsilon }, \end{aligned}$$
(4)

where Mittag-leffer function \({}_{i}E_{\gamma }\) with one parameter.

Definition 4

It is defined in Abdeljawad (2015):

$$\begin{aligned} {}_{i}E_{\gamma }(Z)=\sum _{j=0}^{i}\frac{Z^{j}}{\Gamma (j\gamma +1)}, \end{aligned}$$
(5)

where \(Z\in C\) and \(\gamma >0\).

Theorem 2

As \(0<\varpi \le 1,~m,n,c\in R\) and h(x), g(x) are differentiable at \(t>o\) so:

The qualities of a fractional operator include Kimeu (2009):

\(\mathbf{{(1)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(m(h(t))+n(g(t)))=m~{}_{i}D^{\varpi ,\gamma }_{M}(h(t))+n~{}_{i}D^{\varpi ,\gamma }_{M}(g(t)).\)

\(\mathbf{{(2)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(g(t)*h(t))=(g(t))~{}_{i}D^{\varpi ,\gamma }_{M}(h(t))*(h(t))~{}_{i}D^{\varpi ,\gamma }_{M}(g(t)).\)

\(\mathbf{{(3)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(c)= 0.\)

\(\mathbf{{(4)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(k(h(t)))=k~{}_{i}D^{\varpi ,\gamma }_{M}(h(t)).\)

\(\mathbf{{(5)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(t^{\vartheta })=T^{\vartheta -\varpi }, ~~ \vartheta \in R .\)

\(\mathbf{{(6)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(h(g))(t)=h'(g~{}_{i}D^{\varpi ,\gamma }_{M}(g)).\)

\(\mathbf{{(7)}}:~{}_{i}D^{\varpi ,\gamma }_{M}(\frac{g(t)}{h(t)})=\frac{(h(t))~{}_{i}D^{\varpi ,\gamma }_{M}(g(t))-(g(t))~{}_{i}D^{\varpi ,\gamma }_{M}(h(t))}{(h(t))^{2}}.\)

3 Fractional presentation

The fractional representation of the assumed nonlinear partial differential equation shepherd with three distinct fractional operators.

(1): The conformable fractional operator ia applying on Eq. (1),

$$\begin{aligned} 2iD^{\varpi }_{t}\Psi +\Psi _{xx}+\Psi _{yy}-\varrho |\Psi |^{2}\Psi =0, \end{aligned}$$
(6)

where \(D^{\varpi }_{t}\) is the conformable operator concerning to t.

(2): The \(\beta -\)operator is applying on Eq. (1),

$$\begin{aligned} 2i~{}_{0}^{B}D^{\varpi }_{t}\Psi +{}_{0}^{B}D^{2\varpi }_{xx}\Psi +{}_{0}^{B}D^{2\varpi }_{y}\Psi -\varrho |\Psi |^{2}\Psi =0, \end{aligned}$$
(7)

where \({}_{0}^{B}D^{\varpi }_{t},~ {}_{0}^{B}D^{\varpi }_{x}\) and \({}_{0}^{B}D^{\varpi }_{y}\) are \(\beta -\)operator with reference to t, x and y respectively.

(3): The truncated-M operator is applying on Eq. (1),

$$\begin{aligned} 2i~{}_{i}D^{2\varpi ,\gamma }_{M,t}\Psi +{}_{i}D^{2\varpi ,\gamma }_{M,x}\Psi +{}_{i}D^{2\varpi ,\gamma }_{M,y}\Psi -\varrho |\Psi |^{2}\Psi =0, \end{aligned}$$
(8)

where \({}_{i}D^{\varpi ,\gamma }_{M,t}, ~{}_{i}D^{\varpi ,\gamma }_{M,x}\) and \({}_{i}D^{\varpi ,\gamma }_{M,y}\) are the \(\beta\) operators in sense of t,  x and y respectively.

3.1 Operational transformations

Here are the re-portable transformations for the anticipated PDE to ODE conversion for the solution of Eqs. (6), (7) and (8).

Let us consider some fractional operator-related functional transformations:

$$\begin{aligned} \Psi =\Psi (x,y,t),~~where~~\Psi (x,y,t)=\Phi (\tau )e^{i\psi },~ \end{aligned}$$
(9)

where \(\Phi\) is real function and \(\tau ~and~\psi\) is traced as per concerned fractional operators.

(1):  We designate \(\tau\) and \(\psi\) for the conformable fractional operator such as:

$$\begin{aligned} \tau= & {} \kappa _{1}x+\kappa _{2}y+(\frac{\sigma }{\varpi })t^{\varpi }, \end{aligned}$$
(10)
$$\begin{aligned} \psi= & {} b_{1}x+b_{2}y+(\frac{\lambda }{\varpi })t^{\varpi }+\theta . \end{aligned}$$
(11)

(2):  We designate \(\tau\) and \(\psi\) for the \(\beta\) fractional operator such as:

$$\begin{aligned} \tau= & {} \frac{\kappa _{1}}{\varpi }\bigg (x+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi }+\frac{\kappa _{2}}{\varpi }\bigg (y+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi } +\frac{\sigma }{\varpi }\bigg (t+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi }, \end{aligned}$$
(12)
$$\begin{aligned} \psi= & {} \frac{b_{1}}{\varpi }\bigg (x+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi }+\frac{b_{2}}{\varpi }\bigg (y+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi } +\frac{\lambda }{\varpi }\bigg (t+\frac{1}{\Gamma (\varpi )}\bigg )^{\varpi }+\theta _{0}(\tau ). \end{aligned}$$
(13)

(3):  We designate \(\tau\) and \(\psi\) for the truncated M-fractional operator such as:

$$\begin{aligned} \tau= & {} \frac{\Gamma (\gamma +1)}{\varpi }(\kappa _{1}x^{\varpi }+\kappa _{2}y^{\varpi }+\sigma t^{\varpi }), \end{aligned}$$
(14)
$$\begin{aligned} \psi= & {} \frac{\Gamma (\gamma +1)}{\varpi }(b_{1}x^{\varpi }+b_{2}y^{\varpi }+\lambda t^{\varpi })+\theta _{0}(\tau ), \end{aligned}$$
(15)

where \(\Phi (\tau )\) is the real function, \(\psi\) interprets the phase factor, frequency is reported by \(\lambda\), \(b_{1}\) and \(b_{2}\) are wave number.

4 New extended direct algebraic method

The proposed scheme is following Ali et al. (2020).

Assume a general non-linear partial differential equation:

$$\begin{aligned} P(\Psi ,\Psi _{t},\Psi _{x},\Psi _{y},\Psi _{tt},\Psi _{xx},...) = 0. \end{aligned}$$
(16)

It has susceptibility to attain the form of non-linear ordinary differential equation on the execution of complex traveling wave transformation such as:

$$\begin{aligned} \Psi (x,y,t)=\Phi (\tau )e^{i\psi }, \end{aligned}$$
(17)

where \(\tau =\kappa _{1}t+\kappa _{2}x+\kappa _{3}y\) and \(\psi =\kappa _{4}t+\kappa _{5}x+\kappa _{6}y+\theta\), we get:

$$\begin{aligned} \digamma (\Phi ,\Phi ',\Phi '',...) = 0, \end{aligned}$$
(18)

here, the notation of differentiation depicted by the prime in Eq. (18).

Assume that solution of Eq. (18) is:

$$\begin{aligned} \digamma (\tau )=a_{0}+\sum _{i=-m}^{m} \bigg [a_{i}(P(\tau ))^{i}\bigg ], \end{aligned}$$
(19)

where,

$$\begin{aligned} P'(\tau )=\ln (\rho )\left( \mu _{2} +\nu _{2} P(\tau ) + \zeta _{2} P^{2} (\tau )\right) ,~~~ \rho \ne 0,1, \end{aligned}$$
(20)

where \(\zeta _{2}\), \(\mu _{2}\) and \(\nu _{2}\) are real constants.

The general solutions with respect to parameters \(\mu _{2}\), \(\nu _{2}\) and \(\zeta _{2}\) of Eq. (20) are:

(Case 1): When \(\nu _{2}^2 - 4\mu _{2} \zeta _{2} < 0\) and \(\zeta _{2} \ne 0,\)

$$\begin{aligned} P_{1}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{-\Theta }}{2\zeta _{2}}\tan _{\rho }\left( \frac{\sqrt{-\Theta }}{2}\tau \right) . \end{aligned}$$
(21)
$$\begin{aligned} P_{2}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}-\frac{\sqrt{-\Theta }}{2\zeta _{2}}\cot _{\rho }\left( \frac{\sqrt{-\Theta }}{2}\tau \right) . \end{aligned}$$
(22)
$$\begin{aligned} P_{3}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{-\Theta }}{2\zeta _{2}}\left( \tan _{\rho }\left( \sqrt{-\Theta }\tau \right) \pm \sqrt{mn}\sec _{\rho }\left( \sqrt{-\Theta }\tau \right) \right) . \end{aligned}$$
(23)
$$\begin{aligned} P_{4}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{-\Theta }}{2\zeta _{2}}\left( \cot _{\rho }\left( \sqrt{-\Theta }\tau \right) \pm \sqrt{mn}\csc _{\rho }\left( \sqrt{-\Theta }\tau \right) \right) . \end{aligned}$$
(24)
$$\begin{aligned} P_{5}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{-\Theta }}{4\zeta _{2}}\left( \tan _{\rho } \left( \frac{\sqrt{-\Theta }}{4}\tau \right) - \cot _{\rho }\left( \frac{\sqrt{-\Theta }}{4}\tau \right) \right) . \end{aligned}$$
(25)

(Case 2): When \(\nu _{2}^2 - 4\mu _{2} \zeta _{2} > 0\) and \(\zeta _{2} \ne 0,\)

$$\begin{aligned} P_{6}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}-\frac{\sqrt{\Theta }}{2\zeta _{2}}\tanh _{\rho }\left( \frac{\sqrt{\Theta }}{2}\tau \right) . \end{aligned}$$
(26)
$$\begin{aligned} P_{7}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}-\frac{\sqrt{\Theta }}{2\zeta _{2}}\coth _{\rho }\left( \frac{\sqrt{\Theta }}{2}\tau \right) . \end{aligned}$$
(27)
$$\begin{aligned} P_{8}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{\Theta }}{2\zeta _{2}}\left( -\tanh _{\rho }\left( \sqrt{\Theta }\tau \right) \pm i\sqrt{mn}\ sech_{\rho }\left( \sqrt{\Theta }\tau \right) \right) . \end{aligned}$$
(28)
$$\begin{aligned} P_{9}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}+\frac{\sqrt{\Theta }}{2\zeta _{2}}\left( -\coth _{\rho }\left( \sqrt{\Theta }\tau \right) \pm \sqrt{mn} \text {csch}_{\rho }\left( \sqrt{\Theta }\tau \right) \right) . \end{aligned}$$
(29)
$$\begin{aligned} P_{10}(\tau )= & {} -\frac{\nu _{2}}{2\zeta _{2}}-\frac{\sqrt{\Theta }}{4\zeta _{2}}\left( \ tanh_{\rho }\left( \frac{\sqrt{\Theta }}{4}\tau \right) +\ coth_{\rho }\left( \frac{\sqrt{\Theta }}{4}\tau \right) \right) . \end{aligned}$$
(30)

(Case 3): When \(\mu _{2}\zeta _{2} > 0\) and \(\nu _{2}=0,\)

$$\begin{aligned} P_{11}(\tau )= & {} \sqrt{\frac{\mu _{2}}{\zeta _{2}}}\ tan_{\rho }\left( \sqrt{\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(31)
$$\begin{aligned} P_{12}(\tau )= & {} -\sqrt{\frac{\mu _{2}}{\zeta _{2}}}\ cot_{\rho }\left( \sqrt{\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(32)
$$\begin{aligned} P_{13}(\tau )= & {} \sqrt{\frac{\mu _{2}}{\zeta _{2}}}\left( \tan _{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\sec _{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(33)
$$\begin{aligned} P_{14}(\tau )= & {} \sqrt{\frac{\mu _{2}}{\zeta _{2}}}\left( -\cot _{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\text {csc}_{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(34)
$$\begin{aligned} P_{15}(\tau )= & {} \frac{1}{2}\sqrt{\frac{\mu _{2}}{\zeta _{2}}}\left( \tan _{\rho }\left( \frac{\sqrt{\mu _{2}\zeta _{2}}}{2}\tau \right) -\cot _{\rho }\left( \frac{\sqrt{\mu _{2}\zeta _{2}}}{2}\tau \right) \right) . \end{aligned}$$
(35)

(Case 4): When \(\mu _{2} \zeta _{2} < 0\) and \(\nu _{2}=0,\)

$$\begin{aligned} P_{16}(\tau )= & {} - \sqrt{-\frac{\mu _{2}}{\zeta _{2}}}\tanh _{\rho } \left( \sqrt{-\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(36)
$$\begin{aligned} P_{17}(\tau )= & {} - \sqrt{-\frac{\mu _{2}}{\zeta _{2}}}\coth _{\rho } \left( \sqrt{-\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(37)
$$\begin{aligned} P_{18}(\tau )= & {} \sqrt{-\frac{\mu _{2}}{\zeta _{2}}}\left( -\tanh _{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \pm i \sqrt{mn}\text {sech}_{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(38)
$$\begin{aligned} P_{19}(\tau )= & {} \sqrt{-\frac{\mu _{2}}{\zeta _{2}}}\left( -\coth _{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\ csch_{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(39)
$$\begin{aligned} P_{20}(\tau )= & {} -\frac{1}{2} \sqrt{-\frac{\mu _{2}}{\zeta _{2}}} \left( \tanh _{\rho } \left( \frac{\sqrt{-\mu _{2}\zeta _{2}}}{2}\tau \right) +\ coth_{\rho } \left( \frac{\sqrt{-\mu _{2}\zeta _{2}}}{2}\tau \right) \right) . \end{aligned}$$
(40)

(Case 5): When \(\nu _{2} = 0\) and \(\mu _{2}=\zeta _{2},\)

$$\begin{aligned} P_{21}(\tau )= & {} \tan _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(41)
$$\begin{aligned} P_{22}(\tau )= & {} -\cot _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(42)
$$\begin{aligned} P_{23}(\tau )= & {} \tan _{\rho }\left( 2\mu _{2}\tau \right) \pm \sqrt{mn}\sec _{\rho }\left( 2\mu _{2}\tau \right) . \end{aligned}$$
(43)
$$\begin{aligned} P_{24}(\tau )= & {} -\cot _{\rho }\left( 2\mu _{2}\tau \right) \pm \sqrt{mn}\csc _{\rho }\left( 2\mu _{2}\tau \right) . \end{aligned}$$
(44)
$$\begin{aligned} P_{25}(\tau )= & {} \frac{1}{2}\left( \tan _{\rho }\left( \frac{\mu _{2}}{2}\tau \right) -\cot _{\rho }\left( \frac{\mu _{2}}{2}\tau \right) \right) . \end{aligned}$$
(45)

(Case 6): When \(\nu _{2} = 0\) and \(\zeta _{2}=-\mu _{2},\)

$$\begin{aligned} P_{26}(\tau )= & {} -\tanh _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(46)
$$\begin{aligned} P_{27}(\tau )= & {} -\coth _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(47)
$$\begin{aligned} P_{28}(\tau )= & {} -\tanh _{\rho }\left( 2\mu _{2}\tau \right) \pm i \sqrt{mn}\ sech_{\rho }\left( 2\mu _{2}\tau \right) . \end{aligned}$$
(48)
$$\begin{aligned} P_{29}(\tau )= & {} -\cot _{\rho }\left( 2\mu _{2}\tau \right) \pm \sqrt{mn}\ csch_{\rho }\left( 2\mu _{2}\tau \right) . \end{aligned}$$
(49)
$$\begin{aligned} P_{30}(\tau )= & {} -\frac{1}{2}\left( \tanh _{\rho }\left( \frac{ \mu _{2}}{2}\tau \right) +\cot _{\rho }\left( \frac{ \mu _{2}}{2}\tau \right) \right) . \end{aligned}$$
(50)

(Case 7): When \(\nu _{2}^2 = 4\mu _{2}\zeta _{2}\),

$$\begin{aligned} P_{31}(\tau )= \frac{-2\mu _{2}(\nu _{2}\tau \ln \rho +2) }{\nu _{2}^2 \tau \ln \rho }. \end{aligned}$$
(51)

(Case 8): When \(\nu _{2} = p,\mu _{2}= pq, (q\ne 0)\) and \(\zeta _{2}=0\),

$$\begin{aligned} P_{32}(\tau )=\rho ^{p\tau } -q. \end{aligned}$$
(52)

(Case 9): When \(\nu _{2} = \zeta _{2} = 0\),

$$\begin{aligned} P_{33}(\tau )=\mu _{2}\tau \ln \rho . \end{aligned}$$
(53)

(Case 10): When \(\nu _{2} = \mu _{2} = 0\),

$$\begin{aligned} P_{34}(\tau )=\frac{-1}{\zeta _{2} \tau \ln \rho }. \end{aligned}$$
(54)

(Case 11): When \(\mu _{2} = 0\) and \(\nu _{2} \ne 0\),

$$\begin{aligned} P_{35}(\tau )= & {} -\frac{m\nu _{2}}{\zeta _{2}\left( \cosh _{\rho }\left( \nu _{2}\tau \right) -\sinh _{\rho }\left( \nu _{2}\tau \right) + m \right) }. \end{aligned}$$
(55)
$$\begin{aligned} P_{36}(\tau )= & {} -\frac{\nu _{2}\left( \sinh _{\rho }\left( \nu _{2}\tau \right) +\cosh _{\rho }\left( \nu _{2}\tau \right) \right) }{\zeta _{2}\left( \sinh _{\rho }\left( \nu _{2}\tau \right) +\cosh _{\rho }\left( \nu _{2}\tau \right) + n \right) }. \end{aligned}$$
(56)

(Case 12): When \(\nu _{2} = p, \zeta _{2}=pq,~(q\ne 0\) and \(\mu _{2}=0)\),

$$\begin{aligned} P_{37}(\tau )= & {} -\frac{m\rho ^{p\tau }}{m-qn\rho ^{p\tau }}.\\ \sinh _{\rho }(\tau )= & {} \frac{m\rho ^\tau - n\rho ^{-\tau }}{2},~ \cosh _{\rho }(\tau )=\frac{m\rho ^\tau + n\rho ^{-\tau }}{2},\nonumber \\ \tanh _{\rho }(\tau )= & {} \frac{m\rho ^\tau - n\rho ^{-\tau }}{m\rho ^\tau + n\rho ^{-\tau }}, ~ \coth _{\rho }(\tau )=\frac{m\rho ^\tau + n\rho ^{-\tau }}{m\rho ^\tau - n\rho ^{-\tau }},\nonumber \\ \ sech_{\rho }(\tau )= & {} \frac{2}{m\rho ^\tau + n\rho ^{-\tau }},~\ csch_{\rho }(\tau )=\frac{2}{m\rho ^\tau - n\rho ^{-\tau }},\nonumber \\ \ sin_{\rho }(\tau )= & {} \frac{m\rho ^{i\tau } - n\rho ^{-i\tau }}{2i},~ \ coP_{\rho }(\tau )=\frac{m\rho ^{i\tau } + n\rho ^{-i\tau }}{2},\nonumber \\ \tan _{\rho }(\tau )= & {} -i\frac{m\rho ^{i\tau } - n\rho ^{-i\tau }}{m\rho ^{i\tau } + n\rho ^{-i\tau }}, ~~ \cot _{\rho }(\tau )=i\frac{m\rho ^{i\tau } + n\rho ^{-i\tau }}{m\rho ^{i\tau } - n\rho ^{-i\tau }},\nonumber \\ \sec _{\rho }(\tau )= & {} \frac{2}{m\rho ^\tau + n\rho ^{-\tau }},~~ \csc _{\rho }(\tau )=\frac{2i}{m\rho ^\tau - n\rho ^{-\tau }},\nonumber \end{aligned}$$
(57)

The deformation parameters m and n are arbitrary constants greater than zero.

4.1 Application to Eq. (16)

Operating the Eq. (9) to the Eqs. (6), (7) and (8) and equating real and imaginary part respectively:

$$\begin{aligned} (\kappa ^{2}_{1}+ & {} \kappa ^{2}_{2})\Phi ''-(b^{2}_{1}+b^{2}_{2}+2\lambda )\Phi -\varrho \Phi ^{3}=0. \end{aligned}$$
(58)
$$\begin{aligned} \sigma= & {} -\kappa _{1}b_{1}-\kappa _{2}b_{2}. \end{aligned}$$
(59)

Plugging the homogeneous balancing constant in Eq. (19), thus the solution is:

$$\begin{aligned} \Phi (\tau )=a_{0}+ a_{1}(P(\tau )), \end{aligned}$$
(60)

where,

$$\begin{aligned} P'(\tau )=\ln (\rho )\left( \mu _{2} +\nu _{2} P(\tau ) + \zeta _{2} P^2 (\tau )\right) ,~~~ \rho \ne 0,1. \end{aligned}$$
(61)

The predicted solution Eq. (60) subsituting in Eq. (58) and separating the coefficient of different powers of \((\tau )\), thus we have an algebraic system of equations.

The acquired algebraic system solve with the assistance of Mathematica and obtain:

$$\begin{aligned}&\left[ a_{0}=\pm \frac{\nu _{2}\sqrt{\kappa ^{2}_{1}+\kappa ^{2}_{2}}\log [\rho ]}{\sqrt{2\varrho }},~ a_{1}=\pm \frac{2\zeta _{2}\sqrt{\kappa ^{2}_{1}+\kappa ^{2}_{2}}\log [\rho ]}{\sqrt{2\varrho }},\right. \nonumber \\&\left. \lambda =-\frac{b^{2}_{1}+b^{2}_{2}}{2}-\frac{(\kappa ^{2}_{1}+\kappa ^{2}_{2})\Theta \log [\rho ]^{2}}{4},\right] \end{aligned}$$
(62)

where,

$$\begin{aligned} \Theta =\nu _{2}^{2}-4\mu _{2}\zeta _{2}. \end{aligned}$$

The general solution of Eq. (1) by plugging Eq. (62) in Eq. (19) is:

$$\begin{aligned} \Psi (x,y,t)=\pm \frac{\nu _{2}\sqrt{\kappa ^{2}_{1}+\kappa ^{2}_{2}}\log [\rho ]}{\sqrt{2\varrho }} \pm \frac{2\zeta _{2}\sqrt{\kappa ^{2}_{1}+\kappa ^{2}_{2}}\log [\rho ]}{\sqrt{2\varrho }}\left( P_{i}(\tau )\right) . \end{aligned}$$
(63)

5 Traveling wave solution

Now, we will acquire distinct solutions by choosing \(P_{i}\) from (21)–(57) respectively.

(Case 1): When \(\nu _{2}^2 - 4\mu _{2} \zeta _{2} < 0\) and \(\zeta _{2} \ne 0,\)

$$\begin{aligned} \Psi _{1}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\tan _{\rho }\left( \frac{\sqrt{-\Theta }}{2}\tau \right) . \end{aligned}$$
(64)
$$\begin{aligned} \Psi _{2}(x,y,t)= & {} \mp \Upsilon \sqrt{-\Theta }\cot _{\rho }\left( \frac{\sqrt{-\Theta }}{2}\tau \right) . \end{aligned}$$
(65)
$$\begin{aligned} \Psi _{3}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\left( \tan _{\rho }\left( \sqrt{-\Theta }\tau \right) \pm \sqrt{mn}\sec _{\rho }\left( \sqrt{-\Theta }\tau \right) \right) . \end{aligned}$$
(66)
$$\begin{aligned} \Psi _{4}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\left( \cot _{\rho }\left( \sqrt{-\Theta }\tau \right) \pm \sqrt{mn}\csc _{\rho }\left( \sqrt{-\Theta }\tau \right) \right) . \end{aligned}$$
(67)
$$\begin{aligned} \Psi _{5}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\left( \tan _{\rho } \left( \frac{\sqrt{-\Theta }}{4}\tau \right) - \cot _{\rho }\left( \frac{\sqrt{-\Theta }}{4}\tau \right) \right) . \end{aligned}$$
(68)

(Case 2): When \(\nu _{2}^2 - 4\mu _{2} \zeta _{2} > 0\) and \(\zeta _{2} \ne 0,\)

$$\begin{aligned} \Psi _{6}(x,y,t)= & {} \mp \Upsilon \sqrt{-\Theta }\tanh _{\rho }\left( \frac{\sqrt{\Theta }}{2}\tau \right) . \end{aligned}$$
(69)
$$\begin{aligned} \Psi _{7}(\tau )= & {} \mp \Upsilon \sqrt{-\Theta }\coth _{\rho }\left( \frac{\sqrt{\Theta }}{2}\tau \right) . \end{aligned}$$
(70)
$$\begin{aligned} \Psi _{8}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\left( -\tanh _{\rho }\left( \sqrt{\Theta }\tau \right) \pm i\sqrt{mn}\text {sech}_{\rho }\left( \sqrt{\Theta }\tau \right) \right) . \end{aligned}$$
(71)
$$\begin{aligned} \Psi _{9}(x,y,t)= & {} \pm \Upsilon \sqrt{-\Theta }\left( -\coth _{\rho }\left( \sqrt{\Theta }\tau \right) \pm \sqrt{mn} \text {csch}_{\rho }\left( \sqrt{\Theta }\tau \right) \right) . \end{aligned}$$
(72)
$$\begin{aligned} \Psi _{10}(x,y,t)= & {} \mp \Upsilon \sqrt{-\Theta }{4\zeta _{2}}\left( \ tanh_{\rho }\left( \frac{\sqrt{\Theta }}{4}\tau \right) +\ coth_{\rho }\left( \frac{\sqrt{\Theta }}{4}\tau \right) \right) . \end{aligned}$$
(73)

(Case 3): When \(\mu _{2}\zeta _{2} > 0\) and \(\nu _{2}=0,\)

$$\begin{aligned} \Psi _{11}(x,y,t)= & {} \pm 2\Upsilon \left( \sqrt{\zeta _{2}\mu _{2}}\ tan_{\rho }\left( \sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(74)
$$\begin{aligned} \Psi _{12}(x,y,t)= & {} \mp 2\Upsilon \left( \sqrt{\zeta _{2}\mu _{2}}\ cot_{\rho }\left( \sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(75)
$$\begin{aligned} \Psi _{13}(x,y,t)= & {} \pm 2\Upsilon \sqrt{\zeta _{2}\mu _{2}}\left( \tan _{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\text {sec}_{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(76)
$$\begin{aligned} \Psi _{14}(x,y,t)= & {} \pm 2\Upsilon \sqrt{\zeta _{2}\mu _{2}}\left( -\cot _{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\text {csc}_{\rho }\left( 2\sqrt{\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(77)
$$\begin{aligned} \Psi _{15}(x,y,t)= & {} \pm \Upsilon \sqrt{\zeta _{2}\mu _{2}}\left( \tan _{\rho }\left( \frac{\sqrt{\mu _{2}\zeta _{2}}}{2} \tau \right) -\cot _{\rho }\left( \frac{\sqrt{\mu _{2}\zeta _{2}}}{2}\tau \right) \right) . \end{aligned}$$
(78)

(Case 4): When \(\mu _{2} \zeta _{2} < 0\) and \(\nu _{2}=0,\)

$$\begin{aligned} \Psi _{16}(x,y,t)= & {} \mp 2\Upsilon \sqrt{-\mu _{2}\zeta _{2}}\tanh _{\rho } \left( \sqrt{-\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(79)
$$\begin{aligned} \Psi _{17}(x,y,t)= & {} \mp 2\Upsilon \sqrt{-\mu _{2}\zeta _{2}}\coth _{\rho } \left( \sqrt{-\mu _{2}\zeta _{2}}\tau \right) . \end{aligned}$$
(80)
$$\begin{aligned} \Psi _{18}(x,y,t)= & {} \pm 2\Upsilon \sqrt{-\mu _{2}\zeta _{2}}\left( -\tanh _{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \pm i \sqrt{mn}\text {sech}_{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(81)
$$\begin{aligned} \Psi _{19}(x,y,t)= & {} \pm 2\Upsilon \sqrt{-\mu _{2}\zeta _{2}}\left( -\coth _{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \pm \sqrt{mn}\ csch_{\rho }\left( 2\sqrt{-\mu _{2}\zeta _{2}}\tau \right) \right) . \end{aligned}$$
(82)
$$\begin{aligned} \Psi _{20}(x,y,t)= & {} \mp \Upsilon \sqrt{-\mu _{2} \zeta _{2}} \left( \tanh _{\rho } \left( \frac{\sqrt{-\mu _{2}\zeta _{2}}}{2}\tau \right) +\ coth_{\rho } \left( \frac{\sqrt{-\mu _{2}\zeta _{2}}}{2}\tau \right) \right) . \end{aligned}$$
(83)

(Case 5): When \(\nu _{2} = 0\) and \(\mu _{2}=\zeta _{2},\)

$$\begin{aligned} \Psi _{21}(x,y,t)= & {} \pm 2\zeta _{2}\Upsilon \left( \tan _{\rho }\left( \zeta _{2}\tau \right) \right) . \end{aligned}$$
(84)
$$\begin{aligned} \Psi _{22}(x,y,t)= & {} \mp 2\zeta _{2}\Upsilon \left( \cot _{\rho }\left( \zeta _{2}\tau \right) \right) . \end{aligned}$$
(85)
$$\begin{aligned} \Psi _{23}(x,y,t)= & {} \pm 2\zeta _{2}\Upsilon \left( \tan _{\rho }\left( 2\zeta _{2}\tau \right) \pm \sqrt{mn}\sec _{\rho }\left( 2\zeta _{2}\tau \right) \right) . \end{aligned}$$
(86)
$$\begin{aligned} \Psi _{24}(x,y,t)= & {} \pm 2\zeta _{2}\Upsilon \left( -\cot _{\rho }\left( 2\zeta _{2}\tau \right) \pm \sqrt{mn}\csc _{\rho }\left( 2\zeta _{2}\tau \right) \right) . \end{aligned}$$
(87)
$$\begin{aligned} \Psi _{25}(x,y,t)= & {} \pm \zeta _{2}\Upsilon \left( \tan _{\rho }\left( \frac{\zeta _{2}}{2}\tau \right) -\cot _{\rho }\left( \frac{\zeta _{2}}{2}\tau \right) \right) . \end{aligned}$$
(88)

(Case 6): When \(\nu _{2} = 0\) and \(\zeta _{2}=-\mu _{2},\)

$$\begin{aligned} \Psi _{26}(x,y,t)= & {} \pm 2\mu _{2}\Upsilon \tanh _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(89)
$$\begin{aligned} \Psi _{27}(x,y,t)= & {} \pm 2\mu _{2}\Upsilon \coth _{\rho }\left( \mu _{2}\tau \right) . \end{aligned}$$
(90)
$$\begin{aligned} \Psi _{28}(x,y,t)= & {} \mp 2\mu _{2}\Upsilon \left( -\tanh _{\rho }\left( 2\mu _{2}\tau \right) \pm i \sqrt{mn}\ sech_{\rho }\left( 2\mu _{2}\tau \right) \right) . \end{aligned}$$
(91)
$$\begin{aligned} \Psi _{29}(x,y,t)= & {} \mp 2\mu _{2}\Upsilon \left( -\cot _{\rho }\left( 2\mu _{2}\tau \right) \pm \sqrt{mn}\ csch_{\rho }\left( 2\mu _{2}\tau \right) \right) . \end{aligned}$$
(92)
$$\begin{aligned} \Psi _{30}(x,y,t)= & {} \pm \mu _{2}\Upsilon \left( \tanh _{\rho }\left( \frac{ \mu _{2}}{2}\tau \right) +\cot _{\rho }\left( \frac{ \mu _{2}}{2}\tau \right) \right) . \end{aligned}$$
(93)

(Case 7): When \(\nu _{2}^2 = 4\mu _{2}\zeta _{2}\),

$$\begin{aligned} \Psi _{31}(x,y,t)= \pm \nu _{2}\Upsilon \mp 4\zeta _{2}\Upsilon \left( \frac{\mu _{2}(\nu _{2}\tau \ln \rho +2) }{\nu _{2}^2 \tau \ln \rho }\right) . \end{aligned}$$
(94)

(Case 8): When \(\nu _{2} = p,\mu _{2}= pq, (q\ne 0)\) and \(\zeta _{2}=0\),

$$\begin{aligned} \Psi _{32}(x,y,t)=trivial. \end{aligned}$$
(95)

(Case 9): When \(\nu _{2} = \zeta _{2} = 0\),

$$\begin{aligned} \Psi _{33}(x,y,t)=0. \end{aligned}$$
(96)

(Case 10): When \(\nu _{2} = \mu _{2} = 0\),

$$\begin{aligned} \Psi _{34}(x,y,t)=\mp 2\Upsilon \left( \frac{1}{\tau \ln \rho }\right) . \end{aligned}$$
(97)

(Case 11): When \(\mu _{2} = 0\) and \(\nu _{2} \ne 0\),

$$\begin{aligned} \Psi _{35}(x,y,t)= & {} \pm \nu _{2}\Upsilon \mp 2\Upsilon \left( \frac{m\nu _{2}}{\left( \cosh _{\rho }\left( \nu _{2}\tau \right) -\sinh _{\rho }\left( \nu _{2}\tau \right) + m \right) }\right) . \end{aligned}$$
(98)
$$\begin{aligned} \Psi _{36}(x,y,t)= & {} \pm \nu _{2}\Upsilon \mp 2\Upsilon \left( \frac{\nu _{2}\left( \sinh _{\rho }\left( \nu _{2}\tau \right) +\cosh _{\rho }\left( \nu _{2}\tau \right) \right) }{\left( \sinh _{\rho }\left( \nu _{2}\tau \right) +\cosh _{\rho }\left( \nu _{2}\tau \right) + n \right) }\right) . \end{aligned}$$
(99)

(Case 12): When \(\nu _{2} = p, \zeta _{2}=pq,~(q\ne 0\) and \(\mu _{2}=0)\),

$$\begin{aligned} \Psi _{37}(x,y,t) =\pm p\Upsilon \mp 2 pq\Upsilon \left( \frac{m\rho ^{p\tau }}{m-qn\rho ^{p\tau }}\right) , \end{aligned}$$
(100)

where,

$$\begin{aligned} \Upsilon =\pm \frac{\sqrt{\kappa ^{2}_{1}+\kappa ^{2}_{2}}\log [\rho ]}{\sqrt{2\varrho }}. \end{aligned}$$

The parameters \(\tau\) and \(\psi\) are set out as Eqs. (10, 11), Eqs. (12, 13) and Eqs. (14, 15) associated with conformable operator, \(\beta\)-operator and truncated M-fractional operator respectively.

Fig. 1
figure 1

3D portraying for \(\Psi _{21}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 2
figure 2

2D and 3D portraying for \(\Psi _{21}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 3
figure 3

2D portraying for \(\Psi _{21}\) with the disparity of fractional operators and fractional order and also comparision at classic order

Full size image
Fig. 4
figure 4

3D portraying for \(\Psi _{36}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 5
figure 5

2D and 3D portraying for \(\Psi _{36}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 6
figure 6

2D portraying for \(\Psi _{36}\) with the disparity of fractional operators and fractional order and also comparision at classic order

Full size image
Fig. 7
figure 7

3D portraying for \(\Psi _{37}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 8
figure 8

2D and 3D portraying for \(\Psi _{37}\) with the disparity of fractional operators and fractional order

Full size image
Fig. 9
figure 9

2D portraying for \(\Psi _{37}\) with the disparity of fractional operators and fractional order and also comparision at classic order

Full size image

6 Graphically review

The fractional order of the operators is belonging to (0,1). There are infinite non-integer values in (0,1), so one can choose the value fractional order according to physical phenomenon. In this study we need to investigate the model and compare the results, thus choose the different values of fractional order from interval with sub-diffusivity.

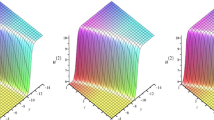
Figure 1: Depicts the 3D graphic comparison of dissimilar fractional differential operators for \(\Psi _{21}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\zeta _{2}=1\) and \(\varrho =1\).

Figure 1a–c yields 3D illustration at \(\varpi =0.1\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

Figure 1d–f yields 3D illustration at \(\varpi =0.5\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of analysis, the \(\beta\) and truncated M-fractional definitions rendering almost symmetrical curve with little bit difference, however, conformable fractional derivative interprets a prominent variance rather than \(\beta\) and truncated M-fractional operator.

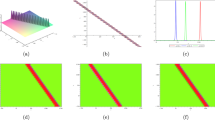
Figure 2: Chronicle the 3D and 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{21}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\zeta _{2}=1~and~\varrho =1\).

Figure 2a–c yields 3D illustration at \(\varpi =0.9\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of 3D analysis, the \(\beta\) and truncated M-fractional definitions rendering almost symmetrical curve with little bit difference, however, conformable fractional derivative interprets a prominent variance rather than \(\beta\) and truncated M-fractional operator.

Figure 2d capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 2e remit 2D comparision of executed fractional definitions at \(\varpi =0.3\), and Fig. 2f permit 2D comparision of exploited fractional definitions at \(\varpi =0.5\).

On the whole 2D inspection, the \(\beta\) and truncated M-fractional definitions manifesting almost the same pattern with little bit difference, however, conformable fractional derivative interprets a prominent variance rather than \(\beta\) and truncated M-fractional operator.

Figure 3 Represent the 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{21}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\zeta _{2}=1~and~\varrho =1\).

Figure 3a capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 3b remit 2D comparision of executed fractional definitions at \(\varpi =0.3\) and display the same locus as described above for 2D in Fig. 2.

Figure 3c contribute 2D comparision for conformable operator by varying fractional order, Fig. 3d contribute 2D comparision for \(\beta\) operator by varying fractional order, and Fig. 3e contribute 2D comparision for truncated M-fractional operator by varying fractional order.

Figure 3f delineates the comparison of prosecuted operators at classical order of derivative, which presents the efficiency of operators.

Entirely, when we analyzed all fractional 2D presentations against a single solution from the perspective of classical 2D presentation, thus we concluded that fractional study interprets deep knowledge of natural phenomenon rather than classical theory.

Remark

The solution \(\Psi _{21}\) is displaying the periodic-singular and dark-periodic- singular soliton solution as the fractional order increasing towards classical order.

Figure 4: Depicts the 3D graphic comparison of dissimilar fractional differential operators for \(\Psi _{36}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\nu _{2}=1~and~\varrho =1\).

Figure 4a–c yields 3D illustration at \(\varpi =0.1\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

Figure 4d–f yields 3D illustration at \(\varpi =0.5\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of analysis, the conformable and truncated M-fractional definitions rendering almost symmetrical curve with little bit difference, however, \(\beta\) fractional derivative interprets a prominent variance rather than \(\beta\) and truncated M-fractional operator.

Figure 5: Chronicle the 3D and 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{36}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\nu _{2}=1~and~\varrho =1\).

Figure 5a–c yields 3D illustration at \(\varpi =0.9\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of 3D analysis, as we move towards integer order then conformable and truncated M-fractional definitions rendering almost symmetrical curve with little bit difference, however, \(\beta\) fractional derivative interprets a prominent variance rather than conformable and truncated M-fractional operator.

Figure 5d capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 5e remit 2D comparision of executed fractional definitions at \(\varpi =0.3\), and Fig. 5f permit 2D comparision of exploited fractional definitions at \(\varpi =0.5\).

On the whole 2D inspection, the conformable and truncated M-fractional definitions manifesting almost the same pattern with little bit difference, however, \(\beta\) fractional derivative interprets a prominent variance rather than \(\beta\) and truncated M-fractional operator.

Figure 6: Represent the 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{36}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~\nu _{2}=1~and~\varrho =1\).

Figure 6a capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 6b remit 2D comparision of executed fractional definitions at \(\varpi =0.3\) and display the same locus as described above for 2D in Fig. 2.

Figure 6c contribute 2D comparision for conformable operator by varying fractional order, Fig. 6d contribute 2D comparision for \(\beta\) operator by varying fractional order, and Fig. 6e contribute 2D comparision for truncated M-fractional operator by varying fractional order.

Figure 6f delineates the comparison of prosecuted operators at classical order of derivative, which presents the efficiency of operators.

Entirely, when we analyzed all fractional 2D presentations against a single solution from the perspective of classical 2D presentation, thus we concluded that fractional study interprets deep knowledge of natural phenomenon rather than classical theory.

Remark

The solution \(\Psi _{36}\) is displaying the dark-singular and kink-periodic- singular soliton solution as the fractional order increasing towards classical order.The \(\beta\) fractional operator demonstrate the disparate behavior compare to conformable and truncated M-fractional derivative.

Figure 7: Depicts the 3D graphic comparison of dissimilar fractional differential operators for \(\Psi _{37}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~p=q=1~and~\varrho =1\).

Figure 7a–c yields 3D illustration at \(\varpi =0.1\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

Figure 7d–f yields 3D illustration at \(\varpi =0.5\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of analysis, the conformable , \(\beta\) and truncated M-fractional definitions rendering almost distinct pattern.

Figure 8: Chronicle the 3D and 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{37}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~p=q=1~and~\varrho =1\).

Figure 8a–c yields 3D illustration at \(\varpi =0.9\) concerning to conformable operator, \(\beta -\)fractional definition and truncated M-fractional derivative respectively.

On the account of 3D analysis, conformable , \(\beta\) and truncated M-fractional definitions rendering almost symmetrical curve with little bit difference.

Figure 8d capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 8e remit 2D comparision of executed fractional definitions at \(\varpi =0.3\), and Fig. 8f permit 2D comparision of exploited fractional definitions at \(\varpi =0.5\).

On the whole 2D inspection, the conformable , \(\beta\) and truncated M-fractional definitions manifesting almost the different pattern with little bit difference.

Figure 9: Represent the 2D graphic comparison of dissimilar fractional differential operators for \(\Psi _{37}\) at the variation of fractional order along with practicable parametric values such as, \(\rho =e,~\kappa _{1}=1,~\kappa _{2}=1,~b_{1}=1,~b_{2}=1,~p=q=1~and~\varrho =1\).

Figure 9a capitulate 2D comparision of utilized fractional definitions at \(\varpi =0.1\), Fig. 9b remit 2D comparision of executed fractional definitions at \(\varpi =0.3\) and display the same locus as described above for 2D in Fig. 2.

Figure 9c contribute 2D comparision for conformable operator by varying fractional order, Fig. 9d contribute 2D comparision for \(\beta\) operator by varying fractional order, and Fig. 9e contribute 2D comparision for truncated M-fractional operator by varying fractional order.

Figure 9f delineates the comparison of prosecuted operators at classical order of derivative, which presents the efficiency of operators.

Entirely, when we analyzed all fractional 2D presentations against a single solution from the perspective of classical 2D presentation, thus we concluded that fractional study interprets deep knowledge of natural phenomenon rather than classical theory.

Remark

The solution \(\Psi _{37}\) is displaying the singular and bright-singular with one kink soliton solution as the fractional order increasing towards classical order. As we move far away to integer-order then conformable , beta, and truncated M-fractional differential operators displayed distinct behavior, however, when we take stem towards classical order, thus they try to coincide.

7 Conclusion

The non-linear elliptic Schrödinger equation is constituted in the form of a fractional partial differential equation by using the conformable operator, \(\beta\) operator, and truncated M-fractional derivative.The next wave traveling wave transformations have been developed to transformed PDE into ODE corresponding to considered fractional operators. The new direct extended algebraic technique has been successfully practiced to obtain solitonic structures. As result, the fractional analytical solutions such as, plane solution, mixed hyperbolic solution, periodic and mixed periodic solutions, mixed trigonometric solution, trigonometric solution, shock solution, mixed shock singular solution, mixed singular solution, complex solitary shock solution, singular solution and shock wave solutions are obtained. The acquired analytical solitary wave solutions have key applications to the optical fibers and optical communication process. An enormous study for the propagation of the pulses onward to ultra-short range in the optical communications process has been demonstrated through the fractional dynamical equation. The graphical visualization has presented of the obtained three different solutions with the assistance of Mathematica. The comparision of the considered fractional operators is graphically presented. The impact of fractional order is also displayed and concluded that the fractional order is responsible to control the singularity of the solutions. The effectiveness and simplicity of the utilized technique are realized from computed results. Therefore, it can be applied to other generated models in engineering and mathematics. The researchers can be explored this study furthermore in the sense of bifurcation analysis and Chaos analysis to study the phase portraits and chaotic behaviour of the model. The modulational instability gain spectrum can be developed and the sensitivity of equation can be verified by apply the sensitive analysis.