1 Introduction

Controlling the phase of an optical signal is an essential process in any optical signal processing operation. In interferometric optical systems as well as beam forming systems, this allows controlling the spatial distribution of the optical beam. Recently, there has been an increased interest in such optical phase shifters for building optical mode converters as well as mode multiplexers that are required for optical communication systems to increase system capacity through mode division multiplexing (MDM) (Leuthol et al. 1998; El-Sabban and Khalil 2016; Mehrabi and Zarifkar 2019; Shalaby 2018; Berdagué and Facq 1982).

In mode converter applications, an optical phase shifting section is usually required to adjust the phase shift between optical waveguides such that the interference between these waveguide outputs results in the formation of the required higher order mode (Weijin and Chiang 2018, 2016; Yang et al. 2015). Phase shifters are also essential sections in the phased arrayed (PHASAR) waveguide grating structures which are key elements in wavelength division multiplexing applications (Yang et al. 2015).

The phase shift acquired by a mode in a waveguide depends mainly on the length of the guide and the mode propagation constant. Using a specific technology platform, with specific refractive index distribution, the phase difference between two waveguides can be adjusted either by controlling the guide length or the guide width (which leads to a change in the propagation constant).

In Chaen et al. (2015), the phase shift is introduced between two similar waveguides by simply increasing the length of one guide with respect to the second one. This usually requires the use of a bending structure such that one of the guides becomes longer than the other. In Othman et al. (2008) the phase shift between the arrayed waveguides is controlled by using periodic segmented waveguide along the propagation direction. Inserting this arrayed grating between two Multimode Interference MMI structures used as splitters and combiners allows building a complete Straight PHASAR structure without bending. In El-Sabban and Khalil (2016), the phase shift between the two guides is introduced by changing the width of one guide leading to a change in its propagation constant. In Uematsu et al. (2012), the phase shift is also introduced a width change that varies with propagation direction to achieve a smooth transition. As a result, a phase shifter with butterfly-shape is used to construct a multiplexer for two TM modes. In Truong et al. (2019) and Tran et al. (2018), the butterfly shaped phase shifter is also to convert the fundamental mode TE0 to the 1st order mode TE1 and the 2nd order mode TE2 to the fundamental mode TE0. Similarly, in Qiu et al. (2015), the butterfly-shaped phase shifter is used in the conversion of the mode TE0 to the mode TE2.

In Rubana et al. (2017), the phase shifter is used as a part of mode switch to select one of the two outputs; TE0 mode or TE1. In Wageeh et al. (2018, 2020) the phase shifter with a butterfly-shape is used in the design of a 2D mode converter to enable the excitation of the LP21 fiber mode.

A brief of the phase shifter designs and their performance parameters is summarized in table (1) below. This table contains the technology used for each design, the length and width of phase shifter used and the overall insertion loss extracted in dB.

In this work we develop design formulas for the optical phase shift between two waveguides of the same length, one is used as a reference guide and the other creates the required phase change. The reference waveguide is assumed to have a fixed cross section that does not change with the propagation direction while the second guide (considered here as the “phase shifter” has a cross section that could be fixed or vary with the propagation direction). The different phase shifter configurations are studied with the objective of developing an analytical simple formula to facilitate its design. We analyze the case of single mode and multimode waveguides and develop the required approximations for the different configurations used for the phase shift generation. The condition of equal length for the two guides is used to avoid the bending of the overall integrated optical structure as in most of the PHASAR traditional designs. Analytical expressions are developed for each case and tested with respect to the numerical calculations carried out using the Beam Propagation Method BPM as a bench mark technique. The creation of a phase shift between two waveguides is tested by the excitation of the odd mode in a symmetric Y junction and thus the null output of the junction is used as an indication of a phase difference of π between the two guides. The case of step index guide is considered in our analysis. Section 2 describes the theoretical analysis used to calculate the phase shift between two waveguides and how this is used for the phase shifter design, in the single mode and multimode operation. In Sect. 3 we assume the waveguide width to be constant. In Sect. 4 the analysis is extended to the case of a tapered structure. Conclusion and references are introduced in Sects. 5 and 6 respectively.

2 Theoretical analysis

The simplest way to create a phase difference between two waveguides having the same length is to create a difference in the guiding properties of the waveguides such that each guide have a different propagation constant for the mode propagating into it. This leads directly to a phase difference Δφ between the two waveguides which is simply ΔβL where L is the length of the two guides. If the waveguide width or refractive index is slowly varying with z, an accumulated phase difference between the two guides can be expressed as (Truong et al. 2019):

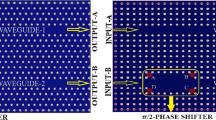
$$ \Delta \varphi = \mathop \int \limits_{0}^{L} \Delta \beta \left( z \right)dz = \mathop \int \limits_{0}^{L} \left( {\beta_{1} - \beta_{0} \left( z \right)} \right)dz $$
(1)

where Δβ(z) is the difference between the propagation constants of the two guides, β1 is the propagation constant of the guide “1” (that might be considered as a reference guide) and β0(z) is the propagation constant of the local normal mode of the guide 0 at the cross section z. For simplicity, which is also matching the typical practical designs, we will assume that the design is mainly focusing on the second waveguide to create the required phase difference. This guide with β1 is thus considered as our reference guide while the second guide is considered as the “phase shifter guide” as shown in Fig. 1.

Fig. 1
figure 1

Two waveguides: a reference guide with fixed width and specific z

Full size image

To examine the analytical results that will be developed in this work we will consider the typical Si photonic waveguide with the cross section shown in Fig. 2 with Si refractive index n1 = 3.474 surrounded by SiO2 of refractive index n0 = 1.444. The testing will be done at the operating wavelength λ = 1.55 µm unless otherwise specified.

Fig. 2
figure 2

2D Waveguide cross section structure

Full size image

For the analysis of this waveguide, the effective index method can be used to transform the 2D structure into an equivalent 1 D structure. Assuming all the waveguides to be fabricated with the same technology, and the same depth “d”, the geometrical design of the phase shifter is mainly focusing on the width of the guide “w”. The relation between the width “w” and the propagation constant of the guide needs thus to be expressed in an analytical formula to allow the design simplification.

For single mode waveguide, we can relate the fundamental mode effective index to its thickness through the normalized parameters V (normalized frequency) and b (normalized propagation constant) of the guide. For this purpose, we use the curve fitting for the linear region of the fundamental mode V-b relation shown in Fig. 3 in the range 0.3 < V < 3. This curve fitting allows describing the normalized propagation constant b as:

$$ b = \frac{{n_{eff}^{2} - n_{0}^{2} }}{{n_{1}^{2} - n_{0}^{2} }} = a_{1} V + a_{2} $$
(2)

where neff is the effective refractive index, n1 and n0 are the refractive indices of the guide and the surrounding medium respectively, a1, a2 are constants calculated from the curve fitting to be: a1 = 0.25 and a2 = − 0.06,\(V=\frac{2\pi }{\lambda }w\sqrt{{n}_{1}^{2}-{n}_{0}^{2}}\), and w is the guide width.

Fig. 3
figure 3

V-b relation for the fundamental mode in a waveguide and its linear fitting in the range 0.3 < V < 3

Full size image

From Eq. 2 the propagation constant β may be described as:

$$ \beta = \frac{2\pi }{\lambda } n_{eff} = \frac{2\pi }{\lambda }\sqrt {\frac{2\pi \cdot w}{\lambda }A + B} $$
(3)

where:

$$ \begin{gathered} A = \left( {n_{1}^{2} - n_{0}^{2} } \right)^{1.5} a_{1} \hfill \\ B = n_{0}^{2} + a_{2} \left( {n_{1}^{2} - n_{0}^{2} } \right) \hfill \\ \end{gathered} $$
(4)

On the other hand, for Multimode waveguide operation, the V-b relation of the waveguide cannot be approximated by the linear fitting and it is more appropriate to use a parabolic approximation. The propagation constant of the guide fundamental mode can be thus described using (Elrefai and Khalil 1997):

$$ \beta = k_{0} n_{g} - \frac{{\pi \lambda_{0} }}{{4n_{g} w^{2} }} $$
(5)

with ng the guide refractive index and W the guide width.

3 Two waveguide with constant widths

3.1 Single mode Waveguide

The first simple case to consider in our analysis is the case of two guides with fixed different widths w1 and w0, as shown in Fig. 4. In this case, each waveguide has a specific fixed effective refractive index neff1 and neff0 respectively and a propagation constant β1 and β0. The phase difference between the two waveguides after propagating a length L may be described from Truong et al. (2019) as:

$$ \Delta \emptyset = \mathop \int \limits_{0}^{L} \Delta \beta \left( z \right)dz = \mathop \int \limits_{0}^{L} \left( {\beta_{1} - \beta_{0} } \right)dz = \frac{2\pi }{\lambda }L\left[ {n_{eff1} - n_{eff0} } \right] $$
(6)

where neff1,neff0 are the effective refractive indices of waveguide 1 and 0 respectively (Table 1).

Table 1 The literature review results
Full size table
Fig. 4
figure 4

Two waveguides with different widths and a length L

Full size image

When the two guides are single mode guides, we can use Eqs. 2, 3 and 6; to express the phase difference as:

$$ \Delta \emptyset = \frac{2\pi }{\lambda }L \left[ {\sqrt {\frac{2\pi }{\lambda }Aw_{1} + B} - \sqrt {\frac{2\pi }{\lambda }Aw_{0} + B} } \right] $$
(7)

where A and B are the coefficients defined by Eq. 4.The phase shifter length L required to create a phase shift of Δφ can thus be calculated from Eq. 7:

$$ L = \frac{\lambda \Delta \emptyset }{{2\pi \left[ {\sqrt {\frac{2\pi }{\lambda }Aw_{1} + B} - \sqrt {\frac{2\pi }{\lambda }Aw_{0} + B} { }} \right]}} $$
(8)

Equation 8 represents an analytical design equation that can be used for the design of the phase shifter. The design parameters are L, w1 and w0 for a given guide with specific refractive index distribution represented by the coefficients A and B.

When the difference w1 – w0 = δw increases, the necessary length of the phase shifter, required to get a specific phase shift Δφ, is expected to be reduced. To examine this equation, we consider the standard single mode(SM) waveguide represented in Fig. 2. With w1 = 0.2 µm (corresponding to a normalized frequency V = 2.56 as described with vertical line in Fig. 3) to ensure single mode operation. Then, we can calculate the length required to get a phase shift π evaluated by Eq. 8 and compare it to the length estimated using the Beam Propagation Method BPM. For the length estimation by the BPM we consider the Mach–Zehnder structure shown in Fig. 5 where our reference waveguide of width w1 is the reference arm while the second arm has a width w0. The change of w0 allows examining this relation for the different lengths required to get the phase shift π for each w0. However, instead of plotting L as a function of w0 we plot it as a function of the difference δw = (w1 − w0).

Fig. 5
figure 5

A Mach Zehnder structure composed of 2 Y junctions connected by two straight waveguides with different widths w1 for the reference guide and w0 for the guide under test

Full size image

The results are illustrated in Fig. 6 and we can see that we have perfect matching between the two results. The difference between the analytical and numerical results is less than 96 nm (1.59% error percentage) in the range of δω from 20 to 180 nm. It should be noted here that the above relation is limited to SM waveguide within the range of validity of the V-b approximation used in Eq. 2. The BPM simulation setup is introduced in Table 2.

Fig. 6
figure 6

Phase Shifter length versus δw for two SM waveguides with constant widths

Full size image
Table 2 The BPM simulation setup
Full size table

3.2 Multimode waveguide

It is also possible to design the phase shifter using a multimode waveguide structure. This allows handling more power using the waveguide fundamental mode in each guide. The propagation constant of the guide fundamental mode can be thus described using Eq. 5:For the modes in the guide 1 (the reference guide) and the guide 0 (the phase shifter guide) respectively. This allows writing the difference between the two propagation constants of the modes as:

$$ \beta_{1} = k_{0} n_{g} - \frac{\pi \lambda }{{4n_{g} w_{1}^{2} }}{\kern 1pt} \quad \beta_{0} = k_{0} n_{g} - \frac{\pi \lambda }{{4n_{g} w_{0}^{2} }} $$
$$ \Delta \beta = \frac{{\pi \lambda_{0} }}{{4n_{g} }}\left[ {\frac{1}{{w_{0}^{2} }} - \frac{1}{{w_{1}^{2} }}} \right] $$
(9)

And thus from Eq. 1, the phase difference is:

$$ \Delta \emptyset = \frac{{\pi \lambda_{0} L}}{{4n_{g} }}\left[ {\frac{1}{{w_{0}^{2} }} - \frac{1}{{w_{1}^{2} }}} \right] $$
(10)

Based on that simple analysis, the phase shifter length required to create a phase shift of π between the two guides if we use Eq. 10 and take Δφ = π takes the form:

$$ L = \frac{{4n_{g} }}{{\lambda_{0} }} \frac{{w_{0}^{2} w_{1}^{2} }}{{\left( {w_{1}^{2} - w_{0}^{2} } \right)}} $$
(11)

Now to examine this relation, we consider the same case presented in Fig. 4 but with a waveguide width w1 = 0.65 µm for the reference guide while changing the guide width for the second guide from 0.05 to 0.6 µm which corresponds to changing the width difference δw from 0.6 to 0.05. The two waveguides are then inserted in the Mach –Zehnder configurations illustrated in Fig. 5 again and tested for the length required to create the phase shift of π, i.e. the length required to cancel or minimize the output of the MZ. The results obtained by both the analytical formula of Eq. 11 and the BPM calculations are shown in Fig. 7. Again, a very good agreement can be observed even for the values of δw for which the phase shifter waveguide becomes single mode while the reference guide is still multimode (MM).

Fig. 7
figure 7

Phase Shifter length versus δw for two MM waveguides with constant widths

Full size image

The difference between the analytical and numerical results here is less than 3 µm (8% error percentage) in the range of δω from 50 to 600 nm.

3.2.1 Phase shifter associated losses

The phase shifter consisting of a step in the waveguide width is the simplest phase shifter design. It can be easily implemented in the integrated optical technology through the control of the guide thickness in the mask layout; however, this sudden change in the guide width may also lead to some associated losses. For small width change (long phase shifter) the losses are usually negligible. An evaluation of this coupling loss between two waveguides with different widths is illustrated in Fig. 8, using the BPM calculation where the coupling between the powers launched into the fundamental mode of a waveguide of width 200 nm to the fundamental mode of a guide of width W is calculated. This coupling reflects essentially the overlap between the two modes and thus results in a significant loss when the difference in the mode extension increases. Such power loss can also affect the functionality of the optical circuit depending on the phase difference between two guides. To illustrate this effect, we consider the Mach Zehnder circuit shown in Fig. 5 with a slight difference between the two waveguides of the two arms δw = 20 nm, that is with the waveguide has a width w0 = 180 nm and the reference guide has a width of 200 nm. In this case, our analytical formula gives a length of 9.28 µm for the length required to create a phase shift of π between the guides which means that at this length, the output of the MZ interferometer should be cancelled. We then calculate the output of the interferometer over the C and L band from λ = 1480 nm to λ = 1620 nm. To evaluate how the output is deviated from its zero level we calculate the quantity G as:

$$ G = \left[ {1 - \frac{{P_{out} }}{{P_{in} }}} \right] $$

where Pout is the output power of the interferometer and Pin is its input power. When the losses are negligible, the two arms of the interferometers have the same power and we can easily show that:

$$ G = 1 - \cos^{2} \left( {\frac{\Delta \emptyset }{2}} \right) $$
(12)

with δW the phase shift introduced by the phase shifter due to the step in the waveguide width δW.

Fig. 8
figure 8

Coupling from a waveguide with a width of 200 nm to a waveguide with width W

Full size image

The calculations of G using the BPM and the analytical expression are shown in Fig. 9 when the losses are neglected in the analytical expression. A very good agreement can be observed. Here, the difference between the analytical and numerical results here is less than 0.01% in the range of wavelength from 1480 to 1620 nm. As the guides are single mode in this case, we use Eqs. 3, 4, and 7 for the calculations.

Fig. 9
figure 9

The quantity G (1-Normalized Output Power) as a function of the wavelength for a phase shifter with step discontinuity in SM waveguide

Full size image

Figure 10 shows the power reflection coefficient Γ2 for this SM transition as a function of the step in the width δw calculated using the FDTD (Finite Difference Time Domain) technique. It shows clearly the increase of the reflected power as we increase the difference between the two waveguides.

Fig. 10
figure 10

Power reflection coefficient calculations as a function of δw for a SM Si/SiO2 waveguide with w1 = 200 nm and w0 is changing from 10 to 180 nm

Full size image

The results in Fig. 10 indicate the main drawback of using a simple step discontinuity for creating the required phase shift. The step discontinuity results in losses and reflections. The multiple reflections between the two discontinuities may also results in a Fabry–Perot effect, and hence in some fluctuations in the response as a function of the wavelength. In addition, the amount of power lost from the fundamental mode in this discontinuity may also be coupled to higher order modes, either higher order guided modes or radiation modes. The FDTD simulation setup is introduced in Table 3.

Table 3 The FDTD simulation setup
Full size table

The propagation of these modes in the structure may also affect the functionality of the device. This depends on the radiation mode spectrum and its coherence coupling in the structure (Gérard et al. 1994; Khalil and Tedjini 1992).

These losses and higher mode coupling are usually the motivations of the use of a tapered structure for the phase shifter guide. This structure will be considered in the next section.

4 Tapered phase shifter structure

To avoid the reflections and radiation losses or power coupling to higher order guided modes due to the step discontinuity in the waveguide width, a tapering structure can be used to create the phase shift in the waveguide “phase shifter”.

4.1 Linear tapered single mode waveguide shifter

In this case, we consider a linear tapered SM waveguide used as a phase shifter (Duport et al. 1992). The configuration of the reference and phase shifter guides are thus as shown in Fig. 11. The required phase shift is achieved through two sections of the taper structure mirrored around its center as shown in Fig. 11. In a first configuration we assume that the two waveguides are Single Mode (SM).

Fig. 11
figure 11

Two SM waveguides: the first guide has a constant width, and the second guide is composed of two mirrored tapered sections with a width changing linearly from w1 to w0

Full size image

The first waveguide is starting with a width (w1) which is linearly changing to decrease to a width w0 at half the length of the structure Lhalf = L/2 while the reference waveguide is keeping a constant width (w1) as shown in Fig. 11.The phase shift between the two guides can be expressed like Eq. 1 if the shape of waveguide is symmetric around the center of w.g length (Lhalf) as:

$$ \Delta \emptyset = 2 \mathop \int \limits_{0}^{{L_{half} }} \Delta \beta \left( z \right)dz $$
(13)

where we assume that the waveguide is an adiabatic transition and β(z) is the propagation constant of the local normal mode of the guide at the cross-section z. From Eq. 3, the propagation constant at z can be expressed as:

$$ \beta \left( z \right) = \frac{2\pi }{\lambda }n_{eff} \left( z \right) = \frac{2\pi }{\lambda } \sqrt {\frac{2\pi w\left( z \right)}{\lambda }A + B} $$
(14)

where w(z) can be described with the linear distribution as shown in Fig. 11 as:

$$ w\left( z \right) = w_{1} - \frac{1}{{L_{half} }}\left( {w_{1} - w_{0} } \right)z $$
(15)

Using Eqs. 15 into 14 to calculate the phase difference in Eq. 13, we get the phase difference Δφ in the form:

$$ \Delta \emptyset = \frac{2\pi }{\lambda }L\left[ { \frac{2}{{3C_{2} }}\left( {C_{1}^{1.5} - \left( {C_{1} - C_{2} } \right)^{1.5} } \right) - n_{eff0} } \right] $$
(16)

With

$$ C_{1} = \frac{2\pi }{\lambda } A w_{1} + B\quad C_{2} = \frac{2\pi }{\lambda } A\left( {w_{1} - w_{0} } \right) $$
(17)

where the coefficients A and B defined above in Eq. 4 are used again to express the guiding properties of the waveguide.

Equation 16 allows the design of a linear tapered section to create the required phase shift between the reference and the phase shifter waveguides. To examine this equation, we consider again the MZ configuration of Fig. 5 where the phase shifter is replaced by the tapered structure. The MZ takes the form of Fig. 12.The reference SM waveguide has a width w1 = 200 nm (V = 2.56) to ensure single mode operation. The phase shifter smaller width changes and its change is expressed by the parameter δw = w1 − w0 that varies from 20 to 184 nm. We calculate the length required for a phase shift of π using both the analytical expression and the BPM. The results are illustrated in Fig. 13 where a good agreement can be observed. In this case, the difference between the analytical and numerical results here is less than 1.5 µm in the range of δω from 30 to 190 nm.

Fig. 12
figure 12

A Mach Zehnder structure composed of 2 Y junctions connected by two waveguides. First guide is the reference straight guide with width w1 and the second guide is the guide under test composed of two sections of a linear tapered guide with a width changing from w1 to w0

Full size image
Fig. 13
figure 13

Phase Shifter length versus δw for SM waveguide case

Full size image

4.2 Linear tapered multi mode waveguide shifter

In this section we examine the case where the phase shifter guide could be a MM linear tapered waveguide. In this case, the reference guide has a width w1 and the phase shifter guide has a width that changes linearly from w1 to w0 and again to w1 to avoid the step discontinuity in the guide, however we allow the guide to be MM. The propagation constant in the MM waveguide is approximated by the expressions given in Eq. 5, however in this case we have β = β (z). Using the adiabatic relation described in 9, we get:

$$ \Delta \beta \left( z \right) = \frac{{\pi \lambda_{0} }}{{4n_{g} }}\left[ {\frac{1}{{w^{2} \left( z \right)}} - \frac{1}{{w_{1}^{2} }}} \right] $$

and then from equation 13 , Δφ is given from by:

$$ \Delta \emptyset = \frac{{\pi \lambda_{0} L}}{{4n_{g} }}\left[ {\frac{{w_{1} - w_{0} }}{{w_{0} w_{1}^{2} }}} \right] $$
(18)

The derivation of Eq. 18 is introduced in Appendix.

From equation 18, the taper length required to get a phase shift of π can be easily calculated as:

$$ L = \frac{{4n_{g} }}{{\lambda_{0} }}\left[ {\frac{{w_{1}^{2} w_{0} }}{{w_{1} - w_{0} }}} \right] $$
(19)

For w1 = 0.65 µm and δw varying from 0.02 to 0.4 µm, the length calculated by equation 19 is plotted in Fig. 14 in comparison with the results obtained by the BPM. Again a very good agreement can be easily observed. The difference between the analytical and numerical results here is less than 13.7 µm in all the range of δω from 40 nm to 400 nm.

Fig. 14
figure 14

Phase Shifter length versus δw for MM waveguide case

Full size image

5 Conclusion

In this work, we developed analytical expressions for the design of an optical phase shifter waveguide. The analytical forms are developed for both the step change in the guide width as well as the linear tapered change in the guide width for both SM and MM operation. The Obtained results are compared with the BPM numerical calculations and a good agreement is observed. These expressions are validated for the case where the discontinuity losses are relatively small and can be neglected. While these expressions have been developed for a step index waveguide, they can be easily extended for other type of waveguides using suitable approximations for the waveguide dispersion relation.