Teleportation two-qubit state by using two different protocols

Abstract

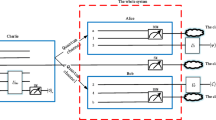
In this contribution, two versions of teleportation protocol are considered, based on either using a single or two copies of entangled atom-field state, respectively. It is shown that, by using the first version, the fidelity of the teleported state as well as the amount of quantum Fisher information, that contains in the teleported state, are much better than using the second version. In general, one may increases the fidelity of teleported information by increasing the mean photon number and decreasing the detuning parameter. The fidelity of teleporting classical information is much better than teleporting quantum information. Moreover, teleportating classical information that initially encoded in an exited states is much better than that encodes in the ground states. However, the teleported Fisher information that initially encoded in a ground state is much larger than those initially encoded in entangled states.

Appendix

The coefficients $\alpha _{i}$ ($i=0,\ldots ,5$) are obtained from Eq. (4) as

$$\begin{aligned} \alpha _{1}&= {} \frac{P_{n-1}^{2}}{{\mathcal {N}}}\frac{n}{\delta ^2+n}\sin ^{2}(\tau \sqrt{\delta ^2+n}), \nonumber \\ \alpha _{2}= &\, {} \frac{P_{n}^{2}}{{\mathcal {N}}}\Big [\cos ^{2}(\tau \sqrt{\delta ^2+(n+1)})+ \frac{\delta ^{2}}{\delta ^2+(n+1)}\sin ^{2}(\tau \sqrt{\delta ^2+(n+1)})\Big ], \nonumber \\ \alpha _{3}= &\, {} i\frac{P_{n}^{2}\sqrt{n+1}e^{-i\delta \tau }}{{\mathcal {N}} \sqrt{\delta ^2+(n+1)}}\sin (\tau \sqrt{\delta ^2+(n+1)}) \Bigl [\cos (\tau \sqrt{\delta ^2+(n+1)}) \nonumber \\&-\,i\frac{\delta \sin (\tau \sqrt{\delta ^2+(n+1)})}{\sqrt{\delta ^2+(n+1)}}\Bigr ],\nonumber \\ \alpha _{4}= &\, {} \frac{P_{n}^{2}}{{\mathcal {N}}}\frac{(n+1)}{\delta ^2+(n+1)}\sin ^{2}(\tau \sqrt{\delta ^2+(n+1)}),\nonumber \\ \alpha _{5}= &\, {} \frac{P_{n+1}^{2}}{{\mathcal {N}}}\Bigl [\cos ^{2}(\tau \sqrt{\delta ^2+(n+1)})+ \frac{\delta ^2}{\delta ^2+(n+1)}\sin ^{2}(\tau \sqrt{\delta ^2+(n+1)})\Bigr ], \end{aligned}$$

(17)

where $\delta$ is the dimentionless detuning and the normalization of the state ${\mathcal {N}}$ is given by,

$$\begin{aligned} {\mathcal {N}}&= {} P_{n}^{2}+ \Bigl [\frac{n}{\delta ^2+n}\sin ^{2}(\tau \sqrt{\delta ^2+n})\Bigr ]P_{n-1}^2\nonumber \\&+\,\Bigl [\cos ^{2}(\tau \sqrt{\delta ^2+(n+1)})+\frac{\delta ^2}{\delta ^2+(n+1)}\sin ^{2}(\tau \sqrt{\delta ^2+(n+1)})\Bigr ]P_{n+1}^{2}. \end{aligned}$$

(18)