1 Introduction

Since the quantum key distribution (QKD) protocol, first raised in 1984 (Bennett and Brassard 1984), has been paid great attention to by the researchers all over the world, due to its unique secure long distance key distribution. Thus a lot of studies, both in theory and experiment have been done to improve its technology. So far, secure key distribution has been achieved both in fiber channel and free space channel (Ketaki et al. 2013). The researches have shown that it is the most efficient global network QKD scheme, where satellite-earth links used as the core line for long distance distribution and ground fiber network as the auxiliary line for short distance.

It is known that the key rate of the satellite-earth quantum key distribution is very low, owing to its great loss. Thus different attempts have been done to increase the rate. Decoy state might raise single channel rate by increasing mean photon number in a single pulse, the system security can be guaranteed through pulses of different intensities (Manderbach et al. 2007). Wavelength division multiplex could raise the key rate by increasing the channel numbers at the same time. It is necessary to equip an independent optical source and modem for every quantum channel, which is almost unacceptable for the limited satellite load (Yoshino et al. 2012). Single-photon multi-qubits state is supposed to increase the quantum channel transmission speed effectively (Gu-hao et al. 2013), but the different quantum states of a single photon cannot transmit steadily in the same channel. In the subcarrier multiplexing QKD based on polarization coding (Gu-hao et al. 2013), the key could be shared by several parallel sideband channels, and each sideband has a random and independent polarization which is synthesized by controlling the phase difference of subcarriers in two electro-optical phase modulators. Though the key could be increased theoretically, it is probably difficult to put it in daily application owing to the employment of a broadband radio frequency signal combiner.

We present a parallel QKD scheme based on M–Z interferometer, which can fulfill multi-channel parallel quantum key distribution only with the actually available devices.

2 System composition and theoretical derivation

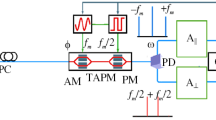
The diagram of double arm M–Z interferometer is shown in Fig. 1.

Fig. 1
figure 1

Diagram of double arm M–Z interferometer

Full size image

Here, \(V_i (t)=V_{dci} +V_{RFi} \cos (\omega _i t+\phi _i )\), is RF driving signals of the interferometer modem, \(V_{dci} \)—the DC bias voltage, \(V_{RFi} \)—RF signal amplitude, \(\phi _i \)—RF signal phase. When we set input optical signal as \(E_{in} (t)=E_0 e^{i\omega _0 t}\), the output optical field of the M–Z interferometer can be expressed as,

$$\begin{aligned} E_{MZM} (t)=\frac{\sqrt{2}E_0 }{2}\left\{ {\exp \left( {j\frac{\pi V_1 \left( t \right) }{V_\pi }} \right) +\gamma \exp \left( {j\frac{\pi V_2 \left( t \right) }{V_\pi }} \right) } \right\} e^{i\omega _0 t} \end{aligned}$$
(1)

Here, \(V_\pi \)—half-wave voltage of the M–Z interferometer, \(\gamma \)—shunt coupling ratio. Suppose the coupling ratio \(=\) 1, we design the two channel subcarrier multiplexing quantum key distribution scheme based on polarization encoding phase synthesis of the M–Z interferometer (Fig. 2).

Fig. 2
figure 2

The two channel subcarrier multiplexing quantum key distribution scheme based on M–Z interferometer

Full size image

In this scheme, the laser output is modulated to \(45^{\circ }\) polarized light, and divided into two orthogonal polarized optical signal by a polarization beam splitter. The optical light is modulated separately through \(\hbox {VCO}_{1}\) and \(\hbox {VCO}_{2}\), and the lithium niobate modulator is replaced by two M–Z interferometers. Output RF signal of the \(\hbox {VCO}_{1}\) is equally divided into two. One is to be modulated through \(\hbox {M--Z}_{2}\) up-arm without phase modulation, the other is to be modulated through \(\hbox {M--Z}_{1}\) up-arm after adjusted by the phase controller \(\varPhi _{1.}\) In the same way, output RF signal of the \(\hbox {VCO}_{2}\) is equally divided into two. One is to be modulated through \(\hbox {M--Z}_{2}\) lower-arm without phase modulation, the other is to be modulated through \(\hbox {M--Z}_{1}\) lower-arm after adjusted by the phase controller \(\varPhi _{2}\). The two modulated optical signals are mixed by a polarization bean combiner.

Each arm of the M–Z interferometer can be regarded as an independent LiNbo3, there are subcarrier RF signals input through both of them. Suppose the photon polarization in y direction line of Route 1 is marked as \(\left| y \right\rangle \), x direction line of Route 2 is marked as \(\left| x \right\rangle \), then the composite signals of the two M–Z interferometers can be expressed as,

$$\begin{aligned} \left| {E_{out} } \right\rangle&= E_{M-Z1} \left| y \right\rangle +E_{M-Z2} \left| x \right\rangle \nonumber \\&= \frac{\sqrt{2}}{2}jE_0 e^{j\omega _0 t}e^{\frac{j\pi V_{dc} }{V_\pi }}\left[ \left( 1+\sum _{p=1}^n {\frac{\left( {m\frac{1}{2}(e^{j(\omega _1 t)}+e^{-j(\omega _1 t)})} \right) ^{p}}{p!}} \right) \left| y \right\rangle \right. \nonumber \\&\quad \left. +\,\left( 1+\sum _{p=1}^n {\frac{\left( {m\frac{1}{2}(e^{j(\omega _1 t+\phi _1 )}+e^{-j(\omega _1 t+\phi _1 )})} \right) ^{p}}{p!}} \right) \left| x \right\rangle \right] \nonumber \\&\quad +\,\frac{\sqrt{2}}{2}jE_0 e^{j\omega _0 t}e^{\frac{j\pi V_{dc} }{V_\pi }}\left[ \left( 1+\sum _{p=1}^n {\frac{\left( {m\frac{1}{2}(e^{j(\omega _2 t)}+e^{-j(\omega _2 t)})} \right) ^{p}}{p!}} \right) \left| y \right\rangle \right. \nonumber \\&\quad \left. +\,\left( 1+\sum _{p=1}^n {\frac{\left( {m\frac{1}{2}(e^{j(\omega _2 t+\phi _2 )}+e^{-j(\omega _2 t+\phi _2 )})} \right) ^{p}}{p!}} \right) \left| x \right\rangle \right] \end{aligned}$$
(2)

Carrier frequency signal extracted from composite signal can be marked as,

$$\begin{aligned} \left| {E_{\textit{carrier}} } \right\rangle =\frac{\sqrt{2}}{2}jE_0 e^{i\omega _0 t}e^{\frac{j\pi V_{dc} }{V_\pi }}\left( {\left| x \right\rangle +\left| y \right\rangle } \right) \end{aligned}$$
(3)

From the equation above, we may find that carrier frequency polarization state is free from the phase information of the RF signal. So we may conclude that the carrier frequency polarization state of the output optical signal is always \(45^{\circ }\) polarized light, regardless of the RF subcarrier phase position. The polarization of first sideband signal extracted from the composite signal can be expressed as,

$$\begin{aligned} \left| {E_{out\_first} } \right\rangle&= E_{M\hbox {--}Z1} \left| y \right\rangle +E_{M\hbox {--}Z2} \left| x \right\rangle \nonumber \\&= \frac{\sqrt{2}}{2}jE_0 e^{\frac{j\pi V_{dc} }{V_\pi }}\left[ \frac{m}{2}e^{j(\omega _0 +\omega _1 )t}(\left| x \right\rangle +e^{j\varphi _1 }\left| y \right\rangle )\right. \nonumber \\&\quad \left. +\,\frac{m}{2}e^{j(\omega _0 -\omega _1 )t}(\left| x \right\rangle +e^{-j\varphi _1 }\left| y \right\rangle ) \right] \nonumber \\&\quad +\,\frac{\sqrt{2}}{2}jE_0 e^{\frac{j\pi V_{dc} }{V_\pi }}\left[ \frac{m}{2}e^{j(\omega _0 +\omega _2 )t}(\left| x \right\rangle +e^{j\varphi _2 }\left| y \right\rangle )\right. \nonumber \\&\quad \left. +\,\frac{m}{2}e^{j(\omega _0 -\omega _2 )t}(\left| x \right\rangle +e^{-j\varphi _2 }\left| y \right\rangle ) \right] \end{aligned}$$
(4)

There are four frequencies, i.e. \(\omega _{0}\,\pm \,\omega _{1}, \omega _{0}\,\pm \,\omega _{2}\) in the first sideband, and their polarization states are controlled by RF phase difference \(\phi _i \). When \(\phi _i \) changes continuously from 0 to 2\(\pi \), their output polarization states change continuously from \(45^{\circ }\) polarization—right circular polarization—\(135^{\circ }\) polarization—left circular polarization too. These four polarization states can meet the requirement of polarization in BB84 Protocol. Similarly, the sideband polarization could be controlled by the RF phase difference in the second sideband, which served also as quantum channel.

3 System bit error rate

3.1 Intermodulation bit error

During the process of a subcarrier multiplexing quantum key distribution and modulation, cross modulation interference may occur when the frequencies of the two sidebands with different polarization state are the same or very similar (Xuemin and Shuqiang 1999; Chu and Gans 1991). According to the principles of Quantum Mechanics, the measurement result is probable, when a polarization vector is measured on a nonopiate polarization vector bases. So intermodulation is the main origin of the bit error. The drop shadow of the signal sideband polarization of the intermodulation sideband polarization is expressed as,

$$\begin{aligned} \left| \psi \right\rangle&= \left| {\psi _{signal} } \right\rangle \left\langle {\psi _{signal} } \right| \left| {\psi _{noise} } \right\rangle \nonumber \\&= \frac{1}{2}\left( {\left| x \right\rangle +e^{i\varphi _s }\left| y \right\rangle } \right) \left( {\left\langle x \right| +e^{-i\varphi _s }\left\langle y \right| } \right) \cdot \frac{\sqrt{2}}{2}\left( {\left| x \right\rangle +e^{i\varphi _n }\left| y \right\rangle } \right) \nonumber \\&= \frac{1}{2}\left( {1+e^{i\left( {\varphi _n -\varphi _s } \right) }} \right) \left| {\psi _{signal} } \right\rangle \end{aligned}$$
(5)

Here, bit error probability caused by intermodulation sidebands may be expressed as,

$$\begin{aligned} p_{IM} =1-\left( {\frac{\left( {1+e^{i\left( {\varphi _n -\varphi _s } \right) }} \right) }{2}} \right) ^{2} \end{aligned}$$
(6)

Four polarization states of the subcarrier multiplexing quantum key distribution and modulation appear with equal probability, i.e.. equal probability combination of signal sidebands with intermodulation sidebands. Then the bit error generated by the intermodulation sideband can be expressed as,

$$\begin{aligned} QBER=\sum _{\varphi _0 =0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}} {\sum _{\varphi _1 =0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}} {\frac{1}{16}\frac{p_{IM} P_{IM} }{P_S +P_{IM} }} } \end{aligned}$$
(7)

where, \(P_{IM }\)—power of intermodulation sideband, \(P_{S}\)—power of signal sideband.

3.2 Quantum bit error rate introduced by phase noise

Ideal laser source is a monochromatic coherent light with stable frequency. Because there is a spontaneous radiation of the laser device, that causes the phase fluctuation of output optical field and some linewidth occurs. So the phase fluctuation brings the phase noise (Drever et al. 1983; Henry 1983), that will worsen the modulation performance. Phase noise \(\varPhi (t)\) can be regarded as a Wiener process. Thus, with the help of theory deduction, the power spectral density(PSD)expression of the phase noise is expressed as Xiang-ke et al. (2008),

$$\begin{aligned} P_{ph} (\omega )=P_0 \frac{2}{\pi \Delta \omega }\frac{1}{1+\left( \frac{\omega -\omega _0 }{\Delta \omega /2}\right) ^{2}} \end{aligned}$$
(8)

where, \(P_{0 }\)—total power of the laser output pulse, \(\Delta \omega \)—full width half maximum value(3dB BW), \(\omega _{0}\)—center frequency of laser pulse. Phase noise of the laser device is the power intensity of the frequency near the center frequency, free from the process of subcarrier modulation. Suppose, the carrier polarization state is \(45^{\circ }\) polarized light, and it does not transform along with the RF subcarrier phase change. \(P_{ph}\)— the bit error probability of the phase noise polarization generated in the signal sideband polarization, can be expressed as,

$$\begin{aligned} p_{ph} =1-\left( {\frac{\left( {1+e^{i\varphi _0 }} \right) }{2}} \right) ^{2} \end{aligned}$$
(9)

Thus, the phase noise will increase QBER. The former equation (6) can be corrected by the application of the phase noise, so the amended quantum bit error rate can be expressed as,

$$\begin{aligned} QBER=\sum _{\varphi _0 =0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}} {\sum _{\varphi _1 =0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}} {\frac{1}{16}\frac{p_{IM} P_{IM} +p_{ph} P_{ph} }{P_S +P_{IM} +P_{ph} }} } \end{aligned}$$
(10)

where, \(P_{ph}\)—phase noise power of the signal frequency. Figure 3 is the Phase noise spectrum of laser source. In simulation, suppose the central \(\hbox {wavelength}=1{,}550\) nm, \(\Delta \omega =10\,\hbox {MHz}\), total power of the laser pulse \(\hbox {P}_{0}=10^{-3}\) W.

Fig. 3
figure 3

Phase noise spectrum of laser source

Full size image

In order to study the cross interference, the most severely interfered RF modulation signal frequency groups 10 and 20 GHz are selected intentionally. The intermodulation of signal sidebands when the first sideband 1,550 nm \(+\) 10 GHz and 1,550 nm \(+\) 20 GHz used as the signal channel, and the second sideband 1,550 nm \(+\) 30 GHz and 1,550 nm \(+\) 40 GHz used as the signal channel, is analyzed, and their corresponding laser device phase noise powers with \(-\)46.033 dBm (\(2.49\times 10^{-5}\) mW), \(-\)52.059 dBm (\(6.224\times 10^{-6}\) mW), \(-\)55.583 dBm (\(2.765\times 10^{-6}\) mW) and \(-\)58.083 dBm (\(1.555\times 10^{-6}\) mW). These noise power intensities are free from the modulation coefficient. And their polarization state is not controlled by the modulating signal phase difference. They are only in line with the carrier polarization. Figure 4 shows the quantum bit error rate simulation of subcarrier multiplexing QKD.

Fig. 4
figure 4

The quantum bit error rate simulation of subcarrier multiplexing QKD. a The quantum bit error rate when the first sideband 1,550 nm \(+\) 10 GHz is used as the signal channel. b The quantum bit error rate when the first sideband 1,550 nm \(+\) 20 GHz is used as the signal channel. c The quantum bit error rate when the second sideband 1,550 nm \(+\) 30 GHz is used as the signal channel. d The quantum bit error rate when the second sideband 1,550 nm \(+\) 40 GHz is used as the signal channel

Full size image

We may find out that the bit errors are always very large when the modulation coefficients are small. With the rise of the modulation coefficient, there comes a minimal point of the bit error rate, and that matches well with the former theoretical analysis. The four turning points in the Fig. 4 are set as 10 GHz (m \(=\) 0.08, QBER \(=\) 0.2439 %), 20 GHz(m \(=\) 0.11, QBER \(=\) 0.1224 %), 30 GHz(\(\hbox {m}=0.32\), QBER \(=\) 0.8045 %), 40 GHz(\(\hbox {m}=0.27\), \(\hbox {QBER}=2.21\) %). From the point of quantum bit error rate of the modulator, the first sideband 10 GHz and 20 GHz has some advantage over the other two, due to the origin of the optical signal, noise and signal intensity. The result of the theoretical calculation shows that the two first sidebands have the same signal power. But the one close to carrier center frequency has a higher phase noise power that will have some impact on the signal. So in a system where the first sideband is served as the signal sideband, it is better to choose the signal sideband frequency far away from the center frequency, the further, the better. The high order sideband is greatly affected by the noise and intermodulation, because it has a lower power. In a system where the high order sideband is served as the signal sideband, it is necessary to put the modulation power of the chosen signal sideband into consideration.

4 Conclusion

A subcarrier multiplexing QKD scheme based on M–Z interferometer is presented in this paper, where a parallel quantum key distribution is realized with the application of subcarrier multiplexing(SCM). Simulation calculation shows that the minimum bit error rate is below 0.25 or 2.21 % when the first sideband or the second sideband used as the signal sideband. Both could meet the BER requirement of the quantum key distribution.

This scheme can also implement a parallel quantum key modulation with less modulators as the one proposed in Gu-hao et al. (2013). Nevertheless, it is much more achievable than the one mentioned in Gu-hao et al. (2013), because the devices used are all actually available.