Abstract
This paper proposes a scenario sampling-based framework to estimate the expected incremental routing cost required so as to incorporate a target customer into an inherently stochastic supply chain network. Inspired from a real-life setting arising in the distribution of industrial gases, we demonstrate our framework and elucidate the quality of the marginal cost estimates it can provide by sampling instances of the multi-depot vehicle routing problems with inter-depot routes. In order to solve such rich routing problems exactly, we also develop a tailored branch-price-and-cut algorithm, which is shown to be able to solve to optimality instances of up to 70 customers within reasonable time, outperforming existing state-of-the-art methods. Our computational studies further provide insights to the effect that various factors related to the target customer and/or the overall network structure can generally have on the marginal routing costs.








Similar content being viewed by others
Notes
For example, having to perform a hazardous materials delivery to a downtown customer authorizes the vehicle to enter the downtown area in the first place, allowing it to then reach customers on the other side of the city without traversing the longer bypass route.
References
Angelelli E, Speranza MG (2002) The periodic vehicle routing problem with intermediate facilities. Eur J Oper Res 137(2):233–247
Augerat P, Belenguer J-M, Benavent E, Corbéran A, Naddef D (1998) Separating capacity constraints in the CVRP using tabu search. Eur J Oper Res 106(2–3):546–557
Baldacci R, Christofides N, Mingozzi A (2008) An exact algorithm for the vehicle routing problem based on the set partitioning formulation with additional cuts. Math Program 115(2):351–385
Baldacci R, Mingozzi A, Roberti R (2011) New route relaxation and pricing strategies for the vehicle routing problem. Oper Res 59(5):1269–1283
Buhrkal K, Larsen A, Ropke S (2012) The waste collection vehicle routing problem with time windows in a city logistics context. Procedia Soc Behav Sci 39:241–254
Cattaruzza D, Absi N, Feillet D (2016) Vehicle routing problems with multiple trips. 4OR 14(3):223–259
Chaudhuri S, Motwani R, Narasayya V (1998) Random sampling for histogram construction: how much is enough? ACM SIGMOD Rec 27(2):436–447
Contardo C, Martinelli R (2014) A new exact algorithm for the multi-depot vehicle routing problem under capacity and route length constraints. Discrete Optim 12:129–146
Crevier B, Cordeau J-F, Laporte G (2007) The multi-depot vehicle routing problem with inter-depot routes. Eur J Oper Res 176(2):756–773
Daganzo CF (1984) The distance traveled to visit N points with a maximum of C stops per vehicle: an analytic model and an application. Transp Sci 18(4):331–350
de Aragao MP, Uchoa E (2003) Integer program reformulation for robust branch-and-cut-and-price algorithms. In: Mathematical program in Rio: a conference in Honour of Nelson Maculan. Citeseer, pp 56–61
Dror M (1994) Note on the complexity of the shortest path models for column generation in VRPTW. Oper Res 42(5):977–978
Feillet D (2010) A tutorial on column generation and branch-and-price for vehicle routing problems. 4OR 8(4):407–424
Figliozzi MA (2008) Planning approximations to the average length of vehicle routing problems with varying customer demands and routing constraints. Transp Res Rec 2089(1):1–8
Fukasawa R, Longo H, Lysgaard J, de Aragão MP, Reis M, Uchoa E, Werneck RF (2006) Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Math Program 106(3):491–511
Gibbons PB, Tirthapura S (2001) Estimating simple functions on the union of data streams. In: Proceedings of the thirteenth annual ACM symposium on parallel algorithms and architectures. ACM, pp 281–291
Hoeffding W (1994) Probability inequalities for sums of bounded random variables. In: The collected works of Wassily Hoeffding. Springer, Berlin, pp 409–426
Irnich S, Desaulniers G, Desrosiers J, Hadjar A (2010) Path-reduced costs for eliminating arcs in routing and scheduling. INFORMS J Comput 22(2):297–313
Jepsen M, Petersen B, Spoorendonk S, Pisinger D (2008) Subset-row inequalities applied to the vehicle-routing problem with time windows. Oper Res 56(2):497–511
Kim B-I, Kim S, Sahoo S (2006) Waste collection vehicle routing problem with time windows. Comput Oper Res 33(12):3624–3642
Kleywegt AJ, Shapiro A, Homem-de Mello T (2002) The sample average approximation method for stochastic discrete optimization. SIAM J Optim 12(2):479–502
Kone ER, Karwan MH (2011) Combining a new data classification technique and regression analysis to predict the cost-to-serve new customers. Comput Ind Eng 61(1):184–197
Laporte G, Nobert Y (1983) A branch and bound algorithm for the capacitated vehicle routing problem. Oper Res-Spektrum 5(2):77–85
Lübbecke ME, Desrosiers J (2005) Selected topics in column generation. Oper Res 53(6):1007–1023
Marchetti PA, Gupta V, Grossmann IE, Cook L, Valton P-M, Singh T, Li T, André J (2014) Simultaneous production and distribution of industrial gas supply-chains. Comput Chem Eng 69:39–58
Muter I, Cordeau J-F, Laporte G (2014) A branch-and-price algorithm for the multidepot vehicle routing problem with interdepot routes. Transp Sci 48(3):425–441
Özener OÖ, Ergun Ö, Savelsbergh M (2013) Allocating cost of service to customers in inventory routing. Oper Res 61(1):112–125
Pecin D (2014) Exact algorithms for the capacitated vehicle routing problem. Doctoral Dissertation, Pontifícia Universidade Católica do Rio de Janiero, Rio de Janiero, Brazil
Pecin D, Contardo C, Desaulniers G, Uchoa E (2017a) New enhancements for the exact solution of the vehicle routing problem with time windows. INFORMS J Comput 29(3):489–502
Pecin D, Pessoa A, Poggi M, Uchoa E (2017b) Improved branch-cut-and-price for capacitated vehicle routing. Math Program Comput 9(1):61–100
Pecin D, Pessoa A, Poggi M, Uchoa E, Santos H (2017c) Limited memory rank-1 cuts for vehicle routing problems. Oper Res Lett 45(3):206–209
Pessoa A, Sadykov R, Uchoa E, Vanderbeck F (2020) A generic exact solver for vehicle routing and related problems. Math Program 183:1–41
Pugliese LDP, Guerriero F (2013) A survey of resource constrained shortest path problems: exact solution approaches. Networks 62(3):183–200
Ramos Tânia Rodrigues, Pereira R, Gomes MI, Barbosa-Póvoa AP (2020) A new matheuristic approach for the multi-depot vehicle routing problem with inter-depot routes. OR Spectrum 42(1):75–110
Røpke S (2012) Branching decisions in branch-and-cut-and-price algorithms for vehicle routing problems. In: Presentation in column generation
Sadykov R, Uchoa E, Pessoa A (2021) A bucket graph-based labeling algorithm with application to vehicle routing. Transp Sci 55(1):4–28
Schiffer M, Schneider M, Walther G, Laporte G (2019) Vehicle routing and location routing with intermediate stops: a review. Transp Sci 53(2):319–343
Sun L, Karwan MH, Gemici-Ozkan B, Pinto JM (2015) Estimating the long-term cost to serve new customers in joint distribution. Comput Ind Eng 80:1–11
Tarantilis CD, Zachariadis EE, Kiranoudis CT (2008) A hybrid guided local search for the vehicle-routing problem with intermediate replenishment facilities. INFORMS J Comput 20(1):154–168
Toth P, Vigo D (2014) Vehicle routing: problems, methods, and applications. SIAM, Philadelphia
Turkensteen M, Klose A (2012) Demand dispersion and logistics costs in one-to-many distribution systems. Eur J Oper Res 223(2):499–507
Uchoa E, Pecin D, Pessoa A, Poggi M, Vidal T, Subramanian A (2017) New benchmark instances for the capacitated vehicle routing problem. Eur J Oper Res 257(3):845–858
Van der Vaart AW (2000) Asymptotic statistics, vol 3. Cambridge University Press, Cambridge
Acknowledgements
We thank Dr. Ibrahim Muter and Dr. Jean-François Cordeau for providing us with useful clarifications about the datasets that were utilized in their previous work. We acknowledge financial support from Air Liquide through the Center for Advanced Process Decision-making at Carnegie Mellon University. Akang Wang also greatly acknowledges support from the James C. Meade Graduate Fellowship and the H. William and Ruth Hamilton Prengle Graduate Fellowship at Carnegie Mellon University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A. Appendix
A. Appendix
1.1 A.1. Branch-price-and-cut algorithm for the MDVRPI
In the BPC algorithm, the LP relaxations at every node in the branch-and-bound tree are solved via column generation, while cutting planes are added to strengthen the relaxations. Our implementation incorporates and extends several elements of the algorithm described in Pecin et al. (2017b), including ng-routes (Baldacci et al. 2011), variable fixing (Irnich et al. 2010), route enumeration (Baldacci et al. 2008), and limited-memory subset row cuts (Pecin et al. 2017a), among other features. In what follows, we highlight only the most important of these ingredients, while we also refer readers to Pecin (2014), Pecin et al. (2017b), and Sadykov et al. (2021) for additional expositions.
We first replace the binarity constraints (10) in the set partitioning model by non-negativity constraints and obtain its LP relaxation, which is usually referred to as the master problem. The master problem has a very large number of variables, as exponentially (to number of customers) many feasible routes are typically available. Generating all of these routes to explicitly define the master problem is obviously impractical, and thus we resort to column generation. The latter leverages the idea that most of the variables will be non-basic and assuming non-zero values in the optimal solution, and hence only a subset of variables needs to be considered in practice when solving the problem. To that end, column generation aims to generate only the variables that have the potential to improve the objective function, i.e., variables with negative reduced costs. In our context, columns correspond to ng-feasible routes, and we will use these terms interchangeably. We first consider a restricted master problem (RMP) defined by a subset of ng-routes \(\tilde{R}^{ng} \subseteq R^{ng}\). After optimizing the RMP, columns with negative reduced costs will be appended to \(\tilde{R}^{ng}\) and the resulting RMP will be reoptimized. This procedure iterates until no such column exists. In that case, we say that column generation converges and the master problem has achieved optimality. If at that point the solution to the master problem is fractional, we separate and add valid inequalities, or resort to branching. The overall BPC algorithm is illustrated in Fig. 3 of the main manuscript.
1.1.1 A.1.1. Initialization
To start the algorithm, we utilize single-customer routes to build \(\tilde{R}^{ng}\), which are used to define the initial RMP. We highlight that, by constructing \(\tilde{R}^{ng}\) in this way, the initial RMP is not necessarily guaranteed to be feasible, e.g., due to the fleet size constraint (9). If that is the case, we can seek a feasible RMP via the “feasibility-recovery” step (Feillet 2010), which will be discussed in Sect. 1.
1.1.2 A.1.2. Solving pricing subproblems
After the RMP is solved, we check whether it is necessary to enlarge \(\tilde{R}^{ng}\) to include some neglected ng-feasible routes so as to improve the objective value of the RMP. This entails identifying columns with negative reduced costs, which is achieved by solving pricing subproblems. Since vehicle routes in \(R^{ng}\) can be categorized by their start depots, we consider to solve a pricing subproblem for each depot \(i \in V_d\). Without loss of generality, let node \(n+1\) correspond to the depot of interest.
In the context of vehicle routing, the pricing subproblem can be modeled as a shortest path problem with resource constraints (SPPRC) (Pugliese and Guerriero 2013). The SPPRC can be defined on a directed graph \(\overline{G} = (\overline{V}, \bar{A})\), where \(\overline{G}\) is obtained by inserting into G two copies of the chosen depot, 0 and \(n+m+1\), to represent a virtual start depot and a virtual destination depot, respectively, and by adding edges \((0, n+1)\) and \((i, n+m+1)\) for \(i \in V_c\). Clearly, in such a configuration, a feasible route always starts from node 0 and ends at \(n+m+1\), the chosen depot node \(n+1\) being the immediate node after the starting node, and all depot nodes \(i \in V_d\) used as intermediate replenishment facilities. Associated with each arc \((i, j) \in \bar{A}\) are the cost \(\bar{c}_{ij}\), travel time \(t_{ij}\) and demand \(q_j\). Note that \(q_j = 0\), if node j corresponds to a depot. The cost \(\bar{c}_{ij}\) is obtained by properly modifying \(c_{ij}\) in order to account for the contribution from current dual values to constraints (8) and (9). We associate each node \(i \in \overline{V}\) with the load limit Q and the route duration limit T. While arc \((i, j) \in \bar{A}\) is traversed by a path, denoted by P, time resource \(t_{ij}\) and capacity resource \(q_j\) are consumed. A resource’s accumulated consumption until a node visited along a path should not exceed its limit. We highlight that, if node j represents some intermediate depot facility, then the load of path P is reset to 0 to effectuate the replenishment process. The goal is to determine the minimum-cost path among all paths that start from the node 0 and end at the node \(n+m+1\), such that all resource constraints are respected.
Exact pricing: It is well-known that the SPPRC is \(\mathcal{N}\mathcal{P}\)-hard (Dror 1994). The most successful solution approach is a dynamic programming method called the labeling algorithm, which has a pseudo-polynomial time complexity (Pugliese and Guerriero 2013). The labeling algorithm works as follows. We associate an ng-feasible partial path P with a label, \(L(P) = \left( \bar{c}(P), v(P), d(P), t(P), \Pi (P), pred(P)\right) \), which stores the reduced cost, end node, load, duration, a set of forbidden nodes, and a pointer to its predecessor label. For a given pair \((i, t^\prime )\) with \(i \in \overline{V}\) and integer \(t^\prime \) such that \(0 \le t^\prime \le T\), we define a bucket \(B(i, t^\prime )\). A label L(P) is stored in bucket \(B(v(P), \lfloor t(P)\rfloor )\), where \(\lfloor \cdot \rfloor \) denotes the floor function. We remark that our proposed labeling algorithm can handle double-precision entries of the travel time matrix \(t_{ij}\).
The labeling algorithm is initialized by storing a label \(\left( 0, 0, 0, 0, \emptyset , null \right) \) in bucket B(0, 0). From bucket B(0, 0), we use dynamic programming to fill other buckets, starting with lower values of \(t^\prime \). For each integer \(t^\prime \) with \(0 \le t^\prime \le T\), the algorithm goes through \(i \in \overline{V}\) and, for each neighbor j such that \((i, j) \in \bar{A}\), evaluates the extension of the walk represented by \(B(i, t^\prime )\) to j. Given a label L(P) from bucket \(B(i, t^\prime )\), we now attempt to extend it to node \(j \in \overline{V} \setminus \Pi (P)\) with \((i, j) \in \bar{A}\). We first check whether this is a feasible extension, i.e., whether the resource consumption constraints are respected at node j. If that is the case, we obtain a new ng-feasible label and store it in bucket \(B(j, \lfloor t(P) + t_{v(P)j}\rfloor )\). As we have discussed above, the load will be reset to 0, if node j is a depot.
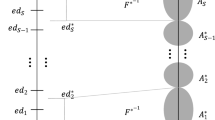
The set of forbidden nodes should be updated in a similar way as in Baldacci et al. (2011), but with some modifications due to the existence of intermediate depot nodes. In our implementation, we associate each customer node \(j \in V_c\) with an ng-set NG(j) composed of 8 nearest customer neighbors. Note that depot nodes are not included in the ng-sets of customers. When extending a label L(P) to a node \(j \in \overline{V} \setminus \Pi (P)\), its successor’s forbidden set is updated to be \((\Pi (P) \cap NG(j)) \cup \{j\}\), if node j is a customer; otherwise, the successor maintains the same forbidden set as the label itself. The idea behind this is that enforcing forbidden sets and thus ng-routes is to seek for partial elementarity of routes generated in the SPPRC. Since the elementarity of a given route is not affected by the existence of depot nodes, those nodes should be excluded from forbidden sets. Figure 9 illustrates our modifications for extending paths.
When no more label extensions can be made, we collect all columns stored in buckets \(B(n+m+1, t^\prime )\) with \(0 < t^\prime \le T\) and return all those with negative reduced costs.
To accelerate the labeling algorithm, it is crucial to check for dominance relationships so as to avoid some unnecessary label extensions. More specifically, before storing a new ng-feasible label, we first check whether it dominates or is dominated by existing labels stored in buckets. We say that a label \(L(P_1)\) dominates another label \(L(P_2)\) if, for any feasible path extended from \(P_2\), we can always find a feasible path extension from \(P_1\) and this extended path is not more costly. Sufficient conditions for this are given by (11)–(15).
We highlight that conditions (11)–(15) are indeed sufficient because the total load delivered by a vehicle along the route always increases, and is only reset to 0 when a depot node is visited. A newly generated label L(P) is saved only if it is not dominated, and existing labels that are dominated by L(P) will be removed. In our implementation, the dominance rule is only tested between a label L(P) and labels stored in buckets \(B(v(P), t^\prime )\) with \(\max \{0, \lfloor t(P)\rfloor - 10\} \le t^\prime \le \lfloor t(P)\rfloor \).
We solve a pricing subproblem for each depot \(i \in V_d\) and append into \(\tilde{R}^{ng}\) the up to 20 columns with the most negative reduced costs. Let \(\bar{c}_{min}\) denote the minimum cost among the returned columns. Clearly, \(\bar{c}_{min}\) is the minimum reduced cost of all ng-feasible routes.
Variable fixing: Let \(z^*\) denote the current RMP optimal value. It is well-known that one can obtain a valid lower bound, \(z^{LB} := z^* + \text {min} \{K, |V_c|\} \bar{c}_{min}\), also known as the Lagrangian bound (Lübbecke and Desrosiers 2005). We emphasize that the fleet size bound K is updated, whenever branching on the fleet size is executed (see later for details on branching rules). In addition to pruning branch-and-bound nodes, the Lagrangian bound may also be used for variable fixing.
Let us define the primal-dual gap, \(z^{gap} := UB - z^{LB}\). One can easily show that a column with a reduced cost larger than \(z^{gap} + \bar{c}_{min}\) will not be part of any feasible solution better than the incumbent (Sadykov et al. 2021); thus, such columns can be excluded from consideration. In our implementation, we employ a technique called arc fixing (Irnich et al. 2010). Specifically, given arc \((i, j) \in \bar{A}\), if every feasible column traversing this arc has a reduced cost larger than \(z^{gap} + \bar{c}_{min}\), then this arc can be omitted from consideration. To reach such a conclusion and omit an arc, we need to apply the labeling algorithm we discussed above in a backward fashion. The backward labeling algorithm works in a similar way as the regular (forward) labeling, but with the following minor modifications: (1) it is initialized by storing the first label \(\{0, n+m+1, Q, T, \emptyset , null\}\) and starts with higher values of \(t^\prime \) for label extension; (2) when extending label L(P) to some node j, the new label’s duration is set to \(t(P) - t_{jv(P)}\); (3) when extending label L(P) to some node j, the new label’s load is set to \(d(P) - q_{v(P)}\), unless j represents some intermediate depot facility, in which case it is set to Q; (4) the inequality conditions (13) and (14) in the dominance check are reversed; (5) the dominance relationship is tested between a label L(P) and labels stored in buckets \(B(v(P), t^\prime )\) with \(\lfloor t(P)\rfloor \le t^\prime \le \min \{\lfloor t(P)\rfloor + 10, T\}\); (6) columns stored in buckets \(B(0, t^\prime )\), such that \(0 \le t^\prime < T\), are returned if they are associated with negative reduced costs.
We separately perform a full run of both forward and backward labeling. The minimum reduced cost of a column passing by an arc \((i, j) \in \bar{A}\), denoted by \(\bar{C}_{ij}\), can be obtained by concatenating the labels in \(B(i, t^\prime )\) from the forward run with the labels in \(B(j, t^{\prime \prime })\) from the backward run for integers \(t^{\prime }\) and \(t^{\prime \prime }\) such that \(0 \le t^\prime \le T\) and \(t^\prime + \lfloor t_{ij}\rfloor \le t^{\prime \prime } \le T\). In particular, the concatenation between a label \(L(P^{\mathcal {F}})\) in \(B(i, t^\prime )\) from the forward run and a label \(L(P^{\mathcal {B}})\) in \(B(j, t^{\prime \prime })\) from the backward run is feasible, if conditions (16)–(18) are satisfied.
This produces a feasible column with the reduced cost of \(\bar{c}\left( P^{\mathcal {F}}\right) + \bar{c}_{ij} + \bar{c}\left( P^{\mathcal {B}}\right) \). Then \(\bar{C}_{ij}\) is the minimum reduced cost for generated columns from feasible concatenation along arc (i, j). If \(\bar{C}_{ij}\) is larger than \(z^{gap} + \bar{c}_{min}\), then one can eliminate the arc (i, j) from \(\bar{A}\). Since arc fixing is typically effective when \(z^{gap}\) becomes small, we begin to fix arcs by reduced costs after the initial convergence of column generation and when \(z^{gap}/UB\) is below \(5\%\). In our implementation, arc fixing is performed only if \(z^{gap}\) decreases by at least \(10\%\) since the last call.
Route enumeration: As Baldacci et al. (2008) suggested, one can enumerate all elementary columns with reduced costs less than \(z^{gap} + \bar{c}_{min}\), since only these columns may contribute to a solution better than the incumbent. We adopt the idea from the work of Contardo and Martinelli (2014) and attempt to enumerate all possible routes when the primal-dual gap becomes small. In particular, after each call of variable fixing, if the primal-dual gap is below \(1\%\), we then attempt to enumerate all columns that have the potential to improve the objective function. In order to enumerate elementary routes using the forward labeling algorithm we discussed above, NG(i) is defined to be the customer set \(V_c\). As a result, \(\Pi (P)\) is simply the set of visited customer nodes along path P. Furthermore, as suggested by Pecin et al. (2017b), the dominance rule should be updated in the following way. First, the condition (15) is modified to \(\Pi (P_1) = \Pi (P_2)\). Second, we define for each label L(P) an extra member c(P) to indicate the original accumulated travel cost along path P, and then, the condition (11) is revised to be \(c(P_1) \le c(P_2)\). The route enumeration procedure can be accelerated by using the so-called completion bound (Contardo and Martinelli 2014), which can be computed for free from the variable fixing step. For the sake of brevity, we refer readers to Pecin (2014) and Pecin et al. (2017b) for details.
In our implementation, the enumeration procedure is interrupted when the number of labels exceeds \(1.0 \times 10^6\), or when the number of enumerated routes exceeds \(1.0 \times 10^5\). After a successful enumeration, generated columns are not immediately appended to \(\tilde{R}^{ng}\) but saved in a pool. At this point, one can also erase non-elementary columns from \(\tilde{R}^{ng}\). Finally, once the total number of columns from \(\tilde{R}^{ng}\) and the pool is less than \(1.0 \times 10^4\), we append integrality constraints (10) to the RMP and solve the resulting integer program. Otherwise, in the upcoming iterations, we can simply inspect columns saved in the pool and return at most 150 of them with negative reduced costs.
Heuristic pricing: The column generation procedure can be further accelerated by using a fast heuristic pricing methods called “bucket pruning”, which was introduced in Fukasawa et al. (2006). Simply put, this method relaxes the dominance check by only considering the condition (11). The trade-off to this efficiency is that non-dominated labels may be dropped, though it is expected that those would be less likely to lead to optimal solutions. In our implementation, we opted to first apply the heuristic labeling algorithm to generate columns with negative reduced costs, and to resort to the exact algorithm only if the heuristic method fails to identify any column. In particular, in each iteration, we return the up to 30 columns with the most negative reduced costs from heuristic pricing.
1.1.3 A.1.3. Cutting planes
Once the column generation has converged, the master problem has achieved its optimality. At this point, if the current LP optimal solution is not integral, we try to identify strengthening inequalities to exclude the fractional solution from the relaxed feasible space. For this, we consider two types of valid inequalities, namely Rounded Capacity Inequalities (RCI) (Laporte and Nobert 1983) and Subset Row Cuts (SRC) (Jepsen et al. 2008).
The separation routine for RCI is synopsized as follows. Let \(G^* = (V, A)\) be a support graph corresponding to the current solution to an RMP. We first shrink the set of depot nodes, \(V_d\), to be a single node, which results in a support graph for the classic capacitated vehicle routing problem. We then apply a tabu search algorithm inspired from Augerat et al. (1998) to identify violated RCI. In the context of a branch-price-and-cut algorithm, RCI are so called “robust” cuts (de Aragao and Uchoa 2003) because their corresponding dual values can be properly accommodated into the modified arc cost in the SPPRC; thus, adding RCI into the set partitioning model as strengthening inequalities will not complicate the solution of pricing subproblems.
With regards to SRC, it is well-known that they usually help to close the primal-dual gap significantly; however, these are known to be “non-robust” cuts, since their dual values cannot be easily combined into the arc cost in the SPPRC, changing the pricing subproblem structure. In essence, each additional SRC makes pricing harder. To mitigate the negative effect of SRC on solving SPPRC subproblems, we adopt a variant of SRC, called limited-arc-memory subset row cuts (lm-SRC), which was proposed in Pecin et al. (2017a). The lm-SRC are still non-robust cuts but have much less impact on solving pricing problems (Pecin et al. 2017b). We use the procedure proposed in Pecin et al. (2017c) to separate lm-SRC. In particular, for every \(i \in V_c\), we define \(N(i) \subseteq V_c\) as the set containing the 15 other customers closest to i and then test the violation of all SRC obtained by applying multipliers to all base sets S with cardinalities 3, 4 and 5, and for each i and j in S, \(j \in N(i)\). After violated SRC are identified, we add their corresponding limited-arc-memory version. To accommodate the use of lm-SRC, the labeling algorithm is modified in the following aspects: (1) we define a state for each active cut; (2) the contributions from dual values to lm-SRC are taken into consideration when computing the reduced cost for a new label; (3) the condition (11) in the dominance check is updated to account for the dual values to lm-SRC. Readers are referred to Pecin et al. (2017c) and Sadykov et al. (2021) for further details on lm-SRC separation.
We now discuss our overall cut separation protocol. At the root node, we first attempt to identify violated RCI and resort to lm-SRC only if no RCI is found or if “tailing-off” is detected for RCI. We define tailing-off when the node primal-dual gap \(z^{gap}\) has not improved by at least \(0.1\%\) during the past 3 iterations. In all other nodes of the branch-and-bound tree, both RCI and lm-SRC are separated in every round. If the tailing-off condition is satisfied, we stop the cut separation and perform branching. Since, as discussed, the lm-SRC have a negative effect on our ability to keep solving SPPRC subproblems, we add into the set partitioning model only the 5 most violated lm-SRCs per round and add at most 300 lm-SRCs in total. We also remove non-active lm-SRC from the model before each cut separation round. After route enumeration at a given node is completed, all lm-SRC are lifted to their SRC counterparts, since we no longer need to solve the SPPRC.
1.1.4 A.1.4. Branching strategy
When the optimal solution to the master problem is not integral and no violated cuts can be identified, or if we have decided to stop adding cuts due to tailing-off, we then proceed to branching. More specifically, we first attempt to branch on the number of used vehicles, since computational experience suggests this can have a more profound impact on the branch-and-bound node’s lower bound; if this is not applicable, then we perform branching on edges by choosing the edge with value closest to 0.5, as determined by adding up all fractional values of routing variables of those routes that involve the edge. Readers are referred to Feillet (2010) and Røpke (2012) for details. We emphasize that the branching rules we adopt do not change the pricing structure and, thus, do not increase the complexity of solving the SPPRC subproblems.
1.1.5 A.1.5. Other implementation details
Feasibility-recovery: When the RMP becomes infeasible (e.g., due to branching or because the initial RMP itself is infeasible), we resort to the feasibility-recovery step as suggested by Feillet (2010), which corresponds to the “Phase I” step in the classic simplex algorithm. In particular, we introduce a dummy variable into the RMP with its coefficient at each constraint being the right-hand side and its objective coefficient being \(UB + \epsilon \), where \(\epsilon > 0\) (we used \(\epsilon = 0.1\)). Clearly, the modified linear program becomes feasible. The resulting linear program is then solved and its dual values are used to generate new columns with negative reduced costs so as to recover the RMP feasibility. When column generation converges, i.e., the LP optimality is achieved, and assuming the dummy variable attains a value of zero, the primal feasibility of the RMP is recovered; otherwise, if the dummy variable attains a non-zero value, the LP optimal value must be \(UB + \epsilon \) (due to complementary slackness), resulting in the node being pruned by bound in the branch-and-bound tree.
Primal heuristics: Whenever the RMP is solved, we apply a simple rounding heuristic in an attempt to find better feasible solutions than the incumbent. In our implementation, elementary columns with their current corresponding LP optimal values above 0.5 are collected and we check whether the routing plan composed of these columns is feasible. If this leads to a feasible solution with an objective value better than the incumbent, we then update the upper bound UB.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, A., Arbogast, J.E., Bonnier, G. et al. Estimating the marginal cost to deliver to individual customers. Optim Eng 24, 2409–2447 (2023). https://doi.org/10.1007/s11081-022-09779-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-022-09779-4