1 Introduction

With airlines, Air Navigation Service Providers (ANSPs), and the International Civil Aviation Organisation (ICAO) all keen to reduce the environmental impact of commercial flight (ICAO 2020; Molloy 2020; AirlinesUK 2019), it has been shown that Trajectory Based Operations (TBO) provide the key to improving overall efficiency (Wickramasinghe et al. 2012; García-Heras et al. 2014). This approach focuses on designing individual flight routes accounting for weather conditions in order to optimize efficiency with regard to a number of different factors. For long haul flights, such as those between London Heathrow Airport (LHR) and John F. Kennedy Airport in New York (JFK), for which the cruise phase makes up around 92% of the ground distance of the flight (as shown in Wells et al. 2021), TBO promises the greatest rewards (Girardet et al. 2014).

Time optimal routing has been shown to reduce fuel burn when altitude and airspeed are fixed, compared to the tracks provided across the North Atlantic by NATS and NAV CANADA (Wells et al. 2021). However, this option is not necessarily the most practical for airlines and airports. For operational and financial reasons airlines also need to adhere to their published timetables. Flights arriving early create additional costs, through extra fuel burned in holding patterns, missed connecting flights, blocked gates and additional crew time. Customer dissatisfaction is also a key issue for airlines when delays occur. If flight trajectories are planned to ensure a fixed flight time, whilst minimising fuel burn, then the additional costs to both the airlines and the environment associated with early arrival can be saved.

Optimal control theory (Kirk 1970; Macki and Strauss 1982; Bressan and Piccoli 2007) is applied here to formulate a problem leading to fixed time fuel minimal trajectories subject to arrival constraints, an aerodynamic fuel-burn model and a data-driven wind field. The fuel usage of trajectories generated by two finite horizon optimal control formulations are compared. In the first, a single control variable is given as a set of position-dependent aircraft headings. The second formulation varies both the headings and the airspeed of the aircraft. Fuel consumption is modelled with a new physics-driven fuel burn function, which is aircraft type specific (Poll and Schumann 2021a, b). Optimal trajectories are found numerically using a reduced gradient approach.

Long range cruise trajectories minimising fuel for a fixed mass aircraft have previously been researched by others using control variables of thrust and flight path angle (Schultz and Zagalsky 1972; Speyer 1973) or lift and thrust (Schultz 1974; Menon 1989), but these have not accounted for the wind field. In these papers the fuel flow is minimised for a set distance of flight. Wind has been factored into fixed range cruise calculations which compare fixed and free thrust as airspeed varies (Erzberger and Lee 1980), but here a direct operating cost is minimised, with this cost dependent on both time of flight and fuel use. Similar comprehensive research into trajectory optimisation for hybrid UAVs, incorporating weather data and optimising for energy has been completed recently, but these routes are time variable (Dobrokhodov et al. 2020).

Fixed time trajectories minimising direct operating cost have also been designed, but unlike the current research, the optimal control model is set up with a free final time (Sorensen and Waters 1981; Burrows 1983). The trajectory best fitting the imposed arrival time constraint is then selected. Other methods have been used to solve a minimum fuel cruise at constant altitude with fixed arrival time (García-Heras et al. 2014; Franco and Rivas 2011), but these either did not consider the effect of wind at all or simplified the wind fields. Optimal routes through realistic wind fields are often very different from their wind-free equivalents (Girardet et al. 2014).

The minimum fuel optimisation problem for a fixed time journey has, therefore, been examined previously. The novelty in the approach shown here lies in:

  • Applying a recently developed, novel, analytic aerodynamic fuel-burn model (Poll and Schumann 2021a, b) that is quicker and easier to use in complex computation schemes than the standard EUROCONTROL Base of Aircraft Data (García-Heras et al. 2014; Wickramasinghe et al. 2012; Soler et al. 2020; Yamashita et al. 2021; Matthes et al. 2021; Yamashita et al. 2020). This new method is open source and fully transparent.

  • A numerical assessment across 91 days, covering the entire winter period from 1st December, 2019 to 29th February, 2020, using real atmospheric data.

This paper is set out in five sections. In Sect. 2, the system dynamics, a description of the optimal control formulation and an outline of the approximate synthesis of optimal trajectories are discussed. Section 3 contains model data specific to the the data-driven wind field and the fuel burn function. In Sect. 4 fuel savings by incorporating both heading angle and airspeed control, rather than just heading angle, are quantified and the effect of differing wind fields on results is analysed. Finally, the results are summarised and discussed in Sect. 5.

2 Mathematical modelling for trajectory planning

In this section the dynamical system governing the trajectory of an aircraft is presented. An optimal control formulation is stated to minimize fuel burn along a fixed time horizon with a fixed departure point. The destination target comprises all points within \(1~ {\hbox {km}}\) of the point \((\lambda _{dest},\phi _{dest})\). Two different optimal control formulations are presented, representing fixed and variable airspeed models.

We then redefine this continuous system as a set of discrete paths, making a piecewise continuous route, in order to render the solution more practical in an operational sense. The numerical method applied to provide an approximate solution to this discrete problem is then discussed. The nomenclature for variables used throughout the paper is defined in Table 1.

Table 1 Nomenclature
Full size table

2.1 System dynamics for the trajectory of an aircraft

A simplified model for the trajectory of an aircraft is considered. The model is a variation of Zermelo’s navigation problem transformed conformally onto a sphere, but here the objective is to minimise fuel burn rather than flight time (Zermelo 1930). The aircraft travels the surface of a spherical shell with the same radius as the Earth. Although the aircraft will actually travel at a fixed altitude h above this shell, as \(h \ll R\) this can be approximated by R in line with previous research (Arrow 1949; Jardin and Bryson 2012; Ng et al. 2014; Kim et al. 2016; Williams 2016). The aircraft trajectory, is characterised by longitude, \(\lambda\), latitude, \(\phi\), and mass, M, at any time t. The rate of change of these states depends both on airspeed and wind speed. The aircraft is controlled through its heading angle, \(\psi\), and its airspeed, V. By varying these quantities, the path of the aircraft will be altered, thus resulting in different regions of winds being encountered. The airspeed V will determine which winds it is possible to access within the given fixed time of flight. This initial continuous problem assumes that:

  1. 1.

    The aircraft’s heading angle and airspeed are varied continuously.

  2. 2.

    Airspeed will remain within operational bounds throughout the flight.

The equations of motion for the controlled aircraft are given by:

$$\begin{aligned} {\dot{\lambda }}&=\frac{1}{R\cos {\phi (t)}}(V(t)\cos \psi (t) +u(\lambda (t),\phi (t))) \end{aligned}$$
(1)
$$\begin{aligned} {\dot{\phi }}&=\frac{1}{R}(V(t)\sin \psi (t) +v(\lambda (t),\phi (t))) \end{aligned}$$
(2)
$$\begin{aligned} {\dot{M}}&=-g(\lambda (t),\phi (t),M(t),V(t)) \end{aligned}$$
(3)

Equation (1) is derived from the zonal components of both airspeed and wind speed, mapped conformally onto a sphere. Equation (2) is the sum of the meridional components of airspeed and wind speed, again multiplied by the correct transformation factor to allow for all \((\lambda ,\phi )\) co-ordinate pairs to lie on a spherical shell. Equation (3) is the rate of decrease of fuel over time, according to fuel burn rate function g which is discussed in detail in Sect. 3.2. However, in order to avoid scaling issues, as the state variables are of very different orders, it is necessary to non-dimensionalise this dynamical system. Of the state variables, only M, the mass of the aircraft has a dimension, as angle measures are considered dimensionless. In the same way airspeed, V, time, t, fuel burn rate, g, zonal wind speed, u and meridional wind speed, v must be similarly scaled. The following definitions will be used:

$$\begin{aligned} M^{*}&=\frac{M}{M_{ref}} \end{aligned}$$
(4)
$$\begin{aligned} V^{*}&=\frac{V}{V_{ref}}\end{aligned}$$
(5)
$$\begin{aligned} t^{*}&=\frac{V_{ref}t}{R}\end{aligned}$$
(6)
$$\begin{aligned} g^{*}&=\frac{Rg}{M_{ref}V_{ref}}\end{aligned}$$
(7)
$$\begin{aligned} u^{*}&=\frac{u}{V_{ref}}\end{aligned}$$
(8)
$$\begin{aligned} v^{*}&=\frac{v}{V_{ref}} \end{aligned}$$
(9)

leading to the non-dimensionalised dynamical system of:

$$\begin{aligned} \frac{\partial \lambda }{\partial t^{*}}&=\frac{1}{\cos {\phi (t^{*})}}(V^{*}(t^{*})\cos \psi (t^{*}) +u^{*}(\lambda (t^{*}),\phi (t^{*})))\end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial \phi }{\partial t^{*}}&=V^{*}(t^{*})\sin \psi (t^{*}) +v^{*}(\lambda (t^{*}),\phi (t^{*}))\end{aligned}$$
(11)
$$\begin{aligned} \frac{\partial M^{*}}{\partial t^{*}}&=-g^{*}(\lambda (t^{*}),\phi (t^{*}),M^{*}(t^{*}),V^{*}(t^{*})) \end{aligned}$$
(12)

This describes a continuous problem, but operationally the trajectory is viewed as a piecewise continuous route. It comprises rhumb-line tracks, the paths with constant heading angle around the globe between two given points, between waypoints corresponding to the start and end of equal time intervals. We now discuss this discrete optimal control formulation and its approximate synthesis.

2.2 Optimal control formulation and approximate synthesis

The objective of the dynamic optimization procedure is to compute the airspeeds and headings that will ensure fuel burn across the trajectory is minimized. At first, the control variables are not constrained. However, it is assumed that airspeed, where this is allowed to vary, will lie within a specified operational range.

In formulating the optimal control problem a constant altitude flight is considered, starting from the initial position, \((\lambda _{dept},\phi _{dept})\) at a time \(t=0\) to a final target that encompasses all points within a certain distance, \(\delta _{dest}\), of \((\lambda _{dest},\phi _{dest})\) at a final time of \(t=t_{f}\), with a fixed time of flight.

An aircraft arriving within \(\delta _{dest}=1000~{\text {m}}\) of the destination airport is assumed to have completed its journey successfully. This terminal constraint is based on the Haversine formula (Veness 2019):

$$\begin{aligned} a&= \sin ^{2}(|\phi _{dest}-\phi (t_{f})|/2) + \cos (\phi _{dest})\cos (\phi (t_{f}))\sin ^{2}(|\lambda _{dest}-\lambda (t_{f})|/2)\nonumber \\ d&=2R{\text {atan2}} (\sqrt{a}, \sqrt{1-a}) \end{aligned}$$
(13)

where atan2 is the four-quadrant inverse tangent of the two real values in the function bracket, d is the spherical distance to the destination airport in metres and R is the radius of the Earth.

The mass, M(t) is not constrained, but is assumed to lie between the start of cruise mass (taken to be 97.5% of the take-off mass and denoted here as SOCM) and the operational empty mass, (OEM). At \(t=0\), \(M(0)=M_{dept}\) which is the SOCM. For a Boeing 777-236ER aircraft, this is calculated as 221 826 kg flying East and 235 112 kg flying West, using the method developed in Poll and Schumann (2021b).

The formulation involving two control variables is referred to subsequently as OCP2. The first control is the heading angle in radians, measured anti-clockwise from due East, in line with the original derivation of the dynamical system in Zermelo (1930). The true airspeed, V(t), is the second control and is assumed to stay within the operational boundaries of 199 to 252 \({{\text {m s}}^{-1}}\). (This corresponds to a Mach number range of 0.58 to 0.73.) A second formulation, referred to as OCP1, is a simplified version of OCP2, involving just a single control variable, the heading angle \(\psi (t)\). In both cases, as flights progress, at each time step mass will be reduced by the amount of fuel burned during the preceding time interval.

In the continuous problem with two control variables, outlined in Sect. 2.1, the optimal heading angle \(\psi (t)\) and airspeed V(t) are found by minimising the cost functional:

$$\begin{aligned} J^{*}=\underset{\psi (\cdot ),V(\cdot )}{\min }\int \limits _{0}^{t_{f}}g(\lambda (t),\phi (t),M(t),V(t)) \,dt\,, \end{aligned}$$
(14)

where \(g(\lambda ,\phi ,M,V)\) is the physics-driven fuel burn function discussed further in Sect. 3.2, and subject to Eqs. (1)–(3).

In the case of OCP1, where a single variable only is applied, the system dynamics remain as described in Eqs. (1)–(3), but taking a constant airspeed, i.e. \(V(t)=V\). The cost functional now becomes:

$$\begin{aligned} J^{*}=\underset{\psi (\cdot )}{\min }\int \limits _{0}^{t_{f}}g(\lambda (t),\phi (t),M(t),V) \,dt\ \end{aligned}$$
(15)

However, for operational applicability, we do not wish to solve this continuous problem, but the corresponding discrete problem.

The construction of a nonlinear optimization approach continues with the discretization in time of the system dynamics. A uniform temporal grid with N time steps of size \(\varDelta t\) is set. The spatial states at the start and end of each time interval are considered as waypoints in the flight and the temperature and wind conditions at each of these \(N+1\) waypoints are used in updating the dynamical system as the trajectory progresses. The third state, the mass of the aircraft at the start of each time interval is used in evaluating the fuel burn across each time interval. This is done using a Runge-Kutta 4th order method with fixed time step for Eqs. (1)–(3), providing a set of discrete state variables \(\{\lambda (i\varDelta t^{*}),\phi (i\varDelta t^{*}),M(i\varDelta t^{*})\}_{i=0}^{N}\), which we denote by \((\lambda (i),\phi (i),M(i))\). This leads to the following nonlinear optimization problem for the non-dimensionalised system:

$$\begin{aligned}&J^*_{\varDelta t^{*}}=\underset{\lambda (\cdot ),\phi (\cdot ),M^{*}(\cdot )\in {\mathbb {R}}^N}{\min }\varDelta t^{*}\sum _{i=1}^N g^{*}\big (\lambda (i),\phi (i),M^{*}(i),V^{*}(i)\big )\,, \end{aligned}$$
(16)
$$\begin{aligned}&\text {subject to:}\nonumber \\&\lambda (i+1)=\lambda (i)+\varDelta t^{*}\varPhi _{\lambda }(\lambda (i),\phi (i),M^{*}(i),\psi (i),V^{*}(i),\varDelta t^{*})\,,\end{aligned}$$
(17)
$$\begin{aligned}&\phi (i+1)=\phi (i)+\varDelta t^{*}\varPhi _{\phi }(\lambda (i),\phi (i),M^{*}(i),\psi (i),V^{*}(i),\varDelta t^{*})\,,\end{aligned}$$
(18)
$$\begin{aligned}&M^{*}(i+1)=M^{*}(i)+\varDelta t^{*}\varPhi _{M^{*}}(\lambda (i),\phi (i),M^{*}(i),\psi (i),V^{*}(i),\varDelta t^{*})\,,\nonumber \\&i=0\ldots N\,,\end{aligned}$$
(19)
$$\begin{aligned}&(\lambda (0),\phi (0),M^{*}(0))=\left( \lambda _{dept},\phi _{dept},\frac{M_{dept}}{M_{ref}}\right) \,,\end{aligned}$$
(20)
$$\begin{aligned}&d\le \delta _{dest}\,,\end{aligned}$$
(21)
$$\begin{aligned}&M^{*}(i)\in \left[ \frac{\text {OEM}}{M_{ref}},\frac{\text {SOCM}}{M_{ref}}\right] \,\end{aligned}$$
(22)
$$\begin{aligned}&V^{*}(i)\in \left[ \frac{V_{min}}{V_{ref}},\frac{V_{max}}{V_{ref}}\right] \,. \end{aligned}$$
(23)

The function \(\varPhi\) denotes an explicit RK4 time integration expressed as a single-stage update. Controls are considered as piecewise constant, as across each 100 s time step controls and atmospheric conditions are taken to be constant. This is a justifiable assumption, as a 100 s time step is small in comparison to the whole journey of about six hours flying East and eight hours flying West. The last two equations of this program include operational constraints on the aircraft mass and airspeed.

There are different numerical optimization solvers which can deal with the solution of the nonlinear programming problem (16)–(23). We chose not to use a specialised commercial solver here, but rather one widely used throughout the scientific community to allow for easier replication of results, with the data, formulae and processes all in the public domain. In this paper Matlab’s fmincon solver was used within the multistart solver from Matlab’s Global Optimization Toolbox (Waltz et al. 2006; Byrd et al. 1999, 2000; Ugray et al. 2007). The multistart solver generates a specified number of starting points randomly within the bounds of the given problem structure. It then filters to feasible points before running these through the fmincon function, as a local solver. Once all points have been run, the local solver output with the lowest cost is found. Fmincon uses an interior point algorithm to alter heading angles and airspeeds at each iteration to ensure that the cost function is reduced. This continues until either the step tolerance or the optimality tolerance fall below given bounds. Step tolerance is a relative bound which compares the size of a control value to the size of the previous one. Optimality tolerance is a measure of how the objective function is varying in all feasible directions. Its value is taken as the infinity norm of the sum of the partial derivatives of \(J^{*}\) with respect to the control variables at each timestep \(i=1,2,\ldots N\):

$$\begin{aligned} \sum _{i=1}^{i=N}\frac{\partial J^{*}}{\partial {\psi (i)}}+\sum _{i=1}^{i=N}\frac{\partial J^{*}}{\partial V^{*}(i)} \end{aligned}$$
(24)

However, gradients of \(J^{*}\) are computed using finite differences, avoiding an explicit numerical calculation of gradients for the wind field and the fuel burn model. This is a standard procedure, as encountering objective functions where the evaluation of derivatives is not practical is not unusual in real-world systems (Colson and Toint 2001; Naresh Kumar et al. 2018). As fmincon finds local minima of a problem, there is no guarantee that results will be globally optimal, but by using fmincon within the multistart solver the method becomes more robust.

3 Weather data and fuel burn modelling

In order to solve the discrete problem described in Eqs. 16–23, data regarding zonal (eastward) and meridional (northward) winds and temperatures from daily averaged re-analysis data is needed, in addition to a model for the aerodynamic fuel burn function. These are detailed fully in this section.

3.1 Data-driven wind and temperature fields

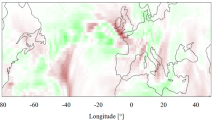
The use of realistic atmospheric data in these simulations is critical in ensuring their relevance to improving trajectory-based operations. Plots of two sample wind fields are shown in Fig. 1.

Fig. 1
figure 1

Contour plots showing strength of winds in \({{\text {m s}}^{-1}}\) across the North Atlantic on 1st December, 2019 and 9th February, 2020. Behind these contour plots is a quiver plot of the same winds to show the direction of flow. These two wind fields are representative of the winter period. The positions of LHR and JFK are represented by red stars

Full size image

Determination of fuel burn rate used in Eq. (3) is dependent on temperature at any point along a trajectory, the mass of the aircraft and also on the airspeed of the aircraft. The temperature is required in the calculation of both the Mach number and the dynamic viscosity of the air, both of which values are used to find the current fuel efficiency of the aircraft at any point on a trajectory. Numerical solution of Eqs. (1)–(2), necessitates obtaining speeds for the zonal and meridional winds at any point across the North Atlantic. Thus both records of wind speed and temperature are needed in order to find admissible trajectories. Contour plots of the two temperature fields corresponding to the wind fields in Fig. 1 are shown in Fig. 2.

Fig. 2
figure 2

Contour plots showing temperature variation in degrees K across the North Atlantic on 1st December, 2019 and 9th February, 2020. These two temperature fields correspond to the wind fields shown in Fig. 1. The positions of LHR and JFK are represented by red stars

Full size image

In this research all atmospheric data has been downloaded from the re-analysis data set provided by the National Center for Atmospheric Research (Kalnay et al. 1996). This comprises an atmospheric model and a large array of observations combined via data assimilation to produce a weather hindcast. Wind velocity and temperature values are given for a global grid of resolution 2.5\(^{\circ }\) as daily averages. Linear interpolation is then applied to obtain wind components and temperature at specific points in a trajectory. This approach is justified as long haul flight routes have been shown to be largely insensitive to the resolution of weather data (Lunnon and Mirza 2007) and the evolution of the jet stream at this altitude shows little variation across a 24-hour period (Mangini et al. 2018). The use of daily wind data is in line with methods used in previous transatlantic trajectory research (Wells et al. 2021; Kim et al. 2020; Williams 2016; Mangini et al. 2018).

Wind fields can be considered to be smooth, as there are no flow discontinuities in the atmosphere. Molecular viscosity prevents discontinuities from occurring by smoothing them out over the Kolmogorov scale (which is typically a few millimeters). There are no flow fluctuations smaller than this scale.

3.2 Fuel burn model

In the vast majority of research relating fuel burn to aircraft trajectories, EUROCONTROL’s Base of Aircraft Data Version 4 (BADA) method is used to model aircraft fuel flow (EUROCONTROL 2021). This is true for recent papers looking for climate optimized trajectories (Matthes et al. 2020, 2021; Yamashita et al. 2020, 2021) as well as previous research into fuel-optimal routing (García-Heras et al. 2014; Wickramasinghe et al. 2012; Soler et al. 2020). However, we have chosen to use a new analytic method for estimating the fuel burn rate of commercial passenger aircraft due to Poll and Schumann (2021a, b). This method is more ideally suited to our research, being quicker and easier to use than BADA as part of a complex computation scheme. As the method is open source, there is no need for a licence to access it and there are no restrictions on its use. The derivation of the method has been set out in refereed journals, ensuring that its validity has received appropriate endorsement.

The fuel burn rate (in  \({{\text {kg s}}^{-1}}\)) can be expressed as:

$$\begin{aligned} g=\frac{VW}{\left( \eta _{0}\frac{L}{D}\right) LCV} \end{aligned}$$
(25)

where W is the weight of the aircraft in N, V denotes the airspeed in  \({{\text {m s}}^{-1}}\), LCV is the lower calorific value of aircraft fuel (43 M \({{\text {J kg}}^{-1}}\) for kerosene) and \(\eta _{0}\frac{L}{D}\) is the maximum value of overall efficiency of the propulsion system, multiplied by the lift-to-drag ratio.

Obtaining the fuel burn rate for each step of a trajectory depends on aircraft specific parameters and International Standard Atmosphere parameters. Here it is assumed that a Boeing 777-236ER aircraft is used, as this is the model currently flown most frequently in transatlantic routes between London Heathrow Airport and John F. Kennedy Airport in New York (Flightradar24 2020). In addition, the fuel burn is also dependent, at each point along a trajectory, on the altitude and airspeed of the aircraft, and on the environment temperature \(T=T(\lambda ,\phi )\). The term \(\eta _{0}(L/D)=\eta _{0}(L/D)(T)\) has a nonlinear physical dependence on the temperature field, which has been modelled in Poll and Schumann (2021a, b).

The aircraft are assumed to fly along the 250 hPa isobar, which corresponds to an altitude of approximately 34 000 feet. This is close to the average cruise altitude for flights across the North Atlantic and the flight level at which the organised track system is currently calculated (Mangini et al. 2018). Aircraft on this route rarely change altitude and so this is an acceptable simplification.

The fuel burn rate can be seen in Fig. 3 for a range of airspeeds and temperatures. The airspeeds are determined by the model of aircraft flown, in this case the Boeing 777-236ER, and the temperatures are representative of those recorded across the North Atlantic during the winter period from 2019 to 2020.

Fig. 3
figure 3

Surface plot showing fuel burn rate variation with airspeed and temperature. The range of airspeeds shown are those practical for a Boeing 777-236ER flying at a cruise altitude of 34 000 ft. The temperatures cover a realistic range for the winter season over the North Atlantic

Full size image

Where both heading angle and airspeed are controlled, fuel burn rate will vary with airspeed, mass and temperature, whereas in the second case, where airspeed remains constant, fuel burn rate will vary only due to the mass of the aircraft and the temperature encountered along the route, which can be seen to be a small effect.

4 Results

In this section, the particular parameters for the numerical models used are specified and then results, given the relevant weather data, are presented and discussed.

4.1 Parameters of the system

Trajectories are modelled between LHR (51.5\(^\circ\) N, 0.5\(^\circ\) W) and JFK (40.6\(^\circ\) N, 73.8\(^\circ\) W) both eastbound and westbound. This particular route has been chosen as it is not only one of the busiest, but goes through the slowly evolving background wind field provided by the jet stream, the prevailing eastbound nature of which causes the challenges of flying in each direction to be quite different.

All flights modelled occur between 1st December, 2019 and 29th February, 2020. This allows the full range of winter weather systems to be considered (Irvine et al. 2013), as the North Atlantic Oscillation has been shown to cause transatlantic routes to vary strongly (Woollings and Blackburn 2012; Kim et al. 2016). In the future it is expected that cruise level winds in this region will increase in speed due to climate change (Irvine et al. 2016; Williams 2016; Simpson 2016; Kim et al. 2020), so their inclusion in routing calculations seems set to become increasingly important.

Further model parameters include time step length, number of time steps in each direction, search algorithm tolerances, chosen airspeeds for the initialization of the OCP2 formulation, the fixed airspeed for OCP1 and the initial estimate for the heading angle at each time step for both OCP1 and 2.

The time step length was chosen following a sensitivity analysis and a time step of \(\varDelta t=\) 100 s allows a stable and consistent application of the numerical method, whilst not unduly increasing truncation errors. This also, in practice, allows time for adjustments to heading and airspeed to be made. Having a practical knowledge of the situation under consideration is vital in choosing a reasonable time step (Rumpfkeil and Zingg 2010).

Travelling from LHR to JFK against a headwind, the fixed final time is set to 29 000 s, giving \(N=290\), whilst in the opposite direction this is reduced to just 22 000 s, with \(N=220\). These times have been chosen following research into time optimal routes across the same winter period (Wells et al. 2021). They allow flights on all days enough time to reach their destination, whilst also lying between the longest and shortest scheduled flight times given by the airlines for this route between 1st December, 2019 and 29th February, 2020.

For the interior point algorithm the step tolerance was set to \(1\times 10^{-6}\), and the optimality tolerance to \(1\times 10^{-3}\). These values were shown to allow efficient convergence across all wind fields considered.

Given the time restriction on trajectories, the fixed airspeed yielding the minimum fuel use will depend on the daily wind field. For this reason, fuel use for trajectories flown at all airspeeds in increments of 1 \({{\text {m s}}^{-1}}\), within the operational constraints, was calculated and the trajectory results for the airspeed associated with the lowest fuel use for each day adopted. In some cases, this was the lowest airspeed allowing the trajectory to reach the destination target, whereas on days where winds were more favourable, the airspeed chosen depended on the most efficient airspeed for the model of aircraft used.

The initial airspeed across each time interval in the numerical model for OCP2, V(t), was chosen to be the airspeed obtained from OCP1, but by using the multistart solver, a range of other initial airspeeds was also applied. In the original formulation of OCP2, the airspeed is assumed to be \(V(t)\in {\mathbb {R}}\). However,there are obvious boundaries to an aircraft’s airspeed in the practical setting. In order to apply the fuel function based on the work of Poll and Schumann (2021a, b) across the range of temperatures recorded across the North Atlantic at cruise altitudes, it was necessary to have \(V(t)\in [199,252]\). This control constraint was applied in judging if a feasible solution had been found. In the case of westbound flights, optimised airspeeds varied between 199 and 242 \({{\text {m s}}^{-1}}\) and for eastbound flights this range was from 199 to 240 \({{\text {m s}}^{-1}}\), so in all cases a vector of feasible airspeeds was retrieved from the numerical optimisation.

In solving both OCP1 and OCP2 an initial vector of heading angles is required to produce the first trajectory. The GCR is now considered for the journey between the airports. The GCR between the departure and destination airports is divided into N equal length intervals for flights and the rhumbline angle that would take an aircraft from the start to the end of each interval in a no-wind scenario is calculated. (Rhumbline angles provide a single heading on which to travel between two points on the surface of a sphere and are calculated here using the Matlab mapping toolbox.) These angles form the estimate for \(\psi\).

4.2 Daily results from each numerical model

Results for the numerical solution shown in Sect. 2 are obtained as a vector of optimal headings and a value for the fuel used along the trajectory for each of the 91 days from 1st December, 2019 to 29th February, 2020. The headings are used to generate the states. The area spanned by these states and eight example routes can be seen for all days in Figs. 4 and 5. The shaded area shows the extent of the most extreme trajectory positions across the time period; not all points within this area will have formed part of a trajectory. Westbound flight routes obtained using just the heading angle as a control cover an area that stretches further South than those where time of arrival can be guaranteed by changes to both airspeed and heading angle. The extent of flight routes with varying airspeed also covers an area further North at the start of the flight, benefiting from the variable airspeed to allow a deviation into lower headwind regions. Eastbound flights with variable airspeed can be seen to avoid diversions to both North and South as they approach LHR. However, the area spanned by the trajectories is very similar whether just heading angle or heading angle and airspeed vary.

Fig. 4
figure 4

Plots showing region spanned by all fuel optimal trajectories across the North Atlantic for 1st December, 2019 to 29th February, 2020 found from the solution of OCP1, with 8 example routes in each direction shown. The shaded area shows the extent of trajectories, but not all points within the area are part of a route

Full size image
Fig. 5
figure 5

Plots showing region spanned by all fuel optimal trajectories across the North Atlantic for 1st December, 2019 to 29th February, 2020 found from the solution of OCP2, with 8 example routes in each direction shown. The shaded area shows the extent of trajectories, but not all points within the area are part of a route

Full size image

Percentile plots, shown in Figs. 6 and 7, display the percentage of flights passing to the South of each particular area of the North Atlantic. Outlying waypoints, those that have longitudes passed through by fewer than three of the flights, are shown as yellow crosses. All but one or two flights stayed within a longitude range of \(1-73~^\circ\)W.

These graphs are created by taking longitudes between the maximum and minimum longitudes of all flight trajectories generated in 1\(^{\circ }\) increments and then interpolating to find the corresponding latitudes for each daily trajectory. Percentiles for the latitudes at each longitude are found and these are plotted. This demonstrates the distribution of latitude positions across all routes and allows for easier comparison between the trajectories resulting from OCP1 and 2.

Flying West (Fig. 6) it can be seen that the range of latitudes at each longitude is wider for OCP1, but that the interquartile ranges are very similar. More of the OCP2 flights tend to fly further North across the middle of the Atlantic as they can vary their airspeed to counter headwinds and then slow down in more favourable regions of the wind field in order to adhere to the fixed journey time and save on fuel. The 1% percentile for the OCP1 flights demonstrates that at all latitudes certain journeys must go very far south to avoid headwinds to balance the need for both a prompt arrival at the target and a low fuel burn rate.

Figure 7 shows that the vast majority of flights going East follow a path very close to the GCR. Using two controls allows a small percentage of flights to go further North or South than the flights constrained by a fixed airspeed. The interquartile range of latitudes is also wider for flights with variable airspeed.

Fig. 6
figure 6

Plots showing percentiles of latitude positions for a set of integer longitude positions ranging between the furthest easterly and westerly points in the westbound trajectories obtained from OCP1 and 2. Waypoints at longitudes not accessed by all flights are shown in yellow

Full size image
Fig. 7
figure 7

Plots showing percentiles of latitude positions for a set of integer longitude positions ranging between the furthest easterly and westerly points in the westbound trajectories obtained from OCP1 and 2. All longitudes were accessed by all flights

Full size image

4.3 Comparison of fuel use between OCP1 and OCP2

If airspeed is fixed at a level that allows all daily flights to arrive at the target in the appropriate fixed time, then clearly more fuel will be used than by flights with a variable airspeed. In this case the highest airspeed used by any of the eastbound flights in the OCP1 formulation was 240 \({{\text {m s}}^{-1}}\) and for the westbound flights it was 241 \({{\text {m s}}^{-1}}\). Interestingly the most efficient fixed airspeed for the fixed time crossing between the two airports in a zero wind field, with a constant International Standard Atmosphere temperature of 221\(^\circ \mathrm{K}\), would be 252 \({{\text {m s}}^{-1}}\) flying East in the 22 000 s time window and 200 \({{\text {m s}}^{-1}}\) flying West in a fixed time of 29 000 s. Given that one of the key defining points of this research is to create trajectories with a fixed time across an entire winter season, these results demonstrate the importance of adapting to the daily wind field within this system. If, instead of varying the OCP1 airspeed on a daily basis, the maximum OCP1 airspeeds were used for all days in the 2019 -2020 winter season, by comparison the variable airspeed model used in OCP2 would save an average of 8% of the fuel. However, this can be viewed as unnecessarily high, as the fixed airspeed in OCP1 can be lowered to navigate the wind field specific to the day of flight. By analysing data from the solution of the approximate numerical methods for both OCP1 and OCP2, we can provide an estimate of the improvement in fuel efficiency when comparing the most efficient fixed airspeed flights each day to the corresponding most efficient variable airspeed flights.

Comparing results from the solution of OCP1 and OCP2, relative differences of 0.5% across the winter period are possible. On particular days, these savings are just under 4%. Figure 8 shows the percentage fuel saving made each day by using both airspeed and heading angle as control variables in each direction rather than just heading angle. The savings vary on a daily basis, so it is clear that the wind field is instrumental in dictating the importance of varying the airspeed for a fixed time flight.

Fig. 8
figure 8

Bar charts to show percentage of fuel from using the single control variable of heading angle saved by using two control variables, both heading angle and airspeed

Full size image

When viewed as a box and whisker plot, Fig. 9, the distribution of savings can be compared across the eastbound and westbound routes. Whilst median values are similar, the range of eastbound savings is smaller (excluding outliers) as is expected from a route that is most often benefiting from tailwinds, rather than fighting headwinds.

Fig. 9
figure 9

Box and whisker plot to compare distribution of percentage savings made by using OCP2 as the problem formulation rather than OCP1, for all 91 days of the winter of 2019 to 2020, for both eastbound and westbound flights

Full size image

Figure 10 shows the distribution of actual fuel savings made each day by using both airspeed and heading angle. Here it can be seen that in absolute terms the median fuel saving of eastbound flights is lower than that of westbound flights.

Fig. 10
figure 10

Box and whisker plot to compare distribution of absolute savings made by using OCP2 as the problem formulation rather than OCP1, for all 91 days of the winter of 2019 to 2020, for both eastbound and westbound flights

Full size image

Flying West just under 23 tonnes of fuel could be saved over the 91 days, whilst flying East fuel savings amount to over 15 tonnes. This gives a total fuel savings across the winter period for nineteen flights in each direction per day of 723 tonnes. These savings are a clear indication that when planning fixed time trajectories, varying the airspeed and the heading angle will give more efficient results in terms of fuel usage and thus emissions reduction, than controlling heading angle alone.

A comparison of routes generated from the time optimal model used in Wells et al. (2021), the fixed time fuel optimal model with both a single control variable and with two control variables developed in this paper and actual flight routes flown on the 12th December, 2019 is shown in Fig. 11. The 12th December, 2019 was chosen as a typical day on which a large number of flights were scheduled. From these plots it appears that most airlines prefer to use a path close to the time optimal route and the fuel optimal route, based on two controls. The fuel optimal route which depends purely on altering the heading angles can be seen to be very different from these. In this simplified model, if strong tailwinds are encountered the aircraft must deviate from a more direct path to avoid an early arrival at the destination airport, as the airspeed is fixed throughout the trajectory. These trajectories are representative of those obtained across the winter season considered. Airlines currently try to minimise their operating cost, which is made up of both fuel and time factors. However, trying to adhere to the timetable is also important. On this day 14 of the 19 westbound flights were more than 15 minutes early, with 10 of these being more than 30 minutes early and 3 being more than 45 minutes early. Eastbound all 18 flights were more than 45 minutes early, with 13 being over an hour early and 1 arriving an hour and a half early. Although airlines prefer to be early than late, such early arrival times can lead to added costs. Often aircraft are slowed and stacked as they approach the airport or extra waiting time is spent on the tarmac before accessing a gate, which is unpopular with customers and can lead to compensation claims (John 2020). From an operations point of view it can lead to blocked gates and ground crew, baggage handlers and fuel bowsers being in the wrong place.

Fig. 11
figure 11

Route maps showing constant airspeed time optimal trajectory (Wells et al. 2021), constant airspeed fuel optimal trajectory (OCP1), varying airspeed fuel optimal trajectory (OCP2), the great circle route (GCR) and actual flights for the 12th December, 2019

Full size image

The time optimal routes are simulated as flown at 250 \({{\text {m s}}^{-1}}\). The fuel optimal routes with fixed airspeed are simulated as flown at 238 \({{\text {m s}}^{-1}}\) going West and 204 \({{\text {m s}}^{-1}}\) going East, which are the most fuel efficient airspeeds for a fixed time flight from the OCP1 formulation on that day. All simulated routes are considered at a fixed altitude of approximately 34 000 feet, with a variable mass. The fuel optimization is calculated for a Boeing 777-236(ER). However, the actual flights are not fixed time, mass, altitude or airspeed and use a variety of aircraft. They are, though, restricted to the organised track system across the North Atlantic, so the flight path taken does not always reflect the airline’s chosen route. At a particular flight time, aircraft are given waypoints across the North Atlantic, which must define their routes, in order to maintain a safe separation between all aircraft in the vicinity, given the limited situational awareness before the advent of the new satellite communications. These waypoints can lead to aircraft following less time and fuel efficient routes (Wells et al. 2021).

4.4 Effect of wind field on optimised airspeed

As the airspeed control allows quite significant fuel savings on some days compared to optimization by controlling heading angle alone, but far smaller savings on other days, a link between daily wind conditions and airspeed variation is sought. Whilst it is true that mass and airspeed are also connected, with airspeed reducing with mass across a single trajectory in the absence of winds, this pattern is accounted for in the averaging of daily airspeed in the current analysis.

The winds along the GCR are used as a measure of likely headwinds and tailwinds experienced during a flight. These are calculated by splitting the GCR between LHR and JFK into 290 intervals for a westbound flight and 220 intervals for an eastbound flight. The rhumbline angle, \(\beta\), needed to fly directly between each pair of waypoints is calculated. The wind field for each day is interpolated to give zonal and meridional winds, u and v, at each waypoint. The sum of the components of these lying along the rhumbline angle for each interval of the GCR gives the tailwind, \(\tau\) at each waypoint.

$$\begin{aligned} \tau =\begin{bmatrix} u~v \end{bmatrix} \begin{bmatrix} \cos {\beta }\\ \sin {\beta } \end{bmatrix} \end{aligned}$$
(26)

By plotting airspeed for the OCP1 simulations and average airspeed for the OCP2 simulations each day against average daily tailwind, the effect of the wind field on the airspeed can be seen.

For westbound flights, shown in Figs. 12a and c, as the headwind strengthens, the aircraft must fly faster to make up time, so there is a negative correlation at the 5% significance level, with a product moment correlation coefficient of −0.8. For eastbound flights, shown in Figs. 12b and d, there is a similar negative correlation at the 5% significance level, but with product moment correlation coefficients of −0.9. This shows that the aircraft fly more slowly as they have a set time to reach their destination and the tailwind can help to minimise fuel burn, by avoiding the need for higher, less fuel efficient airspeeds.

Fig. 12
figure 12

Scatter graphs to show variation of OCP1 trajectory airspeed and average OCP2 trajectory airspeed each day with average tailwind along the GCR. Least squares regression line is shown with a 5% confidence interval

Full size image

The variation in airspeeds along a trajectory is also considered. However, as can be seen in Fig. 13 there is not enough evidence to say whether a link exists between the range of airspeeds and GCR average wind speed or not.

Fig. 13
figure 13

Scatter graphs to show variation of standard deviation of OCP2 trajectory airspeed each day with average tailwind along the GCR with least squares regression line and 5% confidence interval

Full size image

The airspeed changing along a trajectory in the context of a fixed time flight, has been shown to be a result of the winds encountered at each time step of the journey. To illustrate this effect further, the variation in airspeeds used along each daily fuel optimal trajectory is considered. Flying East on the 28th January, 2020 this variation is at its smallest and on the 25th January, 2020 it is at its most. On the 8th December, 2019 the westbound route has the largest variation in airspeeds, with the smallest variation on the 12th February, 2020.

In Figs. 14a and b the eastbound trajectories are shown, colour coded for airspeed, against a quiver plot of the wind field. On the 28th January, 2020, the route largely follows the wind direction from the middle of the North Atlantic, so airspeed can be reduced as the flight moves closer to LHR. However, at the start of the trajectory a higher airspeed is needed to fly perpendicular to the wind. This can be reduced as the route and the winds begin to come more into line between longitudes of 60\(^\circ\)W and 50\(^\circ\)W. On the 25th January, 2020 a smaller range of airspeeds is used as the flight is almost always flying in a direction that is not parallel to the wind vectors shown. This means that to arrive promptly, the aircraft must use higher airspeeds throughout. The only noticeable slowing occurs between the longitudes of 25\(^\circ\)W and 10\(^\circ\)W when the aircraft uses the vertical component of the wind to increase its latitude ready for the approach into LHR. This reinforces the previous finding, that stronger winds in the correct direction do mean that it is most efficient to use a larger range of airspeeds.

Fig. 14
figure 14

Fuel optimal trajectory maps showing airspeed change, in \({{\text {m s}}^{-1}}\)

Full size image

We now compare the westbound trajectories in Figs. 14c and d, on the 8th December, 2019 and the 12th February, 2020. During the first of these flights, a large range of airspeeds is used as the aircraft is able to fly further North and thus reach a patch of very weak winds for the majority of the flight. Having made good time across this central section, the aircraft can then slow down as it reaches the US coast. On the 12th February, 2020 the headwinds are stronger both as the aircraft leaves LHR and as it approaches JFK. This means that even across the centre of the North Atlantic a high airspeed must be maintained. From these examples the pattern from Fig. 13 is evident, with higher headwinds around the GCR leading to a smaller range of airspeeds being used to ensure fuel optimality.

5 Conclusions

In this paper a method is created to optimize fuel burn across a deterministic wind field for a fixed time of flight, using a novel fuel burn function. The time of flight is discretised into time steps. The altitude of the aircraft is assumed to be constant. This method involves controlling just the heading angle of the aircraft, or both the heading angle and the airspeed.

Flights are between LHR and JFK, with fixed times chosen to be slightly longer than the longest time optimal flight in each direction between these airports. The whole trajectory is assumed to be completed in cruise phase, as this makes up the vast majority of all transatlantic flights.

The fuel burn rate is calculated using a new physics based method (Poll and Schumann 2021a, b) and the flights are assumed to move through the deterministic wind fields supplied by the NCAR re-analysis data. Wind and temperature data at each time step is found by linearly interpolating the grid of weather data, which is at a 2.5\(^\circ\) resolution.

Results show that by including true airspeed as a second control up to 4% less fuel is used than when the flight is flown at constant airspeed. Over the course of all 91 days of the winter period, if nineteen flights were made each day (as was the case in 2019 to 2020), then just under 723 tonnes of fuel could be saved.

Links between airspeeds obtained from the fuel optimization using both heading and airspeed as controls and the daily wind conditions are established. Daily wind conditions are used to generate an average tailwind speed along the GCR. It is seen that as this tailwind increases, the average airspeed used falls. Although the range of airspeeds used along a trajectory is not strongly linked to the average tailwind around the GCR, there is a weak positive correlation which is further demonstrated using airspeed patterns for four example days.

Airspeed use along a flight path is plotted for the days with the highest and lowest standard deviations of airspeed flying both East and West. These flights are considered against the backdrop of the day’s wind field to show how the airspeed is adapted to make the best use of available winds.

As the time of flight is fixed for an entire season, on some days it will be far longer than for the corresponding time optimal trajectory. This means that despite using more fuel efficient airspeeds, fixing the time of flight will consume more fuel over all, than using a time optimal route. This does assume, however, that time optimal flights are able to land and passengers disembark immediately they arrive at their destination, which in practice is not always the case. As tarmac delays are treated identically for late and early arrivals at an airport, arriving too early can also be costly for airlines.

Future research should incorporate more diverse routes and aircraft models, as well as turbulence avoidance, given the projected increase in more severe turbulence with climate change (Williams and Joshi 2013; Williams 2017; Storer et al. 2017; Lee et al. 2019). The use of dynamic programming to ensure sufficient conditions for an optimal route is also of interest as the current method, uses a numerical global search function and so cannot guarantee optimality.