Skip to main content
SpringerLink
Log in

Inexact Hessian-vector products in reduced-space differential-equation constrained optimization

  • Published:
Optimization and Engineering Aims and scope Submit manuscript

Abstract

Reduced-space inexact-Newton–Krylov (RSNK) algorithms provide a modular and scalable framework for solving differential-equation-constrained optimization problems; thus, this class of algorithms provides an attractive compromise between poorly scaling “black-box” methods and more intrusive, full-space optimization algorithms. One of the challenges of implementing RSNK methods is the efficient solution of the linear subproblems, which involve the reduced Hessian. This paper explores inexact Hessian-vector products to improve the efficiency of these subproblems. The reduced-Hessian-vector products, which are required by the Krylov solver in RSNK, can be determined by solving two second-order adjoint equations. To reduce computational cost, we consider the approximate (i.e. inexact) solution of the second-order adjoints. We present bounds for the second-order adjoint tolerances that ensure the Hessian-vector product remains sufficiently accurate for inexact-Krylov methods. The bounds involve the 2-norm of the state and first-order adjoint sensitivities, and we provide an inexpensive Lanczos algorithm to estimate these matrix norms. Using numerical experiments, we investigate the proposed RSNK algorithm and compare it to other optimization algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. More precisely, they simplified the objective function in order to simplify the Hessian.

  2. In the context of DE-constrained optimization, the Lagrange multipliers are typically called the adjoint variables, and this is the convention adopted here.

  3. Again, we drop the Newton subscript \(k\).

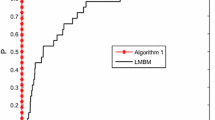
  4. Both reduced-space algorithms exhibit a drop in cost at 60 design variables: we have no explanation for this behaviour at this time.

References

  • Akçelik V, Biros G, Ghattas O (2002) Parallel multiscale Gauss–Newton–Krylov methods for inverse wave propagation. SC Conference, p. 41 doi:10.1109/SC.2002.10002

  • Akçelik V, Biros G, Ghattas O, Hill J, Keyes D, van Bloemen Waanders B (2006) Parallel algorithms for PDE-constrained optimization. In: Heroux MA, Raghavan P, Simon HD (eds) Parallel processing for scientific computing, chap. 16. Society for Industrial and Applied Mathematics, pp 291–322. doi:10.1137/1.9780898718133.ch16

  • Anderson JD (1991) Fundamentals of aerodynamics, 2nd edn. McGraw-Hill Inc., New York

    Google Scholar 

  • Arnold DN, Brezzi F, Cockburn B, Marini LD (2002) Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J Numer Anal 39(5):1749–1779. doi:10.1137/s0036142901384162

    Article  MathSciNet  MATH  Google Scholar 

  • Biros G, Ghattas O (2005) Parallel Lagrange–Newton–Krylov–Schur methods for PDE-constrained optimization. Part I: The Krylov–Schur solver. SIAM J Sci Comput 27:687–713

    Article  MathSciNet  MATH  Google Scholar 

  • Biros G, Ghattas O (2005) Parallel Lagrange–Newton–Krylov–Schur methods for PDE-constrained optimization. Part II: The Lagrange–Newton solver and its application to optimal control of steady viscous flows. SIAM J Sci Comput 27:714–739

    Article  MathSciNet  MATH  Google Scholar 

  • Borzì A, Schulz V (2011) Computational optimization of systems governed by partial differential equations. Society for Industrial and Applied Mathematics, pp. 47–48 doi:10.1137/1.9781611972054

  • Borzì A, Schulz V (2011) Computational optimization of systems governed by partial differential equations. Society for Industrial and Applied Mathematics, pp 62–66. doi:10.1137/1.9781611972054

  • Bouras A, Frayssé V (2005) Inexact matrix-vector products in Krylov methods for solving linear systems: a relaxation strategy. SIAM J Matrix Anal Appl 26(3):660–678. doi:10.1137/s0895479801384743

    Article  MathSciNet  MATH  Google Scholar 

  • Braack M (2009) Optimal control in fluid mechanics by finite elements with symmetric stabilization. SIAM J Control Optim 48(2):672–687. doi:10.1137/060653494

    Article  MathSciNet  MATH  Google Scholar 

  • Byrd RH, Curtis FE, Nocedal J (2008) An inexact SQP method for equality constrained optimization. SIAM J Optim 19(1):351–369. doi:10.1137/060674004

    Article  MathSciNet  MATH  Google Scholar 

  • Byrd RH, Curtis FE, Nocedal J (2010) An inexact Newton method for nonconvex equality constrained optimization. Math Program 122(2):273–299. doi:10.1007/s10107-008-0248-3

    Article  MathSciNet  MATH  Google Scholar 

  • Carpenter MH, Gottlieb D, Abarbanel S (1994) Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: methodology and application to high-order compact schemes. J Comput Phys 111(2):220–236. doi:10.1006/jcph.1994.1057

    Article  MathSciNet  MATH  Google Scholar 

  • Conn AR, Gould NIM, Toint PL (2000) Trust region methods. Society for Industrial and Applied Mathematics doi:10.1137/1.9780898719857

  • Dembo RS, Eisenstat SC, Steihaug T (1982) Inexact Newton methods. SIAM J Numer Anal 19(2):400–408. doi:10.1137/0719025

    Article  MathSciNet  MATH  Google Scholar 

  • Du X, Sarkis M, Schaerer CE, Szyld DB (2013) Inexact and truncated parareal-in-time Krylov subspace methods for parabolic optimal control problems. Electron Trans Numer Anal 40:36–57

    MathSciNet  MATH  Google Scholar 

  • Farin GE (1997) Curves and surfaces for computed aided geometric design: a practical guide, 4th edn. Academic Press, Inc, London

    Google Scholar 

  • Feng D, Pulliam TH (1995) An all-at-once reduced hessian SQP scheme for aerodynamic design optimization. Tech. Rep. RIACS-TR-95.19, NASA Ames Research Center, Moffett Field, California

  • Fletcher R (2000) Practical methods of optimization, 2nd edn. A Wiley-Interscience Publication, Wiley, New York

    Book  Google Scholar 

  • Frank PD, Shubin GR (1992) A comparison of optimization-based approaches for a model computational aerodynamics design problem. J Comput Phys 98(1):74–89

    Article  MATH  Google Scholar 

  • Funaro D, Gottlieb D (1988) A new method of imposing boundary conditions in pseudospectral approximations of hyperbolic equations. Math Comput 51(184):599–613

    Article  MathSciNet  MATH  Google Scholar 

  • Gatsis J, Zingg DW (2003) A fully-coupled Newton–Krylov algorithm for aerodynamic optimization. In: 16th AIAA Computational Fluid Dynamics Conference, AIAA-2003-3956. Orlando.

  • Ghate D, Giles M (2007) Efficient Hessian calculation using automatic differentiation. In: 25th AIAA Applied Aerodynamics Conference, AIAA-2007-4059. Miami. doi:10.2514/6.2007-4059

  • Golub GH, Ye Q (1999) Inexact preconditioned conjugate gradient method with inner–outer iteration. SIAM J Sci Comput 21(4):1305–1320. doi:10.1137/s1064827597323415

    Article  MathSciNet  Google Scholar 

  • Griewank A, Walther A (2008) Evaluating derivatives: principles and techniques of algorithmic differentiation. Society for Industrial and Applied Mathematics http://www.worldcat.org/isbn/9780898716597

  • Griewank A, Walther A (2008) Evaluating derivatives: principles and techniques of algorithmic differentiation, chap. 5. Society for Industrial and Applied Mathematics, pp. 91–105. http://www.worldcat.org/isbn/9780898716597

  • Gunzburger MD (2003) Perspectives in flow control and optimization. Society for Industrial and Applied Mathematics http://www.worldcat.org/isbn/9780898715279

  • Haber E, Ascher UM (2001) Preconditioned all-at-once methods for large, sparse parameter estimation problems. Inverse Probl 17(6):1847–1864. doi:10.1088/0266-5611/17/6/319

    Article  MathSciNet  MATH  Google Scholar 

  • Hartmann R (2007) Adjoint consistency analysis of discontinuous Galerkin discretizations. SIAM J Numer Anal 45(6):2671–2696. doi:10.1137/060665117

    Article  MathSciNet  MATH  Google Scholar 

  • Heinkenschloss M, Vicente LN (1999) An interface optimization and application for the numerical solution of optimal control problems. ACM Trans Math Softw 25(2):157–190. doi:10.1145/317275.317278

    Article  MathSciNet  MATH  Google Scholar 

  • Hicken JE, Alonso JJ (2013) Comparison of reduced- and full-space algorithms for PDE-constrained optimization. In: 51st AIAA aerospace sciences meeting, AIAA-2013-1043. Grapevine. doi:10.2514/6.2013-1043

  • Hicken JE, Zingg DW (2011) Superconvergent functional estimates from summation-by-parts finite-difference discretizations. SIAM J Sci Comput 33(2):893–922. doi:10.1137/100790987

    Article  MathSciNet  MATH  Google Scholar 

  • Hicken JE, Zingg DW (2011) The role of dual consistency in functional accuracy: error estimation and superconvergence. In: 20th AIAA computational fluid dynamics conference, AIAA-2011-3855. Honolulu.

  • Hicken JE, Zingg DW (2012) Dual consistency and functional accuracy: a finite-difference perspective. J Comput Phys 256:161–182

    Article  MathSciNet  Google Scholar 

  • Hinze M, Pinnau R, Ulbrich M, Ulbrich S (2009) Optimization with PDE constraints. Springer, New York, pp 64–65. http://www.worldcat.org/isbn/9781402088384

  • Iollo A, Salas MD, Ta’asan S (1993) Shape optimization governed by the Euler equations using an adjoint method. Tech. Rep. ICASE 93–78, NASA Langley Research Center, Hampton.

  • Keyes DE (1995) Aerodynamic applications of Newton–Krylov–Schwarz solvers. In: Proceedings of the 14th international conference on numerical methods in fluid dynamics. Springer, New York, pp 1–20

  • Knoll DA, Keyes DE (2004) Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J Comput Phys 193(2):357–397. doi:10.1016/j.jcp.2003.08.010

    Article  MathSciNet  MATH  Google Scholar 

  • Kreiss HO, Scherer G (1974) Finite element and finite difference methods for hyperbolic partial differential equations. In: de Boor C (ed) Mathematical aspects of finite elements in partial differential equations. Mathematics Research Center, the University of Wisconsin Academic Press, Madison

  • Lanczos C (1950) An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J Res Natl Bur Stand 45(4):255–282

    Article  MathSciNet  Google Scholar 

  • Liu DC, Nocedal J (1989) On the limited memory BFGS method for large scale optimization. Math Program 45:503–528. doi:10.1007/BF01589116

    Article  MathSciNet  MATH  Google Scholar 

  • Lu JC (2005) An a posteriori error control framework for adaptive precision optimization using discontinuous Galerkin finite element method. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge

  • Martins JRRA, Sturdza P, Alonso JJ (2003) The complex-step derivative approximation. ACM Trans Math Softw 29(3):245–262. doi:10.1145/838250.838251

    Article  MathSciNet  MATH  Google Scholar 

  • Mattsson K, Svärd M, Nordström J (2004) Stable and accurate artificial dissipation. J Sci Comput 21(1):57–79

    Article  MathSciNet  MATH  Google Scholar 

  • Melvin RG, Huffman WP, Young DP, Johnson FT, Hilmes CL (1999) Recent progress in aerodynamic design optimization. Int J Numer Methods Fluids 30(2):205–206. doi:10.1002/(sici)1097-0363(19990530)30:2%3C205:aid-fld827%3E3.0.co;2-u

    Google Scholar 

  • Morales JL, Nocedal J (2000) Automatic preconditioning by limited memory quasi-Newton updating. SIAM J Optim 10(4):1079–1096. doi:10.1137/S1052623497327854

    Article  MathSciNet  MATH  Google Scholar 

  • Nocedal J, Wright SJ (2006) Numerical optimization, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  • Nocedal J, Wright SJ (2006) Numerical optimization, chap. 6, 2nd edn. Springer, Berlin

    Google Scholar 

  • Nocedal J, Wright SJ (2006) Numerical optimization, chap. 7, 2nd edn. Springer, Berlin

    Google Scholar 

  • Nocedal J, Wright SJ (2006) Numerical optimization, chap. 12, 2nd edn. Springer, Berlin

    Google Scholar 

  • Rumpfkeil MP, Mavriplis DJ (2010) Efficient Hessian calculations using automatic differentiation and the adjoint method with applications. AIAA J 48(10):2406–2417. doi:10.2514/1.j050451

    Article  Google Scholar 

  • Saad Y (1993) A flexible inner–outer preconditioned GMRES algorithm. SIAM J Sci Stat Comput 14(2):461–469

    Article  MathSciNet  MATH  Google Scholar 

  • Saad Y (2003) Iterative methods for sparse linear systems, chap. 6, 2nd edn. SIAM, Philadelphia

    Book  Google Scholar 

  • Saad Y (2011) Numerical methods for Large eigenvalue problems. Society for Industrial and Applied Mathematics. doi:10.1137/1.9781611970739

  • Saad Y, Schultz MH (1986) GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci Stat Comput 7(3):856–869

    Article  MathSciNet  MATH  Google Scholar 

  • Simoncini V, Szyld DB (2003) Theory of inexact Krylov subspace methods and applications to scientific computing. SIAM J Sci Comput 25(2):454–477. doi:10.1137/s1064827502406415

    Article  MathSciNet  MATH  Google Scholar 

  • Squire W, Trapp G (1998) Using complex variables to estimate derivatives of real functions. SIAM Rev 40(1):110–112

    Article  MathSciNet  MATH  Google Scholar 

  • Strand B (1994) Summation by parts for finite difference approximations for d/dx. J Comput Phys 110(1):47–67. doi:10.1006/jcph.1994.1005

    Article  MathSciNet  MATH  Google Scholar 

  • Ta’asan S, Kuruvila G, Salas MD (1992) Aerodynamic design and optimization in one shot. In: The 30th AIAA aerospace sciences meeting and exhibit, AIAA-1992-25

  • Waltz RA, Nocedal J (2003), KNITRO user’s manual. Northwestern University, Evanston, Technical, Report OTC-2003/5

  • Wang Z, Navon IM, Dimet FX, Zou X (1992) The second order adjoint analysis: theory and applications. Meteorol Atmos Phys 50:3–20. doi:10.1007/BF01025501

    Article  Google Scholar 

  • van den Eshof J, Sleijpen GLG (2004) Inexact Krylov subspace methods for linear systems. SIAM J Matrix Anal Appl 26(1):125–153. doi:10.1137/s0895479802403459

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The author thanks the anonymous referees for their careful reading of the manuscript and helpful remarks. The author gratefully acknowledges the financial support of Rensselaer Polytechnic Institute.

Author information

Authors and Affiliations

  1. Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY , 12180, USA

    Jason E. Hicken

Authors
  1. Jason E. Hicken
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jason E. Hicken.

Appendix: Optimization algorithms

Appendix: Optimization algorithms

figure b
figure c
figure d

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hicken, J.E. Inexact Hessian-vector products in reduced-space differential-equation constrained optimization. Optim Eng 15, 575–608 (2014). https://doi.org/10.1007/s11081-014-9258-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11081-014-9258-6

Keywords

Search

Navigation