Is there Consumer Risk-Pooling in the Open Economy? The Evidence Reconsidered

Abstract

We revisit the evidence on consumer risk-pooling and uncovered interest parity. Widely used single-equation tests are strongly biased against both. Using the full-model, Indirect Inference test, which is unbiased and has Goldilocks power according to Monte Carlo experiments, we find that both the risk-pooling hypothesis and its weaker UIP version are generally accepted as part of a full world DSGE model. The fact that the risk-pooling hypothesis, with its implication of strong cross-border consumer linkage, has passed this test with generally the highest p-value, suggests that it deserves serious attention from policy-makers looking for a relevant model with which to discuss international monetary and other business cycle policies.

1 Introduction

This paper reports on a searching empirical test of the consumer risk-pooling hypothesis, in many two-country currency set-ups. This hypothesis states that consumers make use of state-contingent bonds to insure themselves against shocks and that as a result the real exchange rate between two countries is closely correlated with the relative consumption of their residents. This can be shown formally – following Chari et al. (2002) – to be $\sigma (c_{t}-c_{t}^{\ast })=q_{t}-v_{t}$, where q_t is the log real exchange rate, c_t and $c_{t}^{\ast }$ are the log home and foreign consumptions, σ is the inverse of elasticity of intertemporal substitution of consumption, and v is the difference between the logs of the two countries’ time-preference errors. On this issue it is generally agreed that there is no evidence for the hypothesis or even for a weaker version (in which non-contingent bonds are used) in the form of uncovered interest parity (UIP) $E_{t}q_{t+1}-q_{t}=(R_{t}-E_{t}\pi _{t+1})-(R_{t}^{\ast }-E_{t}\pi _{t+1}^{\ast })$, where R_t ($R_{t}^{\ast }$) is the home (foreign) nominal interest rate, π_t+ 1 ($\pi _{t+1}^{\ast }$) is the home (foreign) inflation.¹ However, with highly sophisticated financial markets freely capable of providing insurance it has seemed a puzzle that existing evidence does not favour any version. The empirical testing in this work has been via predictive tests on the exchange rate based on single-equation regressions, where among others one of the main difficulties in assessing this evidence has been that all the variables in these regressions are endogenous.

This problem was circumvented by Minford et al. (2020) (MOZ hereafter) where they embedded the risk-pooling hypothesis and its weaker (UIP) variant in a full DSGE model and tested the model as a whole. The model took the familiar three-equation IS, Phillips Curve, Taylor Rule New Keynesian set-up of Clarida et al. (1999) extended to embrace the US, Europe and the rest of the world, essentially a two-country model for the US and EU which we briefly recap below. They used the method of Indirect Inference to estimate and test the two model versions for the US and the EU pair of economies. What they found was that both strong and weak hypotheses were accepted on the test, with risk-pooling the most probable. They accounted for the discrepancy between these findings and the rejection of both hypotheses in conventional single-equation tests by showing, in a Monte Carlo experiment on that two-country model, when either hypothesis was true, that certain widely-used single-equation tests would be heavily biased towards the hypotheses’ rejection.

The MOZ findings are a striking contrast to those by Burnside (2019) who rejected the UIP relation for a dozen pairs of industrialized economies on single-equation tests. They are a fundamental challenge to the ‘empirical consensus’ – now barely questioned – that UIP fails to fit, based on which many including Burnside attempt to solve the ‘puzzle’ with a variety of model features. In this paper, we question this consensus by providing a comprehensive assessment of the MOZ findings, applying the full-model, Indirect Inference test to the currency pairs examined by Burnside, which has never been done before. We find that, while Burnside spuriously rejects UIP in most cases , this hypothesis, as well as its strong form of consumer risk-pooling, are both generally accepted as part of a full model according to Indirect Inference. The two hypotheses perform about equally well, with one being slightly better than the other depending on the currency pair, and on average the stronger risk-pooling hypothesis having a somewhat higher probability. The unbiased MOZ method suggests generally opposite findings to what were found by the biased Burnside method, except in the rare cases of the EU (both accept), and New Zealand and Switzerland (both reject). What we find here therefore provides strong, rigorous evidence in favour of consumer risk-pooling and UIP. We argue that, given the important policy implications of these hypotheses, particularly risk-pooling, and the fact that both these hypotheses fit the data well, policy-makers engaged in issues in international monetary economics should take these hypotheses much more seriously.

The remainder of this paper is organized as the following: Section 2 recaps the model that formed the backdrop for the testing in MOZ; Section 3 explains the method of Indirect Inference; Section 4 sets out the findings on the selected currency pairs, side by side with the single-equation findings of Burnside (2019); Section 5 concludes.

2 The Full Model

The model we use is derived in detail in MOZ. There are three economies: the US, the foreign partner country (which in this exposition we call the EU), and the rest of the world (RoW) which is treated only as an entity trading with the two countries under current account balance, so that its imports are determined by its output, which in turn is determined by the countries’ demands for its exports. Each of the two country models is New Keynesian, consisting of an IS curve, a Phillips curve and a Taylor Rule. The derivations are standard: the IS curve is derived from the household Euler equation, which in turn is substituted into the output market-clearing equation for consumption, yielding a forward-looking output demand equation with terms in net exports and government spending.² A labour-only production function determines output from households’ labour supply and exogenous productivity; this gives rise to an exogenous trend output driven by productivity and an output gap reflecting variations in labour input around this trend, with firms’ marginal costs rising with the output gap, reflecting lower marginal productivity and rising real wages. The Phillips Curve for inflation is then derived under Calvo price rigidity, as a forward-looking function of expected future inflation and the output gap. The Taylor Rule captures the central bank’s interest rate setting behaviour. Finally, exports are set by other countries’ import demands for them, determined by their output and relative country prices.

The model is listed in ?? in full. In what follows we present the key equations seeing US as the home economy. All variables, except inflation and nominal interest rate, are measured in log. US variables have no superscipt, EU variables are asterisked, while world variables carry the RoW superscript. All equation errors are assumed to follow an AR(1) process.

US IS curve:

$$ \begin{array}{@{}rcl@{}} y_{t}&=&E_{t}y_{t+1}-c\frac{1}{\sigma }{\Theta} (R_{t}-E_{t}\pi_{t+1}-\bar{r} )-xz_{1}{\Theta} E_{t}{\Delta} y_{t+1}^{\ast }-xm_{2}{\Theta} E_{t}{\Delta} y_{t+1}^{RoW}\\&&-xz_{3}{\Theta} E_{t}{\Delta} q_{t+1}+\varepsilon_{t}^{IS} \end{array} $$

(1)

where y_t, $y_{t}^{\ast }$ and $y_{t}^{RoW}$ are the home, foreign and world output, respectively, $R_{t}-E_{t}\pi _{t+1}-\bar {r}$ is the home real interest rate, q_t is the $/EUR real exchange rate, c and x are the steady-state consumption and export ratios, and Θ, z₁ and z₃ are combinations of the structural parameters. $\varepsilon _{t}^{IS}$ is the equation error which can be interpreted as the demand shock.

US Phillips curve:

$$ \pi_{t}=\beta E_{t}\pi_{t+1}+\kappa_{a}\left( y_{t}-{y_{t}^{p}}\right) - \frac{\alpha }{1-2\alpha }\left[ \beta E_{t}(q_{t+1}-q_{t})-(q_{t}-q_{t-1}) \right] +\varepsilon_{t}^{PP} $$

(2)

where π_t is CPI inflation, $y_{t}-{y_{t}^{p}}$ is the ‘output gap’, β is the discount rate, α is the degree of openness, and κ_a is a function of structural parameters. $\varepsilon _{t}^{PP}$ is the supply shock.

US ‘potential output’:

$$ {y_{t}^{p}}-y_{t-1}^{p}={\Gamma}^{y^{p}}+\delta (y_{t-1}^{p}-y_{t-2}^{p})+\varepsilon_{t}^{yp} $$

(3)

where ${y_{t}^{p}}$ is let follow a random walk process with drift (${\Gamma }^{y^{p}}$), which reflects the permanent impact of the productivity shock ($\varepsilon _{t}^{yp}$).

US Taylor Rule:

$$ R_{t}=\rho R_{t-1}+(1-\rho )[\phi_{\pi }\pi_{t}+\phi_{y}(y_{t}-{y_{t}^{p}})]+\phi_{q}(q_{t}-q_{t}^{ss})+{\varepsilon_{t}^{R}} $$

(4)

where nominal interest rate responds to inflation (ϕ_π), output gap (ϕ_y) and the real exchange rate (ϕ_q) with policy inertia (ρ). $q_{t}^{ss}$ is the steady-state real exchange rate. $\varepsilon _{t}^{R}$ is the monetary policy error.

US import from the EU is assumed to be affected by the US income and the real exchange rate:

$$ im_{EU,t}^{US}=\mu y_{t}-\psi q_{t} $$

(5)

US import from the rest of the world is assumed to be only affected by the US income for simplicity:

$$ im_{W,t}^{US}=\nu y_{t} $$

(6)

The EU, the foreign economy here, has similar equations.

Trade balance of the world economy requires:

$$ {\Xi} im_{W,t}^{US}+(1-{\Xi} )im_{W,t}^{EU}=\digamma \cdot ex_{W,t}^{US}+(1-\digamma )ex_{W,t}^{EU} $$

(7)

where Ξ and $\digamma$ are the steady-state import/export ratios, and the LHS of the equation can be seen as the ‘world output’ $y_{t}^{RoW}={\Xi } im_{W,t}^{US}+(1-{\Xi } )im_{W,t}^{EU}$.

The world’s relative demand for US and EU products is given by:

$$ ex_{W,t}^{US}=ex_{W,t}^{EU}+\psi^{RoW}q_{t} $$

(8)

2.1 The Risk-Pooling and UIP Model Variants

Equations 1 – 8, plus the ‘foreign’ equations omitted for EU, constitute the simple ‘world’ model backdrop based on which we compare consumer risk-pooling and its weak form of UIP in the following. The two model variants can be derived, following Chari et al. (2002), as follows:

• full risk-pooling via state-contingent nominal bonds:

let the price at time t = 0 (when the state was x₀) of a home nominal state-contingent bond paying 1 (home currency) in state x_t be:

$$ n(x_{t},x_{0})=\beta f(x_{t},x_{0})\frac{U_{c}(x_{t},x_{0})}{P(x_{t},x_{0})}/ \frac{U_{c}(x_{0})}{P(x_{0})} $$

(9)

where β is time-preference and f(x_t,x₀) is the probability of x_t occurring given x₀ has occurred. Now note that foreign consumers can also buy this bond freely via the foreign exchange market (where S is home currency per foreign currency) and its value as set by them will be:

$$ n(x_{t},x_{0})=\beta f(x_{t},x_{0})\frac{U_{c}^{\ast }(x_{t},x_{0})S(x_{t},x_{0})}{P^{\ast }(x_{t},x_{0})}/\frac{U_{c}^{\ast }(x_{0})S(x_{0})}{P^{\ast }(x_{0})} $$

(10)

Here they are equating the expected marginal utility of acquiring this dollar bond with foreign currency, with the marginal utility of a unit of foreign currency at time 0. Plainly the price paid by the foreign consumer must be equal by arbitrage to the price paid by the home consumer. Equating these two equations yields:

$$ \frac{U_{c}(x_{t},x_{0})}{P(x_{t},x_{0})}/\frac{U_{c}(x_{0})}{P(x_{0})}= \frac{U_{c}^{\ast }(x_{t},x_{0})S(x_{t},x_{0})}{P^{\ast }(x_{t},x_{0}).}/ \frac{U_{c}^{\ast }(x_{0})S(x_{0})}{P^{\ast }(x_{0})} $$

(11)

Now we note that the terms for the period t = 0 are the same for all x_t so that for all t from t = 0 onwards:

$$ \frac{U_{c}(x_{t},x_{0})}{U_{c}^{\ast }(x_{t},x_{0})}=\kappa \frac{ P(x_{t},x_{0})S(x_{t},x_{0})}{P^{\ast }(x_{t},x_{0})} $$

(12)

where $\kappa =\frac {U_{c}(x_{0})}{P(x_{0})}/\frac {U_{c}^{\ast }(x_{0})S(x_{0})}{P^{\ast }(x_{0})}$ is a constant.

Let $U=C_{t}^{(1-\sigma )}\epsilon /(1-\sigma )$, $q_{t}=-p_{t}+p_{t}^{\ast }+s_{t}$ be the real exchange rate, and 𝜖 is the time-preference shock. Equation 12 implies:

$$ \sigma (c_{t}-c_{t}^{\ast })=q_{t}-v_{t} $$

(13)

ignoring the constant, which is the risk-pooling condition which we introduced at the beginning of the paper. v is the difference between the logs of the two countries’ time-preference errors (which will also form part of the two IS curve shocks).

To see that this implies the UIP relationship, use the Euler equations for consumption (e.g. for home consumers $c_{t}=-\frac {1}{\sigma }\left (\frac { R_{t}-E_{t}\pi _{t+1}}{1-B^{-1}}-\ln \epsilon _{t}\right )$ where B^− 1 is the forward operator keeping the date of expectations constant). Substituting for consumption into the risk-pooling condition gives us UIP:

$$ E_{t}q_{t+1}-q_{t}=(R_{t}-E_{t}\pi_{t+1})-(R_{t}^{\ast }-E_{t}\pi_{t+1}^{\ast }) $$

(14)

• when there are only non-contingent bonds then arbitrage forces UIP. When this is substituted back into the Euler equations it yields:

$$ \sigma (1-B^{-1})(c_{t}-c_{t}^{\ast })=(1-B^{-1})(q_{t}-v_{t}) $$

(15)

Hence now the risk-pooling condition occurs in expected form from where it currently is. But any shocks may disturb it in the future.

Thus with full risk-pooling under state-contingent bonds relative consumption is exactly correlated with the real exchange rate and time-preference shocks. But under non-contingent bonds it is subject to all shocks: it is only expected to be correlated exactly from where it currently is.

Our risk-pooling variant of the world model therefore combines (1) - (8), the ‘foreign’ equations, and the ‘RP’ Eq. 13 where c_t and $c_{t}^{\ast }$ are derived from outputs and net exports using the market-clearing equations. The UIP variant of the model replaces the RP equation with the UIP (14).

3 The Method of Indirect Inference

Indirect inference has been widely used in applied macroeconomics. Early applications can be dated back to Smith (1993), Gregory and Smith (1991, 1993), Gourieroux et al. (1993), Gourieroux and Monfort (1996) and Canova (2005). The method was originally designed for estimating a structural model when the model’s likelihood function (based on which ‘direct’ inferences can be implied) is too complex for regular algorithms to find the optimal parameter values. The basic idea is to first use an auxiliary model whose likelihood function is relatively simple for referential, indirect inferences to be found; the algorithm then searches for the parameter values of the structural model that enable the structural model to best replicate the inferences implied by the auxiliary model.

The method has been substantially developed by Minford et al. (2008) and Meenagh et al. (2009), Le et al. (2011, 2016) and Minford et al. (2019) in recent years for it to be used as a formal statistical test on an already estimated or calibrated model. The widely used Bayesian method with set priors does not test whether a model fits the data; rather, it assesses the model’s likelihood, including that flowing from the priors, which in open economy macroeconomics remain too controversial to impose with general agreement to their truth. The DSGE-VAR method (Del Negro and Schorfheide 2006) evaluates the absolute fit; however it is not a statistical test and therefore, provides no indication as to when to reject/accept a model. Maximum Likelihood estimation can provide a likelihood test of data fit. But Le et al. (2016) show, by Monte Carlo experiment on macro models, that ML estimation in small samples is highly biased, as is well-known, and that likelihood tests suffer from low power compared with indirect inference tests.

The idea of testing with indirect inference is to first describe the data behaviour in the sample by the auxiliary model, for which we use a VARX below. It then simulates the structural model, our DSGE model here, by bootstrapping its innovations to create parallel simulations from each of which implied auxiliary model estimates are found, generating a distribution of them according to the DSGE model. It then asks whether the VARX estimates found with the actual data came from this distribution with a high enough probability to pass the Wald test.

In our practice of testing the RP and UIP hypotheses we are interested in the models’ capacity in accounting for the international business cycle dynamics, for which we use a VARX of the two outputs for each currency pair:

$$ Y_{t}=AY_{t-1}+BX_{t-1}+e_{t} $$

(16)

where $Y_{t}\equiv (y_{t},y_{t}^{\ast })^{\prime }$, $X_{t}\equiv ({y_{t}^{p}},y_{t}^{p\ast },t)^{\prime }$ where ${y_{t}^{p}}$ ($y_{t}^{p\ast }$) are the home (foreign) potential outputs measured with HP trends of y_t ($y_{t}^{\ast }$), t is the deterministic trend, e_t is the error vector, and A and B are the coefficient matrices. The Wald test statistic is calculated by:

$$ Wald=({\Phi}_{T}-\overline{\Phi })^{\prime }\sum\nolimits_{({\Phi} {\Phi} )}^{-1}({\Phi}_{T}-\overline{\Phi }) $$

(17)

where Φ_T is the vector of VARX estimates implied by the actual data, and $\overline {\Phi }$ and ${\sum }_{({\Phi } {\Phi } )}$ are the mean and variance-covariance matrix, respectively, of the vectors implied by the simulated samples. We let these vectors include both the autoregressive coefficients and the variances of the VARX residuals, such that both the dynamic behaviour and the volatility of the data are allowed for. Our test has the null hypothesis H₀ being ‘the model being tested is ‘true”. The p-value of the test is calculated by:

$$ p=(100-WP)/100 $$

(18)

where WP is the percentile of the Wald statistic found with the actual data in the distribution of it generated by the simulated samples. The models would pass/fail the Wald test if their p-value is above/below the 1%, 5% or 10% threshold.

The test is generally found to be unbiased and powerful by Monte Carlo experiments. Among others, MOZ verify that a model like ours would be rejected for 5% of the time – if the 5% threshold is used – when the model is true. However, when the model is falsified by up to 5%, it would be always rejected at the 5% level.³ Hence a false model, even if just slightly falsified, is unlikely to pass the rigorous test of Indirect Inference.

3.1 Determining the Test Composition

Here we carefully go over the exact test we use. To explain this, we replicate the Monte Carlo experiment of MOZ and extend it to review the power of our test against errors specifically in the UIP and RP equations, in order to discuss carefully the test details.

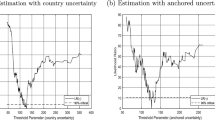
Indirect inference testing requires one to choose which variables’ behaviour should enter the auxiliary model to give the test optimal power: by including a wide selection the power becomes extremely high, implying that no tractable model can pass, while too narrow a selection can drive power too low. We chose the two country outputs, y_t and $y_{t}^{\ast }$, as giving the optimal power. We also considered including the real exchange rate, q_t, as well or instead. Figure 1 shows the power of our chosen test with the two outputs both against general model parameter errors and against specific parameter errors in the UIP and RP equations (To falsify these last two equations we introduced a false constant and slope parameter as follows: a) For the UIP (14), a and b are varied from their true values a = 0, b = 1 by +/- x% alternately: $(E_{t}q_{t+1}-q_{t})=a+b\left [ (R_{t}-E_{t}\pi _{t+1})-(R_{t}^{\ast }-E_{t}\pi _{t+1}^{\ast })\right ]$; b) For the RP (13), a and b are varied from their true values a = 0, $b=\frac {1}{\sigma }$ (= 1.595 as in MOZ) by +/- x% alternately: $(c_{t}-c_{t}^{\ast })=a+bq_{t}- \frac {1}{\sigma }v_{t}$).

Fig. 1

Power of the test by Monte Carlo experiments

It turns out that testing against the two outputs as well as the real exchange rate drives the power to excessive levels, with high chances of model rejection with only slight parameter errors, while testing against the real exchange rate instead has inadequate power, especially against errors in the UIP and RP equations themselves. Testing against the two outputs alone offers Goldilocks power, as it exhibits good, but not excessive, power both generally across the whole model and specifically in the UIP and RP equations which are key model equations. It is these two outputs that we use for testing the currency pairs in the next section.

4 Empirical Results for Country Currency Pairs

We now show the results for our indirect inference tests on the ten country currency pairs considered by Burnside (2019), using pretty much the same sample period (1971Q1 and 2018Q4). The p-values of all these tests are reported in Table 1.

Table 1 P-values of RP and UIP in country pairs

What we see is that, while UIP is mostly rejected by the single-equation test of Burnside, it, as well as its strong form of consumer risk-pooling, are widely accepted by the full-model test of Indirect Inference. This divergence, as we explained at the beginning of this paper, is likely to be due to the bias of the single-equation test towards the hypothesis’ rejection, which is a small sample bias as MOZ have pointed out. When this bias is corrected by full-model Indirect Inference, as we see here, the UIP hypothesis is mostly accepted (Of course some rejections will occur by chance): we find that using the full-model test UIP is rejected in only four cases (Denmark, New Zealand, Sweden and Switzerland) and risk-pooling in only three (the last three listed), whereas using the single-equation test UIP is rejected in eight cases, i.e., 80%.

Overall, on this issue the full-model test of Indirect Inference suggests quite opposite findings to what would be suggested by the single-equation test. However there are a few exceptions: both tests accept the hypothesis in the case of the EU; in the cases of New Zealand and Switzerland, by contrast, both tests reject the hypothesis. Interestingly, the hypothesis is rejected by Indirect Inference for Sweden where it is accepted by the single-equation test even though the latter generally over-rejects. For the rest, the majority of currency pairs accepted by Indirect Inference, we find that risk-pooling and UIP are both good model assumptions, with risk-pooling typically having the higher p-value.

What we find here, therefore, suggests that previous evidence rejecting consumer risk-pooling and UIP may be the unfortunate result of the bias in tests with single-equation regressions.

5 Conclusion

Previous statistical tests of both consumer risk-pooling and UIP based on single-equation regressions are likely to reject these hypotheses spuriously. In this paper we test them as part of a full world DSGE model, using the method of Indirect Inference. We found that both the risk-pooling hypothesis and its weaker UIP version are generally accepted in these full-model tests that avoid the bias involved in the single equation tests that previously widely rejected them, with the risk-pooling hypothesis found to be somewhat the more probable on average.

This is to our knowledge the first time that a powerful statistical test like Indirect Inference has been performed on currency data across so many markets. The fact that the risk-pooling hypothesis, with its implication of strong cross-border consumer linkage, has passed this test with generally the highest p-value, suggests that it deserves serious attention from policy-makers looking for a relevant model with which to discuss international monetary and other business cycle policies.

Appendix: : Listing of model

• US

IS curve:

$$ \begin{array}{@{}rcl@{}} y_{t}&=&E_{t}y_{t+1}-c\frac{1}{\sigma }{\Theta} (R_{t}-E_{t}\pi_{t+1}-\bar{r} )-xz_{1}{\Theta} E_{t}{\Delta} y_{t+1}^{\ast }-xm_{2}{\Theta} E_{t}{\Delta} y_{t+1}^{RoW}\\&&-xz_{3}{\Theta} E_{t}{\Delta} q_{t+1}+\varepsilon_{t}^{IS} \end{array} $$

(A.1)

Phillips curve:

$$ \pi_{t}=\beta E_{t}\left( \pi_{t+1}\right) +\kappa_{a}\left( y_{t}-{y_{t}^{p}}\right) -\frac{\alpha }{1-2\alpha }\left[ \beta E_{t}(q_{t+1}-q_{t})-(q_{t}-q_{t-1})\right] +\varepsilon_{t}^{PP} $$

(A.2)

Taylor rule:

$$ R_{t}=\rho R_{t-1}+(1-\rho )[\phi_{\pi }\pi_{t}+\phi_{y}(y_{t}-{y_{t}^{p}})]+\phi_{q}(q_{t}-q_{t}^{ss})+{\varepsilon_{t}^{R}} $$

(A.3)

Productivity:

$$ {y_{t}^{p}}-y_{t-1}^{p}={\Gamma}^{y^{p}}+\delta (y_{t-1}^{p}-y_{t-2}^{p})+\varepsilon_{t}^{yp} $$

(A.4)

US import from EU:

$$ im_{EU,t}^{US}=\mu y_{t}-\psi q_{t} $$

(A.5)

US import from RoW:

$$ im_{W,t}^{US}=\nu y_{t} $$

(A.6)

• EU

IS curve:

$$ \begin{array}{@{}rcl@{}} y_{t}^{\ast }&=&E_{t}y_{t+1}^{\ast }-c^{\ast }\frac{1}{\sigma^{\ast }}{\Theta}^{\ast }(R_{t}^{\ast }-E_{t}\pi_{t+1}^{\ast }-\bar{r}^{\ast })-x^{\ast }z_{2}{\Theta}^{\ast }E_{t}{\Delta} y_{t+1}\\&&+x^{\ast }m_{2}{\Theta}^{\ast }E_{t}{\Delta} y_{t+1}^{RoW}+x^{\ast }z_{3}{\Theta}^{\ast }E_{t}{\Delta} q_{t+1}+\varepsilon_{t}^{IS^{\ast }} \end{array} $$

(A.7)

Phillips curve:

$$ \pi_{t}^{\ast }=\beta^{\ast }E_{t}\pi_{t+1}^{\ast }+\kappa_{\alpha }^{\ast }(y_{t}^{\ast }-y_{t}^{p\ast })+\frac{\alpha^{\ast }}{1-2\alpha^{\ast }}(\beta^{\ast }E_{t}{\Delta} q_{t+1}-{\Delta} q_{t})+\varepsilon_{t}^{PP^{\ast }} $$

(A.8)

Taylor rule:

$$ R_{t}^{\ast }=\rho^{\ast }R_{t-1}^{\ast }+(1-\rho^{\ast })[\phi_{\pi }^{\ast }\pi_{t}^{\ast }+\phi_{y}^{\ast }(y_{t}^{\ast }-y_{t}^{p\ast })]-\phi_{q}^{\ast }(q_{t}-q_{t}^{ss})+\varepsilon_{t}^{R^{\ast }} $$

(A.9)

Productivity:

$$ y_{t}^{p\ast }-y_{t-1}^{p\ast }={\Gamma}^{y^{p}\ast }+\delta^{\ast }(y_{t-1}^{p\ast }-y_{t-2}^{p\ast })+\varepsilon_{t}^{yp\ast } $$

(A.10)

EA import from US:

$$ im_{US,t}^{EU}=\mu^{\ast }y_{t}^{\ast }+\psi^{\ast }q_{t} $$

(A.11)

EA import from RoW:

$$ im_{W,t}^{EU}=\nu^{\ast }y_{t}^{\ast } $$

(A.12)

• Rest of the world

World trade balance:

$$ {\Xi} im_{W,t}^{US}+(1-{\Xi} )im_{W,t}^{EU}=\digamma ex_{W,t}^{US}+(1-\digamma )ex_{W,t}^{EU} $$

(A.13)

World output:

$$ y_{t}^{RoW}={\Xi} im_{W,t}^{US}+(1-{\Xi} )im_{W,t}^{EU} $$

(A.14)

World’s relative demand for US and EU products:

$$ ex_{W,t}^{US}=ex_{W,t}^{EU}+\psi^{RoW}q_{t} $$

(A.15)

• Real exchange rate determination

  • UIP variant:

    $$ E_{t}q_{t+1}-q_{t}=(R_{t}-E_{t}\pi_{t+1})-(R_{t}^{\ast }-E_{t}\pi_{t+1}^{\ast }) $$

    (A.16)

  • Risk-pooling variant:

    $$ \sigma (c_{t}-c_{t}^{\ast })=q_{t}-v_{t} $$

    (A.17)

    c_t and $c_{t}^{\ast }$ are derived from outputs and net exports using the market-clearing equations.

• Real exchange rate in the steady state⁴:

  $$ q_{t}^{ss} = \frac{n_{1}\mu +n_{2}\nu -m_{2}{\Xi} \nu }{n_{1}\psi + m_{1}\psi^{\ast } + m_{2}(1 - \digamma )\psi^{RoW}}{y_{t}^{p}}-\frac{m_{1}\mu^{\ast }+m_{2}(1-{\Xi} )\nu^{\ast }}{n_{1}\psi + m_{1}\psi^{\ast } + m_{2}(1 - \digamma )\psi^{RoW}}y_{t}^{p\ast } $$

  (A.18)

• All shocks in the model are assumed to follow an AR(1) process.