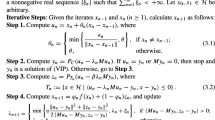Skip to main content
SpringerLink
Log in

Two subgradient extragradient methods based on the golden ratio technique for solving variational inequality problems

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

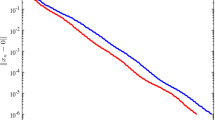
We propose and study two new methods based on the golden ratio technique for approximating solutions to variational inequality problems in Hilbert space. The first method combines the golden ratio technique with the subgradient extragradient method. In the second method, we incorporate the alternating golden ratio technique into the subgradient extragradient method. Both methods use self-adaptive step sizes which are allowed to increase during the execution of the algorithms, thus limiting the dependence of our methods on the starting point of the scaling parameter. We prove that under appropriate conditions, the resulting methods converge either weakly or R-linearly to a solution of the variational inequality problem associated with a pseudomonotone operator. In order to show the numerical advantage of our methods, we first present the results of several pertinent numerical experiments and then compare the performance of our proposed methods with that of some existing methods which can be found in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Availability of data and materials

Not applicable

References

  1. López Acedo, G., Xu, H.K.: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Anal. 67, 2258–2271 (2007)

    Article  MathSciNet  Google Scholar 

  2. Cai, X.J., Gu, G.Y., He, B.S.: On the O(1/t) convergence rate of the projection and contraction methods for variational inequalities with Lipschitz continuous monotone operators. Comput. Optim. Appl. 57, 339–363 (2014)

    Article  MathSciNet  Google Scholar 

  3. Chang, X.K., Yang, J.F.: A golden ratio primal-dual algorithm for structured convex optimization. J. Sci. Comput. 87, 47 (2021). https://doi.org/10.1007/s10915-021-01452-9

    Article  MathSciNet  Google Scholar 

  4. Chang, X.K., Yang, J.F., Zhang, H.C.: Golden ratio primal-dual algorithm with linesearch. SIAM J. Optim. 32, 1584–1613 (2022)

    Article  MathSciNet  Google Scholar 

  5. Censor, Y., Gibali, A., Reich, S.: Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space. Optimization 61, 1119–1132 (2012)

    Article  MathSciNet  Google Scholar 

  6. Censor, Y., Gibali, A., Reich, S.: Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim. Methods Softw. 26, 827–845 (2011)

    Article  MathSciNet  Google Scholar 

  7. Cottle, R.W., Yao, J.C.: Pseudo-monotone complementarity problems in Hilbert space. J. Optim. Theory Appl. 75, 281–295 (1992)

    Article  MathSciNet  Google Scholar 

  8. Dafermos, S.: Traffic equilibrium and variational inequalities. Transp. Sci. 14, 42–54 (1980)

    Article  MathSciNet  Google Scholar 

  9. Facchinei, F., Pang, J.S.: Finite-dimensional variational inequalities and complementarity problems, Volume I and Volume II, SpringerVerlag, New York, NY, USA (2003)

  10. Fichera, G.: Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 8(34), 138–142 (1963)

  11. Gibali, A.: A new Bregman projection method for solving variational inequalities in Hilbert spaces. Pure Appl. Funct. Anal. 3(3), 403–415 (2018)

    MathSciNet  Google Scholar 

  12. Goebel, K., Reich, S.: Uniform convexity, hyperbolic geometry, and nonexpansive mappings. Marcel Dekker, New York (1984)

    Google Scholar 

  13. Goldstein, A.A.: Convex programming in Hilbert space. Bull. Am. Math. Soc. 70, 709–710 (1964)

    Article  MathSciNet  Google Scholar 

  14. Harker, P.T., Pang, J.S.: Finite-dimensional variational inequality and nonlinear complementarity problems: a survey of theory, algorithms and applications. Math. Program. 48, 161–220 (1990)

    Article  MathSciNet  Google Scholar 

  15. He, B.S.: A class of projection and contraction methods for monotone variational inequalities. Appl. Math. Optim. 35, 69–76 (1997)

    Article  MathSciNet  Google Scholar 

  16. Hu, X., Wang, J.: Solving pseudo-monotone variational inequalities and pseudo-convex optimization problems using the projection neural network. IEEE Trans. Neural Netw. 17, 1487–1499 (2006)

    Article  Google Scholar 

  17. Jolaoso, L.O., Oyewole, O.K., Aremu, K.O.: A Bregman subgradient extragradient method with self-adaptive technique for solving variational inequalities in reflexive Banach spaces. Optimization, 1–26 (2021)

  18. Khanh, P.Q., Thong, D.V., Vinh, N.T.: Versions of the subgradient extragradient method for pseudomonotone variational inequalities. Acta Appl. Math. 170, 319–345 (2020)

    Article  MathSciNet  Google Scholar 

  19. Kinderlehrer, D., Stampacchia, G.: An introduction to variational inequalities and their applications. Academic Press, New York-London (1980)

    Google Scholar 

  20. Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Ekon. Mate. Metody. 12, 747–756 (1976)

    MathSciNet  Google Scholar 

  21. Levitin, E.S., Polyak, B.T.: Constrained minimization problems. USSR Comp. Math. Math. Phy. 6, 1–50 (1966)

    Article  Google Scholar 

  22. Malitsky, Y.: Golden ratio algorithms for variational inequalities. Math. Program. 184, 383–410 (2018)

    Article  MathSciNet  Google Scholar 

  23. Mu, Z., Peng, Y.: A note on the inertial proximal point method. Stat. Optim. Inf. Comput. 3(3), 241–248 (2015)

    Article  MathSciNet  Google Scholar 

  24. Nesterov, Y.: A method for solving the convex programming problem with convergence rate O(1/\(k^2\)). Dokl. Akad. Nauk SSSR. 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  25. Ortega, J.M., Rheinboldt, W.C.: Iterative solution of nonlinear equations in several variables. Academic Press, New York (1970)

    Google Scholar 

  26. Osilike, M.O., Aniagbosor, S.C.: Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Math. Comput. Modell. 32, 1181–1191 (2000)

    Article  MathSciNet  Google Scholar 

  27. Oyewole, O.K., Abass, H.A., Mebawondu, A.A., Aremu, K.O.: A Tseng extragradient method for solving variational inequality problems in Banach spaces. Numer. Algorithms 89(2), 769–789 (2002)

    Article  MathSciNet  Google Scholar 

  28. Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys 4, 1–17 (1964)

    Article  Google Scholar 

  29. Shehu, Y., Dong, Q.L., Liu, L.L.: Fast alternated inertial projection algorithms for pseudo-monotone variational inequalities. J. Comput. Appl. Math. 415, 114517 (2022)

    Article  MathSciNet  Google Scholar 

  30. Shehu, Y., Iyiola, O.S.: Projection methods with alternating inertial steps for variational inequalities: weak and linear convergence. Appl. Numer. Math. 157, 315–337 (2020)

    Article  MathSciNet  Google Scholar 

  31. Shehu, Y., Dong, Q.L., Jiang, D.: Single projection method for pseudo-monotone variational inequality in Hilbert spaces. Optimization. 68(1), 385–409 (2019)

    Article  MathSciNet  Google Scholar 

  32. Stampacchia, G.: Formes bilineaires coercitives sur les ensembles convexes. C. R. Acad. Sci. 258, 4413–4416 (1964)

    MathSciNet  Google Scholar 

  33. Sun, D.: A class of iterative methods for solving nonlinear projection equations. J. Optim. Theory Appl. 91, 123–140 (1996)

    Article  MathSciNet  Google Scholar 

  34. Thong, D.V., Yuang, J., Chol, Y.J., Rassias, T.M.: Explicit extragradient-like method with adaptive stepsizes for pseudomonotone variational inequalities. Optim. Lett. 15, 2181–2199 (2021)

    Article  MathSciNet  Google Scholar 

  35. Zhang, C., Chu, Z.: New extrapolation projection contraction algorithms based on the golden ratio for pseudo-monotone variational inequalities. AIM Mathematics. 8(10), 23291–23312 (2023)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Both authors appreciate with thanks the efforts of the referees for their careful reading, helpful comments, and important suggestions, which have helped improve the quality of the manuscript.

Funding

Simeon Reich was partially supported by the Israel Science Foundation (grant no. 820/17), by the Fund for the Promotion of Research at the Technion (grant 2001893), and by the Technion General Research Fund (grant 2016723).

Author information

Authors and Affiliations

  1. Department of Mathematics, The Technion – Israel Institute of Technology, 32000, Haifa, Israel

    Olawale K. Oyewole & Simeon Reich

Authors
  1. Olawale K. Oyewole
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Simeon Reich
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Both authors worked equally on the results and approved the final manuscript.

Corresponding author

Correspondence to Olawale K. Oyewole.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Oyewole, O.K., Reich, S. Two subgradient extragradient methods based on the golden ratio technique for solving variational inequality problems. Numer Algor (2024). https://doi.org/10.1007/s11075-023-01746-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11075-023-01746-z

Keywords

Mathematics Subject Classification (2010)

Search

Navigation