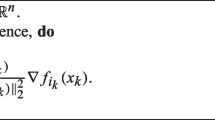Nullspaces yield new explicit Runge–Kutta pairs

Abstract

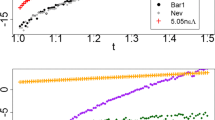
Sixty years ago, Butcher (Butcher Math. Soc. 3, 185–201 1963) characterized a natural tabulation of the order conditions for Runge–Kutta methods of order p as an isomorphism from the set of rooted trees having up to p nodes and provided examples of explicit and implicit methods of several orders. Within a few years, Fehlberg (Fehlberg 1968) derived pairs of explicit methods of successive orders that could be implemented efficiently by using the difference of each pair of estimates to control the local error. Unfortunately, Fehlberg’s pairs were deficient for quadrature problems. Subsequently, this author (Verner SIAM J. Numer. Anal. 15, 772–790 1978, Verner SIAM J. Numer. Anal. 16, 857–875 1979) derived parametric families of explicit Runge–Kutta pairs of increasing orders 6 to 9 that avoided this problem altogether. These, and most known explicit methods, have been derived by exploiting certain “simplifying conditions” suggested by Butcher (Butcher Math. Soc. 3, 185–201 1963, Butcher 1987 [pp. 194 f.]) that imposed constraints on subsets of the coefficients and thereby simplified the solution of the order conditions for moderate to high-order methods. “RK-Test-21”, a MAPLE program developed recently by Butcher (Butcher 2021), was applied to derive known 13-stage pairs of orders 7 and 8. Unexpectedly, results of this application revealed the existence of some previously unknown pairs—i.e., some with the correct orders that satisfied most, but not all, of the previously known simplifying conditions. This present study develops formulas for directly computing exact coefficients of these new pairs together with others lying within this new parametric family of (13,7-8) pairs. While the best of these new pairs falls short of the best of pairs already known, the properties discovered might be utilized to precisely characterize recently reported higher-order methods found using other approaches by Khashin (Khashin 2009) and Zhang (Zhang 2019) and possibly lead to finding other Runge–Kutta and related yet unknown methods.

Appendices

Appendix

This appendix displays an example of a new nullspace (13,7-8) explicit Runge–Kutta pair. The final line in Table 4 states the properties of a near-optimal new pair found. For that pair, the nodes are ${{\textbf {c}}}= {\{0,1/1000,1/9,1/6},5/12,1/2,5/6,$ ${1/6,2/3,19/25,21/25,1,1\}}$, $a_{7,6}=7/3,$ and $a_{8,7}=5/267$. Here, we report a nearby method that has $LTE_2=10^{-5}$, $D=70.386$ and interval of absolute stability of the method of order eight equal to $(-4.567,0]$. To represent this pair, we first state the pair for which $a_{7,6}=a_{8,7}=0$ in Table 5.

Table 5 A nullspace (13,7-8) pair for which the main stage order is three

A different pair arises for almost every choice of $a_{7,6}$ and $a_{8,7}$ although a few discrete choices fail to yield a pair as a result of singularities occurring on the application of the algorithm to derive nullspace pairs. For nodes in Table 5, and almost any choice of $a_{7,6},\ a_{8,7}$, a more general pair is obtained by computing the matrix $\mathbf {\widehat{A}}$ using the following vectors in formula (17):

• Column $C1=[0,0,0,0,0,0,1,-\frac{1}{6},-\frac{343}{243},-\frac{2058}{3125},\frac{343}{1944},\frac{5831}{240},\frac{686}{195}]$

• Row $R1=[-\frac{2}{5},0,0,1,-\frac{8}{5},1,0,0,0,0,0,0,0]$

• Column $C2=[0,0,0,0,0,0,0,1,\frac{2744}{1215},\frac{24696}{78125},-\frac{343}{9720},\frac{5831}{200},\frac{1372}{325}]$

• Row $R2=[\frac{1073}{343},0,0,-\frac{3330}{343},\frac{8352}{343},-\frac{6438}{343},1,0,0,0,0,0,0]$

For a nearly optimal pair with these nodes, choose $a_{7,6}=27/10,\ a_{8,7}=1/72$ in formula (17).

An optimal pair

In contrast to the previous pair, the nodes may be changed to optimize the pair—in the sense that the 2-norm of the local truncation error coefficient discrepancies of the higher-order method is minimized. The final line in Table 4 states the properties of this pair. Slight improvements on this pair are possible by reducing $c_2$ towards zero, but such improvements are marginal. Table 6 records coefficients of $\{{\textbf {b}},\ \varvec{\widehat{b}},\ {\textbf {A}},\ {\textbf {c}} \}$ when $a_{7,6}=0$ and $a_{8,7}=0$ for the optimal pair.

Table 6 A basic nullspace (13,7-8) pair for optimality with main stage order three

A more general pair is obtained when matrix $\mathbf {\widehat{A}}$ is computed with almost any values of $a_{7,6}$ and $a_{8,7}$ using the four following vectors in (17):

• Column $C1=[0,0,0,0,0,0,1,-\frac{1}{5},-8,-\frac{13844844}{1953125},\frac{4279716}{1953125},-\frac{54108}{2315},\frac{3564}{1105}]$

• Row $R1=[-\frac{2}{5},0,0,1,-\frac{8}{5},1,0,0,0,0,0,0,0]$

• Column $C2=[0,0,0,0,0,0,0,1,10,\frac{38073321}{9765625},\frac{1069929}{9765625},-\frac{13527}{463},\frac{891}{221}]$

• Row $R2=[\frac{8}{3},0,0,-\frac{25}{3},\frac{64}{3},-\frac{50}{3},1,0,0,0,0,0,0]$

In particular, we get a nearly optimal pair for the choices of $a_{7,6}=7/3$ and $a_{8,7}=5/267$ using these vectors in (17).