1 Introduction

Let \(\,F:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\,\) be a nonlinear continuously differentiable function, we are interested in solving the problem

$$\begin{aligned} F(\varvec{x})=0, \end{aligned}$$
(1)

especially when \(\,n\,\) is considerably large.

The most popular method for solving (1) is the Newton method [1, 2]. This method has very good convergence properties, but its greatest difficulty is having to calculate the Jacobian matrix of \(\,F, F',\,\) and evaluate it in each iteration which is, computationally, very expensive. One strategy to avoid this calculus and the evaluations is to use an approximation to \(\,F'(\varvec{x})\,\) which entails to a variety of methods known as quasi-Newton methods [3,4,5,6,7,8].

However, both Newton and quasi-Newton methods need to solve a linear system of equations in their routines; thus, if \(\,n\,\) is large, even quasi-Newton methods are expensive. It is important to say that although many quasi-Newton methods admit a cheap formula for updating the inverse of \(\,B_k,\,\) generally these formulas depend on a term that involves a fraction whose denominator could be zero or a very small quantity so in practice this could lead to an ill-conditioned matrix. To counter this, iterative Krylov methods [9,10,11] were introduced to Newtonian algorithms, which contributed to decrease the computational cost on these algorithms. This strategy consists of finding approximately the search direction, so the mentioned linear system will solve with some tolerable error.

For Newton-Krylov methods, fast convergence properties have been proved whereas, for quasi-Newton-Krylov methods, have been proved fast convergence properties if the Krylov method is the conjugate gradient method [12,13,14,15] or employed a Jacobian restart strategy [16]. The greatest difficulty of inexact quasi-Newton methods is that so far it has not been possible to prove that inexact quasi-Newton direction are descent directions for the associated merit function to (1).

Several studies are concerned with solving (1). In [17, 18], the authors proposed a different approach to solve (1). They proposed a nonmonotone spectral free derivative method. This was an ingenious proposal based on spectral gradient method and systematically uses \(\,\pm F(\varvec{x}_k)\,\) as a search direction. Due to the simplicity of this method, the computational cost is very low and although global convergence has been proved, linear or superlinear convergence has not yet been proved.

In this paper, we establish a global inexact quasi-Newton method, which is of low computational cost to solve (1). We propose a two-stage linear search procedure for obtaining descent direction and we ensure the global convergence without falling into infinite cycles. Also, under reasonable conditions, we prove fast convergence properties for the method.

This paper is organized as follows. In Section 2 we introduce the new algorithm and make some remarks. In Section 3 we develop the convergence theory of the algorithm introduced previously. Besides, we prove global convergence of the method and the linear and superlinear convergence rate. In Section 4 we present some numerical experiments that show the robustness and competitiveness of the new algorithm. Furthermore, we compare the performance of our algorithm with respect to the algorithms proposed in [17, 18]. Finally, we make some remarks in Section 5.

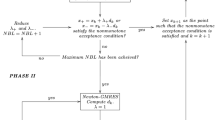
2 Algorithm

In this section, we describe the inexact free derivative quasi-Newton method (IFDQ) that we propose in this work.

Taking into account that one of our interests is to purpose a global algorithm to solve (1), we considered the following minimization problem to this.

$$\begin{aligned} \text {minimize}&\,\,f(\varvec{x})\\ \varvec{x}\in {\mathbb {R}}^{n} \nonumber \end{aligned}$$
(2)

where \(\,f(\varvec{x})=\frac{1}{2}\Vert F(\varvec{x})\Vert ^2\,\) is the associated merit function to (1) and \(\,\Vert \cdot \Vert \,\) is the Euclidean norm in \(\,{\mathbb {R}}^{n}.\,\)

Below we show the IFDQ algorithm which main innovation is the two-stage linear search procedure

Algorithm 1
figure a

IFDQ.

Full size image

Remark 1

So far it has not been possible to prove, in general, that the inexact quasi-Newton direction, obtained in Step 1 is a descent direction for the merit function \(\,f\,\) given in (2). For this reason, it is necessary to try both \(\,{\varvec{d}}_k\,\) and \(\,-{\varvec{d}}_k\,\) directions in the line search procedure.

Remark 2

In Step 2 we set two trial directions, \(\varvec{d}_k\) and \(-\varvec{d}_k\). Note that unless \(\nabla f^{T}\varvec{d}_k=0,\) at least one of the trial directions will be a descent direction, hence, the two-stage linear search procedure will not fall in an infinite cycle.

Remark 3

In the linear search procedure we seek a sufficient decrease of the merit function \(\,f\,\) but if the step length \(\,\alpha _k\,\) is too small then the algorithm breaks down, avoiding small steps with a poor decrease. Note that the lower bound for the step length is set by the user and can be as small as desired. So to prevent either, many breaks of the algorithm and small steps with a poor decrease we recommend to take \(\lambda =10^{-4}.\) Whit this value, the algorithm showed a good performance.

3 Convergence theory

In this section, we present the main theoretical results obtained for IFDQ algorithm. In the following lemmas and theorems we show that, under reasonable assumptions, the algorithm converges to a solution of the problem (1) and locally enjoys good convergence properties: full inexact quasi-Newton step is accepted and it can even has until superlinear converge.

The hypotheses under which we develop the convergence theory of the proposed algorithm are:

  1. H1.

    There exist \(\,\textbf{x}^*\in {\mathbb {R}}^{n}\,\) such that \(\,F(\textbf{x}^*)=0.\,\)

  2. H2.

    There exists \(\,T>0\,\) such that \(\,\Vert B_k^{-1}\Vert <T\,\) for all \(\,k\ge 0.\,\)

  3. H3.

    \(\,F'(\varvec{x})\,\) is a Lipschitz function, i.e., there exist \(\,L>0\,\) such that

    $$\begin{aligned} \Vert F^{\prime }(\varvec{x})-F^{\prime }({\varvec{y}})\Vert \le L\Vert \varvec{x}-{\varvec{y}}\Vert \quad \forall \varvec{x},{\varvec{y}}\in {\mathbb {R}}^{n}. \end{aligned}$$
  4. H4.

    \(\{B_k\}\) is a sequence such that

    $$\begin{aligned} \underset{k\rightarrow \infty }{\textrm{lim}}\frac{\Vert (B_{k}-F^{\prime }(\varvec{x}_k)){\varvec{d}}_k\Vert }{\Vert {\varvec{d}}_k\Vert }=0. \end{aligned}$$
    (4)

Previous hypotheses are classical hypotheses for quasi-Newton methods. Hypotheses H1 and H3 depend on the problem to be solved whereas H2 and H4 depends on the approximations to \(F^{\prime }(\varvec{x}_{k}).\)

An immediate consequence of H3 is that for all \(\,\varvec{x},\,{\varvec{y}}\in {\mathbb {R}}^{n},\,\)

$$\begin{aligned} \Vert F(\varvec{x})-F({\varvec{y}})-F'({\varvec{y}})(\varvec{x}-{\varvec{y}})\Vert \le \frac{L}{2}\Vert \varvec{x}-{\varvec{y}}\Vert ^2. \end{aligned}$$
(5)

It is important to mention that (4) in H4 is known as Dennis-Moré condition.

The first lemma of our theoretical development ensures that if the IFDQ algorithm does not break down then, it generates a sequence such that its images converge to zero.

Lemma 1

If \(\{\varvec{x}_k\}\) is a sequence generated by IFDQ algorithm then \(\underset{k \rightarrow \infty }{\textrm{lim}}\left\Vert {F}(\varvec{x}_k)\right\Vert =0\).

Proof

Let \(\{\varvec{x}_k\}\) be a sequence given by IFDQ algorithm, it follows that

$$\begin{aligned} \left\Vert {F}({\varvec{x}}_{k+1})\right\Vert\le & {} (1-\alpha _k\lambda )\left\Vert {F}({\varvec{x}}_k)\right\Vert \\\le & {} (1-\lambda ^2)\left\Vert {F}(\varvec{x}_k)\right\Vert \\\le & {} (1-\lambda ^2)^{k+1}\left\Vert {F}(\varvec{x}_0)\right\Vert . \end{aligned}$$

By recalling that \(1-\lambda ^2<1,\) the result is established. \(\square \)

The next result is immediate since \(\,F\,\) is a continuous function.

Corollary 1

If \(\{\varvec{x}_k\}\) is a sequence generated by IFDQ algorithm and \(\varvec{x}^{*}\) is a cluster point of \(\{\varvec{x}_k\}\) then \(\varvec{x}^{*}\) is a solution of (1).

The following theorem ensures the convergence of the sequence generated by IFDQ algorithm under the assumption of non-singularity of the Jacobian matrix \(\,F'\,\) in the solution of the problem.

Theorem 1

Assume H2. Let \(\{\varvec{x}_k\}\) be a sequence generated by IFDQ algorithm. If \(\varvec{x}^{*}\in {\mathbb {R}}^{n}\) is a cluster point of \(\{\varvec{x}_k\}\) such that \(F'(\varvec{x}^{*})\) is nonsingular then \(F(\varvec{x}^{*})=0\) and \(\underset{k \rightarrow \infty }{\textrm{lim}}\varvec{x}_k=\varvec{x}^{*}\).

Proof

Let \(\{\varvec{x}_{k_{j}}\}\) be a subsequence of \(\{\varvec{x}_k\}\) such that \(\varvec{x}_{k_{j}}\rightarrow \varvec{x}^{*}\) as \(k_{j}\rightarrow \infty \). By recalling that F is a continuous function and Lemma 1, we have that \(F(\varvec{x}^{*})=0\).

On the other hand, let \(K=\left\Vert {F}'(\varvec{x}^{*})^{-1}\right\Vert \) and \(\delta >0\) small enough such that for any \({\varvec{y}}\in B(\varvec{x}^{*},\delta )\) we have that

  1. i

    \(\,F'({\varvec{y}})^{-1}\,\) there exists.

  2. ii

    \(\,\left\Vert {F}'({\varvec{y}})^{-1}\right\Vert <2K.\,\)

  3. iii

    \(\left\Vert {F}({\varvec{y}})-F(\varvec{x}^*)-F'(\varvec{x}^{*})({\varvec{y}}-\varvec{x}^{*})\right\Vert \le \frac{1}{2K}\left\Vert {\varvec{y}}-\varvec{x}^{*}\right\Vert .\,\)

The existence of \(\,\delta \,\) can be guaranteed thanks to Lemmas 1.1 and 1.2 in [15]. Observe that if \({\varvec{y}}\in B(\varvec{x}^{*},\delta )\) then

$$\begin{aligned} \Vert F(\varvec{y})\Vert= & {} \Vert F'(\varvec{x}^*)(\varvec{y}-\varvec{x}^*)+F(\varvec{y})-F(\varvec{x}^*)-F'(\varvec{x}^*)(\varvec{y}-\varvec{x}^*)\Vert \\\ge & {} \Vert F'(\varvec{x}^*)({\varvec{y}}-\varvec{x}^*)\Vert -\Vert F({\varvec{y}})-F(\varvec{x}^*)-F'(\varvec{x}^*)({\varvec{y}}-\varvec{x}^*)\Vert \\\ge & {} \Vert F'(\varvec{x}^*)({\varvec{y}}-\varvec{x}^*)\Vert -\frac{1}{2K}\Vert {\varvec{y}}-\varvec{x}^*\Vert \end{aligned}$$

and

$$\begin{aligned} \left\Vert \varvec{y}-\varvec{x}^{*}\right\Vert =\left\Vert {F}'(\varvec{x}^{*})^{-1}F'(\varvec{x}^*)({\varvec{y}}-\varvec{x}^{*})\right\Vert \le K\left\Vert {F}'(\varvec{x}^{*})({\varvec{y}}-\varvec{x}^{*})\right\Vert . \end{aligned}$$

By combining the two last inequalities we can infer that

$$\begin{aligned} \left\Vert \varvec{y}-\varvec{x}^{*}\right\Vert \le 2K\left\Vert {F}({\varvec{y}})\right\Vert ,\quad \forall {\varvec{y}}\in B(\varvec{x}^{*},\delta ). \end{aligned}$$
(6)

On the other hand, let \(\,\epsilon \in (0,\delta /4).\,\) Since \(\varvec{x}^{*}\) is a cluster point of \(\{\varvec{x}_{k}\}\) and \(F(\varvec{x}^{*})=0\) then, there exist \(\,k\,\) large enough such that

$$\begin{aligned} \varvec{x}_{k}\in S_{\epsilon }:= \left\{ {\varvec{y}}\in \mathbb {R}^n: {\varvec{y}}\in B(\varvec{x}^{*},\delta /2),\,\,\, M(1+\theta )\left\Vert {F}({\varvec{y}})\right\Vert <\epsilon \right\} , \end{aligned}$$

where \(\,M=\max \{K,T\}\,\) and \(\,T\,\) is the constant of hypothesis H2. Hence, we obtain

$$\begin{aligned} \left\Vert \varvec{d}_k\right\Vert= & {} \left\Vert {B}_k^{-1}[-F(\varvec{x}_k)+F(\varvec{x}_k)+B_{k}{\varvec{d}}_k]\right\Vert \nonumber \\\le & {} \left\Vert {B}_k^{-1}\right\Vert \left( \left\Vert {F}(\varvec{x}_k)\right\Vert +\left\Vert {F}(\varvec{x}_k)+B_{k}{\varvec{d}}_k\right\Vert \right) \nonumber \\\le & {} T \left( \left\Vert {F}(\varvec{x}_k)\right\Vert +\theta _k\left\Vert {F}(\varvec{x}_k)\right\Vert \right) \nonumber \\\le & {} T(1+\theta _k)\left\Vert {F}(\varvec{x}_k)\right\Vert \\< & {} M (1+\theta _k) \left\Vert {F}(\varvec{x}_k)\right\Vert .\nonumber \end{aligned}$$
(7)

Now, since \(\varvec{x}_k\in S_{\epsilon }\) then \(\left\Vert \varvec{d}_{k}\right\Vert <\epsilon \). Moreover, we have that

$$\begin{aligned} \left\Vert {\varvec{x}}_{k+1}-\varvec{x}^{*}\right\Vert= & {} \left\Vert {\varvec{x}}_k+\alpha _k{\varvec{d}}_k-\varvec{x}^{*}\right\Vert \\\le & {} \left\Vert \varvec{x}_{k}-\varvec{x}^{*}\right\Vert +\vert \alpha _k \vert \left\Vert \varvec{d}_k\right\Vert \\< & {} \delta . \end{aligned}$$

Thus, we conclude \(\varvec{x}_{k+1}\in B(\varvec{x}^{*},\delta )\). On the other hand, since IFDQ attempts for a monotone decrease and \(\,\varvec{x}_k\in S_{\varepsilon }\,\) then

$$\begin{aligned} \left\Vert {F}(\varvec{x}_{k+1})\right\Vert \le \left\Vert {F}(\varvec{x}_{k})\right\Vert \le \frac{\epsilon }{M(1+\theta )}. \end{aligned}$$
(8)

So, from (6) and using the last inequality we can infer that

$$\begin{aligned} \left\Vert \varvec{x}_{k+1}-\varvec{x}^{*}\right\Vert\le & {} \frac{2K\epsilon }{M(1+\theta )}\nonumber \\\le & {} \frac{2\epsilon }{(1+\theta )}\\\le & {} {2\epsilon }.\nonumber \end{aligned}$$
(9)

Finally, from (8) and (9) we have that \(\varvec{x}_{k+1}\in S_{\epsilon },\) with which we prove that \(\,\varvec{x}_k\in S_{\epsilon }\,\) for all \(\,k\,\) large enough, and since \(\,\Vert F(\varvec{x}_k)\Vert \rightarrow 0\,\) then, from (6), \(\,\varvec{x}_k\rightarrow \varvec{x}^*\,\) as \(\,k\rightarrow \infty .\,\) \(\square \)

In the next lemma, we show that the trial directions in Step 1 remain bounded for all \(\,k.\,\)

Lemma 2

Assume H2. Let \(\{\varvec{x}_k\}\) be a sequence generated by IFDQ algorithm then, \(\left\Vert \varvec{d}_{k}\right\Vert \le 2T \left\Vert {F}(\varvec{x}_{k})\right\Vert \) and \(\underset{k\rightarrow \infty }{\textrm{lim}}\left\Vert \varvec{x}_{k+1}-\varvec{x}_{k}\right\Vert =0\).

Proof

The first part of this lemma follows from (7) and the fact that \(\,\theta _k\in (0,\,1).\,\)

On the other side, observe that

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}_k\Vert= & {} \Vert \varvec{x}_k+\alpha _k{\varvec{d}}_k-\varvec{x}_k\Vert \\= & {} \alpha _k\Vert {\varvec{d}}_k\Vert \\\le & {} 2T\Vert F(\varvec{x}_k)\Vert . \end{aligned}$$

Thus, by Lemma 1 and the last inequality, we have the desired result. \(\square \)

The next theorem ensures convergence of the sequence generated by IFDQ algorithm without non-singularity condition of \(\,F'(\varvec{x}^*).\,\)

Theorem 2

Let \(\{\varvec{x}_{k}\}\) be a sequence generated by the algorithm. If \(\varvec{x}^{*}\) is an isolated cluster point of the sequence then, \(\underset{k\rightarrow \infty }{\textrm{lim}}\varvec{x}_{k}=\varvec{x}^{*}\).

Proof

Taking into account Lemmas 1 and 2, this proof follows the same ideas of the proof of theorem 3 in [18] \(\square \)

The next theorem ensures that, at least locally, the IFDQ algorithm shows good performance in the sense that the full quasi-Newton step will be accepted in the two-stage linear search procedure. In the proof we assume a weaker hypothesis than the Dennis-Moré condition. This hypothesis is related with the bounded deterioration property and ensures that at least, for all k large enough, the approximation \(B_k\) to the jacobian matrix \(F'(\varvec{x}_k)\) is bounded above by a constant.

As in the proof of Theorem 1, let \(\,M=\max \{K,T\}\,\) where \(\,T\,\) is the constant in H2.

Theorem 3

Assume hypotheses H1, H2 and H3. Let \(\,\{\varvec{x}_k\}\,\) be a sequence generated by IFDQ algorithm and \(\,\varvec{x}^*\,\) be a cluster point of the sequence. If \(\,F'(\varvec{x}^*)\,\) is nonsingular and for all \(\,k\,\) large enough \(\,\theta _k<\frac{1}{3}-\lambda \,\) and \(\Vert F'(\varvec{x}_k)-B_k\Vert <\frac{1}{24M^3}\) then \(\,\varvec{d}_k\,\) and \(\,\alpha _k=1\,\) will be accepted, in the two-stage linear search procedure.

Proof

Observe that

$$\begin{aligned} F(\varvec{x}_k+{\varvec{d}}_k)= & {} F(\varvec{x}_k)+\int _0^1F'(\varvec{x}_k+t{\varvec{d}}_k){\varvec{d}}_k\, dt\\= & {} F(\varvec{x}_k)+F'(\varvec{x}_k){\varvec{d}}_k+B_k{\varvec{d}}_k-B_k{\varvec{d}}_k\\{} & {} +\int _0^1\left[ F'(\varvec{x}_k+t{\varvec{d}}_k){\varvec{d}}_k- F'(\varvec{x}_k){\varvec{d}}_k\right] dt. \end{aligned}$$

Thus,

$$\begin{aligned} \left\Vert {F}(\varvec{x}_k+{\varvec{d}}_k)\right\Vert\le & {} \left\Vert {F}(\varvec{x}_k)+B_k{\varvec{d}}_k\right\Vert +\left\Vert (F'(\varvec{x}_k)-B_k){\varvec{d}}_k\right\Vert \\{} & {} +\int _0^1\left\Vert {F}'(\varvec{x}_k+t{\varvec{d}}_k)-F'(\varvec{x}_k)\right\Vert \left\Vert \varvec{d}_k\right\Vert {dt}\\\le & {} \theta _k\left\Vert {F}(\varvec{x}_k)\right\Vert +\left\Vert {F}'(\varvec{x}_k)-B_k\right\Vert \left\Vert \varvec{d}_k\right\Vert +\int _0^1 L\left\Vert {t}\varvec{d}_k\right\Vert \left\Vert \varvec{d}_k\right\Vert {dt}\\ \end{aligned}$$

so, from Lemma 2 and taking into account that for all \(\,k\,\) large enough

$$\begin{aligned} \Vert F'(\varvec{x}_k)-B_k\Vert<\frac{1}{24M^3}<\frac{1}{6T} \end{aligned}$$

we have that

$$\begin{aligned} \left\Vert {F}(\varvec{x}_k+{\varvec{d}}_k)\right\Vert\le & {} \theta _k\left\Vert {F}(\varvec{x}_k)\right\Vert +\frac{1}{3}\left\Vert {F}(\varvec{x}_k)\right\Vert +\frac{L}{2}\left\Vert \varvec{d}_k\right\Vert ^2\nonumber \\\le & {} \theta _k\left\Vert {F}(\varvec{x}_k)\right\Vert +\frac{1}{3}\left\Vert {F}(\varvec{x}_k)\right\Vert +2T^2L\left\Vert {F}(\varvec{x}_k)\right\Vert ^2\nonumber \\= & {} \left( \theta _k+\frac{1}{3}+2T^2L\left\Vert {F}(\varvec{x}_k)\right\Vert \right) \left\Vert {F}(\varvec{x}_k)\right\Vert . \end{aligned}$$
(10)

Now, since \(\,\left\Vert {F}(\varvec{x}_k)\right\Vert \,\) converges to zero then, for all \(\,k\,\) large enough

$$\begin{aligned} \Vert F(\varvec{x}_k)\Vert <\frac{1}{6T^2L}. \end{aligned}$$
(11)

Hence, by (10), (11) and since \(\,\theta _k<\frac{1}{3}-\lambda \,\) then, for all k large enough

$$\begin{aligned} \left\Vert {F}(\varvec{x}_k+{\varvec{d}}_k)\right\Vert \le (1-\lambda )\left\Vert {F}(\varvec{x}_k)\right\Vert \end{aligned}$$

thus \(\,\alpha _k=1\,\) and \(\,{\varvec{d}}_k\,\) will be accepted. \(\square \)

The following theorem is the first theorem in which we show good convergence properties of the IFDQ algorithm. For this purpose, we assume that \(\,F'(\varvec{x}^*)\,\) is nonsingular, that \(\,\Vert F'(\varvec{x}^*)^{-1}\Vert =K\,\) and that \(\,M=\max \{K,T\}\,\) where \(\,T\,\) is the constant in H2.

Theorem 4

Under the same hypotheses of the previous theorem. If in addition

$$\begin{aligned} \,\theta _k<\min \left\{ \frac{1}{12M^2},\,\frac{1}{3}-\lambda \right\} \, \end{aligned}$$

then \(\,\varvec{x}_k\rightarrow \varvec{x}^*\,\) linearly.

Proof

By using Theorem 3, we can ensure that the full quasi-Newton step will be accepted for all \(\,k\,\) large enough and by Theorem 1, \(\,\varvec{x}_k\rightarrow \varvec{x}^*\,\), so for all \(\,k\,\) large enough, \(\,F'(\varvec{x}_k)^{-1}\,\) there exist and \(\,\Vert F'(\varvec{x}_k)^{-1}\Vert \le 2M\,\) hence,

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert= & {} \Vert \varvec{x}_k+{\varvec{d}}_k-\varvec{x}^*+F'(\varvec{x}_k)^{-1}F(\varvec{x}_k)-F'(\varvec{x}_k)^{-1}F(\varvec{x}_k)\Vert \\\le & {} \Vert \varvec{x}_k-\varvec{x}^*-F'(\varvec{x}_k)^{-1}F(\varvec{x}_k)\Vert +\Vert F'(\varvec{x}_k)^{-1}(F(\varvec{x}_k)+F'(\varvec{x}_k){\varvec{d}}_k)\Vert \\\le & {} \Vert F'(\varvec{x}_k)^{-1}[F(\varvec{x}^*)-F(\varvec{x}_k)-F'(\varvec{x}_k)(\varvec{x}^*-\varvec{x}_k)]\Vert +\\{} & {} \qquad \Vert F'(\varvec{x}_k)^{-1}\Vert \Vert F(\varvec{x}_k)+F'(\varvec{x}_k){\varvec{d}}_k+B_k{\varvec{d}}_k-B_k{\varvec{d}}_k\Vert \\\le & {} 2M\Vert F(\varvec{x}^*)-F(\varvec{x}_k)-F'(\varvec{x}_k)(\varvec{x}^*-\varvec{x}_k)\Vert +2M[\Vert F(\varvec{x}_k)+B_k{\varvec{d}}_k\Vert \\{} & {} \qquad +\Vert F'(\varvec{x}_k){\varvec{d}}_k-B_k{\varvec{d}}_k\Vert ] \end{aligned}$$

by (5) and Step 1 in the algorithm we have that

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M[\theta _k\Vert F(\varvec{x}_k)\Vert +\Vert F'(\varvec{x}_k)-B_k\Vert \Vert {\varvec{d}}_k\Vert ]. \end{aligned}$$
(12)

Thus, by Lemma 2,

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M\left[ \theta _k+\frac{1}{12M^2}\right] \Vert F(\varvec{x}_k)\Vert \\= & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M\left[ \theta _k+\frac{1}{12M^2}\right] \Vert F(\varvec{x}_k)-F(\varvec{x}^*)\Vert . \end{aligned}$$

So, by the mean value theorem,

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+4M^2\left[ \theta _k+\frac{1}{12M^2}\right] \Vert \varvec{x}_k-\varvec{x}^*\Vert \nonumber \\= & {} \left[ ML\Vert \varvec{x}_k-\varvec{x}^*\Vert +4M^2\left( \theta _k+\frac{1}{12M^2}\right) \right] \Vert \varvec{x}_k-\varvec{x}^*\Vert \end{aligned}$$
(13)

thereby, for \(\,k\,\) large enough such that

$$\begin{aligned} \Vert \varvec{x}_k-\varvec{x}^*\Vert <\frac{1}{3ML}, \end{aligned}$$

since \(\,\theta _k<\frac{1}{12M^2},\,\) we can conclude that

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert <R\Vert \varvec{x}_k-\varvec{x}^*\Vert \end{aligned}$$

where \(\,0<R<1,\,\) which completes the proof. \(\square \)

Finally, to complete our theoretical development, the next theorem ensures, under reasonable assumptions, superlinear convergence of the IFDQ algorithm.

Theorem 5

Assume H1, H2, H3 and H4. Let \(\,\{\varvec{x}_k\}\,\) be a sequence generated by IFDQ algorithm and \(\,\varvec{x}^*\,\) be a cluster point of the sequence. If \(\,F'(\varvec{x}^*)\,\) is nonsingular and \(\,\theta _k\rightarrow 0\,\) then \(\,\varvec{x}_k\rightarrow \varvec{x}^*\,\) superlinearly.

Proof

From (12) we can infer that

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M\left[ \theta _k\Vert F(\varvec{x}_k)\Vert +\frac{\Vert F'(\varvec{x}_k)-B_k\Vert \Vert {\varvec{d}}_k\Vert }{\Vert {\varvec{d}}_k\Vert }\right] . \end{aligned}$$

By Lemma 2 and the Mean Value Theorem,

$$\begin{aligned} \Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M\left[ \theta _k+2M\frac{\Vert F'(\varvec{x}_k)-B_k\Vert }{\Vert {\varvec{d}}_k\Vert }\right] \Vert F(\varvec{x}_k)\Vert \\= & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2\!+\!2M\left[ \theta _k\!+\!2M\frac{\Vert F'(\varvec{x}_k)-B_k\Vert }{\Vert {\varvec{d}}_k\Vert }\right] \Vert F(\varvec{x}_k)-F(\varvec{x}^*)\Vert \\\le & {} ML\Vert \varvec{x}_k-\varvec{x}^*\Vert ^2+2M\left[ \theta _k+2M\frac{\Vert F'(\varvec{x}_k)-B_k\Vert }{\Vert {\varvec{d}}_k\Vert }\right] \Vert \varvec{x}_k-\varvec{x}^*\Vert \\= & {} \left[ ML\Vert \varvec{x}_k-\varvec{x}^*\Vert +2M\left( \theta _k+2M\frac{\Vert F'(\varvec{x}_k)-B_k\Vert }{\Vert {\varvec{d}}_k\Vert }\right) \right] \Vert \varvec{x}_k-\varvec{x}^*\Vert \end{aligned}$$

The desired result follows from hypothesis H4 and the fact that \(\,\varvec{x}_k\rightarrow \varvec{x}^*\,\) and \(\,\theta _k\rightarrow 0\,\) as \(\,k\rightarrow \infty .\,\) \(\square \)

4 Numerical experiments

In this section we report the numerical results of the IFDQ algorithm when solving twenty problems. Sixteen of the problems were taken from [17] and references therein, the rest of the problems were taken from [19,20,21]. It is important to say that we did not take into account problems 13, 14, 15 and 18 of [17]. First, problems 13 and 14 include many random parameters that difficult the reproduction of the experiments. Second, the poor performance of the algorithms with problems 15 and 18 did not allow us to draw relevant conclusions.

The experiments were carried out in Matlab\(^{\circledR }\)   using an Intel \(\text {Core}2^{TM}\) laptop with a RAM of 4GB. To evaluate the performance of the IFDQ algorithm, we ran experiments and compared the results with four more algorithms: SANE [17], DF-SANE [18], Ac-DFSANE [22] and NITSOL [23].

SANE and DF-SANE are spectral free derivative algorithms. The descent trial direction at each iteration of these methods is \(\,\pm F(\varvec{x}_k)\,\) and the main difference between them is the linear search.

Ac-DFSANE is an accelerated version, proposed recently, for the DF-SANE algorithm. This chooses in a very ingenious way the new iterate improving in many times the descent achieved in the linear search.

Finally, NITSOL is a practical and efficient implementation of the classical inexact Newton method with GMRES procedure to find the descent direction. This algorithm approximates derivatives by finite differences when these are not available.

For all algorithms we used \(\,\Vert F(\varvec{x}_k)\Vert <10^{-6}\,\) and \(\,k<300\,\) as stop criteria. For IFDQ algorithm we took \(\,B_0=I_n\,\) as initial approximation to \(\,F'(\varvec{x}_0); \theta _k=\frac{1}{k+2}\,\) as inexact parameter in Step 1 and \(\,\lambda =10^{-4}\,\) and \(\,\beta =0.5\,\) for the two-stage linear search procedure in Step 2. To find \(\,{\varvec{d}}_k\,\) in Step 1, we used GMRES procedure.

In the same way, in Step 3 we used the “good” Broyden update [24]. It is important to say that this update is a least change secant update, thus satisfying the well-known property of bounded deterioration [2, 25] with which Dennis and Schnabel in [2] showed that the sequence of matrices \(\,\{B_k\}\,\) satisfies the Dennis-Moré condition (4), i.e., the sequence of matrices \(\,\{B_k\}\,\) satisfies hypothesis H4.

On the other hand, SANE, DF-SANE, Ac-DFSANE and NITSOL algorithms were carried out with the same parameters as in respective references given above.

In Table 1, we show the complete list of problems with which we ran our experiments. Starting points were the same as in the respective references.

Table 1 List of problems
Full size table

In Tables 2 and 3 we report the results obtained using the following conventions:

F : :

functions of Table 1.

Method::

algorithm used to solve the problems.

n : :

size of the problem to solve.

k : :

number of iterations required for the algorithms to solve each problem.

Feval : :

number of evaluation of function at each problem.

t : :

cpu time, given in seconds.

\(**:\):

means nonconverge of the algorithm because it infringes the stop criteria.

Table 2 Problems 1 to 10
Full size table
Table 3 Problems 11 to 20
Full size table

The results in Tables 2 and 3 showed good performance of the IFDQ algorithm. First because IFDQ algorithm required the same or fewer iterations than its counterparts in 17.5% of the problems. Second, our algorithm converged on thirty-eight of the problems, that is, IFDQ algorithm converged on \(95\%\) of the experiments carried out.

It is important to mention that although in general when SANE, DF-SANE, Ac-DFSANE and NITSOL converged, they were faster, in terms of CPU time, than IFDQ, but in most cases, that difference was only for a few seconds. This behavior is due to the fact that SANE, DF-SANE and Ac-DFSANE used \(\,\pm F(\varvec{x}_k)\,\) as trial directions, so they do not have to solve a linear system of equation like (3) or make matrix vector products as products made for IFDQ to update \(\,B_k\,\). On the other side, NITSOL makes a single linear search, so generally requires less evaluations of function than IFDQ. In the same way, NITSOL approximate derivatives by finite differences when these are not available nevertheless we think that this could be affecting the convergence of the method since this was the one with the lowest success rate. For the above, IFDQ seems to be a competitive algorithm.

In the second and third columns of Table 4 we show the percentage of experiments in which each algorithm won in terms of CPU time and number of iterations. In last column of this table we show the percentage of success of each algorithm with the experiments.

Table 4 Global convergence
Full size table

The results show the IFDQ algorithm as an equilibrated method since it was the most successful without requiring a large number of iterations or CPU time compared to the other algorithms.

To test the global convergence of the IFDQ algorithm, we experimented with some of the problems by randomly varying the starting point. In all cases, we ran the algorithm with 500 starting points, whose components were uniformly distributed in the interval \(\,[-100,\,100].\,\) In Table 5 we show, for each experiment, the problem, the size of the problem and the success rate of the method.

Table 5 Global convergence
Full size table

The success rate of the algorithm on selected problems shows us a robust method; thus, it would be a good option for solving large-scale nonlinear system of equations.

To finish our experiments, we want to show the inner behavior of the IFDQ algorithm when solving the problem given by the Extended Rosenbrock function.

In Table 6, we show the behavior of the most important parameters in the algorithm when solving the above-mentioned problem. In this table,

$$\begin{aligned} RelRes=\frac{\Vert \varvec{x}_{k+1}-\varvec{x}^*\Vert }{\Vert \varvec{x}_{k}-\varvec{x}^*\Vert } \end{aligned}$$

it helps us to analyze the rate convergence of the algorithm.

Table 6 Inner behavior
Full size table

As we can see in Table 6, \(\,RelRes\,\) converge to zero when \(\,\theta _k\,\) converge to zero, which suppose a superlinear convergence of the algorithm, as we proved in Theorem 5. On the other hand, \(\,\alpha _k=1\,\) for \(\,k>18\,\) just as we proved in Theorem 3.

5 Final remarks

In this work we proposed a new free derivative method for solving, especially, large-scale nonlinear systems of equations. This method takes inexact quasi-Newton directions to build the new iterate and, taking into account that so far it has not been possible to demonstrate that this is a descent direction and seeking to establish global convergence we proposed a two-stage linear search procedure.

For this new method, we show that it enjoys good convergence properties, this is, IFDQ method locally performs very well and, under reasonable hypotheses, has until superlinear convergence.

Numerical experiments showed that IFDQ had a performance according to expected and that this is a competitive method for solving large-scale nonlinear systems of equations.