Skip to main content
SpringerLink
Log in

A linearized second-order scheme for nonlinear time fractional Klein-Gordon type equations

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

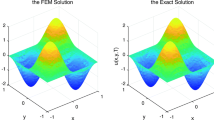
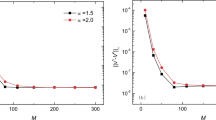
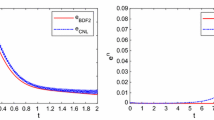
Abstract

We consider difference schemes for nonlinear time fractional Klein-Gordon type equations in this paper. A linearized scheme is proposed to solve the problem. As a result, iterative method need not be employed. One of the main difficulties for the analysis is that certain weight averages of the approximated solutions are considered in the discretization and standard energy estimates cannot be applied directly. By introducing a new grid function, which further approximates the solution, and using ideas in some recent studies, we show that the method converges with second-order accuracy in time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barkai, E., Metzler, R., Klafter, J.: From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 61, 132–138 (2000)

    Article  MathSciNet  Google Scholar 

  2. Fitt, A.D., Goodwin, A.R.H., Ronaldson, K.A., Wakeham, W.A.: A fractional differential equation for a MEMS viscometer used in the oil industry. J. Comput. Appl. Math. 229, 373–381 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  3. Kilbas, A., Srivastava, H., Trujillo, J.: Theory and Applications of Fractional Differential Equations. Elsevier Science and Technology, Amsterdam (2006)

    MATH  Google Scholar 

  4. Meerschaert, M.M., Benson, D.A., Baeumer, B.: Operator lévy motion and multiscaling anomalous diffusion. Phys. Rev. E 63, 1112–1117 (2001)

    Article  Google Scholar 

  5. Meerschaert, M.M., Benson, D.A., Scheffler, H.-P., Baeumer, B.: Stochastic solution of space-time fractional diffusion equations. Phys. Rev. E 65, 1103–1106 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  6. West, B.: Fractional calculus in bioengineering. J. Stat. Phys. 126, 1285–1286 (2007)

    Article  Google Scholar 

  7. Cui, M.: Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 228, 7792–7804 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deng, W.H.: Finite element method for the space and time fractional Fokker-Planck equation. SIAM J. Numer. Anal. 47, 204–226 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  9. Deng, W.H.: Numerical algorithm for the time fractional Fokker-Planck equation. J. Comput. Phys. 227, 1510–1522 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Gao, G.H., Sun, Z.Z., Zhang, H.W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Jin, B., Lazarov, R., Zhou, Z.: Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J. Numer. Anal. 51, 445–466 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Jin, B., Lazarov, R., Zhou, Z.: Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM J. Numer. Anal. 38, A146–A170 (2016)

    MathSciNet  MATH  Google Scholar 

  13. Lei, S.L., Sun, H.W.: A circulant preconditioner for fractional diffusion equations. J. Comput. Phys. 242, 715–725 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu, F., Meerschaert, M.M., McGough, R.J., Zhuang, P., Liu, Q.: Numerical methods for solving the multi-term time-fractional wave-diffusion equation. Fractional Calc. Appl. Anal. 16, 9–25 (2013)

    MathSciNet  MATH  Google Scholar 

  16. Vong, S., Wang, Z.: A high order compact finite difference scheme for time fractional Fokker-Planck equations. Appl. Math. Lett. 43, 38–43 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang, Z., Vong, S.: A high-order exponential ADI scheme for two dimensional time fractional convection-diffusion equations. Comput. Math. Appl. 68, 185–196 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Yuste, S.B., Acedo, L.: An explicit finite difference method and a new Von Neumann-type stability analysis for fractional diffusion equations. SIAM J. Numer. Anal. 42, 1862–1874 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhao, Z., Jin, X.Q., Lin, M.M.: Preconditioned iterative methods for space-time fractional advection-diffusion equations. J. Comput. Phys. 319, 266–279 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Zhuang, P., Liu, F., Anh, V., Turner, I.: New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation. SIAM J. Numer. Anal. 46, 1079–1095 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. El-Sayed, S.M.: The decomposition method for studying the Klein-Gordon equation. Chaos, Solitons Fractals 18, 1025–1030 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  22. Kaya, D., El-Sayed, S.M.: A numerical solution of the Klein-Gordon equation and convergence of the decomposition method. Appl. Math. Comput. 156, 341–353 (2004)

    MathSciNet  MATH  Google Scholar 

  23. Batiha, B., Noorani, M.S.M., Hashim, I.: Numerical solution of sine-Gordon equation by variational iteration method. Phys. Lett. A 370, 437–440 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yusufoğlu, E.: The variational iteration method for studying the Klein-Gordon equation. Appl. Math. Lett. 21, 669–674 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  25. Jafari, H., Saeidy, M., Arab Firoozjaee, M.: Solving nonlinear Klein-Gordon equation with a quadratic nonlinear term using homotopy analysis method. Iran. J. Optim. 1, 162–172 (2009)

    Google Scholar 

  26. Golmankhaneh, A.K., Golmankhaneh, A.K., Baleanu, D.: On nonlinear fractional Klein-Gordon equation. Sig. Process. 91, 446–451 (2011)

    Article  MATH  Google Scholar 

  27. Jafari, H., Tajadodi, H., Kadkhoda, N., Baleanu, D.: Fractional subequation method for Cahn-Hilliard and Klein-Gordon equations. Abstr. Appl. Anal. (2013). doi:10.1155/2013/587179

  28. Cui, M.: Fourth-order compact scheme for the one-dimensional sine-Gordon equation. Numer. Meth. Part. Differ. Equ. 25, 685–711 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  29. Vong, S., Wang, Z.: A compact difference scheme for a two dimensional fractional Klein-Gordon equation with Neumann boundary conditions. J. Comput. Phys. 274, 268–282 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Vong, S., Wang, Z.: A high-order compact scheme for the nonlinear fractional Klein-Gordon equation. Numer. Meth. Part. Differ. Equ. 31, 706–722 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Chen, H., Lu, S., Chen, W.: A fully discrete spectral method for the nonlinear time fractional Klein-Gordon equation. Taiwan. J. Math. 21, 231–251 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  32. Dehghan, M., Abbaszadeh, M., Mohebbi, A.: An implicit RBF meshless approach for solving the time fractional nonlinear sine-Gordon and Klein-Gordon equations. Eng. Anal. Bound. Elem. 50, 412–434 (2015)

    Article  MathSciNet  Google Scholar 

  33. Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Hao, Z.P., Sun, Z.Z.: A linearized high-order difference scheme for the fractional Ginzburg-Landau equation. Numer. Meth. Part. Differ. Equ. (2016). doi:10.1002/num.22076

  35. Ran, M., Zhang, C.: A conservative difference scheme for solving the strongly coupled nonlinear fractional schrödinger equations. Commun. Nonlin. Sci. Numer. Simulat. 41, 64–83 (2016)

    Article  Google Scholar 

  36. Wang, D., Xiao, A., Yang, W.: A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 272, 644–655 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhao, X., Sun, Z.Z., Hao, Z.P.: A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J. Sci. Comput. 36, A2865–A2886 (2014)

    Article  MATH  Google Scholar 

  38. Liao, H.L., Zhao, Y., Teng, X.H.: A weighted ADI scheme for subdiffusion equations. J. Sci. Comput. (2016). doi:10.1007/s10915-016-0230-9

  39. Liao, H.L., Zhao, Y., Teng, X.H.: Convergence of a weighted compact ADI scheme for fractional diffusion-wave equations. submitted

  40. Quarteroni, A., Valli, A.: Numerical Approximation of Partial Diferential Equations. Springer, Berlin (1997)

    Google Scholar 

  41. Sun, Z.Z.: Numerical Methods of Partial Differential Equations, 2nd edn. Science Press, Beijing (2012)

    Google Scholar 

  42. Vong, S., Lyu, P., Chen, X., Lei, S.L.: High order finite difference method for time-space fractional differential equations with Caputo and Riemann-Liouville derivatives. Numer. Algor. 72, 195–210 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  43. Sun, Z.Z., Wu, X.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, 193–209 (2006)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgment

The authors would like to thank the referees for their comments which improve the paper significantly. We also want to thank Prof. Honglin Liao for the helpful discussion on the estimates of Lemmas 2.2 and 2.3.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Macau, Avenida da Universidade, Macau, China

    Pin Lyu & Seakweng Vong

Authors
  1. Pin Lyu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Seakweng Vong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seakweng Vong.

Additional information

This research is supported by the Macao Science and Technology Development Fund 010/2015/A and the grant MYRG2015-00064-FST from University of Macau.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lyu, P., Vong, S. A linearized second-order scheme for nonlinear time fractional Klein-Gordon type equations. Numer Algor 78, 485–511 (2018). https://doi.org/10.1007/s11075-017-0385-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-017-0385-y

Keywords

Search

Navigation