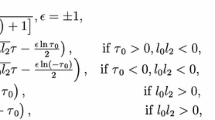1 Introduction

Many mathematical models used in science and engineering are expressed using differential equations. Finding exact solutions of these equations is very important for understanding and interpreting problems that express physical processes. Nonlinear partial differential equations (NLPDEs) are encountered in various applications of biology, chemistry, mathematics and physics. Even the simple solutions of these equations frequently appear as examples explaining the basic principles of theories in different fields. Evolution equations are a special case of NLPDEs. These equations are frequently encountered in applications of fields such as physics and mechanics, as well as in mathematics. Navier–Stokes and Euler equations are used in fluid mechanics, Cahn - Hilliard equation in material science, and Klein - Gordon and Schrodinger equations in quantum mechanics. Nonlinear evolution equations (NLEEs) model physical phenomena that occur in many fields of science, such as physics, mechanics, engineering, materials science, fluid mechanics, solid state physics, chemistry, plasma physics, chemical physics, optical fibers, geochemistry, biology, chemical kinetics, deep water waves, oceanography, signal processing and system identification. For this reason, it is very important to obtain solutions of such equations in order to better understand the physical phenomenon modeled, or in other words, to have a better look at the physical characteristics of the problem in question and to discover possible applications. Finding solutions to such equations is possible with the help of developed methods and computer programs. A range of algorithms have been applied to nonlinear models, such as the Sardar- sub equation method [1, 2], the new extended direct algebraic method [3, 4], the \(\left( G'/G\right) \) expansion method [5], the extended tanh-function technique [6, 7], the tanh-coth method [8], the Riccati equation expansion method [9],the Lie symmetry technique [10, 11], the extended hyperbolic function method [12], the modified exponential function method [13], the modified rational sine-cosine functions [14], the modified \(\left( G'/G^2 \right) \) expansion method [15,16,17,18,19], the sine-cosine method [20], the first integral method [21], the extended modified auxiliary equation mapping method [22,23,24], the homotopy analysis method [25], the new \(\phi ^6-\)model expansion method [26], the generalized projective Riccati equations method [27] and the generalized exponential rational function method [28] so on.

The generalization of classical integer differential equations gives rise to fractional equations, which play an important and central role in countless branches of physics, mathematics and engineering. Since models built with fractional derivative nonlinear equations give results closer to reality; kinetic models are increasingly used in applications in fields such as acoustics,anomalous diffusion, engineering, control theory, image and signal processing,vehicular traffic flow [29,30,31,32]. Scientific applications using the definition of fractional analysis have yielded remarkable results in the last years. The researchers have used some derivatives that have fractional order such as the Caputo fractional derivative [33], the fractional Grunwald-Letnikov derivative [34], the Riemann- Liouville definition of fractional derivative [35, 36], the modified Riemann-Liouville derivative [37], Atangana- Baleanu derivative [38, 39] and Caputo-Liouville generalized fractional derivative [40, 41] an so on [42,43,44,45]. To give a few examples of studies using these derivatives: The human immunodeficiency virus (HIV) and AIDS are propagated using a fractional derivative of the Caputo type in [46], the time-fractional nonlinear Calogero-Bogoyavlenskii-Schiff equation with conformable derivative is considered in [47], the fractional order dual-mode nonlinear Schrodinger equation with time-space conformable sense is studied in [48].

Being at the center of natural and industrial processes, foam has attracted great attention among researchers in both academia and industry. The physical importance of foam drainage equations lies in their ability to describe the dynamics of foam structure and stability over time.The research centers around three topics that are often considered separately but are interconnected: drainage, coarsening and rheology. Foam drainage is called the flow of liquid through liquid-filled channels and the intersections of four channels between bubbles. This flow driven by gravity and capillarity. Foams’drainage plays a very important role in foam stability. Foam drainage equations help to analyse the stability of foam structures by predicting how liquid films between foam bubbles thin and break away over time. This understanding is critical for applications such as foam stabilization in consumer products, firefighting foams and food foams. Although many studies have been carried out to date, investigations on the dynamics of foam drainage are still incomplete. Foams are the subject of intensive studies both in practical and scientific terms, as they are encountered in many technological processes and applications. Foams are noteworthy for both ordinary people and scientists because of their widespread presence in foods and personal care products such as lotions and creams, and because foams often occur during cleaning and scrubbing of clothes [49]. Another area of application for foams is the food and chemical, material science and firefighting industries [50]. By manipulating factors such as foam composition, temperature and additives, drainage rates can be controlled to achieve desired foam properties. Foam drainage equations are also of significance in materials science, where they are employed to comprehend the behavior of porous materials and to facilitate the development of novel materials with distinctive properties. By investigating foam drainage, researchers can gain insight into the behavior of porous media and their applications in domains such as insulation, filtration and catalysis. These applications in daily life are a source of motivation for scientific researches. The foam-drainage equation [51, 52], which is a NLEE, is given by

$$\begin{aligned} u_t+\left( u^2 -\frac{\sqrt{u}}{2}u_x\right) _x=0, \end{aligned}$$
(1)

where x and t are scaled position and time coordinates, respectively. u is the cross section of a channel formed where three films meet. This equation is investigated by various researchers such as [53,54,55,56,57]. In [58], the following foam draigne equation was considered

$$\begin{aligned} u_t=\frac{1}{2}uu_{xx}+2u^2u_x+u_x^2, \end{aligned}$$
(2)

and the modified simple equation method, the exp-function method, the soliton ansatz method, the Riccati equation expansion method and the \( G^{\prime }/G\)-expansion method are used to construct the exact solutions.

In 2010 [59], the foam drainage equation with time and space-fractional derivatives of following form was studied:

$$\begin{aligned}{} & {} D_t^\alpha u=\frac{1}{2}uu_{xx}-2u^2D_x^\beta u\nonumber \\{} & {} \qquad \qquad +(D_x^\beta )^2,\ \ \ 0<\alpha , \beta \le 1, x>0, \end{aligned}$$
(3)

where the fractional derivatives are considered in the Caputo sense and \(\alpha \) denotes the fractional orders of the derivatives with respect to independent variable t. The numerical solutions of (3) were obtained in [59]. The exact solutions were obtained in [60] for the Eq. (3). In 2014 [61], authors considered the Eq. (3) to find solutions of the space-time fractional foam drainage equation in the sense of Jumarie’s modified Riemann- Liouville derivative. In 2021 [62], the space-time fractional foam drainage equation in the sense of conformable fractional derivative was considered and closed form soliton solutions were obtained. The two-mode foam drainage model was presented for the first time in [63]

$$\begin{aligned}{} & {} u_{tt}-s^2u_{xx}+\left( \frac{\partial }{\partial t} -\delta s \frac{\partial }{ \partial x} \right) \nonumber \\{} & {} \quad \left( a u^2u_x+b (u_x)^2+\gamma u u_{xx} \right) =0, \end{aligned}$$
(4)

where u is the unknown function. s is the phase velocity, \(\delta \) shows the nonlinearity parameter, and \(a,b,\gamma \) are real scalers. This model describes the motion of instantaneous symmetric double-waves and their interaction depends on two involved parameters known as nonlinearity and phase-velocity. For \(s=0\), \(\alpha =2,\beta =-1,\gamma =-1/2\), this equation changes to the Eq. (1). With the motivation of the above studies, in this paper we will consider the following conformable space-time foam drainage equation in two mode

$$\begin{aligned}{} & {} D_{t}^{2\alpha }u-s^{2}D_{x}^{2\beta }u+\left( D_{t}^{\alpha } -\delta sD_{x}^{\beta }\right) \nonumber \\{} & {} \quad \left( au^{2}D_{x}^{\beta }u+b(D_{x}^{\beta }u)^{2}+\gamma uD_{x}^{2\beta }u\right) =0, \end{aligned}$$
(5)

where \(\alpha \) and \(\beta \) ( \(\alpha ,\beta \in (0,1]\), \(t>0\)) denote the orders of the derivatives with respect to independent variables t and x, respectively. For integer boundary value 1 for \( \alpha \) and \(\beta \) the foam drainage Eq. (5) changes to the Eq. (4). The two mode type NLEEs, the fact that it has recently attracted the attention of many researchers in the field of nonlinear sciences due to its examination of simultaneous wave interactions in dual modes, the importance of the foam drainage equation in technological and practical sciences, and obtaining results closer to reality with fractional derivatives are some of our motivations in examining this model. The conformable derivative brings us a lot of convenience when it is used to model many physical problems, because the differential equations with conformable fractional derivative are easier to solve numerically than those associated with the Riemann-Liouville or Caputo fractional derivative.

The main purpose of the present study is to find the exact travelling wave solutions for the Eq. (5) by means of the generalized exponential rational function method (GERFM) and the improved version of the Bernoulli sub-equation function method (IBSEFM). GERFM is a generalization of the exponential rational function method and was introduced by Ghanbari et al in 2018 [64]. This method stands out because it is very effective and relatively easy to apply in obtaining various solutions of the model under consideration. Because GERFM includes many free parameters that give different types of default solution shapes, it is much more powerful than other existing methods [65]. The IBSEFM, derived from the Bernoulli sub-equation function method, is a simple, important and sophisticated algebraic approach for finding reliable and trustworthy solutions to NLPDEs [66, 67]. The results are far-reaching, as the solutions obtained through this methodology not only open the doors to solving urgent problems, but also form the basis for comprehensive research scrutiny. It is worth noting that the models mentioned have not yet been studied using the GERFM and IBSEFM. Consequently, the aim of this study is to improve the accuracy of possible soliton solutions to the underlying equation using these techniques. Graphical representations of the solutions found with specific values for the free parameters are described using the 3D plots. The proposed methods are effective in constructing a variety of soliton solutions, faster to simulate and flexible. In addition to the advantages of the methods discussed, they also have some disadvantages and limitations. Both methods may not be applicable to all types of NLPDEs, but for some specific NLPDEs, these methods are important in obtaining exact solutions. The limitations of the applied techniques include their limited applicability to specific data sets and difficulties in parameterization. Therefore, the full solution spectrum and all potential behaviors of the underlying models may not be fully captured or taken into account. In this sense, by applying modified versions of the alternative techniques, researchers aim to eliminate these limitations by improving their adaptability to different types of equations and computational performance. To the best of the authors’ knowledge, this type of investigation has not been carried out before for the model under consideration and is therefore interesting to report here.

The rest of the article is arranged as follows: Sect. 2 is dedicated to the properties of the conformable derivatives. In Sect. 3, the descriptions of proposed methods are given. In Sect. 4, the mathematical analysis of the Eq. (5) is given. In Sects. 5 and 6, we apply these methods to the NLEE pointed out earlier; in Sect. 7, we show some graphical illustrations of our obtained solutions. Conclusions are drawn in Sect. 8.

2 Conformable derivative

The definition and properties of the concept called “conformable derivative” by R. Khalil and et al. [68, 69] are given below.

Definition

[68]: Let \(\varphi :[0,\infty )\rightarrow {\mathbb {R}} \) be a function, then its conformable derivative of order \(\alpha \) is defined as

$$\begin{aligned} D^{\alpha }_t\left( \varphi \right) \left( t\right) =\lim _{\epsilon \rightarrow 0} \frac{\varphi \left( t+\epsilon t^{1-\alpha }\right) -\varphi \left( t\right) }{\epsilon } \end{aligned}$$

for all \(t>0,\alpha \in \left( 0,1\right] .\)

Theorem 1

Let \( D^{\alpha }_t\) be a conformable derivative operator with order \(\alpha \) and \(\alpha \in (0,1],\) \(\varphi ,\psi \) be \(\alpha -\) differentiable at point \(\ t>0.\) Then [68, 70],

  1. (1)

    \( D^{\alpha }_t\left( a\varphi +b\psi \right) =a D^{\alpha }_t\left( \varphi \right) +b D^{\alpha }_t(\psi ),\) \(\forall a,b\in {\mathbb {R}}.\)

  2. (2)

    \( D^{\alpha }_t\left( t^{p}\right) =pt^{p-\alpha },\forall p\in {\mathbb {R}}.\)

  3. (3)

    \( D^{\alpha }_t\left( \varphi \psi \right) =\varphi D^{\alpha }_t\left( \psi \right) +\psi D^{\alpha }_t\left( \varphi \right) .\)

  4. (4)

    \( D^{\alpha }_t\left( \frac{\varphi }{\psi }\right) =\frac{\psi D^{\alpha }_t\left( \varphi \right) -\varphi D^{\alpha }_t\left( \psi \right) }{\psi ^{2}}.\)

  5. (5)

    \( D^{\alpha }_t\left( \lambda \right) =0,\) for all constant functions \( \varphi (t)=\lambda .\)

  6. (6)

    If f is differentiable, then \( D^{\alpha }_t\left( \varphi \right) (t)=t^{1-\alpha }\frac{d\varphi }{dt}(t).\)

3 Conceptualism of the methodology

This section proposes the detailed algorithms of the methods to to analyze the Eq. (5). Considering a NLPDE for \(\eta (x,t)\) as follows:

$$\begin{aligned} \Psi (\eta ,\eta _{x},\eta _{t},\eta _{xx},...)=0. \end{aligned}$$
(6)

The discussed NLPDE can be reduced to ordinary differential equation (ODE)

$$\begin{aligned} \Psi (u,u^{\prime },u^{\prime \prime },u^{\prime \prime \prime },...)=0. \end{aligned}$$
(7)

using the following transformation:

$$\begin{aligned} u=u(\zeta ),\zeta =\lambda x+vt. \end{aligned}$$
(8)

3.1 GERFM: its outline

In this part, the basic steps of the GERFM [64] will be given. A solution to Eq. (7) will be assumed to be of the subsequent form:

$$\begin{aligned} u(\zeta )=A_{0}+\sum _{k=1}^{N}\left( A_{k}\varphi (\zeta )^{k}+B_{k}\varphi (\zeta )^{-k} \right) \end{aligned}$$
(9)

where

$$\begin{aligned} \varphi (\zeta )=\frac{p_{1}e^{\theta _{1}\zeta }+p_{2}e^{\theta _{2}\zeta } }{p_{3}e^{\theta _{3}\zeta }+p_{4}e^{\theta _{4}\zeta }}. \end{aligned}$$
(10)

Here \(A_{0}\), \(A_{1},A_{2},...,A_{N},B_{1},B_{2},...,B_{N}\) and \(p_{i}\), \(\theta _{i}\) \((1\le i\le 4)\), are constants and the balancing term N in the Eq. (9) is calculated with the help of the homogeneous balance principle. If (9) is substituted for \(u(\zeta )\) in the ODE (7) and necessary adjustments are made, an equation \(\digamma (\zeta ,e^{\theta _{1}\zeta },e^{\theta _{2}\zeta },e^{\theta _{3}\zeta },e^{\theta _{4}\zeta })=0.\) containing \(\zeta \) and \(e^{\theta _{i}\zeta }\) \((1\le i\le 4)\) is obtained. A system of equations is obtained by setting the coefcients of all powers of \(\digamma \) to zero. Finally, by solving the resulting system, relations regarding the coefficients are obtained. Substituting these values in Eq. (9), the explicit shape of the solutions of Eq. (6) will be extracted.

3.2 IBSEFM: its outline

In this part, the basic steps of the IBSEFM [71] will be given. Consider the NLPDE (6) and the ODE (7) with the wave transformation. According to this method, the solution of (7) is supposed as

$$\begin{aligned} u(\zeta )\!=\!\frac{\sum _{i=0}^{n}a_{i}q^{i}}{\sum _{j=0}^{m}b_{j}q^{j}}=\frac{ a_{0}+a_{1}q+a_{2}q^{2}\!+\!\ldots \!+\!a_{n}q^{n}}{b_{0}\!+\!b_{1}q+b_{2}q^{2}+\ldots \!+\!b_{m}q^{m}}.\nonumber \\ \end{aligned}$$
(11)

The solution of the improved Bernoulli equation is \(q=q(\zeta )\)

$$\begin{aligned}{} & {} q^{\prime }(\zeta )=Bq(\zeta )+Aq^M(\zeta ),\ \ \ \ \ A,B\ne 0,\nonumber \\{} & {} \quad M\in {\mathbb {R}}-\left\{ 0,1,2\right\} . \end{aligned}$$
(12)

Substituting above relations in Eq. (7), it yields us an equation of polynomial \(\Omega (q(\zeta ))\) of \(q=q(\zeta )\);

$$\begin{aligned} \Omega (q(\zeta ))=\rho _{s}q^{s}(\zeta )+\ldots +\rho _{1}q(\zeta )+\rho _{0}=0. \end{aligned}$$
(13)

Using the principle of balance, the relationship between the numbers m, n, and M can be found. Let the coefficients of \(\Omega (q(\zeta ))\) all be zero will yield an algebraic equations system:

$$\begin{aligned} \rho _{i}=0,i=0,1,2,\ldots ,s. \end{aligned}$$
(14)

Solving (14), we will specify the values of \(a_{i},(i=0,1,...,n)\) and \(b_{j},(j=0,1,...,m)\). When we solve nonlinear Bernoulli differential Eq. (12), we obtain the following two case according to A and B:

$$\begin{aligned} q(\zeta )\left[ -\frac{A}{B}+\frac{E}{e^{B(M-1)\zeta }}\right] ^{\frac{1}{1-M} }, A\ne B \end{aligned}$$
(15)

and,

$$\begin{aligned}{} & {} q(\zeta )=\left[ \frac{M-1+(M+1)\tanh (\frac{B(1-M)\zeta }{2})}{1-\tanh (\frac{ B(1-M)\zeta }{2})} \right] ^{\frac{1}{1-M}},\nonumber \\{} & {} \quad A= B, E\in {\mathbb {R}}. \end{aligned}$$
(16)

Using Eqs. (15) and (16), the desired solutions of Eq. (6) can be obtained.

4 Mathematical analysis

The following transformation should be used to reduce Eq. (5) to an ODE.

$$\begin{aligned} {u}(x,t)={u}(\xi ),\ \ \,\xi =-\frac{k}{\beta }x^{\beta }+\frac{w}{\alpha } t^{\alpha }. \end{aligned}$$
(17)

Here, k, w constants and w shows the speed of travelling wave. Using (17), Eq. (5) can be converted into:

$$\begin{aligned}{} & {} \left( {w}^{2}-{s}^{2}\right) {u}^{\prime \prime }+2\,\left( akw-\delta \,sa{ k}^{2}\right) u\left( {u}^{\prime }\right) ^{2}\nonumber \\{} & {} +\left( akw-\delta \,sa{k} ^{2}\right) u^{2}{u}^{\prime \prime }+\left( \gamma \,{k}^{2}w-\delta \,s\gamma \,{k}^{3}\right) u^{\prime \prime \prime }u \nonumber \\{} & {} +\left( \gamma \,{k}^{2}w-\delta \,s\gamma \,{k}^{3}+2\,b{k}^{2}w-2\delta \,sb{k}^{3}\right) u^{\prime \prime }{u}^{\prime }=0.\nonumber \\ \end{aligned}$$
(18)

If the above equation is integrated with respect to \(\xi \) once, the following equation is obtained.

$$\begin{aligned}{} & {} \left( {w}^{2}-{s}^{2}\right) {u}^{\prime }+\left( akw-\delta \,sa{k} ^{2}\right) u^{2}{u}^{\prime }\nonumber \\{} & {} +\left( \gamma \,{k}^{2}w-\delta \,s\gamma \,{k }^{3}\right) u^{\prime \prime }u\nonumber \\{} & {} +\left( b{k}^{2}w-\delta \,sb{k}^{3}\right) \left( {u}^{\prime }\right) ^{2}=0. \end{aligned}$$
(19)

5 Main outcomes of solving model Eq. (5) using GERFM

Balancing \(u^{2}u^{\prime }\) and \(uu^{\prime \prime }\) in Eq. (19) yields N is 1. Accordingly, from (9), Eq. (5) admits a solution of the following form:

$$\begin{aligned} u(\zeta )=A_{0}+A_{1}\varphi (\xi )+\frac{B_{1}}{\varphi (\xi )}. \end{aligned}$$
(20)
Table 1 \(p=[p_{1},p_{2},p_{3},p_{4}]\), \(\theta =[\theta _{1},\theta _{2},\theta _{3},\theta _{4}]\) and \( \varphi (\xi )\) is given in (10)
Full size table

Using the method presented in the Section 3, we obtain non-trivial solutions of (5) as follows:

Group 1: If the corresponding function \(\varphi \) in the Table 1 for \(p=[1,2,1,1]\) and \(\theta =[-1,1,-1,1]\) is used, we get:

$$\begin{aligned}{} & {} \text {Set 1.1}:\nonumber \\{} & {} \left\{ \begin{array}{l} {A_{0}}=-\frac{3}{4}\,{B_{1}},{A_{1}}=0,{B_{1}}={B_{1}},k=-\,{\frac{{B_{1}} \,a}{4\left( b+2\,\gamma \right) }}, \\ \\ w\!=\!{\dfrac{{a}^{2}{{B_{1}}}^{3}b\!\pm \!\sqrt{{a}^{4}{{B_{1}}}^{6}{b} ^{2}\!\!+\!\!16384\left( b\!+\!2\gamma \right) ^{4}{s}^{2}\!+\!64{{B_{1}}}^{4}{a} ^{3}\delta b\left( b\!+\!2\gamma \right) s}}{128\left( b\!+\!2\,\gamma \right) ^{2}}.}\!\!\! \end{array} \right\} \nonumber \\ \end{aligned}$$
(21)

Inserting these above values of \(A_0,A_1,k,w\) into Eq. (20), we get

$$\begin{aligned}{} & {} u_{1.1}(x,t)\nonumber \\{} & {} \quad =-\frac{3}{4}\,{B_{1}}\nonumber \\{} & {} \quad +\frac{2\,{B_{1}}\,\cosh \left( \,{\frac{{ B_{1}}\,a{x}^{\beta }}{4\left( b\!+\!2\,\gamma \right) \beta }}\!-\!{\frac{w{t} ^{\alpha }}{\alpha }}\right) }{3\,\cosh \left( \,{\frac{{B_{1}}\,a{x}^{\beta }}{4\left( b\!+\!2\,\gamma \right) \beta }}\!-\!{\frac{w{t}^{\alpha }}{\alpha }} \right) \! -\!\sinh \left( \,{\frac{{B_{1}}\,a{x}^{\beta }}{4\left( b\!+\!2\,\gamma \right) \beta }}\!-\!{\frac{w{t}^{\alpha }}{\alpha }}\right) },\nonumber \\ \end{aligned}$$
(22)

where w is given in (21).

$$\begin{aligned}{} & {} \text {Set 1.2}:\nonumber \\{} & {} \left\{ \begin{array}{l} {A_{0}}=-\frac{3}{2}\,{A_{1}},{A_{1}}={A_{1}},{B_{1}}=0,k=\,{\frac{{A_{1}}\,a }{2\left( b+2\,\gamma \right) }}, \\ \\ w\!=\!-\!{\dfrac{{{A_{1}}}^{3}{a}^{2}b\!\pm \!\sqrt{{a}^{4}{{A_{1}}}^{6}{b} ^{2}\!+\!256\left( b\!+\!2\gamma \right) ^{4}{s}^{2}\!+\!16{{A_{1}}}^{4}{a} ^{3}\delta b\left( b\!+\!2\gamma \right) s}}{16\left( b\!+\!2\gamma \right) ^{2}}.}\!\!\! \end{array} \right\} \nonumber \\ \end{aligned}$$
(23)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{1.2}(x,t)=-\frac{3}{2}\,\,{A_{1}}\nonumber \\{} & {} +\frac{1}{2}\,\,{A_{1}}\,\frac{\left( 3\,\cosh \left( {\frac{{A_{1}}\,a{x}^{\beta }}{2\left( b+2\,\gamma \right) \beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) +\sinh \left( \,{\frac{{ A_{1}}\,a{x}^{\beta }}{2\left( b+2\,\gamma \right) \beta }}+{\frac{w{t} ^{\alpha }}{\alpha }}\right) \right) }{\cosh \left( {\frac{{A_{1}}\,a{x} ^{\beta }}{2\left( b+2\,\gamma \right) \beta }}+{\frac{w{t}^{\alpha }}{ \alpha }}\right) }.\nonumber \\ \end{aligned}$$
(24)

Group 2: If the corresponding function \(\varphi \) in the Table 1 for \(p=[-3,-1,1,1]\) and \(\theta =[1,-1,1,-1]\) is used, we get:

$$\begin{aligned}{} & {} \text {Set 2.1}: \left\{ \begin{array}{c} {A_{0}}=\frac{2}{3}{B_{1}},{A_{1}}=0,{B_{1}}={B_{1}},k=\,{\frac{a{B_{1}}}{ 3\left( 2\,\gamma +b\right) }},w=w, \\ \\ \delta =3\,{\frac{\left( 2\,\gamma +b\right) \left( -108\,\gamma \,\left( s-w\right) \left( s+w\right) \left( \gamma +b\right) +\left( -27\,{s} ^{2}+27\,{w}^{2}\right) {b}^{2}+w{a}^{2}{{B_{1}}}^{3}b\right) }{bs{a}^{3}{{ B_{1}}}^{4}}.}\!\! \end{array} \right\} \end{aligned}$$
(25)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{2.1}(x,t)=\frac{2}{3}\,{B_{1}}\nonumber \\{} & {} \qquad \qquad \qquad +\frac{2\,{B_{1}}\,\cosh \left( \,{\frac{a{ B_{1}}\,{x}^{\beta }}{3\left( 2\,\gamma +b\right) \beta }}+{\frac{w{t} ^{\alpha }}{\alpha }}\right) }{-4\,\cosh \left( \,{\frac{a{B_{1}}\,{x} ^{\beta }}{3\left( 2\,\gamma +b\right) \beta }}+{\frac{w{t}^{\alpha }}{ \alpha }}\right) -2\,\sinh \left( \,{\frac{a{B_{1}}\,{x}^{\beta }}{3\left( 2\,\gamma +b\right) \beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) }. \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \text {Set 2.2}:\left\{ \begin{array}{l} {A_{0}}=2\,{A_{1}},{A_{1}}={A_{1}},{B_{1}}=0,k=-{\frac{a{A_{1}}}{2\,\gamma +b }},w=w, \\ \\ \delta =-{\frac{\left( 2\,\gamma +b\right) \left( \left( 4\,{s}^{2}-4\,{w} ^{2}\right) {\gamma }^{2}+\left( 4\,{s}^{2}-4\,{w}^{2}\right) \gamma \,b+\left( -{w}^{2}+{s}^{2}\right) {b}^{2}+{a}^{2}w{{A_{1}}}^{3}b\right) }{bs {a}^{3}{{A_{1}}}^{4}}.} \end{array} \right\} \end{aligned}$$
(27)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{2.2}(x,t)=2\,{A_{1}}\nonumber \\{} & {} \qquad \qquad \qquad +\,{A_{1}}\,\frac{\left( \!-\!4\,\cosh \left( {\frac{a{ A_{1}}\,{x}^{\beta }}{\left( 2\,\gamma +b\right) \beta }}\!-\!{\frac{w{t} ^{\alpha }}{\alpha }}\right) \!+\!2\,\sinh \left( {\frac{a{A_{1}}\,{x}^{\beta }}{ \left( 2\,\gamma \!+\!b\right) \beta }}\!-\!{\frac{w{t}^{\alpha }}{\alpha }}\right) \right) }{2\cosh \left( {\frac{a{A_{1}}\,{x}^{\beta }}{\left( 2\,\gamma \!+\!b\right) \beta }}-{\frac{w{t}^{\alpha }}{\alpha }}\right) }. \nonumber \\ \end{aligned}$$
(28)

Group 3: If the corresponding function \(\varphi \) in the Table 1 for \(p=[1,1,1,-1]\) and \(\theta =[1,-1,1,-1]\) is used, we get:

$$\begin{aligned}{} & {} \text {Set 3.1}:\left\{ \begin{array}{l} {A_{0}}=0,{A_{1}}=0,{B_{1}}={B_{1}},k={\frac{{B_{1}}\,a}{b+2\,\gamma }}, \\ \\ w=-\,{\frac{b{a}^{2}{{B_{1}}}^{3}\pm \sqrt{\left( {a}^{4}{{B_{1}}}^{6}+4\,{{ B_{1}}}^{4}s\delta \,{a}^{3}\right) {b}^{2}+4\,{s}^{2}\left( {b}^{4}+16\,{ \gamma }^{4}+32\,{\gamma }^{3}b+24\,{\gamma }^{2}{b}^{2}\right) +\left( 32\,{ s}^{2}{b}^{3}+8\,{a}^{3}\delta \,s{{B_{1}}}^{4}b\right) \gamma }}{2\left( b+2\,\gamma \right) ^{2}}.} \end{array} \right\} \end{aligned}$$
(29)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{3.1}(x,t)={B_{1}}\,\sinh \left( {\frac{{B_{1}}\,a{x}^{\beta }}{\left( b+2\,\gamma \right) \beta }}\right. \nonumber \\ {}{} & {} \qquad \qquad \qquad \left. +{\frac{w{t}^{\alpha }}{\alpha }}\right) \left( \cosh \left( {\frac{{B_{1}}\,a{x}^{\beta }}{\left( b+2\,\gamma \right) \beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) \right) ^{-1}. \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \text {Set 3.2}:\left\{ \begin{array}{l} {A_{0}}=0,{A_{1}}={A_{1}},{B_{1}}=0,k={\frac{{A_{1}}\,a}{b+2\,\gamma }}, \\ \\ w=-{\frac{{a}^{2}{{A_{1}}}^{3}b\pm \sqrt{4\,{s}^{2}\left( {b}^{4}+16\,{\gamma } ^{4}+32\,{\gamma }^{3}b+24\,{\gamma }^{2}{b}^{2}\right) +8\,bs\left( {a}^{3}{ {A_{1}}}^{4}\delta +4\,{b}^{2}s\right) \gamma +{a}^{3}{{A_{1}}}^{4}\left( {{ A_{1}}}^{2}a+4\,\delta \,s\right) {b}^{2}}}{2\left( b+2\,\gamma \right) ^{2}}.} \end{array} \right\} \end{aligned}$$
(31)

Therefore, the solution of (19) is given by

$$\begin{aligned}{} & {} u_{3.2}(x,t)={A_{1}}\,\cosh \left( {\frac{{A_{1}}\,a{x}^{\beta }}{\left( b+2\,\gamma \right) \beta }}\right. \nonumber \\ {}{} & {} \qquad \qquad \qquad \left. +{\frac{w{t}^{\alpha }}{\alpha }}\right) \left( \sinh \left( {\frac{{A_{1}}\,a{x}^{\beta }}{\left( b+2\,\gamma \right) \beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) \right) ^{-1}. \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \text {Set 3.3}:\left\{ \begin{array}{l} {A_{0}}=0,{A_{1}}={\frac{\left( b+2\,\gamma \right) k}{a}},{B_{1}}={\frac{ \left( b+2\,\gamma \right) k}{a}},k=k, \\ \\ w=-{\frac{2\,{b}^{2}{k}^{3}+4\,\gamma \,{k}^{3}b\pm \sqrt{{s}^{2}{a}^{2}+4\,{b} ^{2}\left( b+2\,\gamma \right) ^{2}{k}^{6}+4\,a\delta \,sb\left( b+2\,\gamma \right) {k}^{4}}}{a}.} \end{array} \right\} \end{aligned}$$
(33)

As a result, one derives a wave solution for (19) as

$$\begin{aligned}{} & {} u_{3.3}(x,t)=\left( b+2\,\gamma \right) k\frac{\cosh \left( {\frac{k{x} ^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) }{a\sinh \left( { \frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) } \nonumber \\ {}{} & {} \qquad \qquad \quad +\left( b+2\,\gamma \right) k\frac{\sinh \left( {\frac{k{x}^{\beta }}{\beta } }+{\frac{w{t}^{\alpha }}{\alpha }}\right) }{{a}\cosh \left( {\frac{k{x} ^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) }. \end{aligned}$$
(34)

Group 4: If the corresponding function \(\varphi \) in the Table 1 for \(\theta =[0,0,0,1]\) and \(p=[-1,0,1,1]\) is used, we get:

$$\begin{aligned} \text {Set 4.1}:\left\{ \begin{array}{l} {A_{0}}=\,{\frac{\left( b+2\,\gamma \right) k}{2a}},{A_{1}}={\frac{\left( b+2\,\gamma \right) k}{a}},{B_{1}}=0,k=k, \\ \\ w=\,{\frac{-{b}^{2}{k}^{3}-2\,\gamma \,{k}^{3}b\pm \sqrt{{b}^{4}{k}^{6}+4\,{b} ^{3}{k}^{6}\gamma +4\,{b}^{2}{k}^{6}{\gamma }^{2}+64\,{a}^{2}{s}^{2}+16\,a{k} ^{4}s{b}^{2}\delta +32\,a\delta \,s\gamma \,{k}^{4}b}}{8a}.} \end{array} \right\} \end{aligned}$$
(35)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{4.1}(x,t)=\,{\frac{\left( b+2\,\gamma \right) k}{2a}}\nonumber \\{} & {} \qquad \qquad \qquad -\frac{\left( b+2\,\gamma \right) k}{a}\left( 1+{{e}^{{\frac{k{x}^{\beta }}{\beta }}+\,{ \frac{\left( -{b}^{2}{k}^{3}-2\,\gamma \,{k}^{3}b+\sqrt{{b}^{4}{k}^{6}+4\,{b} ^{3}{k}^{6}\gamma +4\,{b}^{2}{k}^{6}{\gamma }^{2}+64\,{a}^{2}{s}^{2}+16\,a{k} ^{4}s{b}^{2}\delta +32\,a\delta \,s\gamma \,{k}^{4}b}\right) {t}^{\alpha }}{ 8a\alpha }}}}\right) ^{-1}. \end{aligned}$$
(36)

Group 5: If the corresponding function \(\varphi \) in the Table 1 for \(p=[-3,-2,1,1]\) and \(\theta =[0,1,0,1]\) is used, we get:

$$\begin{aligned} \text {Set 5.1}:\left\{ \begin{array}{l} {A_{0}}=-\,{\frac{5k\left( 2\,\gamma +b\right) }{2a}},{A_{1}}=0,{B_{1}}=-6\,{ \frac{k\left( 2\,\gamma +b\right) }{a}}, \\ \\ w=-\,{\frac{2\,\gamma \,{k}^{3}b+{k}^{3}{b}^{2}\pm \sqrt{4\,{\gamma }^{2}{k}^{6} {b}^{2}+4\,\gamma \,{k}^{6}{b}^{3}+{k}^{6}{b}^{4}+32\,\delta \,s\gamma \,{k} ^{4}ba+16\,a{k}^{4}s\delta \,{b}^{2}+64\,{a}^{2}{s}^{2}}}{8a}.} \end{array} \right\} \end{aligned}$$
(37)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{5.1}(x,t)=-\,{\frac{5k\left( 2\,\gamma +b\right) }{2a}}-6\,k\left( 2\,\gamma +b\right) \nonumber \\{} & {} \qquad \quad \frac{\left( 1\!+\!\cosh \left( {\frac{k{x}^{\beta }}{\beta } }\!+\!{\frac{w{t}^{\alpha }}{\alpha }}\right) \!+\Vert !\sinh \left( {\frac{k{x}^{\beta } }{\beta }}\!+\!{\frac{w{t}^{\alpha }}{\alpha }}\right) \right) }{{a}\left( \!-\!3-2\,\cosh \left( {\frac{k{x}^{\beta }}{\beta }}\!+\Vert !{\frac{w{t}^{\alpha }}{ \alpha }}\right) -2\,\sinh \left( {\frac{k{x}^{\beta }}{\beta }}\!+\!{\frac{w{t} ^{\alpha }}{\alpha }}\right) \right) }. \nonumber \\ \end{aligned}$$
(38)

Group 6: If the expressions given for \(\theta , p\) and \(\varphi \) in the Table 1 are used, we have

$$\begin{aligned}{} & {} \text {Set 6.1}:\nonumber \\{} & {} \left\{ {A_{0}}={\frac{k\left( 2\,\gamma +b\right) }{a}},{A_{1}}=0,{B_{1}}=\right. \nonumber \\{} & {} \left. -2\,{ \frac{k\left( 2\,\gamma +b\right) }{a}},\quad \delta ={\frac{2\,\gamma \,{k}^{3}wb+{k}^{3}w{b}^{2}-a{w}^{2}+a{s}^{2}}{{k} ^{4}\left( 2\,\gamma +b\right) bs}.} \right\} \nonumber \\ \end{aligned}$$
(39)

Therefore, the solution of (19) is given by

$$\begin{aligned}{} & {} u_{6.1}(x,t) ={\frac{k\left( b+2\,\gamma \right) }{a}} +4\,ik\left( b+2\,\gamma \right) \nonumber \\{} & {} \frac{\sin \left( \xi \right) }{{a}\left( \left( -1-i\right) \left( \cos \left( \xi \right) +i\sin \left( \xi \right) \right) +\left( 1-i\right) \left( \cos \left( \xi \right) -i\sin \left( \xi \right) \right) \right) }, \nonumber \\ \end{aligned}$$
(40)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned}{} & {} \text {Set 6.2}:\nonumber \\{} & {} \left\{ {A_{0}}=-{\frac{k\left( 2\,\gamma +b\right) }{a}},{ A_{1}}={\frac{k\left( 2\,\gamma +b\right) }{a}},{B_{1}}=0,\right. \nonumber \\{} & {} \qquad \qquad \left. \delta ={\frac{ 2\,\gamma \,{k}^{3}wb+{k}^{3}w{b}^{2}-a{w}^{2}+a{s}^{2}}{{k}^{4}\left( 2\,\gamma +b\right) bs}.}\right\} \end{aligned}$$
(41)

Therefore, the solution is

$$\begin{aligned}{} & {} u_{6.2}(x,t) =-{\frac{k\left( b+2\,\gamma \right) }{a}} +\,ik\left( b+2\,\gamma \right) \nonumber \\{} & {} \frac{\left( \left( -1-i\right) \left( \cos \left( {\xi }\right) \!+\!i\sin \left( {\xi }\right) \right) \!+\!\left( 1-i\right) \left( \cos \left( {\xi }\right) \!-\!i\sin \left( {\xi }\right) \right) \right) }{2{a}\sin \left( {\xi }\right) },\nonumber \\ \end{aligned}$$
(42)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

Group 7: If the corresponding function \(\varphi \) in the Table 1 for \(p=[2-i,2+i,1,1]\) and \(\theta =[i,-i,i,-i]\) is used, we get:

$$\begin{aligned}{} & {} \text {Set 7.1}:\nonumber \\{} & {} \left\{ \begin{array}{l} {A_{0}}=-2\,{\frac{k\left( 2\,\gamma +b\right) }{a}},{A_{1}}=0,{B_{1}}=5\,{ \frac{k\left( 2\,\gamma +b\right) }{a}}, \\ \\ w\!=\!{\frac{2\,{k}^{3}b\gamma \!+\!{k}^{3}{b}^{2}\!\pm \!\sqrt{4\,{\gamma }^{2}{k}^{6}{b} ^{2}\!+\!4\,\gamma {k}^{6}{b}^{3}\!+\!{k}^{6}{b}^{4}\!-\!4\,a{b}^{2}s\delta {k} ^{4}\!+\!4{a}^{2}{s}^{2}\!-\!8 a\gamma {k}^{4}\delta sb}}{2a}.}\!\!\! \end{array} \right\} \nonumber \\ \end{aligned}$$
(43)

The solution of (19) corresponding to these values is obtained as

$$\begin{aligned}{} & {} u_{7.1}(x,t) =-2\,{\frac{k\left( 2\,\gamma +b\right) }{a}} +10\,k\left( 2\,\gamma +b\right) \nonumber \\{} & {} \frac{\cos \left( {\xi }\right) }{{a} \left( \left( 2-i\right) \left( \cos \left( {\xi }\right) +i\sin \left( {\xi }\right) \right) +\left( 2+i\right) \left( \cos \left( {\xi }\right) -i\sin \left( {\xi }\right) \right) \right) },\nonumber \\ \end{aligned}$$
(44)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned}{} & {} \text {Set 7.2}:\nonumber \\{} & {} \left\{ \begin{array}{l} {A_{0}}=2\,{\frac{k\left( 2\,\gamma +b\right) }{a}},{A_{1}}=-{\frac{k\left( 2\,\gamma +b\right) }{a}},{B_{1}}=0, \\ \\ w\!=\!{\frac{2{k}^{3}b\gamma \!+\!{k}^{3}{b}^{2}\pm \sqrt{4{\gamma }^{2}{k}^{6}{b} ^{2}\!+\!4\gamma {k}^{6}{b}^{3}\!+\!{k}^{6}{b}^{4}\!-\!4\,a{b}^{2}s\delta {k} ^{4}\!+\!4{a}^{2}{s}^{2}-8\,a\gamma \,{k}^{4}\delta sb}}{2a}.} \end{array}\!\!\! \right\} \nonumber \\ \end{aligned}$$
(45)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{7.2}(x,t) =2\,{\frac{k\left( 2\,\gamma +b\right) }{a}} -\,k\left( 2\,\gamma +b\right) \nonumber \\{} & {} \frac{\left( \left( 2-i\right) \left( \cos \left( {\xi }\right) +i\sin \left( {\xi }\right) \right) +\left( 2+i\right) \left( \cos \left( {\xi }\right) -i\sin \left( {\xi }\right) \right) \right) }{2{a}\cos \left( {\xi }\right) },\nonumber \\ \end{aligned}$$
(46)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

Group 8: If the corresponding function \(\varphi \) in the Table 1 for \(p=[2,0,1,-1]\) and \(\theta =[1,0,1,-1]\) is used, we get:

$$\begin{aligned}{} & {} \text {Set 8.1}:\nonumber \\{} & {} \left\{ \begin{array}{c} {A_{0}}=-{\frac{\left( 2\,\gamma +b\right) k}{a}},{A_{1}}={\frac{\left( 2\,\gamma +b\right) k}{a}},{B_{1}}=0, \\ \\ w\!=\!{\frac{-\!2\gamma {k}^{3}b\!-\!{k}^{3}{b}^{2}\!\pm \!\sqrt{4{b}^{2}{k}^{6}{ \gamma }^{2}\!+\!4{b}^{3}{k}^{6}\gamma \!+\!{k}^{6}{b}^{4}\!+\!4{a}^{2}{s} ^{2}\!+\!8 a\delta s\gamma {k}^{4}b\!+\!4 a\delta s{b}^{2}{k}^{4}}}{2a}.} \end{array}\!\! \right\} \nonumber \\ \end{aligned}$$
(47)

The solution of (19) corresponding to these values is given by

$$\begin{aligned}{} & {} u_{8.1}(x,t)=-{\frac{\left( 2\,\gamma +b\right) k}{a}}\nonumber \\{} & {} +\left( 2\,\gamma +b\right) k\frac{\left( \cosh \left( {\frac{k{x}^{\beta }}{\beta }}+{\frac{w{ t}^{\alpha }}{\alpha }}\right) +\sinh \left( {\frac{k{x}^{\beta }}{\beta }}+{ \frac{w{t}^{\alpha }}{\alpha }}\right) \right) }{{a}\sinh \left( {\frac{k{x} ^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\right) }. \end{aligned}$$
(48)

6 Main outcomes of solving model Eq. (5) using IBSEFM

To apply the IBSEFM by considering the ODE (19), with the help of the balancing principle, we obtain the relationship between m, n and M as follows:

$$\begin{aligned} M+m=n+1. \end{aligned}$$
(49)

This equation yields \(M= 3,m = 1\) gives \(n = 3\). Consequently, the trial solution to Eq. (19) has the following form:

$$\begin{aligned} u(\zeta )=\frac{\sum _{i=0}^{3}a_iq^i}{\sum _{j=0}^{1}b_jq^j}=\frac{ a_0+a_1q+a_2q^2+a_3q^3}{b_0+b_1q}, \end{aligned}$$
(50)

where q demonstrates the improved Bernoulli equation solution (12).

$$\begin{aligned}{} & {} \text {Set 1}:\left\{ \begin{array}{c} {\ a_{0}}={\frac{{\ a_{1}}\,{\ b_{0}}}{{\ b_{1}}}},{\ a_{1}}={\ a_{1}},{\ a_{2}}={\frac{{\ a_{3}}\,{\ b_{0}}}{{\ b_{1}}}},{\ b_{0}}={\ b_{0}},k=\,{ \frac{{\ a_{3}}\,a}{2bA{\ b_{1}}}},\gamma =-b, \\ \\ w=-\,{\frac{{a}^{2}{\ a_{3}}\,{\ a_{1}}^{2}A-{a}^{2}{\ a_{3}}^{2}B{\ a_{1}}\pm \sqrt{16\,{\ b_{1}}^{6}{s}^{2}{A}^{4}{b}^{2}+{a}^{3}\left( {\ a_{1}}\,A-B{\ a_{3}}\right) {\ a_{1}}\,{\ a_{3}}^{2}\left( Aa{\ a_{1}}^{2}+4\,A{\ b_{1}} ^{2}\delta \,s-aB{\ a_{3}}\,{\ a_{1}}\right) }}{4{\ b_{1}}^{3}b{A}^{2}}.} \end{array} \right\} \end{aligned}$$
(51)

For \(A\ne B,\)

$$\begin{aligned}{} & {} u_{1}(x,t)={\frac{{\ a_{1}}\,{A}^{2}{{e}^{2\,B\xi }}-2\,{\ a_{1}}\,EBA+{\ a_{1}}\,{E}^{2}{B}^{2}{{e}^{-2\,B\xi }}-{\ a_{3}}\,A{{e}^{2\,B\xi }}B+{\ a_{3}}\,E{B}^{2}}{\left( A{{e}^{2\,B\xi }}-EB\right) {\ b_{1}}\,\left( A-E{{e }^{-2\,B\xi }}B\right) },} \end{aligned}$$
(52)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

For \(A=B,\)

$$\begin{aligned} u_{2}(x,t)=\frac{{\frac{{\ a_{1}}\,{\ b_{0}}}{{\ b_{1}}}}+{\ a_{1}}\left( \frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }\right) ^{-1/2}+{\frac{{\ a_{3}}\,{\ b_{0}}\,\left( 1+\tanh \left( A\xi \right) \right) }{{\ b_{1}}\,\left( E-1-\left( E+1\right) \tanh \left( A\xi \right) \right) }}+{\ a_{3}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-3/2}}{{\ b_{0} }+{\ b_{1}}{\ }\left( \frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }\right) ^{-1/2}}, \end{aligned}$$
(53)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned} \text {Set 2}:\left\{ \begin{array}{l} {\ a_{0}}=\,{\frac{B{\ a_{3}}\,{\ b_{0}}}{2A{\ b_{1}}}},{\ a_{1}}={\frac{B{\ a_{3}}}{2A}},{\ a_{2}}={\frac{{\ a_{3}}\,{\ b_{0}}}{{\ b_{1}}}},{\ b_{0}}={\ b_{0}},k=k, \\ w=\,{\frac{{k}^{2}b{B}^{2}{\ a_{3}}\pm \sqrt{{b}^{2}{k}^{4}{B}^{4}{\ a_{3}} ^{2}-8\,{\ b_{1}}\,A{\ a_{3}}\,\delta \,sb{k}^{3}{B}^{2}+16\,{\ b_{1}}^{2}{A} ^{2}{s}^{2}}}{4A{\ b_{1}}}},\gamma =-{\frac{2\,k{\ b_{1}}\,bA+{\ a_{3}}\,a}{4 {\ b_{1}}\,kA}.} \end{array} \right\} \end{aligned}$$
(54)

For \(A\ne B,\)

$$\begin{aligned} u_{3}(x,t)=-\,{\frac{\left( {A}^{2}{{e}^{2\,B\xi }}-{E}^{2}{B}^{2}{\ {e} ^{-2\,B\xi }}\right) B{\ a_{3}}}{2\left( A{{e}^{2\,B\xi }}-EB\right) {\ b_{1} }\,A\left( A-E{{e}^{-2\,B\xi }}B\right) },} \end{aligned}$$
(55)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

For \(A=B,\)

$$\begin{aligned}{} & {} u_{4}(x,t) \!=\!\left( 1/2\,{\frac{{a_{3}}\,{b_{0}}}{{b_{1}}}}\!+\!1/2\,{a_{3}}\! \left( {\frac{E\!-\!1\!-\!\left( E\!+\!1\right) \tanh \left( A\xi \right) }{1\!+\!\tanh \left( A\xi \right) }}\right) ^{-1/2}\right. \nonumber \\{} & {} \qquad \left. +{\frac{{a_{3}}\,{b_{0}}\,\left( 1+\tanh \left( A\xi \right) \right) }{{b_{1}}\,\left( E-1-\left( E+1\right) \tanh \left( A\xi \right) \right) }}\right. \nonumber \\{} & {} \qquad \left. +{a_{3}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-3/2}\right) \nonumber \\{} & {} \qquad \times \left( {b_{0}}+{b_{1}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}\right) ^{-1}, \end{aligned}$$
(56)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned} \text {Set 3}:\left\{ \begin{array}{c} {\ a_{0}}={\frac{{\ a_{3}}\,B{\ b_{0}}}{2{\ b_{1}}\,A}},{\ a_{1}}=\,{\frac{B{ \ a_{3}}}{2A}},{\ a_{2}}={\frac{{\ b_{0}}\,{\ a_{3}}}{{\ b_{1}}}},{\ b_{0}}={ \ b_{0}},k=\,{\frac{{\ a_{3}}\,a}{6Ab{\ b_{1}}}}, \\ \\ w={\frac{{B}^{2}{\ a_{3}}^{3}{a}^{2}\pm \sqrt{{B}^{4}{\ a_{3}}^{6}{a} ^{4}+20736\,{A}^{6}{\ b_{1}}^{6}{s}^{2}{b}^{2}-48\,{A}^{2}{\ b_{1}}^{2}{a} ^{3}{\ a_{3}}^{4}\delta \,s{B}^{2}}}{144{A}^{3}{\ b_{1}}^{3}b}},\gamma =-2\,b. \end{array} \right\} \end{aligned}$$
(57)

For \(A\ne B,\)

$$\begin{aligned}{} & {} u_{5}(x,t)\nonumber \\{} & {} =\,\frac{-B{\ a_{3}}\left( {{e}^{{\frac{B\left( 12\,w{t}^{\alpha }{ \ b_{1}}\,bA\beta +{\ a_{3}}\,a{x}^{\beta }\alpha \right) }{3{\ b_{1}} \,bA\beta \,\alpha }}}}{A}^{2}-{{e}^{-\,{\frac{B{\ a_{3}}\,a{x}^{\beta }}{3{ \ b_{1}}\,bA\beta }}}}{E}^{2}{B}^{2}\right) }{2{b_{1}A}\left( A{{e}^{\,{ \frac{B\left( {\ a_{3}}\,a{x}^{\beta }\alpha \!+\!6\,w{t}^{\alpha }{\ b_{1}} \,bA\beta \right) }{{\ 3b_{1}}\,bA\beta \,\alpha }}}}\!-\!EB\right) \left( A{{e} ^{\,{\frac{2Bw{t}^{\alpha }}{\alpha }}}}-E{{e}^{-\,{\frac{B{\ a_{3}}\,a{x} ^{\beta }}{{\ 3b_{1}}\,bA\beta }}}}B\right) }.{\ }\nonumber \\ \end{aligned}$$
(58)

For \(A=B\),

$$\begin{aligned}{} & {} u_{6}(x,t) =\left( \,{\frac{{b_{0}}\,{a_{3}}}{2{b_{1}}}}+1/2\,{a_{3}} \left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}\right. \nonumber \\{} & {} \left. +{\frac{{b_{0}}\,{a_{3}}\,\left( 1+\tanh \left( A\xi \right) \right) }{{b_{1}}\,\left( E-1-\left( E+1\right) \tanh \left( A\xi \right) \right) }}\right. \nonumber \\{} & {} \left. +{a_{3}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-3/2}\right) \nonumber \\{} & {} \times \left( {b_{0}}+{b_{1}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}\right) ^{-1} \end{aligned}$$
(59)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned} \text {Set 4}:\left\{ \begin{array}{c} {\ a_{0}}=-\frac{{a_{3}}}{8}\,{B}^{2}\sqrt{\frac{-4A}{B}}{A}^{-2},{\ a_{1}} =\,{\frac{B{\ a_{3}}}{2A}},{\ a_{2}}=\sqrt{-\,{\frac{B}{4A}}}{\ a_{3}},{\ b_{0}}=\sqrt{-{\frac{B}{4A}}}{\ b_{1}},k=\,{\frac{{\ a_{3}}\,a}{6Ab{\ b_{1}}} } \\ \\ ,w={\frac{1}{144}}\,{\frac{{B}^{2}{\ a_{3}}^{3}{a}^{2}\pm \sqrt{{B}^{4}{\ a_{3}} ^{6}{a}^{4}+20736\,{A}^{6}{\ b_{1}}^{6}{s}^{2}{b}^{2}-48\,{A}^{2}{\ b_{1}} ^{2}{a}^{3}{\ a_{3}}^{4}\delta \,s{B}^{2}}}{{A}^{3}{\ b_{1}}^{3}b}},\gamma =-2\,b. \end{array} \right\} \end{aligned}$$
(60)

For \(A\ne B,\)

$$\begin{aligned} u_{7}(x,t)=-\,\frac{B{\ a_{3}}}{2}\,\sqrt{-\frac{A}{B}}\frac{\left( -B\sqrt{- \frac{1}{B}\left( A-BEe^{-2B\xi }\right) }\left( A^{2}e^{2B\xi }-B^{2}E^{2}e^{-2B\xi }\right) +2A\sqrt{-\frac{1}{A}B}\left( A^{2}e^{2B\xi }-B^{2}E^{2}e^{-2B\xi }\right) \right) }{\left( A-E{{e} ^{-2\,B\xi }}B\right) {A}^{2}\left( A{{e}^{2\,B\xi }}-EB\right) {\ b_{1}} \left( \sqrt{-{\frac{B}{A}}}\sqrt{-{\frac{A-E{{e}^{-2\,B\xi }}B}{B}}} +2\right) }, \end{aligned}$$
(61)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

For \(A=B\),

$$\begin{aligned}{} & {} u_{8}(x,t) =\left( \frac{i{\ a_{3}}\,}{4}+\,{\ }\frac{{a_{3}}}{2}\left( { \frac{-1-\left( E+1\right) \tanh \left( A\xi \right) +E }{1+\tanh \left( A\xi \right) }}\right) ^{-\frac{1}{2}}{\ }\right. \nonumber \\{} & {} \qquad \left. +\frac{{a_{3}}}{2}{\frac{\,i{\ }\,\left( 1+\tanh \left( A\xi \right) \right) }{E-1-\left( E+1\right) \tanh \left( A\xi \right) }}\right. \nonumber \\{} & {} \qquad \left. +{\ a_{3} }\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-3/2}\right) \nonumber \\{} & {} \qquad \times \left( \frac{i}{2}{\ b_{1}}+{\ b_{1}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}{\ }\right) ^{-1},\nonumber \\ \end{aligned}$$
(62)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

$$\begin{aligned} \text {Set 5}:\left\{ \begin{array}{c} {\ a_{0}}={\frac{{\ a_{3}}\,B{\ b_{0}}}{{\ 2b_{1}}\,A}},{\ a_{1}}={\frac{{\ a_{3}}\,B}{2A}},{\ a_{2}}={\frac{{\ b_{0}}\,{\ a_{3}}}{{\ b_{1}}}},{\ b_{0}}= {\ b_{0}},k={\frac{3{\ a_{3}}\,a}{2{\ b_{1}}\,bA}}, \\ \\ w=\,{\frac{9\,{B}^{2}{\ a_{3}}^{3}{a}^{2}\pm \sqrt{81\,{B}^{4}{\ a_{3}}^{6}{a} ^{4}+256\,{A}^{6}{\ b_{1}}^{6}{s}^{2}{b}^{2}-432\,{A}^{2}{\ b_{1}}^{2}{a}^{3} {\ a_{3}}^{4}\delta \,s{B}^{2}}}{16{A}^{3}{\ b_{1}}^{3}b}},\gamma =-\frac{2}{ 3}\,b. \end{array} \right\} \end{aligned}$$
(63)

For \(A\ne B,\)

$$\begin{aligned} u_{9}(x,t)=\frac{\,{\frac{{\ a_{3}}\,B{\ b_{0}}}{{\ 2b_{1}}\,A}}+\frac{{\ a_{3}}\,B}{2A}\left( -{\frac{A}{B}}+{\frac{E}{{{e}^{2\,B\xi }}}}\right) ^{-1/2}+{\ b_{0}}\,{\ a_{3}}{\ b_{1}}^{-1}\left( -{\frac{A}{B}}+{\ \frac{E}{{ {e}^{2\,B\xi }}}}\right) ^{-1}+{\ a_{3}}\left( -{\frac{A}{B}}+{\frac{E}{{{e} ^{2\,B\xi }}}}\right) ^{-3/2}}{{b_{0}}+{\ b_{1}}\left( -{\frac{A}{B}}+{\frac{ E}{{{e}^{2\,B\xi }}}}\right) ^{-1/2}}, \end{aligned}$$
(64)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

For \(A=B\),

$$\begin{aligned}{} & {} u_{10}(x,t) =\left( {\frac{{b_{0}}\,{a_{3}}}{2{b_{1}}}}+\,\frac{{a_{3}}}{2} \left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}\right. \nonumber \\{} & {} \qquad \left. +{\frac{{b_{0}}\,{a_{3}}\,\left( 1+\tanh \left( A\xi \right) \right) }{{b_{1}}\,\left( E-1-\left( E+1\right) \tanh \left( A\xi \right) \right) }}\right. \nonumber \\{} & {} \qquad \left. +{a_{3}}\left( {\frac{E-1-\left( E+1\right) \tanh \left( A\xi \right) }{1+\tanh \left( A\xi \right) }}\right) ^{-3/2}\right) \nonumber \\{} & {} \qquad \times \left( {b_{0}}+{b_{1}}\left( {\frac{-1-\left( E+1\right) \tanh \left( A\xi \right) +E }{1+\tanh \left( A\xi \right) }}\right) ^{-1/2}\right) ^{-1}, \end{aligned}$$
(65)

where \(\xi ={\frac{k{x}^{\beta }}{\beta }}+{\frac{w{t}^{\alpha }}{\alpha }}\).

7 Graphical analysis and discussions

The graphical analysis of solutions obtained for Eq. (5) is shown in Figs. 1, 2, 3, 4, 5, 6.

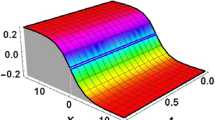
In Fig. 1, the solution (24) is shown graphically for different \(\alpha \) and \(\beta \) values. In Fig. 1a, the hyperbolic solution of (24) is plotted for integer order differential operators, i.e \(\alpha =1\) and \(\beta =1\). In Fig. 1b,c and d graphical representations are given for the increasing values of \(\alpha \) and \(\beta \). It has been observed that these graphs approach Fig. 1a as the values given to \(\alpha \) and \(\beta \) increase. The propagation of the foam for different values of the fractional orders are mapping continuously to the integer-order and preserving its physical shape.

Fig. 1
figure 1

3D-plot of (24) for \(A_1 = 0.5, a = 0.3, b =0.2, \delta = 3, \gamma = 0.1, s = 2 \) with a \(\beta =1\) and \( \alpha =1\)b \(\beta =0.05\) and \(\alpha =0.05\) c \(\beta =0.4\) and \(\alpha =0.4\). d \(\beta =0.9\) and \(\alpha =0.9\)

Full size image
Fig. 2
figure 2

Profiles of the solution (24) of left and right wave, respectively, for fixed \(\beta =0.5\) and varying \(\alpha \) over (0, 1]

Full size image
Fig. 3
figure 3

Profiles of the solution (24) of left and right wave, respectively, for fixed \(\alpha =0.9\) and varying \(\beta \) over (0, 1]

Full size image
Fig. 4
figure 4

3D-profiles of the solution (24) for \(\beta =1\) and \( \alpha =1\) with \(A_1 = 0.5, a = 0.3, b =0.2, \delta = 3, \gamma = 0.1\) for \(s=1,3,5\) respectively

Full size image
Fig. 5
figure 5

3D-plot of (52) for \(A = 1, B = 0.2, E = 1, a = -1, {a_1} = 20, {a_3} = 3, b = 1.3, {b_0} = - 0.3, {b_1} = 1, \delta = 1, s = 2\) with a \(\beta =1\) and \( \alpha =1\) b \(\beta =0.6\) and \(\alpha =0.5\) c \(\beta =0.9\) and \(\alpha =0.9\). d \(\beta =0.99\) and \( \alpha =0.99\)

Full size image
Fig. 6
figure 6

3D-plot of (64) for \(A = 1, B = 0.2, E = 1, a = -1, {a_1} = 20, {a_3} = 3, b = 1.3, {b _0} = - 0.3, {b _1} = 1, \delta = 0.85, s = 2 \) with a \(\beta =1\) and \( \alpha =1\) b \(\beta =0.1\) and \(\alpha =0.1\) c \( \beta =0.5\) and \(\alpha =0.5\). d \(\beta =0.999\) and \(\alpha =0.999\)

Full size image

Figure 2 demonstrates the profiles of the solution \(u_{1.2}\) (24) for \(x=1\) and for \(\beta \), which is considered constant, and \(\alpha \), which takes different values over (0, 1]. While Fig. 2a represents the left wave of (24), Fig. 2b represents the right wave of (24). As can be clearly seen from Set 1.2, there are two instantaneous values of wave speed w. In order to examine these two waves, they are called left wave and right wave. It is natural to accept these solutions as convergent series solutions for the integer order derivative solution. Moreover, the reflexive relation of these two-wave solutions are still attained in the presence of the \(\alpha \)-fractional derivative.

Figure 3 demonstrates the behaviors of the solution \(u_{1.2}\) (24) for \(t=1\) and for \(\alpha \), which is considered constant, and \(\beta \), which takes different values over (0, 1]. While Fig. 3a represents the left wave of (24), Fig. 3b represents the right wave of (24). Similar to what was stated above, \(\beta \) plays the role of \(\alpha \) here in the context of generating the convergent series solution. However, it would not be correct to say anything about the relationship of these two-wave solutions. Thanks to this result, it can be said that the concept of two-mode solution is derived from the two obtained different values of the wave speed w, which is basically the coefficient of the time coordinate. Therefore, the reflection property is not valid under the influence of changing the fractional order \(\beta \) of the space variable and fixing \(\alpha \).

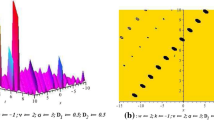
In Fig. 4, the general propagation of the kink-type solution (24) for \(\alpha =1\) and \(\beta =1\) is presented.Kink waves are travelling waves which rise or descend from one asymptotic state to another [72]. Figure 4 shows the relationship between the interaction angle of the kink-type left-right waves and their phase velocity s. It can be seen that as s increases, the interaction angle of the two waves decreases.

Table 2 Comparison of solutions
Full size table

In Fig. 5, the solution (52) is shown graphically for different \(\alpha \) and \(\beta \) values. Figure 5a was drawn for integer order differential operator, i.e \(\alpha =1\) and \(\beta =1\). This solution behaves as dark-bright wave. A combination of dark and bright solitons makes dark-bright solitons. A bright soliton is defined as a local surface soliton which transiently raises its wave amplitude. The dark soliton is characterized as a localized intensity dip below a continuous wave background. The changing in phase and amplitude component can be observed as the value of \(\alpha \) and \(\beta \) changes from Fig. 5. In Fig. 5b,c and d graphical representations are given for the increasing values of \(\alpha \) and \(\beta \). It has been observed that these graphs approach 5a as the values given to \(\alpha \) and \(\beta \) increase.

In Fig. 6, the solution (64) is shown graphically for different \(\alpha \) and \(\beta \) values. Figure 6a represents singular wave profile of (64) and was drawn for integer order differential operator, i.e \(\alpha =1\) and \(\beta =1\). In Fig. 6b,c and d graphical representations are given for the increasing values of \(\alpha \) and \(\beta \). The change in amplitude with respect to \(\alpha \) and \(\beta \) can be clearly seen in Fig. 5. It has been observed that these graphs approach 6a as the values given to \(\alpha \) and \(\beta \) increase. It reveals the effect of variation of fractional-order terms graphically on the solutions. The graphs have a great impact on explaining the physical behavior and the propagation and interactions of waves for the constructed solutions via choosing the appropriate values of the parameters.

To the best of our knowledge, this is the first time that an investigation for the conformable space-time two-mode foam drainage equation is reported in this study. If we consider the equation we address in this study in a more specialized form, it is possible to make some comparisons with existing studies. In [63], Alquran et al. consider two-mode version of the foam drainage Eq. (4) and apply updated rational sine-cosine and updated rational sinh-cosh methods to obtain solutions. In this paper, \(\beta \) and \(\alpha \) in (5) denote the conformable derivative orders of space and time, respectively. When \(\alpha =\beta =1\), Eq. (5) is known as the the foam drainage equation in two mode. As a result of comparing the existing solutions with the solutions we obtained, it is seen that in this study, if \(\beta \) and \(\alpha \) are integers, we obtained a larger number and type of solutions than obtained in [63]. In addition, the model considered is more comprehensive than the forms of this equation studied in the literature in the case of \(\alpha =\beta =1\). This shows that the methods used are effective in obtaining more comprehensive solutions.

In [61], the space-time fractional foam drainage Eq. (4) and used the modified Kudryashov method to get solutions. We note that in the case of \(s=0\) in (5), and integrate once with respect to the time variable t, we get Eq. (3). We observe that the derived solution \(u_{4.1}\) of Eq. (5) are similar to the solution (22) in [61]. A comparison between existing solutions and our obtained solutions is presented in Table 2. The others solution attain in this study are completely new and innovative and also have not reported in the prior study. It can be concluded from here that the methods used in this paper are very effective both in obtaining existing solutions in the literature and in reaching new solutions.

8 Concluding remarks

The two-mode foam drainage model equation appears in the field of industry and many applications where foam is mainly used as a basic and important material in the manufacturing of many tools and industries to be carried out in various fields such as liquid flow waves between bubbles, shallow water waves, capillary waves, electrohydro-dynamic model, ion acoustic plasma waves, etc.

This model (4) was proposed for the first time in [63]. In this study, conformable space-time derivatives have been taken into account for the relevant model. The conformable space-time two-mode foam drainage equation have been recommended to investigate the wave solutions by imposing the GERFM and the IBSEFM in this work. As a result, many solutions have been successfully built. To our best knowledge, the results obtained are reported for the first time. For the obtained solutions, the values of the relevant free parameters were selected appropriately and 3D graphics were drawn to make their physical appearance visible. Moreover, with the 2D graphs drawn, the reflexive property for the two-mode solution concept was examined if the time and space derivatives were kept constant, respectively. Our comprehensive analysis, including exact solutions and calculations, highlighted the simplicity, consistency and effectiveness of the techniques used. Due to the applications of the foam drainage equation in many fields including many scientific and engineering such as foods, personal care products, cleaning and scrubbing of clothes, chemical and material science and firefighting industries, we hope that the results obtained in this study will contribute to this field. Solutions to the foam drainage equation play a key role in elucidating the dynamics of foam behavior, with a profound impact on a wide range of potential applications across industries. By providing insight into foam stability, drainage kinetics and the influence of additives, these solutions guide the optimization of manufacturing processes and the formulation of products in sectors such as food production, oil recovery, personal care and materials science. Understanding how different parameters affect foam properties enables the development of tailored solutions for specific applications, ranging from the creation of stable food foams to the design of lightweight materials and advanced drug delivery systems. By applying foam drainage equation solutions, researchers can not only improve product performance and process efficiency, but also drive innovation in diverse fields by exploiting the unique properties of foam structures. Additionally, further research may be conducted in the future using definitions of fractional derivatives using different methodologies, and it is planned that the methodologies presented in this paper will be extended to model physical problems in science and engineering.