1 Introduction

Stability of structures under conservative and non-conservative loads is a classical problem [1,2,3], with interesting aspects from theoretical and practical perspectives. Examples include jet or rocked propelled aerospace vehicles [4,5,6,7], elastic systems in presence of dry friction [8,9,10], piezoelectric beams [11,12,13,14], as well as fluid conveying pipes and other structures that interact with a fluid flow [15,16,17]. In many cases, damping is of the external type, e.g., it is associated with the interaction of the system with an external fluid [18]. However, damping can also manifest itself as an internal cause, due to material dissipation, as, e.g., that ruled by the rheological Kelvin-Voigt damping model [19,20,21,22]. The effects of damping on the stability of non-conservative systems, as, for example, those loaded by non-conservative forces of positional type, such as follower forces [9, 23, 24], are sometime unexpected by intuition. In this framework, the well-known damping destabilization paradox or, said in other words, the destabilizing effect of internal damping [20, 21, 25] manifests itself through the finite reduction of the critical load of circulatory systems (i.e., undamped systems loaded by non-conservative positional forces) when they are perturbed by small damping [26]. A paradigmatic discrete system exhibiting this phenomenon is the Ziegler’s double pendulum [2, 21, 27, 28], while a continuous one is the Beck’s column, i.e., an unshearable, inextensible visco-elastic cantilever beam loaded by a follower force at the free end [1, 27, 29,30,31].

Systems such as those mentioned above have been widely studied in the literature, in both linear and nonlinear fields [30,31,32,33,34,35,36,37,38,39]. In particular, in [32] the nonlinear response of a cantilever planar beam in the presence of lateral excitations and support motion is addressed, while the nonlinear flexural-flexural oscillations of the beam under lateral excitations are studied in [33]. Flutter and divergence instabilities of vertical columns subjected to follower actions (like those produced by a jet engine) are investigated in [40, 41]. Follower actions can also be generated by dry friction, as is discussed in [9, 42, 43], where the results of theoretical and experimental investigations concerning the loss of stability of slender elastic elements induced by dry friction is addressed. The stability of a double pendulum subjected to follower and dead forces, with specific attention to chaotic motions, is addressed in [39]. In [34,35,36] the critical and post-critical bifurcation scenarios of a Beck’s column are investigated via the Method of Multiple Scales, revealing divergence, Hopf’s, and double-zero bifurcations. In [30] the complex bifurcation scenarios, taking place in a Beck’s column under the combination of conservative and non-conservative loads is discussed. In [31] the nonlinear dynamics close to a Hopf’s bifurcation is investigated, and the so-called Hard Loss of Stability of a Ziegler’s double pendulum and of a Beck’s column, in the presence of a Van-der-Pole-like internal damping (see also [44]) is detected. The nonlinear behavior of both systems has been found to be qualitative the same and the Hard Loss of stability has also been studied analytically for the first system. The simultaneous presence of internal and external damping forms, although of the linear type only, has been considered in [30, 37, 38] among the others. In [13, 14, 45, 46] the use of distributed piezoelectric devices is also explored with the aim to improve the stability of a Beck’s column subjected to linear damping actions of the internal and external types.

The aforementioned works have addressed several aspects of the linear and nonlinear dynamics of discrete and continuous systems, including bifurcation phenomena. However, a targeted investigation on the nonlinear dynamic behavior of continuous one-dimensional systems under the action of conservative and non-conservative loads, and in the presence of combined and complex damping forms as due to material behavior (internal damping) and to fluid–structure interactions (external damping), seems to be missing in the current literature on the subject.

The present paper is framed in the above-mentioned scenario and aims to shed the light on the role played by different (internal and external) nonlinear damping forms on the complex dynamics of nonlinear systems subjected to conservative and non-conservative loads. The paradigmatic system, here considered to perform this investigation, is a generalized Beck’s column made of a nonlinear visco-elastic material, and subjected to nonlinear dissipative loads distributed along its length, plus conservative and non-conservative forces applied at its free end. A variational principle provides the equations of motion of the system, which are properly recast into an integro-differential form. The linear stability analysis of the system is then carried out and bifurcation points are detected in the space of parameters associated with the loads applied at the free end. Starting from Hopf’s bifurcation points, a post-critical analysis, based on the Method of Multiple Scales [30, 47,48,49], is directly performed on the continuous system to analytically study the combined influence of the internal and external nonlinear damping forms. One of the main findings is that both forms of nonlinear damping can turn a supercritical instability of the system into a subcritical one, thus revealing another destabilizing effect of damping, occurring in the nonlinear field, beyond the very well-known one, already mentioned in the foregoing. Comparisons with the results of a numerical approach, grounded on a Galerkin discretization of the original system, are also illustrated and confirm the analytical findings of the present study.

Fig. 1
figure 1

Generalized Beck’s column made of a nonlinear visco-elastic material and embedded in a nonlinear transverse dissipative field

Full size image

The paper is organized as follows. The mechanical model is introduced in Sect. 2. The linear stability analysis of the system is recalled in Sect. 3, while in Sect. 4 the Multiple Scales Method (MSM) is applied and the relevant bifurcation equations obtained and discussed. Numerical examples are developed in Sect. 5, to check the analytical findings. Finally, conclusions are drawn and possible prospects are illustrated in Sect. 6.

2 Mechanical model

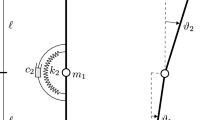
Let us consider the planar structure represented in Fig. 1. It will be referred to as the generalized visco-elastic Beck’s column (see, e.g., [1, 12, 19, 30]), namely, an unshearable, inextensible and visco-elastic cantilever beam, of length l, mass per unit length m, and bending stiffness EI, where E is the elastic modulus and I is the cross-section moment of inertia. It is subject to the combination of a dead (conservative) force, P, and a follower (non-conservative) force, F, applied at its free end (point B in the beam reference configuration). The variable \(s\in [0,l]\) is taken as a material abscissa, spanning the points of the beam axis-line, and \(t\in [0,+\infty )\) is the time.

The beam is made of a nonlinear visco-elastic material, belonging to a class of rheological models including Kelvin-Voigt-, Van der Pol- and Rayleigh-type constitutive laws; this dissipation is referred to as nonlinear internal damping (since it is due to material properties of the system) and is modelled by the function D(s, t). Moreover, nonlinear interactions of the beam with the external environment are assumed to be exerted by a distribution of transverse nonlinear dashpots, located along the whole beam length, whose external dissipative effect is denoted by the function b(s, t). The system reduces to the classical Beck’s column [1] when the dead force, P, the nonlinear external damping, b, and the nonlinear internal damping, D, vanish.

The beam model is formulated as a one-dimensional polar continuum, made of a deformable axis-line and of rigid cross-sections which are normal to the straight axis-line in the reference configuration [50]. The beam lies in the plane of normal \(\bar{\textbf{a}}_{z}\) spanned by the unit-vectors \(\bar{\textbf{a}}_{x},\bar{\textbf{a}}_{y}\). The rotation \(\theta (s,t)\), about \(\bar{\textbf{a}}_{z}\), undergone by the material point \(\text {P}\) at the abscissa s and time t, transforms the local reference basis \(\bar{\mathcal {B}}\mathrel {\mathop {:}}=(\bar{\textbf{a}}_{x},\bar{\textbf{a}}_{y},\bar{\textbf{a}}_{z})\) attached to \(\text {P}^*\) into the local current basis \({\mathcal {B}}\mathrel {\mathop {:}}=({\textbf{a}}_{x}(s,t),{\textbf{a}}_{y}(s,t),{\textbf{a}}_{z}(s,t))\). Since the beam is unshearable, \({\textbf{a}}_{x}(s,t)\) is tangent to the axis-line. By enforcing the internal constraints of inextensibility and unshearability, the only strain measure is the beam curvature, which is defined as follows:

$$\begin{aligned} \kappa (s,t)=\theta ^{\prime }(s,t), \end{aligned}$$
(1)

where the prime denotes differentiation with respect to s. Moreover, the following kinematics relations hold:

$$\begin{aligned} \begin{array}{l} v^{\prime }(s,t) = \sin (\theta (s,t)) , \\ u^{\prime }(s,t) = \cos (\theta (s,t)) -1 , \end{array} \end{aligned}$$
(2)

where u(s, t) and v(s, t) are scalar fields describing the longitudinal and transverse displacements of the beam axis, respectively, which, together with \(\theta (s,t)\), must vanish at \(s=0\) (geometric boundary conditions), i.e.,

$$\begin{aligned} \begin{array}{l} u(0,t) = 0, \\ v(0,t) = 0,\\ \theta (0,t)=0. \end{array} \end{aligned}$$
(3)

Here the deflection v(s, t) is taken as the kinematic descriptor (accordingly, the formulation is referred to as the v-formulation). To this end u(s, t) and \(\theta (s,t)\) are written as functions of v(s, t). From Eq. (2)-a, it is

$$\begin{aligned} \theta \left( s,t\right) =\arcsin \left( v'\left( s,t\right) \right) , \end{aligned}$$
(4)

which, substituted in Eq. (2)-b, after space integration, furnishes

$$\begin{aligned} \begin{aligned}&u(s,t)=\int _{0}^{s}\left( \cos \left( \theta ({\hat{s}},t)\right) -1\right) \,\textrm{d}{\hat{s}},\end{aligned} \end{aligned}$$
(5)

where use is made of Eq. (3)-a.

The equations of motion of the generalized Beck’s column in Fig. 1 are derived by using the extended Hamilton’s principle, according to which the following variational condition has to be satisfied

$$\begin{aligned} \delta \mathcal {H} = 0 , \end{aligned}$$
(6)

for any kinematically admissible motion of the system, where \(\delta \mathcal {H}\) denotes the first variation of the action functional and is defined in “Appendix A”.

Following the procedure reported in “Appendix A”, a single integro-differential equation in the unknown function v(s, t) is obtained, namely:

$$\begin{aligned}&- m \ddot{v}(s,t) + p(s,t) \nonumber \\&+ \bigg [ \frac{v^{\prime }(s,t) \big (H(l,t) {-} \int _{s}^{l} m \ddot{u}(x,t) \big ) {-} M^{\prime }(s,t)}{1+u^{\prime }(s,t)} \bigg ]^{\prime } = 0, \, \end{aligned}$$
(7)

with natural boundary conditions

$$\begin{aligned} \begin{array}{l} M(l,t)=0, \, \\ M^{\prime }(l,t) + P v^{\prime }(l,t) = 0. \, \end{array} \end{aligned}$$
(8)

In (7)–(8), the overdot denotes differentiation with respect to time t, M(s, t) is the internal bending moment at the cross-section s at the time t, p(s, t) is the vertical external load distributed along the beam length (in the problem at hand, it coincides with the distributed dissipative external actions), and, finally, H(l, t) represents the horizontal component of the total tip force in the actual configuration of the beam, i.e., \(H(l,t) = -P -F \cos (\theta (l,t))\).

The constitutive law for the bending moment is assumed to be ruled by the linear visco-elastic Kelvin-Voigt model, coupled with a nonlinear hysteretic dashpot, which is ruled by a Van-der-Pol- and Rayleigh-like law; it reads:

$$\begin{aligned} M(s,t) = EI \, \kappa (s,t) + D(s,t)I \, {\dot{\kappa }}(s,t), \, \end{aligned}$$
(9)

where the nonlinear internal damping function D(s, t) is defined by

$$\begin{aligned} D(s,t) = d_0 + d_1 \kappa ^2(s,t) + d_2 {\dot{\kappa }}^2(s,t), \, \end{aligned}$$
(10)

with \(d_0\), \(d_1\), and \(d_2\) prescribed material constants.

The distributed external load p(s, t) is expressed in the form

$$\begin{aligned} p(s,t) = - b(s,t) \, {\dot{v}}(s,t), \, \end{aligned}$$
(11)

where the nonlinear external damping function b(s, t) is given by

$$\begin{aligned} b(s,t) = b_0 + b_1 v^2(s,t) + b_2 {\dot{v}}^2(s,t), \, \end{aligned}$$
(12)

with \(b_0\), \(b_1\), and \(b_2\) prescribed constants that describe the constitutive behavior of the external medium that interacts with the beam.

In the following, the dependence of functions, e.g., v(s, t), on the independent variables s and t is understood and, hence, omitted. Moreover, the non-dimensional variables \({\tilde{t}} = \omega \, t\), \({\tilde{s}} = s/l\), and \({\tilde{v}} = v/l\) are introduced to recast the problem into a non-dimensional form, with \(\omega = \sqrt{m l^4 / EI}\).

By using (2) to express u and \(\theta \) in terms of v and expanding in Taylor’s series all equations up to cubic terms, the non-dimensional equation of motion and boundary conditions turn out to be (omitting the tilde)

$$\begin{aligned} \begin{aligned}&\ddot{v} + v^{\prime \prime \prime \prime } + 2(\mu +\nu ) v^{\prime \prime } + \alpha _0 {\dot{v}}^{\prime \prime \prime \prime } + \beta _0 {\dot{v}} +\\&\alpha _1 ({\dot{v}}^{\prime \prime } v^{\prime \prime \, 2})^{\prime \prime } + \alpha _2 ({\dot{v}}^{\prime \prime \, 3})^{\prime \prime } + \beta _1 {\dot{v}} v^2 + \beta _2 {\dot{v}}^3 + f = 0, \, \\&v_A = 0, \, \\&v_A^{\prime } = 0, \, \\&v_B^{\prime \prime } + \alpha _0 {\dot{v}}_B^{\prime \prime } + \alpha _1 {\dot{v}}_B^{\prime \prime } v_B^{\prime \prime \, 2} + \alpha _2 {\dot{v}}_B^{\prime \prime \, 3} + g_B = 0, \, \\&-v_B^{\prime \prime \prime } - \alpha _0 {\dot{v}}_B^{\prime \prime \prime } - 2 \nu v_B^{\prime } - \alpha _1 ({\dot{v}}_B^{\prime \prime } v_B^{\prime \prime \, 2})^{\prime } \\&\quad - \alpha _2 ({\dot{v}}_B^{\prime \prime \, 3})^{\prime } - h_B = 0, \, \end{aligned} \end{aligned}$$
(13)

where subscripts A, B denote evaluation of functions at the abscissa of the relevant points of Fig. 1, while functions f, g, h are defined in “Appendix B”, along with the dimensionaless parameters associated with internal damping (\(\alpha _0\), \(\alpha _1\), \(\alpha _2\)), external damping (\(\beta _0\), \(\beta _1\), \(\beta _2\)), and tip loads (\(\mu \), \(\nu \)).

3 Linear stability analysis

To study the system dynamics it is first necessary to perform a linear stability analysis and identify eventual bifurcation points. This is followed by a bifurcation analysis to investigate the behavior of the nonlinear system close to a bifurcation point, i.e., in the so-called post-critical regime. The aim is to give an answer to the following questions: does the system tend to limit-cycles? is the post-critical behavior stable or not? what is the influence of nonlinear damping on the behavior of the system close to a bifurcation point? To answer to these questions an analytical approach, grounded on the Multiple Scales Method, is pursued in Sect. 4.1, while the linear stability and bifurcation analysis that precedes it is addressed hereafter.

A linear stability analysis calls for determining eigenvalues and eigenfunctions of the linear counterpart of problem (13), which reads:

$$\begin{aligned} \begin{array}{l} \ddot{v} + v^{\prime \prime \prime \prime } +2(\mu +\nu ) v^{\prime \prime } +\alpha _0 {\dot{v}}^{\prime \prime \prime \prime } + \beta _0 {\dot{v}} = 0, \, \\ v_A = 0, \, \\ v_A^{\prime } = 0, \, \\ v_B^{\prime \prime } + \alpha _0 {\dot{v}}_B^{\prime \prime } = 0, \, \\ -v_B^{\prime \prime \prime } - \alpha _0 {\dot{v}}_B^{\prime \prime \prime } - 2 \nu v_B^{\prime } = 0. \, \end{array} \end{aligned}$$
(14)

The linear problem (14) is not self-adjoint because of the follower (non-conservative) force associated with the dimensionless load parameter \(\mu \). Moreover, it coincides with a linear problem addressed in [19, 21, 30, 51]; see also [31], where the problem has been formulated in terms of the scalar field \(\theta \), instead of the more common transverse displacement v. In what follows, some well-known results of literature are recalled (see [30] for further details).

Stability of the trivial, rectilinear configuration of the generalized Beck’s column is governed by the linear eigenvalue problem (14). The space boundary value problem is obtained by taking \(v\left( s,t\right) =\phi \left( s\right) e^{\lambda t}\), and by substituting it in Eqs. (14), that becomes:

$$\begin{aligned} \begin{aligned}&\left( 1+\alpha _{0}\lambda \right) \phi ^{\prime \prime \prime \prime }+2\left( \mu +\nu \right) \phi ^{\prime \prime }+\left( \lambda ^{2}+\beta _{0}\lambda \right) \phi =0,\\&\phi (0)=0,\\&\phi ^{\prime }(0)=0,\\&\left( 1+\alpha _{0}\lambda \right) \phi ^{\prime \prime }(1)=0,\\&-\left( 1+\alpha _{0}\lambda \right) \phi ^{\prime \prime \prime }(1)-2\nu \phi ^{\prime }(1)=0.\\ \end{aligned} \end{aligned}$$
(15)

The field Eq. (15)-a and the boundary conditions at the clamp A, Eqs. (15)-b,c, lead to the solution:

$$\begin{aligned} \phi \left( s\right)= & {} C_{1}\left[ \cos (ps)-\cosh (qs)\right] \nonumber \\{} & {} +C_{2}\left[ \frac{\sin (ps)}{p}-\frac{\sinh (qs)}{q}\right] ,\, \end{aligned}$$
(16)

where \(p=p\left( \lambda ,\mu ,\nu ,\alpha _{0},\beta _{0}\right) \) \(\in {\mathbb {C}}\) and \(q=q\left( \lambda ,\mu ,\nu ,\alpha _{0},\beta _{0}\right) \) \(\in {\mathbb {C}}\). By enforcing the remaining boundary conditions at the tip B, an algebraic system is obtained, namely:

$$\begin{aligned} \textbf{S}_{\lambda }\textbf{c}=\textbf{0}, \, \end{aligned}$$
(17)

where \(\textbf{c}:=\left( C_{1},C_{2}\right) ^{T}\) is a vector of arbitrary (yet interdependent) constants, and \(\textbf{S}_{\lambda }\) is the “dynamic stiffness matrix” of the problem, function of the eigenvalue \(\lambda \), of the load parameters \(\mu \) and \(\nu \), and of the linear damping parameters \(\alpha _{0}\) and \(\beta _{0}\), i.e., \(\textbf{S}_{\lambda }=\textbf{S}_{\lambda }(\lambda ,\mu ,\nu ,\alpha _{0},\beta _{0})\). The characteristic equation,

$$\begin{aligned} \det \textbf{S}_{\lambda }=0, \, \end{aligned}$$
(18)

furnishes the eigenvalue of the system, \(\lambda =\lambda \left( \mu ,\nu ,\alpha _{0},\right. \)\(\left. \beta _{0}\right) \), for a given set of parameters, \(\mu ,\nu ,\alpha _{0},\beta _{0}\), while the solution of the (singular) system (17), for a given eigenvalue \(\lambda \), under a proper normalization condition, provides the associated eigenfunction (16).

A deep study of Eq. (18) has been carried out in [30], where the exact stability diagram for the generalized Beck’s column has been found. A sketch of the linear stability diagram is depicted in Fig. 2-a in the \((\nu ,\mu )\)-plane, for the undamped system, i.e., when \(\alpha _0=\beta _0=0\), and for three damped systems, referred to as (I) \(\alpha _0=0.001\), \(\beta _0=1\), (II) \(\alpha _0=0.01\), \(\beta _0=1\), and (III) \(\alpha _0=0.01\), \(\beta _0=10\). It is important to remark that only the lowest bifurcation branches, among the infinite ones, are shown.

Fig. 2
figure 2

Linear stability diagram of the generalized Beck’s column: a view of the stability chart in the \((\nu ,\mu )\)-plane, for an undamped system (\(\alpha _0=0, \, \beta _0=0\)) and three damped systems (I, II, III); b critical manifolds in the \((\mu ,\alpha _0,\beta _0)\)-parameter space for \(\nu =0\)

Full size image

It is found in [30] that the stable zone (shaded region in Fig. 2-a) is bounded by a divergence locus, \(\mathcal {D}\), which is a damping-independent curve describing a family of systems having (at least) one zero eigenvalue, and by a Hopf’s locus, which is a damping-dependent curve describing a family of systems having (at least) one complex conjugate eigenvalue pair with zero real part. In this respect, it is important to remark that when the damping is zero a “circulatory” system is obtained, for which all eigenvalues are purely imaginary. In this case, a “circulatory” or “reversible” Hopf’s bifurcation (see, e.g., [19, 21, 30, 52]) takes place at the manifold of the parameter plane \(\mathcal {H}_c\) on which the first two eigenvalues, \(\lambda _j=\pm i\omega _j\) \((j=1,2)\), merge into a double eigenvalue, \(\lambda =\pm i\omega _c\), at a critical Hopf’s load, \(\mu _c=\mu _c(\nu )\). On the contrary, with damping included, the system is “circulatory” and “dissipative”. In this case the Hopf’s bifurcation takes place at the manifold \(\mathcal {H}_d\) of the parameter plane on which a stable complex conjugate eigenvalue pair (having the lowest frequency and negative real part) becomes purely imaginary, i.e., \(\lambda =\pm i\omega _d\) at \(\mu _d=\mu _d(\nu )\) (critical Hopf’s load), entailing the incipient loss of stability of the system. Figure 2-a also shows the intersections between:

  • \(\mathcal {H}_c\) and the \(\mu \)-axis, which is the Beck’s point \(B_c\simeq (0;10.02)\);

  • \(\mathcal {H}_d^{I}\), \(\mathcal {H}_d^{II}\), \(\mathcal {H}_d^{III}\) and the \(\mu \)-axis, referred to here as “visco-elastic Beck’s” points, \(B_{d}^I\simeq (0;9.98)\), \(B_{d}^{II}\simeq (0;8.89)\), \(B_{d}^{III}\simeq (0;12.59)\);

  • \(\mathcal {H}_c\) and \(\mathcal {D}\), which is the double-zero bifurcation point \(DZ_c\simeq (5.51;3.02)\);

  • \(\mathcal {H}_d^{I}\), \(\mathcal {H}_d^{II}\), \(\mathcal {H}_d^{III}\) and \(\mathcal {D}\), i.e., the damped double-zero bifurcation points \(DZ_{d}^I\simeq (5.4;3.06)\), \(DZ_{d}^{II}\simeq (4.3;3.2)\), \(DZ_{d}^{III}\simeq (5.3;3.07)\);

  • \(\mathcal {D}\) and the \(\nu \)-axis, which is the first Eulerian critical load \(E_1=(\pi ^2/8;0)\).

As anticipated before, the Hopf’s loci depend on the linear damping parameters, \(\alpha _0\) and \(\beta _0\). In this respect, some theoretical outcomes from the linear stability analysis, concerning the influence of linear damping on the Hopf’s critical load are well-known in the literature [19, 30]. In particular, small internal damping is known to have a detrimental effect on a circulatory system, while external damping is beneficial. In general, the influence of linear damping on the stability of a generalized Beck’s column can be summarized as follows:

  • for a given \(\beta _{0}\), a small \(\alpha _{0}\) entails \(\mu _{d}(\nu )<\mu _{c}(\nu )\);

  • the larger is \(\beta _{0}\), the lower is the destabilizing effect of \(\alpha _{0}\);

  • for a sufficiently large \(\alpha _{0}\), the destabilizing effect of internal damping vanishes, i.e., \(\mu _{d}(\nu )>\mu _{c}(\nu )\);

  • for a given \(\left( \alpha _{0},\beta _{0}\right) \), the critical load \(\mu _{d}(\nu )\) increases with \(\beta _{0}\), but it can also increase with \(\alpha _{0}\), providing it is sufficiently large.

In this framework, the critical manifold, which bonds the stable region of the system, also known in the literature as the “Whitney’s umbrella” surface [53, 54], is a hyper-surface in the \((\mu ,\nu , \alpha _0, \beta _0)\)-parameter space that can be conveniently represented by sections \(\nu =\mathrm const\). The manifold is represented in Fig. 2-b, when \(\nu =0\), by tackling directly Eq. (18) and by determining the combinations of load and damping parameters at which Hopf’s, divergence and double-zero bifurcations occur.

4 Nonlinear analysis

Following the lines of [30, 31], and focusing our attention on a class of damped systems (i.e., given the linear damping parameters), a post-critical analysis from a Hopf’s bifurcation point is carried out by using the Multiple Scales Method. This is applied in the so-called direct form, namely, directly on the integro-partial differential equations of motion and boundary conditions, thus avoiding any a-priori discretization of such equations. See, e.g., [55, 56].

The aim is to obtain an analytical asymptotic approximation of the system behavior, able to shed the light on the qualitative and quantitative influence of nonlinear damping of the internal and external type or, said in other words, the effect of the nonlinear damping parameters, \(\alpha _1\), \(\alpha _2\), \(\beta _1\), \(\beta _2\), on the nonlinear dynamics of the system and, in particular, on the presence of limit-cycles, their amplitude and stability.

It is worth to notice that, in what follows, a first-order Multiple Scales algorithm is developed, which is able to furnish bifurcation equations that govern the nonlinear dynamics of the (reduced) system close to the Hopf’s bifurcation. If the analysis is pushed up to the second-order, as done in [27] for the Ziegler’s double pendulum, it would permit the derivation of a more complete bifurcation equation and the study of more complex phenomena, such as the so-called Hard Loss of Stability observed for the Ziegler’s double pendulum. Phenomena of this kind are not in the scope of the present work and will be addressed in a subsequent investigation.

4.1 Bifurcation equations

Let us consider a damped system undergoing a Hopf’s bifurcation at the point \(\mu =\mu _d\), \(\nu =\nu _d\) of the load parameters domain, which is taken as the starting point for the asymptotic analysis. The first step of the method used here consists in the rescaling and expansion of the scalar field v(s, t), i.e., \(v \rightarrow \varepsilon ^{1/2} (v_0 + \varepsilon v_1 + \varepsilon ^2 v_2 +...)\), where \(0<\varepsilon \ll 1\) is a small bookkeeping parameter (to be reabsorbed at the end of the procedure). The load parameters are recast in the form \(\mu = \mu _d +\varepsilon \delta \mu \), \(\nu = \nu _d + \varepsilon \delta \nu \), where \(\delta \mu \) and \(\delta \nu \) represent small load increments measured from the bifurcation point. Subsequently, independent time scales are introduced, namely, \(t_k = \varepsilon ^k \, t\), \(k=0,1,...\), such that the total time derivative is expressed in the form \(\textrm{d}/\textrm{d}t = \textrm{d}_0 + \varepsilon \, \textrm{d}_1 + \varepsilon ^2 \, \textrm{d}_2 +...\), and \(\textrm{d}^2/\textrm{d}t^2 = \textrm{d}_0^2 + 2 \varepsilon \, \textrm{d}_0 \textrm{d}_1 + \varepsilon ^2 \, (\textrm{d}_1^2 + 2 \textrm{d}_0 \textrm{d}_2) +...\), where \(\textrm{d}_k\) stands for differentiation with respect to \(t_k\). Finally, perturbation equations are obtained by substitution in Eqs. (13) and collection of terms with the same power of \(\varepsilon \).

The perturbation equations of order \(\varepsilon ^0\) and \(\varepsilon ^1\) read:

$$\begin{aligned} \varepsilon ^0: \,\,\, {\left\{ \begin{array}{ll} \textrm{d}_0^2 v_0 + \beta _0 \textrm{d}_0 v_0 + \alpha _0 \textrm{d}_0 v_0^{\prime \prime \prime \prime } + v_0^{\prime \prime \prime \prime } \\ \quad + 2(\mu _d+\nu _d) v_0^{\prime \prime } = 0 , \\ v_{0A} = 0 , \\ v_{0A}^{\prime } = 0 , \\ v_{0B}^{\prime \prime } + \alpha _0 \textrm{d}_0 v_{0B}^{\prime \prime } = 0 , \\ -v_{0B}^{\prime \prime \prime } - \alpha _0 \textrm{d}_0 v_{0B}^{\prime \prime \prime } - 2 \nu _d v_{0B}^{\prime } = 0 , \end{array}\right. } \end{aligned}$$
(19)
$$\begin{aligned} \varepsilon ^1: \,\,\, {\left\{ \begin{array}{ll} \textrm{d}_0^2 v_1 + \beta _0 \textrm{d}_0 v_1 + \alpha _0 \textrm{d}_0 v_1^{\prime \prime \prime \prime } + v_1^{\prime \prime \prime \prime }\\ \quad + 2(\mu _d+\nu _d) v_1^{\prime \prime } + 2 \textrm{d}_1 \textrm{d}_0 v_0 + \\ \beta _0 \textrm{d}_1 v_0 + 2(\delta \mu + \delta \nu ) v_0^{\prime \prime } + \alpha _0 \textrm{d}_1 v_0^{\prime \prime \prime \prime } \\ \quad + \beta _1 v_0^2 \textrm{d}_0 v_0 + \beta _2 (\textrm{d}_0 v_0)^3 + \\ \alpha _1 ((v_0^{\prime \prime })^2 \textrm{d}_0 v_0)^{\prime \prime } + \alpha _2 ((\textrm{d}_0 v_0^{\prime \prime })^3) + {\tilde{f}}_0 = 0 , \\ v_{1A} = 0 , \\ v_{1A}^{\prime } = 0 , \\ v_{1B}^{\prime \prime } + \alpha _0 \textrm{d}_0 v_{1B}^{\prime \prime } + \alpha _0 \textrm{d}_1 v_{0B}^{\prime \prime } + \\ \alpha _1 ((v_{0B}^{\prime \prime })^2 \textrm{d}_0 v_{0B}) {+} \alpha _2 ((\textrm{d}_0 v_{0B}^{\prime \prime })^3) {+} {\tilde{g}}_{0B} = 0 , \\ -v_{1B}^{\prime \prime \prime } - \alpha _0 \textrm{d}_0 v_{1B}^{\prime \prime \prime } - 2 \nu _d v_{1B}^{\prime } - 2 \delta \nu v_{0B}^{\prime } \\ - \alpha _1 ((v_{0B}^{\prime \prime })^2 \textrm{d}_0 v_{0B})^{\prime } - \alpha _2 ((\textrm{d}_0 v_{0B}^{\prime \prime })^3)^{\prime }\\ \quad - {\tilde{h}}_{0B} = 0 , \end{array}\right. } \end{aligned}$$
(20)

where functions \({\tilde{f}}_0\), \({\tilde{g}}_0\) and \({\tilde{h}}_0\), which collect cubic terms, are defined as:

$$\begin{aligned}{} & {} \begin{aligned}&{\tilde{f}}_0:= \, [v_0^{\prime }(v_0^{\prime } v_0^{\prime \prime })^{\prime }]^{\prime } + \alpha _0 \textrm{d}_0 [v_0^{\prime }(v_0^{\prime } v_0^{\prime \prime })^{\prime }]^{\prime } \\&\quad + 3(\mu _d+\nu _d)v_0^{\prime \, 2} v_0^{\prime \prime } - \mu _d v_{0B}^{\prime \, 2} v_0^{\prime \prime } + \, \\&v_0^{\prime \prime } \int _{1}^{s} \int _{0}^{s^*} (\textrm{d}_0 v_0^{\prime \, 2} + v_0^{\prime } \textrm{d}_0^2 v_0^{\prime })\textrm{d}{\hat{s}}\textrm{d}{\hat{s}}^* \\&\quad + v_0^{\prime } \int _{0}^{s} (\textrm{d}_0 v_0^{\prime \, 2} + v_0^{\prime } \textrm{d}_0^2 v_0^{\prime }) \textrm{d}{\hat{s}} , \end{aligned} \end{aligned}$$
(21)
$$\begin{aligned}{} & {} {\tilde{g}}_0:= \frac{v_0^{\prime \, 2} v_0^{\prime \prime } + \alpha _0 \textrm{d}_0 (v_0^{\prime \, 2} v_0^{\prime \prime })}{2} , \end{aligned}$$
(22)
$$\begin{aligned}{} & {} {\tilde{h}}_0:= \frac{(v_0^{\prime \, 2} v_0^{\prime \prime })^{\prime } + \alpha _0 \textrm{d}_0 [(v_0^{\prime \, 2} v_0^{\prime \prime })^{\prime }]}{2} , \end{aligned}$$
(23)

with \({\tilde{g}}_{0B}\) and \({\tilde{h}}_{0B}\) denoting the values of \({\tilde{g}}_0\) and \({\tilde{h}}_0\) calculated at the abscissa of the free end B.

Let us observe that the chain of linear problems (19)–(20) have to be solved consecutively. The solution of the zero order problem (19) can be expressed in the form

$$\begin{aligned} v_0 = A(t_1,t_2,...) \phi (s) \, e^{i \omega _d t_0} + c.c. , \end{aligned}$$
(24)

where c.c. denotes complex conjugate, \(A(t_1,t_2,...)\) is an unknown (complex) amplitude, and, finally, \(\lambda =\pm i \omega _d\) and \(\phi (s)\) are the right eigenvalue and eigenfunction of the linear problem (15), at the Hopf’s bifurcation point, the latter given by Eq. (16).

By substituting Eq. (24) in the first order perturbation problem (20), this latter reads:

$$\begin{aligned} \varepsilon ^1: \,\,\, {\left\{ \begin{array}{ll} \textrm{d}_0^2 v_1 + \beta _0 \textrm{d}_0 v_1 + \alpha _0 \textrm{d}_0 v_1^{\prime \prime \prime \prime } + v_1^{\prime \prime \prime \prime }\\ \quad + 2(\mu _d+\nu _d) v_1^{\prime \prime } + \\ F_0 \, e^{i \omega _d t_0} + c.c. + n.r.t. = 0 , \\ v_{1A} = 0 , \\ v_{1A}^{\prime } = 0 , \\ v_{1B}^{\prime \prime } + \alpha _0 \textrm{d}_0 v_{1B}^{\prime \prime } + G_{0B} \, e^{i \omega _d t_0} + c.c.\\ \quad + n.r.t. = 0 , \\ -v_{1B}^{\prime \prime \prime } - \alpha _0 \textrm{d}_0 v_{1B}^{\prime \prime \prime } - 2 \nu _d v_{1B}^{\prime } - H_{0B} \, e^{i \omega _d t_0}\\ \quad + c.c. + n.r.t. = 0 , \end{array}\right. } \end{aligned}$$
(25)

where n.r.t. stands for non-resonant terms, functions \(F_0\), \(G_0\), and \(H_0\) are

$$\begin{aligned}{} & {} \begin{aligned}&F_0 = \, [(2 i \omega _d + \beta _0) \phi + \alpha _0 \phi ^{\prime \prime \prime \prime } ] \textrm{d}_1 A \\&\quad + [2(\mu _d+\nu _d) \phi ^{\prime \prime } ] A \\&\quad + [i \omega _d \beta _e \phi ^2 {\bar{\phi }} + i \omega _d \alpha _e (\phi ^{\prime \prime \, 2} {\bar{\phi }}^{\prime \prime })^{\prime \prime } + f_0] A^2 {\bar{A}} , \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned}{} & {} G_0 = [\alpha _0 \phi ^{\prime \prime }] \textrm{d}_1 A + [i \omega _d \alpha _e (\phi ^{\prime \prime \, 2} {\bar{\phi }}^{\prime \prime }) + g_0 ] A^2 {\bar{A}} ,\nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned}{} & {} H_0 = [\alpha _0 \phi ^{\prime \prime \prime }] \textrm{d}_1 A + [2 \nu _d \phi ^\prime ] A \nonumber \\{} & {} \quad + [i \omega _d \alpha _e (\phi ^{\prime \prime \, 2} {\bar{\phi }}^{\prime \prime })^{\prime } + h_0 ] A^2 {\bar{A}} , \end{aligned}$$
(28)

functions \(f_0\), \(g_0\), and \(h_0\) are given by

$$\begin{aligned}{} & {} \begin{aligned}&f_0:= \, (1+i \omega _d \alpha _0) \big (2 \phi ^{\prime \prime \prime \prime } \phi ^{\prime } {\bar{\phi }}^{\prime } + \phi ^{\prime \, 2} {\bar{\phi }}^{\prime \prime \prime \prime } + 3 \phi ^{\prime \prime \, 2} {\bar{\phi }}^{\prime \prime } \big ) \\&\quad + 4 (1+i \omega _d \alpha _0) \big ( \phi ^{\prime } \phi ^{\prime \prime } {\bar{\phi }}^{\prime \prime \prime } + \phi ^{\prime } \phi ^{\prime \prime \prime } {\bar{\phi }}^{\prime \prime } + \phi ^{\prime \prime } \phi ^{\prime \prime \prime } {\bar{\phi }}^{\prime } \big ) \\&\quad + 3(\mu _0+\nu _0) \big ( 2 \phi ^{\prime \prime } \phi ^{\prime } {\bar{\phi }}^{\prime } + \phi ^{\prime \,2} {\bar{\phi }}^{\prime \prime } \big ) \\&\quad - \mu _0 \big ( 2 \phi ^{\prime \prime } \phi _B^{\prime } {\bar{\phi }}_B^{\prime } + \phi _B^{\prime \,2} {\bar{\phi }}^{\prime \prime } \big ) + \\&\quad - 2 \omega _d^2 {\bar{\phi }}^{\prime \prime } \int _{1}^{s} \int _{0}^{s^*} \phi ^{\prime \, 2}\textrm{d}{\hat{s}}\textrm{d}{\hat{s}}^* - 2 \omega _d^2 {\bar{\phi }}^{\prime } \int _{1}^{s} \phi ^{\prime \, 2}\textrm{d}{\hat{s}} , \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}{} & {} g_0:= (1+i \omega _d \alpha _0) \big ( \phi ^{\prime \prime } \phi ^{\prime } {\bar{\phi }}^{\prime } + \frac{1}{2} \phi ^{\prime \,2} {\bar{\phi }}^{\prime \prime } \big ), \end{aligned}$$
(30)
$$\begin{aligned}{} & {} h_0:= (1+i \omega _d \alpha _0) \big ( \phi ^{\prime \prime } \phi ^{\prime } {\bar{\phi }}^{\prime } + \frac{1}{2} \phi ^{\prime \,2} {\bar{\phi }}^{\prime \prime } \big )^{\prime }, \end{aligned}$$
(31)

the overbar denotes complex conjugation and, finally, the dimensionless parameters \(\alpha _e\) and \(\beta _e\) are defined as follows:

$$\begin{aligned} \begin{array}{l} \alpha _e:= \alpha _1 + 3 \, \omega _d^2 \, \alpha _2, \, \\ \beta _e:= \beta _1 + 3 \, \omega _d^2 \, \beta _2 . \end{array} \end{aligned}$$
(32)

Parameters \(\alpha _e\) and \(\beta _e\) account for the influence of nonlinear damping on the post-critical behavior of the system. They are referred here to as equivalent nonlinear damping of the internal and external type, respectively.

Note that problem (20) is not homogenous in the unknown function \(v_1\). In order for it to be solvable, a compatibility (or solvability) condition [57] has to be satisfied. For the problem at hand, it reads:

$$\begin{aligned} G_{0B} {\bar{\psi }}_B^{\prime } - H_{0B} {\bar{\psi }}_B + \int _{0}^{1} F_0 {\bar{\psi }} \, \textrm{d}s = 0 , \end{aligned}$$
(33)

where \(\psi (s)\) is the eigenfunction of the adjoint problem of (14).

By enforcing (33), using the normalization condition \(\int _{0}^{1} \phi {\bar{\psi }} \, \textrm{d}s = 1\) for the eigenfunctions of the linear problem (14), reabsorbing the bookkeeping parameter \(\varepsilon \), and coming back to the true time, it is:

$$\begin{aligned}{} & {} c_1 {\dot{A}} + (c_{2 \mu } \delta \mu + c_{2 \nu } \delta \nu ) A + (c_{30} + c_{3 \alpha } \alpha _e \nonumber \\{} & {} \qquad + c_{3 \beta } \beta _e) A^2 {\bar{A}} = 0 , \end{aligned}$$
(34)

where the c-coefficients are defined in “Appendix C”.

Equation (34) is the complex bifurcation equation obtained by enforcing the solvability of the first order perturbation problem (25). It is a first-order ordinary differential equation (coherently with the co-dimension of the simple Hopf’s bifurcation), governs the dynamics of a reduced order model of the beam close to the Hopf’s bifurcation point, and explicitly accounts for the influence of nonlinear damping on the system dynamics via coefficient \(c_3 = c_{30} + c_{3 \alpha } \alpha _e + c_{3 \beta } \beta _e\).

Equation (34) can be recast in a real form by introducing the real amplitude a(t) and real phase \(\varphi (t)\), such that \(2 A(t)= a(t) e^{i \varphi (t)}\). By substitution, we get:

$$\begin{aligned} \begin{array}{l} {\dot{a}} + a \Big [ \rho ^a_{\mu } \delta \mu + \rho ^a_{\nu } \delta \nu + \frac{a^2}{4} (\rho ^a_0 + \rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e) \Big ] = 0 , \\ a {\dot{\varphi }} + a \Big [ \rho ^{\varphi }_{\mu } \delta \mu + \rho ^{\varphi }_{\nu } \delta \nu + \frac{a^2}{4} (\rho ^{\varphi }_0 + \rho ^{\varphi }_{\alpha } \alpha _e + \rho ^{\varphi }_{\beta } \beta _e) \Big ] = 0 , \end{array} \end{aligned}$$
(35)

where the \(\rho \)-coefficients are defined in “Appendix C”.

Steady solutions of the nonlinear ordinary differential system (35), i.e., solutions in the form \(a(t) = a_s\), \(\varphi (t) = \Psi \, t + \varphi _0\), correspond to periodic motions of the original system, with \(a_s\), \(\Psi \), \(\varphi _0\) constant parameters, representing the limit-cycle amplitude, the frequency correction, and the initial phase, respectively. Apart from the null trivial solution, steady solutions of (35) are given by:

$$\begin{aligned} \begin{array}{l} a_s^2 = \frac{-4}{\rho ^a_0 + \rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e} (\rho ^a_{\mu } \delta \mu + \rho ^a_{\nu } \delta \nu ) , \\ \Psi = \frac{\rho ^{\varphi }_0 + \rho ^{\varphi }_{\alpha } \alpha _e + \rho ^{\varphi }_{\beta } \beta _e}{\rho ^a_0 + \rho ^a_{\alpha } \alpha _e {+} \rho ^a_{\beta } \beta _e} (\rho ^a_{\mu }\delta \mu + \rho ^a_{\nu }\delta \nu ) - (\rho ^{\varphi }_{\mu }\delta \mu {+} \rho ^{\varphi }_{\nu }\delta \nu ) . \end{array} \end{aligned}$$
(36)

Characteristics of limit-cycles described by Eqs. (35)–(36) depend on the linear damping (\(\alpha _0\), \(\beta _0\)), via the \(\rho \)-coefficients, and on the nonlinear damping (\(\alpha _1\), \(\alpha _2\), \(\beta _1\), \(\beta _2\)), via the equivalent nonlinear damping parameters \(\alpha _e\) and \(\beta _e\). The influence of these latter on the dynamics of the system is discussed in Sect. 4.2, on the ground of the analytical results derived here.

4.2 Qualitative analysis

Without loss of generality, let us consider the case of a Hopf’s bifurcation point in the load parameters domain (\(\mu _d\), \(\nu _d\)) that is crossed along the direction of the \(\mu \)-axis (\(\delta \nu =0\), \(\delta \mu >0\)). The limit-cycle amplitude \(a_s\) predictable via the real form of the bifurcation Eq. (34) is given by:

$$\begin{aligned} a_s^2 = \frac{-4 \, \rho ^a_{\mu }}{\rho ^a_{0e}} \, \delta \mu , \end{aligned}$$
(37)

where \(\rho ^a_{0e} = \rho ^a_0 + \rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e\). In this case, the condition for a stable super-critical limit-cycle requires that \(\rho ^a_{\mu } / \rho ^a_{0e} <0\).

In order to discuss the beneficial or detrimental influence of the nonlinear damping on the stability of the considered system, it is observed that even assuming the equivalent nonlinear damping parameters to be positive (\(\alpha _e>0\), \(\beta _e>0\)), their influence on the stability of the system limit-cycles depends on the sign and magnitude of coefficients \(\rho ^a_{\alpha }\) and \(\rho ^a_{\beta }\). These latter, as well as coefficients \(\rho ^a_{\mu }\) and \(\rho ^a_{0}\), explicitly depend on the linear damping parameters \(\alpha _0\) and \(\beta _0\), via Eqs. (C8)–(C9). Notwithstanding this analytical dependence is not trivial, it is possible to provide a graphical representation of the \(\rho \)-coefficients as functions of \(\alpha _0\) and \(\beta _0\), see Figs. 3 and 4.

Fig. 3
figure 3

Coefficients \(\rho ^a_0\) and \(\rho ^a_{\mu }\) as functions of the linear damping parameters \(\alpha _0\) and \(\beta _0\): a \(\rho ^a_0=\rho ^a_0(\alpha _0,\beta _0)\); b \(\rho ^a_{\mu }=\rho ^a_{\mu }(\alpha _0,\beta _0\))

Full size image
Fig. 4
figure 4

Coefficients \(\rho ^a_{\alpha }\) and \(\rho ^a_{\beta }\) as functions of the linear damping parameters \(\alpha _0\) and \(\beta _0\): a \(\rho ^a_{\alpha }=\rho ^a_{\alpha }(\alpha _0,\beta _0)\); b \(\rho ^a_{\beta }=\rho ^a_{\beta }(\alpha _0,\beta _0\)); c regions of negativeness of coefficients \(\rho ^a_{\alpha }\) and \(\rho ^a_{\beta }\) in the \((\alpha _0,\beta _0)\)-plane, with indication of the three points (blue circle, red square, yellow diamond) associated with the linear damping parameters (\(\alpha _0\) and \(\beta _0\)) of the three damped systems (I, II, III) of Fig. 2-a

Full size image

Considering the linear damping domain (\(\alpha _0\), \(\beta _0\)) \(\in (0,0.1)\times (0,10)\), we observe that \(\rho ^a_{0}\) is always positive, while \(\rho ^a_{\mu }\) is always negative (Fig. 3). On the contrary, the sign of \(\rho ^a_{\alpha }\) and \(\rho ^a_{\beta }\) can change (Fig. 4), and, accordingly, it is possible to identify three kind of regions in the linear damping domain: in the first region (which contains the circle-marked point) both coefficients are negative; in the second region (which contains the square-marked point) \(\rho ^a_{\alpha }<0\) and \(\rho ^a_{\beta }>0\); finally, in the third region (which contains the diamond-marked point) both coefficients are positive. Such regions are characterized by different (detrimental or beneficial) effects of the internal and external nonlinear dampings on the system dynamics, as is summarized hereafter.

The following general conclusions can be drawn:

  • if the nonlinear damping is absent (\(\alpha _e=\beta _e=0\)), a stable super-critical limit-cycle occurs when the critical Hopf’s load is overcome (as already observed in [31]), being \(\rho ^a_{0e} \equiv \rho ^a_{0}>0\) and \(\rho ^a_{\mu }<0\) (Fig. 3);

  • if the nonlinear internal damping is present (\(\alpha _e\ne 0\)), but the nonlinear external damping is not (\(\beta _e=0\)), its effect on the system dynamics is beneficial if the point (\(\alpha _0\),\(\beta _0\)) is outside the region of negativeness of \(\rho ^a_{\alpha }\) (i.e., outside the red line in Fig. 4-c), otherwise the effect is detrimental; this result is in accordance with the findings of [31] on the influence of a Van-der-Pol-like internal damping; moreover, nonlinear external damping can mitigate the detrimental effect of internal damping forms of the Van der Pol and Rayleigh types and make the overall nonlinear damping effect beneficial;

  • if the nonlinear external damping is present (\(\beta _e\ne 0\)), but the nonlinear internal damping is not (\(\alpha _e=0\)), its effect on the system dynamics is beneficial if the point (\(\alpha _0\),\(\beta _0\)) is outside the region of negativeness of \(\rho ^a_{\beta }\) (i.e., outside the blue line in Fig. 4-c), otherwise the effect is detrimental and, moreover, adding internal damping forms of the Van der Pol and Rayleigh types would even be worsening;

  • if nonlinear dampings of the internal and external type are both present (\(\alpha _e\ne 0\), \(\beta _e\ne 0\)), their combined influence on the amplitude of the system limit-cycle can be beneficial or detrimental, depending on the balance between the overall nonlinear damping effect on one side and both the elastic and inertial nonlinear effects on the other; in particular, if \(\rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e > 0\), the nonlinear damping effect is beneficial; on the contrary, if \(\rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e < 0\), the nonlinear damping effect is detrimental; finally, the nonlinear damping may even turn a stable limit-cycle (e.g., the limit-cycle of a system with \(\rho ^a_{0}>0\), \(\rho ^a_{\mu }<0\), \(\alpha _e=\beta _e=0\)) into an unstable limit-cycle, if \(\rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e < -\rho ^a_0\).

In general, the influence of nonlinear damping forms of the internal and external types such as those considered in the present study can be either beneficial or detrimental, it depends on the value of the equivalent nonlinear dampings, \(\alpha _e\) and \(\beta _e\), and of their coefficients of influence, \(\rho ^a_{\alpha }\) and \(\rho ^a_{\beta }\). Only when all of them have the same sign the influence of nonlinear damping is expected to be beneficial, regardless of their value. In all other cases, it is necessary to check the positiveness of the linear combination \(\rho ^a_{\alpha } \alpha _e + \rho ^a_{\beta } \beta _e\). For example, assuming the nonlinear damping parameters \(\alpha _e\) and \(\beta _e\) to be positive, the effect of the nonlinear damping on the system dynamics may be detrimental within the region of the linear damping domain of Fig. 4 that contains the square-marked point (case II), it is certainly detrimental within the region of the circle-marked point (case I), and it is beneficial within the region of the diamond-marked point (case III).

5 Numerical results

In this section, results of numerical simulations are reported to corroborate the analytical findings of the present study and to emphasize crucial aspects of the nonlinear dynamics of a generalized Beck’s column in the presence of internal and external nonlinear dampings. Specifically, the results provided by the Multiple Scales Method are compared with those obtained by resorting to a purely numerical method to solve the differential problem (13). Such numerical method is based on a Galerkin discretization of the original continuous system, as is done in other works addressing the dynamics, stability, and post-critical behavior of the visco-elastic Beck’s column (see, e.g., [13, 31]). In particular, after a convergence analysis, the results of a three-modes Galerkin discretization have been selected and reported in this section. Further details about this numerical method are given in “Appendix D”.

Three paradigmatic case studies are discussed, corresponding to damped systems associated with the three marked points in Fig. 4. A summary of the main characteristics of such damped systems and case studies, in terms of linear damping parameters, Hopf’s bifurcation frequencies and critical loads, and \(\rho \)-coefficients, is reported in Table 1. It is worth to notice that, in the considered cases (I, II, III in Table 1), the linear damping produces, with respect to the undamped beam, a (medium/low) destabilizing effect (I/II) and a stabilizing effect (III), respectively.

Table 1 Linear damping parameters \(\alpha _0\) and \(\beta _0\), Hopf’s bifurcation frequency \(\omega _c\), critical value of the follower load parameter \(\mu \) (under null dead load, \(\nu =0\)), and corresponding values of \(\rho \)-coefficients (\(\rho ^a_0\), \(\rho ^a_{\alpha }\), \(\rho ^a_{\beta })\) for the three case studies (I, II, III)
Full size table

For the above case studies, Fig. 5 provides a graphical representation, namely, a bifurcation chart, of the type of limit-cycles (super- or sub-critical) to which the damped systems may tend, as a function of the nonlinear damping parameters (\(\alpha _e\), \(\beta _e\)). The blue lines in the three cases in Fig. 5 correspond to the combinations of \(\alpha _e\) and \(\beta _e\) that make \(\rho _{0e}=0\). Such lines separate the domain of the nonlinear damping parameters in two regions: in the white region \(\rho _{0e}>0\) (this is associated with super-critical limit-cycles); in the grey region \(\rho _{0e}<0\) (condition for sub-critical limit-cycles).

Fig. 5
figure 5

Bifurcation chart of the post-critical behavior of the system in the (\(\alpha _e\), \(\beta _e\))-plane, for the three case studies, respectively: a case study I; b case study II; c case study III. Blue lines correspond to the combinations of \(\alpha _e\) and \(\beta _e\) for which \(\rho _{0e}=0\); SUP stands for super-critical, SUB stands for sub-critical

Full size image

It is worth noting that in the case study I, the blue line in Fig. 5 has negative slope and represents an upper limit to the values of \(\alpha _e\) and \(\beta _e\) that allow the expected limit-cycle of the system to remain super-critical and stable. In other words, positive values of \(\alpha _e\) and \(\beta _e\) cannot be too large, otherwise the system stability may be compromised. This seems to represent a paradoxical effect of the nonlinear damping, but it is not so much surprising as even the linear internal damping may have a detrimental influence on the system dynamics, as is well-known [30]. In the second case study, the blue line in Fig. 5 represents a similar constraint on the values of \(\alpha _e\) and \(\beta _e\) that allow the system limit-cycle to remain super-critical and stable, but its slope is positive. Finally, the blue line associated with the third case study in Fig. 5 has negative slope and lies outside the region of positive values of \(\alpha _e\) and \(\beta _e\): this means, for instance, that in such case any combination of positive nonlinear damping parameters (\(\alpha _1\),\(\alpha _2\),\(\beta _1\),\(\beta _2\)) produces positive values of the equivalent nonlinear damping parameters (\(\alpha _e\), \(\beta _e\)) and is expected to be beneficial and to reduce the amplitude of the super-critical, stable limit-cycle of the system.

Bifurcation charts such as those in Fig. 5 provide indications on the combinations of nonlinear damping parameters that may compromise the system stability. To better clarify this point and provide further explanations, let us study more in detail the three cases denoted with the letters A, B, and C in Fig. 5-b. They correspond to three damped systems, referred to here as II\(_A\), II\(_B\), and II\(_C\), having the same linear damping (\(\alpha _0=0.010\), \(\beta _0=1\)), but different nonlinear damping (\(\alpha _e\), \(\beta _e\)). In particular, moving from A to C in Fig. 5-b, the detrimental effect of nonlinear damping increases.

Figure 6 reports bifurcation diagrams of the damped systems II\(_A\), II\(_B\), and II\(_C\) in the domain \(a_s\)-\(\delta \mu \), where \(a_s\) is the asymptotic amplitude of the system limit-cycle (as per formula (37)) and \(\delta \mu \) is the load parameter increment measured from the bifurcation point. The blue lines (MSM) in Fig. 6 correspond to the bifurcation diagrams obtained via the Method of Multiple time Scale, while the red marks (GAL) are associated with the corresponding diagrams derived via a numerical procedure based on a Galerkin discretization of the original system to solve problem (13).

Fig. 6
figure 6

Bifurcation diagrams reporting the asymptotic amplitude \(a_s\) (as per formula (37)) versus the load parameter increment \(\delta \mu \), for three paradigmatic systems having the same linear dampings (\(\alpha _0=0.010\), \(\beta _0=1\)) and different nonlinear dampings (\(\alpha _e\), \(\beta _e\)): a system without nonlinear damping \(\alpha _e=0\), \(\beta _e=0\) (super-critical); b system with nonlinear damping \(\alpha _e=0.005\), \(\beta _e=0.005\) (super-critical); c system with nonlinear damping \(\alpha _e=0.025\), \(\beta _e=0.005\) (sub-critical)

Full size image

As is apparent from Fig. 6, the three damped systems, II\(_A\), II\(_B\), II\(_C\), have the following characteristics: the first is (a) a system without nonlinear damping (\(\alpha _e=\beta _e=0\)), whose limit-cycles predicted by both methods (MSM and GAL) are super-critical and stable; the second is (b) a system with nonlinear damping parameters \(\alpha _e=\beta _e=0.005\), whose limit-cycles are still super-critical and stable, notwithstanding the detrimental influence of the considered nonlinear damping; finally, the third is (c) a system with nonlinear damping parameters \(\alpha _e=0.025\) and \(\beta _e=0.005\), whose limit-cycles predicted via the Multiple Scales Method (MSM) would be of the sub-critical unstable type, but the Galerkin-based numerical approach shows the situation is bit more involved than the prediction at the first-order of the Method of Multiple Scales for this system. In particular, the presence of a turning point in the bifurcation diagram of Fig. 6-c is observed, which is not a simple parabola, but at least a higher order polynomial curve. The turning point splits such curve in two parts: the upper part (above the turning point) is associated with stable limit-cycles, while the lower part correspond to limit-cycles that cannot be actually reached by the system. In other words, negative increments of the load parameter \(\delta \mu \) make the asymptotic system motion to vanish (\(a_s=0\)) or make it tend towards values of \(a_s\) belonging to the upper part of the bifurcation curve, depending on the initial conditions of the system.

This kind of behavior is the so-called Hard Loss of Stability Phenomenon, already observed for the Ziegler’s double pendulum in [27] and for the Beck’s column in the presence of a Van-der-Pol-like internal damping in [31]. This phenomenon entails, via a turning point, a regain of stability of the sub-critical branches predicted by the first-order analysis. Therefore, when the load parameter \(\mu \) is increased from the critical value \(\mu _d\), the limit-cycle amplitude suddenly “jumps” to a finite value, that could be unacceptable and dangerous from an engineering point of view. However, to predict analytically phenomena of this kind it is necessary to push the Multiple Scales algorithm one step further, that is, to the second order problem, as done in [27] for the Ziegler’s double pendulum, but this out of the scope of the present work and will be addressed in a subsequent investigation.

This section is concluded by comparing the time histories of the transverse displacement of the beam tip v(1, t) obtained by numerical integration of the bifurcation Eq. (35) and the corresponding time histories derived by resorting to the Galerkin’s approach to solve problem (13). Specifically, Fig. 7 illustrates the time histories of the tip displacement v(1, t) for the three damped systems associated with the case studies I, II, and III in absence of nonlinear damping (\(\alpha _e=0\), \(\beta _e\)=0), when the increment of the load parameter is \(\delta \mu = 0.01 \mu _d\) (\(\delta \nu =0\)). Figure 8 reports the corresponding time histories when the nonlinear damping is present and is associated with nonlinear damping parameters \(\alpha _e=0.005\) and \(\beta _e\)=0.005.

Fig. 7
figure 7

Time histories of the tip displacement v(1, t), via the method of multiple time scales (MSM, blue) and the numerical method based on Galerkin’s appoarch (GAL, grey), for three case studies (I, II, III), when \(\delta \mu = 0.01 \mu _d\) and \(\delta \nu =0\), in absence of nonlinear damping (\(\alpha _e=0\), \(\beta _e\)=0); \(a_s\) is the asymptotic amplitude as per formula (37)

Full size image
Fig. 8
figure 8

Time histories of the tip displacement v(1, t), via the method of multiple time scales (MSM, blue) and the numerical method based on Galerkin’s appoarch (GAL, grey), for three case studies (I, II, III), when \(\delta \mu = 0.01 \mu _d\) and \(\delta \nu =0\), in presence of nonlinear damping (\(\alpha _e=0.005\), \(\beta _e\)=0.005); \(a_s\) is the asymptotic amplitude as per formula (37)

Full size image

Figures 7 and 8 show a very good agreement between the numerical solution of problem (13) based on a three-modes Galerkin’s method (reported in grey) and the amplitude of the relevant limit-cycle obtained as solution of the bifurcation Eq. (35) (represented in blue), whose stationary asymptotic value coincides with the prediction of the simple formula (37).

Looking at the results obtained, it is apparent that the numerical results reported and discussed in this section are in good agreement with the predictions based on the analytical findings of the previous section. However, apart from the quantitative accordance between the results of the two approaches observed in the foregoing, from a qualitative standpoint we remark a clear increase of the limit-cycle amplitudes in the cases studies I and II when the internal and external nonlinear dampings are introduced in the system (detrimental effect of nonlinear damping), and a reduction (beneficial effect) in the third case study, as it is expected.

6 Conclusions

The influence of nonlinear damping of the internal and external type on the dynamics of a generalized Beck’s column has been addressed in the paper. A variational principle has been exploited to get the equations of motion and the natural boundary conditions that govern the dynamic behavior of the system. A first-order perturbation analysis, based on the Method of Multiple Scales, has been directly performed on the continuous system, to derive the system bifurcation equations. This asymptotic, analytical approximation of the system behavior close to a Hopf’s bifurcation point has allowed to study analytically the corresponding limit-cycles of the system and to shed the light on the combined effect of the internal and external nonlinear dampings on the stability and post-critical behavior of the system. The main findings can be summarized in what follows.

  • In the absence of nonlinear damping a stable, super-critical limit-cycle manifests itself, thus confirming the results of [31].

  • Both nonlinear internal and external damping forms have a double nature, namely: each of them can be beneficial or detrimental, in terms of reducing or increasing the limit-cycle amplitude.

  • When only nonlinear internal damping of Van der Pol type is present, as in [31], its effect on the limit-cycle amplitude can be beneficial or detrimental, depending on the sign of the related coefficient of influence (which, in turn, is a function of the linear damping parameters) in the bifurcation equation; in this framework, adding internal damping of Rayleigh type does not qualitatively change this behavior, but an external nonlinear damping can mitigate the detrimental effect of the nonlinear internal damping and make the overall nonlinear damping effect beneficial, as it is shown in the paper.

  • When only nonlinear external damping of Van der Pol (or Rayleigh) type is present, it can reduce (beneficial effect) or increase (detrimental effect) the limit-cycle amplitude, thus having, from a qualitative point of view, the same effect of the nonlinear internal damping; moreover, when the effect of the considered nonlinear external damping is detrimental, adding internal damping forms of the Van der Pol and Rayleigh types would not be helpful.

  • Super-critical (stable) as well as sub-critical (unstable) limit-cycles can manifest themselves depending on the balance between the overall (internal and/or external) nonlinear damping effect on one side, and both the elastic and inertial nonlinear contributions on the other, thus extending the results of [31] also in the presence of internal nonlinear damping of Rayleigh type and of external nonlinear dampings of Rayleigh and Van der Pol types.

  • The presence of the so-called Hard Loss of Stability phenomenon, already observed for the Ziegler’s double pendulum in [27] and for the Beck’s column in the presence of a Van-der-Pol-like internal damping in [31] is confirmed in this work. This phenomenon entails that a periodic sub-critical branch turns back, regaining stability and, consequently, as soon as the critical load is overcome, a large amplitude limit-cycle manifests itself, not going to zero at the critical load.

  • The interaction between nonlinear internal and external damping forms has been detected, primarily by showing that the linear damping parameter plane can be divided into different regions in which just one (or both) of the nonlinear damping forms could entail a beneficial effect on the system limit-cycle amplitude. Moreover, bifurcation charts have been built-up, revealing the existence of two regions in the plane of the nonlinear damping coefficients, in which super- or sub-critical limit-cycles take place. In the sub-critical regions, due to the Hard Loss of stability phenomenon, a regain of stability has been numerically detected.

The analytical results derived in the paper have been validated by comparisons with benchmark solutions obtained by resorting to a numerical method based on a Galerkin discretization of the original system. To this end, three damped beams, for which linear damping produces (I) a medium destabilizing effect, (II) a low destabilizing effect, and (III) a stabilizing effect, respectively, have been considered. The numerical analysis has confirmed that both the internal and external nonlinear damping forms can be beneficial or detrimental, as we can predict a-priori on the ground of the analytical results derived and discussed in the paper.

Several aspects deserve further investigation and will be addressed in future woks, e.g.: i) the analytical study of the dynamic behavior of the system close to double-zero bifurcation points, as is done in [30] for a nonlinear visco-elastic beam in presence of linear damping; ii) the extension of the analysis of the present study to the second order problem of the Method of Multiple Scales, to be also able to detect analytically the Hard Loss of Stability phenomenon and the related turning points in the bifurcation diagrams (as is done in [27] for the Ziegler’s double pendulum); iii) the analytical investigation of the influence of non-uniform cross-sectional properties (associated with variations in the cross-section geometry and material properties, as in [58, 59]) on the nonlinear dynamics of the generalized visco-elastic Beck’s column.