Skip to main content
SpringerLink
Log in

Nonlinear free vibrations of Timoshenko–Ehrenfest beams using finite element analysis and direct scheme

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

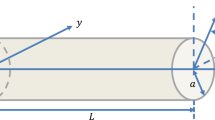
In this work, nonlinear free vibrations of fully geometrically exact Timoshenko–Ehrenfest beams are investigated. First, the exact strong form of the Timonshenko–Ehrenfest beam, considering the geometrical nonlinearity, is derived, and the required formulations are obtained. Since the strong forms of governing equations are highly nonlinear, a nonlinear finite element analysis (FEA) is employed to obtain the weak form. The FEA is utilized to compute natural frequencies and mode shapes; the direct scheme is adopted to solve the eigenvalue problem which is obtained by eliminating nonlinear terms. Then, each eigenvector is normalized, and the nonlinear stiffness matrix is derived and the nonlinear free vibration analysis is carried out. A recursive procedure is adopted to proceed until the convergence criterion is satisfied. Finally, the applicability of the proposed formulation is provided with some examples and results are compared with those available in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability statement

Data can be made available upon reasonable request.

References

  1. Amabili, M., Ferrari, G., Ghayesh, M.H., Hameury, C., Zamal, H.H.: Nonlinear vibrations and viscoelasticity of a self-healing composite cantilever beam: theory and experiments. Compos. Struct. 294, 115741 (2022)

    Article  Google Scholar 

  2. Alambeigi, K., Mohammadimehr, M., Bamdad, M., Rabczuk, T.: Free and forced vibration analysis of a sandwich beam considering porous core and SMA hybrid composite face layers on Vlasov’s foundation. Acta Mech. 231, 3199–3218 (2020)

    Article  MathSciNet  Google Scholar 

  3. Aria, A.I., Friswell, M.I., Rabczuk, T.: Thermal vibration analysis of cracked nanobeams embedded in an elastic matrix using finite element analysis. Compos. Struct. 212, 118–128 (2019)

    Article  Google Scholar 

  4. Balasubramanian, P., Franchini, G., Ferrari, G., Painter, B., Karazis, K., Amabili, M.: Nonlinear vibrations of beams with bilinear hysteresis at supports: Interpretation of experimental results. J. Sound Vib. 499, 115998 (2021)

    Article  Google Scholar 

  5. Bhashyam, G.R., Prathap, G.: Galerkin finite element method for non-linear beam vibrations. J. Sound Vib. 72, 191–203 (1980)

    Article  Google Scholar 

  6. Dadgar-Rad, F., Firouzi, N.: Large deformation analysis of two-dimensional visco-hyperelastic beams and frames. Arch. Appl. Mech. 91, 4279–4301 (2021)

    Article  Google Scholar 

  7. Ding, H., Chen, L.-Q.: Natural frequencies of nonlinear vibration of axially moving beams. Nonlinear Dyn. 63, 125–134 (2011)

    Article  MathSciNet  Google Scholar 

  8. Ding, H., Li, Y., Chen, L-Q.: Nonlinear vibration of a beam with asymmetric elastic supports. Nonlinear Dyn. (2018)

  9. Firouzi, N., Kazemi, S.R.: Investigation on dynamic stability of Timoshenko beam using parametric excitation. Appl. Phys. A 129, 869 (2023)

    Article  Google Scholar 

  10. Ghayesh, M.H., Amabili, M.: Nonlinear vibration and stability of an axially moving Timoshenko beam with an intermediate spring support. Mech. Mach. Theory 67, 1–16 (2013)

    Article  Google Scholar 

  11. Ghayesh, M.H., Amabili, M.: Three-dimensional nonlinear planar dynamics of an axially moving Timoshenko beam. Arch. Appl. Mech. 83, 591–604 (2013)

    Article  Google Scholar 

  12. Ghayesh, M.H., Amabili, M.: Nonlinear dynamics of an axially moving Timoshenko beam with an internal resonance. Nonlinear Dyn. 73, 39–52 (2013)

    Article  MathSciNet  Google Scholar 

  13. Karami, B., Janghorban, M., Rabczuk, T.: Dynamics of two-dimensional functionally graded tapered Timoshenko nanobeam in thermal environment using nonlocal strain gradient theory. Compos. B Eng. 182, 107622 (2020)

    Article  Google Scholar 

  14. Khaniki, H.B., Ghayesh, M.H., Chin, R., Amabili, M.: Large amplitude vibrations of imperfect porous-hyperelastic beams via a modified strain energy. J. Sound Vib. 513, 116416 (2021)

    Article  Google Scholar 

  15. Lee, S.Y., Ke, H.Y., Kou, Y.H.: Analysis of non-uniform beam vibration. J. Sound Vib. 142, 15–29 (1990)

    Article  Google Scholar 

  16. Lenci, S., Rega, G.: Nonlinear free vibration of planar elastic beam: a unified treatment of geometrical and mechanical effects. Procedia IUTAM 19, 35–42 (2016)

    Article  Google Scholar 

  17. Lenci, S., Rega, G.: Axial-transversal coupling in the free nonlinear vibrations of Timoshenko beams with arbitrary slenderness and axial boundary conditions. Proc. R. Soc. A 472, 20160057 (2016)

    Article  MathSciNet  Google Scholar 

  18. Lenci, S., Clementi, F., Rega, G.: A comprehensive analysis of hardening/softening behaviour of shearable planar beams with whatever axial boundary constraint. Meccanica 51, 2589–2606 (2016)

    Article  MathSciNet  Google Scholar 

  19. Lenci, S., Clementi, F.: Axial-transversal coupling in the nonlinear dynamics of a beam with an inclined roller. Int. J. Mech. Sci. 144, 490–501 (2018)

    Article  Google Scholar 

  20. Manolis, G.D., Beskos, D.E.: Thermally induced vibrations of beam structures. Comput. Methods Appl. Mech. Eng. 21, 337–355 (1980)

    Article  MathSciNet  Google Scholar 

  21. Mei, C.: Finite element displacement method for large amplitude free flexural vibrations of beams and plates. Comput. Struct. 3, 163–174 (1973)

    Article  Google Scholar 

  22. Rakowski, J., Guminiak, M.: Non-linear vibration of Timoshenko beams by finite element method. J. Theor. Appl. Mech. 53, 731–743 (2015)

    Article  Google Scholar 

  23. Ribeiro, P., Petyt, M.: Non-linear vibration of beams with internal resonance by the hierarchical finite-element method. J. Sound Vib. 244, 591–624 (1999)

    Article  Google Scholar 

  24. Sato, H.: Free vibration of beams with abrupt changes of cross-section. J. Sound Vib. 89, 59–64 (1983)

    Article  Google Scholar 

  25. Sarma, B.S., Varadan, T.K.: Ritz finite element approach to nonlinear vibrations of beams. Int. J. Numer. Meth. in Eng. 20, 353–367 (1984)

    Article  Google Scholar 

  26. Sarma, B.S., Varadan, T.K.: Ritz finite element approach to nonlinear vibrations of Timoshenko beam. Commun Appl Numer Methods. 1, 23–32 (1985)

    Article  Google Scholar 

  27. Singh, S., Sharma, A.K., Rao, G.V.: Large-amplitude free vibrations of beams—a discussion on various formulations and assumptions. J. Sound Vib. 142, 77–85 (1990)

    Article  Google Scholar 

  28. Srinivasan, A.V.: Non-linear vibrations of beams and plates. Int. J. Non-linear Mech. 1, 179–191 (1966)

    Article  Google Scholar 

  29. Shen, M.-H.H., Chu, Y.C.: Vibrations of beams with a fatigue crack. Comput. Struct. 45, 79–93 (1992)

    Article  Google Scholar 

  30. Utzeri, M., Sasso, M., Chiappini, G., Lenci, S.: Nonlinear vibration of a composite beam in large displacements: analytical, numerical, and experimental approaches. J. Comput. Nonlinear Dyn. 16, 2 (2021)

    Google Scholar 

  31. Wickert, J.A.: Non-linear vibration of a traveling tensioned beam. Int. J. Non-linear Mech. 27, 503–517 (1992)

    Article  Google Scholar 

  32. Woinowsky-Krieger, S.: The effect of an axial force on the vibration of hinged bars. Trans. Am. Soc. Mech. Eng. 72, 35–36 (1950)

    MathSciNet  Google Scholar 

  33. Zhong, H., Guo, Q.: Nonlinear vibration analysis of Timoshenko beams using the differential quadrature method. Nonlinear Dyn. 32, 223–234 (2003)

    Article  Google Scholar 

  34. Żur, K.K., Firouzi, N., Rabczuk, T., Zhuang, X.: Large deformation of hyperelastic modified Timoshenko–Ehrenfest beams under different types of loads. Comput. Methods Appl. Mech. Eng.Eng. 416, 116368 (2023)

    Article  MathSciNet  Google Scholar 

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Institute of Structural Mechanics, Bauhaus-University Weimar, Weimar, Germany

    Nasser Firouzi & Timon Rabczuk

  2. Department of Civil and Building Engineering, and Architecture (DICEA), Polytechnic University of Marche, Via Brecce Bianche, 60131, Ancona, Italy

    Stefano Lenci

  3. School of Engineering, Westlake University, Hangzhou, People’s Republic of China

    Marco Amabili

  4. Department of Mechanical Engineering, McGill University, Montreal, PQ, H3A 2K6, Canada

    Marco Amabili

Authors
  1. Nasser Firouzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stefano Lenci
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marco Amabili
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Timon Rabczuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualization was done by NF and SL, formulation derivation and analyses were performed by NF. Data preparation was done by SL, MA, and TR. The first draft of the manuscript was written by NF. Supervision and editing the manuscript were done by MA, TR, and SL. All authors commented and reviewed the manuscript and approved the final version of it.

Corresponding author

Correspondence to Nasser Firouzi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

It is known that in FE derivation, it is convenient to work in natural coordinates. The relation between two different coordinates is as follows:

$$ {\text{d}}x = \frac{{{\text{d}}x}}{{{\text{d}}\xi }}{\text{d}}\xi = J{\text{d}}\xi ,\,\,\,\,\,\,\,\,\,\,\frac{{{\text{d}}\left( * \right)}}{{{\text{d}}x}} = \frac{{{\text{d}}\left( * \right)}}{{{\text{d}}\xi }}\frac{{{\text{d}}\xi }}{{{\text{d}}x}} = J^{ - 1} \frac{{{\text{d}}\left( * \right)}}{{{\text{d}}\xi }} $$
(36)

The arrays of the stiffness and mass matrices are derived as follows:

$$ \left( {K_{uu} } \right)_{11} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(37)
$$ \left( {K_{uu} } \right)_{12} = \left( {K_{uu} } \right)_{21} = - \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(38)
$$ \left( {K_{uu} } \right)_{22} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{1}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{1}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(39)
$$ \left( {K_{uw} } \right)_{11} = - \frac{{K_{S} \left( {\theta_{1}^{e} + \theta_{2}^{e} + 2\arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{h_{e} - u_{1}^{e} + u_{2}^{e} }}} \right)} \right)}}{{2\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(40)
$$ \left( {K_{uw} } \right)_{12} = \left( {K_{uw} } \right)_{21} = \frac{{K_{S} \left( {\theta_{1}^{e} + \theta_{2}^{e} + 2\arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{h_{e} - u_{1}^{e} + u_{2}^{e} }}} \right)} \right)}}{{2\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(41)
$$ \left( {K_{uw} } \right)_{22} = - \frac{{K_{S} \left( {\theta_{1}^{e} + \theta_{2}^{e} + 2\arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{h_{e} - u_{1}^{e} + u_{2}^{e} }}} \right)} \right)}}{{2\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(42)
$$ \left( {K_{u} } \right)_{11} = - \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{{}} }} - \frac{1}{2} $$
(43)
$$ \left( {K_{u} } \right)_{12} = - \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{{}} }} - \frac{1}{2} $$
(44)
$$ \left( {K_{u} } \right)_{21} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{{}} }} - \frac{1}{2} $$
(45)
$$ \left( {K_{u} } \right)_{22} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{{}} }} - \frac{1}{2} $$
(46)
$$ \left( {K_{ww} } \right)_{11} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(47)
$$ \left( {K_{ww} } \right)_{12} = \left( {K_{ww} } \right)_{21} = - \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(48)
$$ \left( {K_{ww} } \right)_{22} = \frac{{K_{0} }}{{h_{e}^{{}} \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{{2h_{e}^{2} }} - \frac{1}{{2h_{e}^{{}} }} $$
(49)
$$ \left( {K_{w\theta } } \right)_{11} = \frac{{K_{S} h_{e} \left( {u_{1}^{e} - u_{2}^{e} - h_{e} } \right)}}{{2\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{2} $$
(50)
$$ \left( {K_{w\theta } } \right)_{12} = \frac{{K_{S} h_{e} \left( {u_{1}^{e} - u_{2}^{e} - h_{e} } \right)}}{{2\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{2} $$
(51)
$$ \left( {K_{w\theta } } \right)_{21} = - \frac{{K_{S} h_{e} \left( {u_{1}^{e} - u_{2}^{e} - h_{e} } \right)}}{{2\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{2} $$
(52)
$$ \left( {K_{w\theta } } \right)_{22} = - \frac{{K_{S} h_{e} \left( {u_{1}^{e} - u_{2}^{e} - h_{e} } \right)}}{{2\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }} - \left( {u_{1}^{e} - u_{2}^{e} } \right) + \frac{{\sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } }}{2} $$
(53)
$$ \left( {K_{w} } \right)_{11} = - \frac{{K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{\left( {h_{e} - u_{1}^{e} + u_{2}^{e} } \right)^{2} }}} \right)}}{{\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(54)
$$ \left( {K_{w} } \right)_{12} = - \frac{{K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{\left( {h_{e} - u_{1}^{e} + u_{2}^{e} } \right)^{2} }}} \right)}}{{\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(55)
$$ \left( {K_{w} } \right)_{21} = \frac{{K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{\left( {h_{e} - u_{1}^{e} + u_{2}^{e} } \right)^{2} }}} \right)}}{{\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(56)
$$ \left( {K_{w} } \right)_{22} = \frac{{K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{\left( {h_{e} - u_{1}^{e} + u_{2}^{e} } \right)^{2} }}} \right)}}{{\sqrt {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} } }} $$
(57)
$$ \left( {K_{\theta \theta } } \right)_{11} = - \frac{{K_{S} \left( {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \,\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \,\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + 3\frac{{K_{2} }}{{K_{S} }}} \right)}}{{3\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right)}} $$
(58)
$$ \left( {K_{\theta \theta } } \right)_{12} = \left( {K_{\theta \theta } } \right)_{21} = \frac{{ - K_{S} \left( {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \,\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \,\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} - 6\frac{{K_{2} }}{{K_{S} }}} \right)}}{{6\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right)}} $$
(59)
$$ \left( {K_{\theta \theta } } \right)_{22} = - \frac{{K_{S} \left( {h_{e}^{2} - 2h_{e} \left( {u_{1}^{e} - u_{2}^{e} } \right) + \,\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} + \,\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + 3\frac{{K_{2} }}{{K_{S} }}} \right)}}{{3\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right)}} $$
(60)
$$ \left( {K_{\theta } } \right)_{11} = \frac{1}{2}K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{u_{1}^{e} - u_{2}^{e} - h_{e} }}} \right)\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e}^{{}} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right) $$
(61)
$$ \left( {K_{\theta } } \right)_{12} = \left( {K_{\theta } } \right)_{21} = \frac{1}{2}K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{u_{1}^{e} - u_{2}^{e} - h_{e} }}} \right)\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e}^{{}} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right) $$
(62)
$$ \left( {K_{\theta } } \right)_{12} = \frac{1}{2}K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{u_{1}^{e} - u_{2}^{e} - h_{e} }}} \right)\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e}^{{}} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right) $$
(63)
$$ \left( {K_{\theta } } \right)_{22} = \frac{1}{2}K_{S} \arctan \left( {\frac{{w_{1}^{e} - w_{2}^{e} }}{{u_{1}^{e} - u_{2}^{e} - h_{e} }}} \right)\left( {\frac{{\left( {u_{1}^{e} - u_{2}^{e} } \right)^{2} }}{{h_{e}^{{}} }} - 2\left( {u_{1}^{e} - u_{2}^{e} } \right) + \sqrt {\left( {w_{1}^{e} - w_{2}^{e} } \right)^{2} + h_{e}^{2} } } \right) $$
(64)
$$ \begin{gathered} \left( {K_{W\theta } } \right)_{11} = \left( {K_{W\theta } } \right)_{12} = \left( {K_{W\theta } } \right)_{21} = \left( {K_{W\theta } } \right)_{22} = 0 \hfill \\ \left( {K_{UW} } \right)_{11} = \left( {K_{UW} } \right)_{12} = \left( {K_{UW} } \right)_{21} = \left( {K_{UW} } \right)_{22} = 0 \hfill \\ \left( {K_{\theta W} } \right)_{11} = \left( {K_{\theta W} } \right)_{12} = \left( {K_{\theta W} } \right)_{21} = \left( {K_{\theta W} } \right)_{22} = 0 \hfill \\ \left( {K_{\theta U} } \right)_{11} = \left( {K_{\theta U} } \right)_{12} = \left( {K_{\theta U} } \right)_{21} = \left( {K_{\theta U} } \right)_{22} = 0 \hfill \\ \end{gathered} $$
(65)
$$ \left( {M_{uu} } \right)_{11} = \left( {M_{uu} } \right)_{22} = \frac{{h_{e} m_{0} }}{3},\,\,\,\left( {M_{uu} } \right)_{12} = \left( {M_{uu} } \right)_{21} = \frac{{h_{e} m_{0} }}{6} $$
(66)
$$ \left( {M_{ww} } \right)_{11} = \left( {M_{ww} } \right)_{22} = \frac{{h_{e} m_{0} }}{3},\,\,\,\left( {M_{ww} } \right)_{12} = \left( {M_{ww} } \right)_{21} = \frac{{h_{e} m_{0} }}{6} $$
(67)
$$ \left( {M_{\theta \theta } } \right)_{11} = \left( {M_{\theta \theta } } \right)_{22} = \frac{{h_{e} m_{2} }}{3},\,\,\,\,\left( {M_{\theta \theta } } \right)_{12} = \left( {M_{\theta \theta } } \right)_{21} = \frac{{h_{e} m_{2} }}{6} $$
(68)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Firouzi, N., Lenci, S., Amabili, M. et al. Nonlinear free vibrations of Timoshenko–Ehrenfest beams using finite element analysis and direct scheme. Nonlinear Dyn 112, 7199–7213 (2024). https://doi.org/10.1007/s11071-024-09403-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-024-09403-3

Keywords

Search

Navigation