1 Introduction

The analytical modeling and prediction of the response of hysteretic systems is an area of growing interest in physics, engineering, and material science since hysteresis is an almost ubiquitous nonlinear phenomenon.

For instance, electrical systems often exhibit nonlinear hysteretic behavior, a peculiar feature common to magnetic ones as well [1]. Analogously, the cardiovascular system, along with other biological systems, also exhibits a nonlinear response, having a hysteretic nature, to changes in blood pressure [2]. Mechanical systems such as engines and machines may exhibit nonlinear hysteretic behavior as a result of the nonlinear behavior of the materials used in their construction [3,4,5]. Finally, civil engineering structures exhibit nonlinear hysteretic behavior when exposed to large-amplitude vibrations due, e.g., to wind loads or earthquakes. Moreover, hysteresis is often deliberately incorporated into the system to influence its behavior in a controlled manner [6,7,8].

The occurrence of hysteresis in such a wide range of materials and systems used in different fields underscores the importance of understanding the influence of hysteresis in the design and analysis of structures subjected to cyclic loading. An accurate modeling of hysteresis is crucial for researchers and designers to better grasp and predict the behavior of systems under different conditions, which can significantly impact the design and optimization of different devices and processes.

Over the years, many mathematical models have been developed to accurately reproduce experimentally measured hysteretic behaviors. Focusing on mechanical hysteresis only, some of the well-known phenomenological models include the models by Bouc and Wen [9, 10], by Baber and Noori [11, 12], by Preisach [13], by Vaiana et al [14, 15] and by Graesser and Cozzarelli [16]. However, one of the main limitations of these models is their inability to capture different types of hysteretic behavior in a unified manner. In fact, each model is most effective at modeling systems with specific hysteretic behavior and may not be accurate for other complex loop shapes. Additionally, the parameters of such models do not always have a clear mechanical interpretation, making it challenging to determine their values only on the basis of physical experiments. Consequently, it is often necessary to use a combination of experimental testing and numerical optimization techniques to accurately estimate the parameters of the adopted model. This makes it difficult to apply these models to real-world systems without significant computational resources and experimental data.

To overcome these difficulties, Vaiana and Rosati [17] introduced a new approach for modeling rate-independent hysteretic behavior in mechanical systems and materials. Upon classifying complex hysteresis loops, ranging from asymmetric to flag-shaped, they proposed a novel rate-independent hysteretic model, denominated VRM, having an exponential nature and allowing for closed-form expressions in the evaluation of the output variable. In particular, the VRM enables uncoupled modeling of the loading and unloading phases and allows for a straightforward identification procedure due to the clear interpretation of the involved parameters. More recently, Vaiana and Rosati [18] improved their original model by formulating the VRM+A and proposed in addition a differential formulation, namely VRM+D, in order to allow for its use in the field of nonlinear dynamics. To sum up, both the original and the improved models formulated by Vaiana and Rosati address the difficulties associated with modeling hysteretic behavior quite efficiently and offer a practical solution for analyzing hysteretic mechanical systems subjected to time-periodic inputs.

Hence, it is natural to evaluate the adequacy of the VRM+D in addressing the search for periodic solutions of hysteretic mechanical systems and evaluating their stability and bifurcation. In the literature, both analytical and numerical techniques have been used to study this phenomenon; to the first class belongs the method of slowly varying parameters [19] and the harmonic balance method [20, 21]. They have been used to obtain the steady-state dynamics of Single-Degree-of-Freedom (SDoF) hysteretic mechanical systems subjected to time-periodic forcing input. Interestingly, it has been found that the response of these systems can be multivalued and include jumps, which contradicts a widely-held belief in the early sixties according to which all hysteretic systems should have stable and single-valued frequency-response curves [22, 23].

On the other hand, when dealing with strong nonlinearities, such as those found in hysteretic mechanical systems, and in situations where global dynamic behaviors are involved, numerical techniques are often necessary. Some of these techniques include frequency-domain, time-domain, and frequency/time-domain methods. A well-established and powerful numerical strategy to find periodic solutions and determine their stability and bifurcations is the Poincaré map-based method developed in [24], often used in conjunction with Floquet theory. Specifically, this method was applied to investigate the response and stability of elastoplastic oscillators. Additionally, in a later work by Lacarbonara and Vestroni [25], the responses and stability of SDoF hysteretic mechanical systems endowed with Bouc–Wen and Masing hysteretic models were examined using the Poincaré map-based method in the time domain.

In this paper, we show how the unifying modeling features of the VRM+D [18] are carried over to an accurate prediction of periodic solutions for mechanical systems characterized by hysteretic response of complex shape. The result is obtained by combining the VRM+D with Lacarbonara’s continuation method [24] and systematically constructing a series of frequency-response curves. By means of such curves, the steady-state response, stability, and bifurcation of the systems are illustrated and discussed for each shape of the assumed hysteretic behavior.

The paper is structured as follows: In Sect. 2, we describe the Poincaré map-based continuation method used to solve the fixed-point equation by the pseudo-arclength continuation method in order to find periodic solutions, determine stability and bifurcation in the state-space. In Sect. 3, we present the equations of motion in both the dimensional and non-dimensional systems, by developing the non-dimensional VRM+D. Finally, Sect. 4 outlines the numerical tests performed to analyze the frequency-response curves, stability, and bifurcations of four hysteretic mechanical systems with complex hysteresis loop shapes simulated using the non-dimensional VRM+D, as well as the methods employed for these tests.

2 Brief review of the Poincaré map-based continuation method

This section presents a brief overview of the Poincaré map-based continuation procedure, in the form originally introduced in [24], to facilitate the efficient numerical calculation of periodic solutions for hysteretic dynamical systems subjected to a time-periodic input. This method also enables the determination of stability and bifurcations through the use of Floquet’s theory.

Our objective is to provide a comprehensive framework that facilitates a clearer discussion of novel aspects, with particular emphasis on implementation details able to ensure the reproducibility of the procedure.

2.1 State-space formulation

A dynamical system can be formally defined as a combination of a state space \({\mathcal {X}}\), a set of times \({\mathcal {T}}\), and a rule \({\mathcal {R}}\) that defines how the system’s state evolves in time [26, 27]. Hysteretic mechanical systems subjected to time-periodic inputs also belong to this general framework. In particular, such systems are governed by a set of first-order nonautonomous ODEs in the form:

$$\begin{aligned} \dot{{\textbf {x}}} = {\textbf {F}} \left( {\textbf {x}},t,\varOmega \right) , \end{aligned}$$
(1)

where t represents time, \({\textbf {x}}\) denotes the state vector containing the system’s state variables, \({\textbf {F}}\) represents a typically nondifferentiable vector field determined by the problem, and the control parameter \(\varOmega \), referred to as the continuation parameter, corresponds to the angular frequency of the input.

To analyze the behavior of Eq. (1), the governing ODEs can be reformulated, by introducing an additional state variable and a rule of variation that includes the time dependence (see “Appendix A”), as a system of first-order autonomous ODEs:

$$\begin{aligned} \dot{{\textbf {x}}} = {\textbf {f}} \left( {\textbf {x}},\varOmega \right) . \end{aligned}$$
(2)

Please notice that Eqs. (1) and (2) contain a slight abuse of notation since the same symbol, e.g., \({\textbf {x}}\), is used to denote vectors having different dimension, as much as the vector fields \({\textbf {F}}\) and \({\textbf {f}}\).

2.2 How to find periodic solutions

Fig. 1
figure 1

Graphical representation of the first return map for a 2D nonautonomous system periodic in time with period T

Full size image

Computing periodic solutions for hysteretic mechanical systems under time-periodic inputs is a highly challenging task. However, in the case of the n-dimensional hysteretic mechanical systems described by Eq. (2), the period associated with a periodic orbit can be explicitly determined. This is due to the fact that the vector field \({\textbf {f}}\) exhibits periodicity with a period \(T=\frac{2\pi }{\varOmega }\). As a result, a periodic solution of Eq. (2) will have a period that is either an integer multiple or an integer submultiple of T. The knowledge of this period can be used, as shown in the sequel, to construct a Poincaré section, enabling the mapping of intersecting points after a specific return period \(T^{j } = \text {j} T\) [28, 29].

A Poincaré section is a hypersurface in the state-space defined as:

$$\begin{aligned} \varSigma {:}{=}\left\{ {\textbf {x}} \in {\mathbb {R}}^{n -1} \times {\mathbb {S}}: x_{n} = \text {j} \frac{2\pi }{T}(t-t_{0})\right\} , \end{aligned}$$
(3)

where \(x_{n} = \varOmega t\) (mod \(2\pi \)) is the additional state variable introduced to deal with time dependence. Moreover, the space to which the state variables belong is a cylindrical space written as \( {\mathbb {R}}^{n -1} \times {\mathbb {S}}\) [29].

The hypersurface \(\varSigma \) of dimension \((n-1)\) must be chosen to ensure that the flow defined by Eq. (2) is everywhere transversal to \(\varSigma \) [30], that is:

$$\begin{aligned} {\textbf {n}}\left( {\textbf {x}}\right) \cdot {\textbf {f}}\left( {\textbf {x}},\varOmega \right) \ne 0 \quad \forall {\textbf {x}} \in \varSigma , \end{aligned}$$
(4)

where \({\textbf {n}}\left( {\textbf {x}} \right) \) represents the unit vector normal to the Poincaré section \(\varSigma \) at point \({\textbf {x}}\).

To obtain a global section (transverse to the flow everywhere in the state space) the \((n\times 1)\) normal vector \({\textbf {n}}({\textbf {x}})\) is defined as:

$$\begin{aligned} {\textbf {n}}({\textbf {x}}) {:}{=}\left[ \begin{matrix} 0\\ \vdots \\ 0\\ 1 \end{matrix} \right] \quad \forall {\textbf {x}}\in {\mathbb {R}}^{n -1} \times {\mathbb {S}}. \end{aligned}$$
(5)

It is now possible to introduce a Poincaré map based on the return time \(T^{j }\) as the value that the trajectory having \(\tilde{{\textbf {x}}} \in \varSigma \) as its initial point at time \(t_{0}\) takes on when \(t=t_0+T^{j }\). In other words, we can express the Poincaré map as:

$$\begin{aligned} {\textbf {P}}^{j }\left( {\textbf {x}},\varOmega \right) :\varSigma\rightarrow & {} \varSigma \nonumber \\{} & {} \qquad {\textbf {P}}^{j }\left( \tilde{{\textbf {x}}}, \varOmega \right) = \varvec{\varphi } \left( \tilde{{\textbf {x}}}, t_{0}, t_{0}+T^{j } \right) . \nonumber \\ \end{aligned}$$
(6)

Hence, assuming that a specific point \(\varvec{\eta } \in \varSigma \) is a fixed point of the first return map \({\textbf {P}}\left( \varvec{\eta },\varOmega \right) \), then all trajectories starting from \(\varvec{\eta }\) return to the same point after a period T, which is equal to the period of the input (Fig. 1). This condition, called fixed-point condition, can then be written as follows:

$$\begin{aligned} {\textbf {P}}\left( \varvec{\eta },\varOmega \right) = \varvec{\eta }, \end{aligned}$$
(7)

and a periodic solution can be found as a solution of the fixed-point equation:

$$\begin{aligned} {\textbf {P}}\left( \varvec{\eta },\varOmega \right) - \varvec{\eta } = {\textbf {0}}. \end{aligned}$$
(8)

This is conceptually simpler than searching for periodic solution, but it requires refined numerical tools to solve the problem. Moreover, since most of the problems of interest do not have a closed-form expression for the Poincaré map, it is necessary to rely on approximate methods or simulations instead of analytical solutions.

2.3 How to solve the fixed-point equation

When strong nonlinearities are involved, numerical techniques such as continuation become necessary to solve the fixed-point equation. This is especially true in the case of hysteretic mechanical systems since a time-periodic input can cause different behavior depending on the frequency of the applied loading.

Basically a continuation scheme is a numerical algorithm that starts with a known solution point for the fixed-point equation, indicated as \((\varvec{\eta }_{0},\varOmega _{0})\), and proceeds to compute discrete points along the solution branch that originates from \((\varvec{\eta }_{0},\varOmega _{0})\). Hence, the two basic steps of a continuation scheme are:

  1. 1.

    A predictor step to generate an initial guess of a new solution point \((\varvec{\eta }^{(1)}, \varOmega ^{(1)})\) near the last converged solution point.

  2. 2.

    An iterative correction algorithm designed to successively update and improve the initial guess until some convergence criterion is met.

Perhaps the most popular solution algorithm with these capabilities is the pseudo-arclength continuation scheme [28, 31, 32].

Fig. 2
figure 2

Graphical representation of the pseudo-arclength scheme in the case of 3D \(\left( \varvec{\eta },\varOmega \right) \)-space

Full size image

2.3.1 Pseudo-arclength continuation method

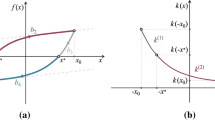
The pseudo-arclength method describes the solution path defined by Eq. (8) incrementally, using a sequence of arclength increments \(\varDelta s\). The main idea is to extrapolate a distance of \(\varDelta s\) in the \(\left( \varvec{\eta },\varOmega \right) \)-space from the known solution point \(\left( \varvec{\eta }_{0},\varOmega _{0}\right) \) along the tangent vector \({\textbf {a}}\) at the known solution point. This serves as a prediction, but then a numerical method is performed to get back onto the solution branch, as shown in [33], individuated by its intersection with the plane perpendicular to \({\textbf {a}}\) at a distance of \(\varDelta s\). Figure 2 shows a representation of the pseudo-arclength continuation method where s denotes the arclength along the solution curve.

Expressing both the periodic solution \(\varvec{\eta }\) and the continuation parameter \(\varOmega \) as functions of the coordinate s, the number of unknowns is increased by one and Eq. (8) is reparameterized as:

$$\begin{aligned} {\textbf {P}}\left( \varvec{\eta }(s),\varOmega (s) \right) - \varvec{\eta }(s) = {\textbf {0}}. \end{aligned}$$
(9)

The initial prediction, evaluated by means of a linear extrapolation along the unit tangent direction \({\textbf {a}}\), is:

$$\begin{aligned} \left[ \begin{array}{ll} \varvec{\eta }^{(1)}\\ \varOmega ^{(1)} \end{array} \right] = \left[ \begin{array}{ll} \varvec{\eta }_{0}\\ \varOmega _{0} \end{array} \right] + {\textbf {a}}\varDelta s, \end{aligned}$$
(10)

where the unit tangent vector is:

$$\begin{aligned} {\textbf {a}} = \left[ \frac{\partial \varvec{\eta }_{0}}{\partial s}, \frac{\partial \varOmega _{0}}{\partial s}\right] ^T . \end{aligned}$$
(11)

The updated equilibrium solution is sought as the intersection between the plane perpendicular to the unit tangent vector \({\textbf {a}}\) passing through the initial prediction \((\varvec{\eta }^{(1)}, \varOmega ^{(1)})\) and the solution curve.

Denoting by \({\textbf {b}}\) the vector normal to the tangent vector \({\textbf {a}}\) passing through \((\varvec{\eta }^{(1)}, \varOmega ^{(1)})\), the updated state of the system \(\left( \varvec{\eta }(s),\varOmega (s) \right) \) is sought as the solution of the fixed-point equation, e.g., Eq. (9), subjected to the orthogonality condition \({\textbf {b}} \cdot {\textbf {a}} = 0\). Hence, one has to solve the following nonlinear equation:

$$\begin{aligned} \begin{aligned} g&\left( \varvec{\eta }(s),\varOmega (s) \right) =\\&=\left[ \varvec{\eta }(s) - \varvec{\eta }_{0} \right] \cdot \frac{\partial \varvec{\eta }_{0}}{\partial s} + \left[ \varOmega (s) - \varOmega _{0} \right] \frac{\partial \varOmega _{0}}{\partial s} - \varDelta s = 0. \end{aligned} \end{aligned}$$
(12)

Based on the known solution point \(\left( \varvec{\eta }_{0},\varOmega _{0}\right) \), and given the \(\varDelta s\) increment, the solution of the augmented system is sought as a solution of the following system:

$$\begin{aligned} \left\{ \begin{array}{l} {\textbf {P}}\left( \varvec{\eta }(s),\varOmega (s) \right) - \varvec{\eta }(s) = {\textbf {0}} \\ g \left( \varvec{\eta }(s),\varOmega (s) \right) = 0. \end{array} \right. \end{aligned}$$
(13)

To solve the system of nonlinear equations obtained in Eq. (13), several methods can be used, as shown in [33,34,35]. The most classical one, used for example in [24, 25, 36], is the Newton-Raphson method.

2.3.2 Newton–Raphson method

According to the Newton–Raphson method, at the k-th iteration, one sets:

$$\begin{aligned} \varvec{\eta }^(k)= & {} \varvec{\eta }^(k-1) + \varDelta \varvec{\eta }^(k) ,\end{aligned}$$
(14)
$$\begin{aligned} \varOmega ^(k)= & {} \varOmega ^(k-1) + \varDelta \varOmega ^(k) , \end{aligned}$$
(15)

into Eq. (13) so that a Taylor expansion about \((\varvec{\eta }^(k-1) , \varOmega ^(k-1) )\) yields the incremental linearized equations in matrix form:

$$\begin{aligned} {\textbf {J}}^(k-1) \varDelta {\textbf {z}}^(k) = - {\textbf {r}}^(k-1) , \end{aligned}$$
(16)

where the notation (k-1) indicates that the scalar and matrix-valued functions are evaluated at \((\varvec{\eta }^(k-1) , \varOmega ^(k-1) )\). In particular, the augmented unknown vector and the augmented residual vector are given, respectively, by:

$$\begin{aligned} \begin{aligned} \varDelta {\textbf {z}}^(k)&= \left[ \begin{matrix} \varDelta \varvec{\eta }^(k) \\ \varDelta \varOmega ^(k) \end{matrix} \right] , \\ {\textbf {r}}^(k-1)&= \left[ \begin{matrix} {\textbf {P}}\left( \varvec{\eta }^(k-1) ,\varOmega ^(k-1) \right) - \varvec{\eta }^(k-1) \\ g\left( \varvec{\eta }^(k-1) ,\varOmega ^(k-1) \right) \end{matrix} \right] , \end{aligned} \end{aligned}$$
(17)

while the augmented (n+1)\(\times \)(n+1) Jacobian matrix is:

$$\begin{aligned} {\textbf {J}}^(k-1) = \left[ \begin{matrix} \left( \frac{\partial {\textbf {P}}}{\partial \varvec{\eta }}- {\textbf {I}}\right) ^(k-1) &{} \left( \frac{\partial {\textbf {P}}}{\partial \varOmega }\right) ^(k-1) \\ \left( \frac{\partial \varvec{\eta }_{0}}{\partial s}\right) ^T &{} \frac{\partial \varOmega _{0}}{\partial s} \end{matrix} \right] . \end{aligned}$$
(18)

The Jacobian matrix of the Poincaré map with respect to the periodic solution \(\varvec{\eta }\) and the control parameter \(\varOmega \) is computed via a central finite-difference scheme, according to the following expressions:

$$\begin{aligned} \begin{aligned} \frac{\partial {\textbf {P}}}{\partial \varvec{\eta }} \cdot {\textbf {e}}_m&\approx \frac{{\textbf {P}}(\varvec{\eta }+\delta _{1}{} {\textbf {e}}_m , \varOmega )-{\textbf {P}}(\varvec{\eta }-\delta _{1}{} {\textbf {e}}_m , \varOmega )}{2\delta _1},\\ \frac{\partial {\textbf {P}}}{\partial \varOmega }&\approx \frac{{\textbf {P}}(\varvec{\eta }, \varOmega +\delta _{2})-{\textbf {P}}(\varvec{\eta }, \varOmega -\delta _{2})}{2\delta _2}, \end{aligned} \end{aligned}$$
(19)

where \(\delta _{1}\) and \(\delta _{2}\) are the finite differences in the two gradients computations, respectively, and \({\textbf {e}}_m \) is the m-th column of the (n\(\times \)n) identity matrix \({\textbf {I}}\).

Since the Jacobian \({\textbf {J}}\) is generally nonsingular [28], the solution can be determined as:

$$\begin{aligned} \varDelta {\textbf {z}}^(k) = - \left[ {\textbf {J}}^(k-1) \right] ^{-1} {\textbf {r}}^(k-1) . \end{aligned}$$
(20)

The iterations are continued until a suitable convergence condition is satisfied.

When the convergence is achieved, the new periodic solution on the solution curve at \(s+\varDelta s\) is assumed as the new known solution \(\left( \varvec{\eta }_{0},\varOmega _{0}\right) \).

2.3.3 Step length control

As indicated by many authors in the literature [31, 32], the basic issue of the procedure is controlling the size of the step length \(\varDelta s\). In fact, the convergence characteristics of the correction procedure vary along different parts of a solution curve. For this reason, it is important to have an adaptive step length control strategy to ensure a reasonable performance of the continuation procedure.

A common design goal for developing step length control procedures is to choose \(\varDelta s\) to maintain a certain user-defined target iteration count [32]. By prescribing an initial \(\varDelta s\) and a desired number \({\bar{k}}\) of loops to achieve convergence at the solution point, the increment \(\varDelta s^(k+1) \) at the (k+1)-th solution step is set based on the number of iterations \(k^{\star }\) actually needed for the convergence at the k-th solution step, according to the general formula:

$$\begin{aligned} \varDelta s^(k+1) = \rho ^(k) \varDelta s^(k) , \ \varDelta s^(k+1) \in \left[ \varDelta s_min , \varDelta s_max \right] , \end{aligned}$$
(21)

where \(\rho ^(k) \) is a coefficient that corrects the step \(\varDelta s\) depending on the assigned law. For example, Riks in [31] proposed:

$$\begin{aligned} \rho ^(k) {:}{=}\left( \frac{\bar{k}}{k^{\star }}\right) ^{0.5}. \end{aligned}$$
(22)

This value provides good results, although it tends to maintain an excessively small step in some portions of the solution curve. More recently, Formica et al. in [33] proposed the following expression for the coefficient \(\rho ^(k) \):

$$\begin{aligned} \rho ^(k) {:}{=}\left( 1 + \frac{{\bar{k}}-k^{\star }}{{\bar{k}}+k^m } \right) , \end{aligned}$$
(23)

where \(k^m \) is the maximum number of admissible iteration loops. Such an expression, as shown in [33], provides excellent computational times.

Fig. 3
figure 3

Dimensional (a) and Non-dimensional (b) SDoF hysteretic mechanical systems

Full size image

2.4 Determine stability and bifurcation

An additional advantage of the described procedure is the possibility of using Poincaré maps to determine the stability and bifurcation of a periodic solution by analyzing its behavior near a fixed-point (Floquet’s theory) [28, 29]. After achieving convergence, the procedure furnishes the Jacobian matrix evaluated at the periodic solution (i.e., the so-called monodromy matrix \(\varvec{\Phi }\)):

$$\begin{aligned} \varvec{\Phi } = \frac{\partial {\textbf {P}}}{\partial \varvec{\eta }}. \end{aligned}$$

The eigenvalues of the monodromy matrix \(\varvec{\Phi }\), known as Floquet multipliers, allow us to ascertain the stability of the calculated orbit and its bifurcations.

3 Equations of motion

This section focuses on formulating the nonlinear equations of motion for a general class of SDoF hysteretic mechanical systems. Initially, we derive these equations in their dimensional form. Subsequently, we follow a systematic procedure consisting of five steps to obtain the non-dimensional form for the system of interest and a non-dimensional version of the VRM+D for the evaluation of the hysteretic variable.

3.1 Dimensional system

The dimensional SDoF hysteretic mechanical system (shown in Fig. 3a) consists of a mass m connected in parallel to three distinct types of elements:

  • a linear elastic spring;

  • a linear rate-dependent hysteretic element;

  • a rate-independent hysteretic spring.

Denoting by u, \({\dot{u}}\) and \(\ddot{u}\) the generalized displacement, velocity and acceleration, respectively, the dimensional equation of motion of the SDoF hysteretic mechanical system (Fig. 3a) can be derived from the general form of the Newton’s second law as:

$$\begin{aligned} m\ddot{u}+c{\dot{u}}+ku+f_{ri} = p_{0} \cos \left( 2\pi f_{p} t \right) , \end{aligned}$$
(24)

where c is the viscous damping coefficient, k is the stiffness of the elastic spring, \(f_{ri}\) is the generalized rate-independent hysteretic force exerted on the hysteretic element, whereas \(p_{0}\) (\(f_{p}\)) is the amplitude (frequency) of the input force.

Table 1 Dimensional VRM+D parameters adopted to simulate the hysteresis loops in Fig. 4
Full size table
Table 2 Non-dimensional VRM+D parameters adopted to simulate the hysteresis loops in Fig. 5
Full size table

According to the VRM+D [18] the generalized rate-independent hysteretic force \(f_{ri}\) in Eq. (24) is governed by the following ODE:

$$\begin{aligned}{} & {} {\dot{f}}_{ri} = \left\{ k_{e}\left( u\right) + k_{b} +\alpha f_{0} \right. +\nonumber \\{} & {} \left. + s\alpha \left[ f_{e}\left( u\right) {+} k_{b}u{-}f_{ri}\right] \right\} {\dot{u}},\nonumber \\ \end{aligned}$$
(25)

where \(s{:}{=}\text {sgn}\left( {\dot{u}}\right) \), and the generalized function \(k_{e}\) is given by:

$$\begin{aligned} k_{e}\left( u\right) = \beta _{1}\beta _{2}e^{\beta _{2}u}+4\gamma _{1}\gamma _{2}\frac{e^{-\gamma _{2}\left( u-\gamma _{3}\right) }}{\left[ 1+e^{-\gamma _{2}\left( u-\gamma _{3}\right) }\right] ^{2}}. \end{aligned}$$
(26)

Similarly, the generalized function \(f_{e}\) is given by:

$$\begin{aligned} f_{e}\left( u\right) = \beta _{1}\left( e^{\beta _{2}u}-1\right) +2\gamma _{1}\frac{1-e^{-\gamma _{2}\left( u-\gamma _{3}\right) }}{1+e^{-\gamma _{2}\left( u-\gamma _{3}\right) }}. \end{aligned}$$
(27)

In Eq. (25), the model parameters can be updated depending on the sign of the velocity \({\dot{u}}\). In particular, \(k_{b}=k_{b}^{+}\left( k_{b}^{-}\right) \), \(f_{0}=f_{0}^{+}\left( f_{0}^{-}\right) \), \(\alpha =\alpha ^{+}\left( \alpha ^{-}\right) \), \(\beta _{1}=\beta _{1}^{+}\left( \beta _{1}^{-}\right) \), \(\beta _{2}=\beta _{2}^{+}\left( \beta _{2}^{-}\right) \), \(\gamma _{1}=\gamma _{1}^{+}\left( \gamma _{1}^{-}\right) \), \(\gamma _{2}=\gamma _{2}^{+}\left( \gamma _{2}^{-}\right) \), \(\gamma _{3}=\gamma _{3}^{+}\left( \gamma _{3}^{-}\right) \) if \(s >0 \) \(\left( s <0\right) \). For the mechanical interpretation of the previous coefficients the reader is referred to [17, 18].

3.2 Non-dimensionalization

Non-dimensionalization is a fundamental technique employed in the analysis of systems governed by ODEs. There are many reasons for using such a technique. Firstly, this approach simplifies the problem by reducing the number of the involved parameters. This simplification makes it easier to analyze and grasp the relationship between the parameters of the system. Secondly, non-dimensionalization allows for the comparison of different systems with varying physical parameters on the same scale, facilitating the identification of common trends and properties across different systems. Moreover, it helps to eliminate the units of measurement, making the problem more general and independent of specific units [37].

Although there are several approaches to non-dimensionalize an equation, see, e.g., [37], the non-dimensionalization procedure can be systematically divided into five distinct steps. These sequential steps include: (i) identifying all independent and dependent variables; (ii) replacing all variables with non-dimensional quantities based on characteristic units; (iii) dividing the obtained equation by the coefficient of the highest-order derivative; (iv) selecting the characteristic unit for each variable so that potential auxiliary conditions become as simple as possible; (v) rewriting the equation in terms of new dimensionless quantities.

By applying these steps to the system of differential equations represented by Eqs. (24) and (25), we have that:

  1. (i)

    The independent variable is the time t, whereas the generalized displacement u, and the generalized rate-independent hysteretic force \(f_{ri}\) are the dependent variables.

  2. (ii)

    We introduce as non-dimensional variables:

    $$\begin{aligned} \tau {:}{=}\frac{t - t_{r}}{t_{s}}, \ \ x {:}{=}\frac{u - u_{r}}{u_{s}}, \ \ z {:}{=}\frac{f_{ri} - f_{r}}{f_{s}}. \end{aligned}$$
    (28)

    These quantities are defined as the difference between the dimensional variable and a reference value (i.e., \(t_{r}\), \(u_{r}\) and \(f_{r}\)), scaled by a dimensional scaling factor (i.e., \(t_{s}\), \(u_{s}\) and \(f_{s}\)). Based on these definitions, the dimensional variables can be expressed as follows:

    $$\begin{aligned}{} & {} t = t_{s}\tau + t_{r}, \nonumber \\{} & {} u = u_{s}x + u_{r}, \nonumber \\{} & {} f_{ri} = f_{s}z +f_{r}. \end{aligned}$$
    (29)

    Now it is possible to replace the dimensional variables in Eqs. (24) and (25) with the non-dimensional ones, by using Eq. (29). In particular, we obtain for Eq. (24):

    $$\begin{aligned} \begin{aligned} \frac{mu_{s}}{t_{s}^{2}}&\frac{d^{2}x}{d\tau ^{2}}+\frac{cu_{s}}{t_{s}}\frac{dx}{d\tau }+k\left( u_{s}x + u_{r}\right) + \\&+\left( f_{s}z + f_{r}\right) = p_{0} \cos \left[ 2\pi f_{p} \left( t_{s}\tau + t_{r}\right) \right] . \end{aligned} \end{aligned}$$
    (30)

    On the other hand, if we plug Eqs. (29) into (25), we obtain:

    $$\begin{aligned}{} & {} \frac{f_{s}}{t_{s}}\frac{dz}{d\tau } = \left\{ k_{e}\left( u_{s}x + u_{r}\right) + k_{b} + \alpha f_{0} +\right. \nonumber \\{} & {} \text {sgn} \left( \frac{u_{s}}{t_{s}}\frac{dx}{d\tau } \right) \alpha \left. \left[ f_{e}\left( u_{s}x {+} u_{r}\right) {+} k_{b}\left( u_{s}x {+}u_{r}\right) {+}\right. \right. \nonumber \\{} & {} \left. \left. -\left( f_{s}z + f_{r}\right) \right] \right\} \frac{u_{s}}{t_{s}}\frac{dx}{d\tau }. \end{aligned}$$
    (31)
  3. (iii)

    The coefficients of the highest-order term in Eqs. (30) and (31) are \(\frac{mu_{s}}{t_{s}^{2}}\) and \(\frac{f_{s}}{t_{s}}\), respectively. Hence, upon dividing Eqs. (30) by \(\frac{mu_{s}}{t_{s}^{2}}\) and (31) by \(\frac{f_{s}}{t_{s}}\), one obtains:

    $$\begin{aligned} \begin{aligned}&\ddot{x}+\frac{ct_{s}}{m}{\dot{x}}+\frac{kt_{s}^{2}}{m}x +\frac{f_{s}t_{s}^{2}}{mu_{s}}z + \frac{t_{s}^{2}}{mu_{s}} \\&\left( ku_{r} + f_{r}\right) = \frac{p_{0}t_{s}^{2}}{mu_{s}} \cos \left[ 2\pi f_{p} \left( t_{s}\tau + t_{r}\right) \right] , \end{aligned} \end{aligned}$$
    (32)

    and

    $$\begin{aligned}{} & {} {\dot{z}} = \frac{u_{s}}{f_{s}} \left\{ k_{e}\left( u_{s}x + u_{r}\right) + k_{b} + \alpha f_{0} +\right. \nonumber \\{} & {} \text {sgn} \left( \frac{u_{s}}{t_{s}}{\dot{x}} \right) \alpha \left. \left[ f_{e}\left( u_{s}x + u_{r}\right) + k_{b}\left( u_{s}x + u_{r}\right) + \right. \right. \nonumber \\{} & {} \left. \left. -\left( f_{s}z + f_{r}\right) \right] \right\} {\dot{x}}, \end{aligned}$$
    (33)

    where the superimposed dot now represents the derivative with respect to the non-dimensional time \(\tau \).

  4. (iv)

    To simplify the final dimensionless expressions as much as possible, we impose that the reference values \(t_{r}\), \( u_{r}\), \( f_{r}\) are equal to zero. In this way we obtain:

    $$\begin{aligned} \ddot{x}+\frac{ct_{s}}{m}{\dot{x}}+\frac{kt_{s}^{2}}{m}x +\frac{f_{s}t_{s}^{2}}{mu_{s}}z = \frac{p_{0}t_{s}^{2}}{mu_{s}} \cos \left( 2\pi f_{p} t_{s}\tau \right) ,\nonumber \\ \end{aligned}$$
    (34)

    and

    $$\begin{aligned} {\dot{z}} = \frac{u_{s}}{f_{s}} \left\{ k_{e}\left( u_{s}x\right) + k_{b} + \alpha f_{0} +\right. \text {sgn} \left( \frac{u_{s}}{t_{s}}{\dot{x}} \right) \nonumber \\ \left. \alpha \left[ f_{e}\left( u_{s}x\right) + k_{b}u_{s}x -f_{s}z \right] \right\} {\dot{x}}. \end{aligned}$$
    (35)

    Thus, it is only necessary to determine the scaling factors \(t_{s}\), \(u_{s}\) and \(f_{s}\) so that Eqs. (34) and (35), and potential auxiliary conditions, become as simple as possible. One possible choice is to set the coefficients in front of x and z in Eq. (34) equal to one:

    $$\begin{aligned} \frac{kt_{s}^{2}}{m}= & {} 1 \rightarrow t_{s} = \sqrt{\frac{m}{k}},\end{aligned}$$
    (36)
    $$\begin{aligned} \frac{f_{s}t_{s}^{2}}{mu_{s}}= & {} 1 \rightarrow k = \frac{f_{s}}{u_{s}}. \end{aligned}$$
    (37)

    A further assumption concerning Eq. (35) can be made by requiring that:

    $$\begin{aligned} \text {sgn} \left( \frac{u_{s}}{t_{s}}{\dot{x}} \right) = \text {sgn} \left( {\dot{u}} \right) \Rightarrow \frac{u_{s}}{t_{s}}>0. \end{aligned}$$
    (38)

    Let \(\alpha ^{+} = \alpha ^{-} = \alpha \) and \(f_{0}^{+} = f_{0}^{-} = f_{0}\). Knowing, from the general formulation of the model by Vaiana and Rosati [17, 18], that \(\alpha > 0\), and imposing that \(f_{0} >0\), we can define the scaling factors as:

    $$\begin{aligned} u_{s} {:}{=}\frac{1}{\alpha }, \quad f_{s} {:}{=}f_{0}, \end{aligned}$$
    (39)

    so as to obtain:

    $$\begin{aligned} \frac{u_{s}}{t_{s}} = \sqrt{\frac{f_{0}}{\alpha m}} > 0. \end{aligned}$$
    (40)

    As a result, the other non-dimensional coefficients are defined as follows:

    $$\begin{aligned} 2\zeta&{:}{=}&\frac{ct_{s}}{m} = \frac{c}{\sqrt{mk}},\end{aligned}$$
    (41)
    $$\begin{aligned} F&{:}{=}&\frac{p_{0}t_{s}^{2}}{mu_{s}} = \frac{p_{0}}{f_{0}},\end{aligned}$$
    (42)
    $$\begin{aligned} \varOmega&{:}{=}&2\pi f_{p} t_{s} = 2\pi f_{p}\sqrt{\frac{m}{k}}. \end{aligned}$$
    (43)
  5. (v)

    The final non-dimensional SDoF hysteretic mechanical system (see Fig. 3b) is ruled by the following ODEs:

    $$\begin{aligned} \ddot{x}+2\zeta {\dot{x}}+x +z = F \cos \left( \varOmega \tau \right) , \end{aligned}$$
    (44)

    and

    $$\begin{aligned}{} & {} {\dot{z}} = \left\{ \frac{k_{e}\left( \frac{x}{\alpha }\right) }{f_{0}\alpha } + \frac{k_{b}}{f_{0}\alpha } + 1 +\right. \nonumber \\{} & {} \left. \left[ \frac{f_{e}\left( \frac{x}{\alpha }\right) }{f_{0}} + \frac{k_{b}}{f_{0}\alpha }x-z\right] \right\} {\dot{u}}.\nonumber \\ \end{aligned}$$
    (45)
Fig. 4
figure 4

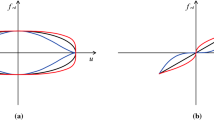
Dimensional hysteresis loops simulated by using the VRM+D parameters in Table 1

Full size image
Fig. 5
figure 5

Non-dimensional hysteresis loops simulated by using the VRM+D parameters in Table 2

Full size image

3.2.1 Non-dimensional VRM+D

The non-dimensional form of the VRM+D in Eq. (45) can be further simplified if we define two new non-dimensional functions:

$$\begin{aligned} \kappa _{e}\left( x\right) {:}{=}\frac{k_{e}\left( \frac{x}{\alpha }\right) }{f_{0}\alpha } \quad \text {and} \quad \phi _{e}\left( x\right) {:}{=}\frac{f_{e}\left( \frac{x}{\alpha }\right) }{f_{0}}. \end{aligned}$$
(46)

Along with these non-dimensional functions, we can define six non-dimensional model parameters such as:

$$\begin{aligned} \begin{aligned}&\chi _{1} {:}{=}\frac{\beta _{1}}{f_{0}}, \quad \chi _{2} {:}{=}\frac{\beta _{2}}{\alpha }, \quad \chi _{3} {:}{=}\frac{2\gamma _{1}}{f_{0}}, \\&\chi _{4} {:}{=}\frac{\gamma _{2}}{\alpha }, \quad \chi _{5} {:}{=}\alpha \gamma _{3}, \quad \chi _{6} {:}{=}\frac{k_{b}}{f_{0}\alpha }. \end{aligned} \end{aligned}$$
(47)

Some of these quantities appear in the non-dimensional function \(\kappa _{e}\left( x\right) \):

$$\begin{aligned} \kappa _{e}\left( x\right) = \chi _{1}\chi _{2}e^{\chi _{2}x}+ 2 \chi _{3}\chi _{4}\frac{e^{-\chi _{4}\left( x-\chi _{5}\right) }}{\left[ 1+e^{-\chi _{4}\left( x-\chi _{5}\right) }\right] ^{2}}, \end{aligned}$$
(48)

and in the non-dimensional function \(\phi _{e}\left( x\right) \):

$$\begin{aligned} \phi _{e}\left( x\right) = \chi _{1}\left( e^{\chi _{2}x}-1\right) +\chi _{3}\frac{1-e^{-\chi _{4}\left( x-\chi _{5}\right) }}{1+e^{-\chi _{4}\left( x-\chi _{5}\right) }}. \end{aligned}$$
(49)

Finally, the general form of the non-dimensional VRM+D can be expressed as follows:

$$\begin{aligned} {\dot{z}} = \left\{ \kappa _{e}\left( x\right) + \chi _{6} + 1 + s \left[ \phi _{e}\left( x\right) + \chi _{6}x-z\right] \right\} {\dot{x}}. \end{aligned}$$
(50)

It is worth noting that the non-dimensionalization led to a reduction in the number of parameters upon which the hysteretic mechanical system is dependent, from 21 in the model depicted in Fig. 3a to 15 in the one illustrated in Fig. 3b.

On account of the reduced number of parameters in the non-dimensional model, it is natural to ask whether some information has been lost in the description of the system behavior, an issue that, to the best of our knowledge, has not been addressed in the specialized literature. For this reason, we have decided to compare the loop shapes predicted by the dimensional and non-dimensional form of the VRM+D. Specifically, by using the dimensional parameters given in Table 1 and imposing a sinusoidal generalized displacement having an amplitude of 1.5 m and a frequency of 1 Hz, we obtained the dimensional hysteresis loops in Fig. 4.

On the other hand, for the non-dimensional model, it is easy to derive the non-dimensional parameters listed in Table 2 by applying Eq. (47). These parameters are used in Eq. (50) to derive the non-dimensional hysteresis loops in Fig. 5. It is important to note that for both dimensional and non-dimensional loops, the classification proposed in [17] does apply. In fact, according to their proposal hysteresis loops can be classified into four main categories:

  • Shape type S1: Characterized by hysteresis loops limited by two straight lines (Figs. 4a and 5a).

  • Shape type S2: Characterized by hysteresis loops limited by two curves with no inflection point (Figs. 4b and 5b).

  • Shape type S3: Characterized by hysteresis loops limited by two curves with one inflection point (Figs. 4c and 5c).

  • Shape type S4: Characterized by hysteresis loops limited by two curves with two inflection points (Figs. 4d and 5d).

In the sequel, we shall derive the frequency-response curves for the four categories of loop shapes.

4 Frequency-response curves: stability and bifurcations

Fig. 6
figure 6

FRCs for SDoF hysteretic mechanical systems having S1 (a), S2 (b), S3 (c), S4 (d) hysteresis loops and different amplitudes F of the input force

Full size image
Table 3 Parameters used for the pseudo-arclength path following procedure
Full size table
Fig. 7
figure 7

Validation of the results in Fig. 6 through NLTHAs (dot markers) for different amplitudes F of the input force

Full size image
Fig. 8
figure 8

System S1: FRC assuming as amplitude of the input force \(F=1.2\) (a) and periodic orbit in the state-space at \(\varOmega =1.01725\) (b)

Full size image
Fig. 9
figure 9

Enlarged views of the FRCs in Fig. 6b (system S2) assuming as amplitude of the input force \(F=10.0\) (a) and \(F=30.0\) (b)

Full size image
Fig. 10
figure 10

System S2: FRC assuming as amplitude of the input force \(F=2.0\) (a) and periodic orbits in the state-space at \(\varOmega =1.05\) (b)

Full size image
Fig. 11
figure 11

System S3: FRC assuming as amplitude of the input force \(F=1.2\) (a) and periodic orbits in the state-space at \(\varOmega =1.01724\) (b)

Full size image
Fig. 12
figure 12

Enlarged views of the FRCs in Fig. 6d (system S4) assuming as amplitude of the input force \(F=1.0,\ 2.0, \ 3.0\) (a), \(F=10.0\) (b) and \(F=20.0\) (c)–(d)

Full size image
Fig. 13
figure 13

System S4: FRC assuming as amplitude of the input force \(F=3.0\) (a) and periodic orbits in the state-space at \(\varOmega =1.3214\) (b)

Full size image
Fig. 14
figure 14

System S4: FRCs in terms of maximum velocity (a), acceleration (b), transmitted force (c), and normalized transmitted force (d) for different amplitudes F of the input force

Full size image

In this section, we discuss a comprehensive examination of the Frequency-Response Curves (FRCs) of four SDoF hysteretic mechanical systems subjected to time-periodic input. The assumed hysteretic behaviors are the ones previously described in Sect. 3.2.1 and depicted in Fig. 5. This comprehensive analysis provides valuable insights into the stability and bifurcation characteristics of the analyzed systems.

The results are organized in order to improve readability. First, the analyzed systems and the methodologies used are described. Next, the results are grouped according to loop shape typology, and for each shape, a detailed description of the FRCs obtained for different amplitudes of the input is provided, along with stability and bifurcation indications. Finally, for each system, significant points of the FRCs are represented in state-space in order to comment on specific results for particular amplitudes and angular frequencies.

Furthermore, for the hysteresis loop S4 in Fig. 5d, four additional FRCs are provided. These additional curves are expressed in terms of maximum velocity, acceleration, transmitted force and normalized transmitted force, which can be useful in various engineering applications.

We analyze the hysteretic mechanical system depicted in Fig. 3b with four different hysteretic laws, namely those whose loop shapes are obtained by applying the parameters listed in Table 2. Each system is defined by Eqs. (44) and (50), with the additional condition \(\zeta =0\).

4.1 Description of the analyzed systems

The four SDoF hysteretic mechanical systems under analysis are:

  1. 1.

    System S1: In the first system, both upper and lower limiting curves (red dashed lines in Figs. 4 and 5) are represented by straight lines (shape type S1). This system exhibits asymmetric behavior due to the different values of \(\chi _6^{+}\) and \(\chi _6^{-}\) while no other parameters contribute to the hysteretic behavior.

  2. 2.

    System S2: The second system has a more complex hysteretic behavior, since all parameters are different from zero. Both upper and lower limiting curves has a pronounced curvature due to the contributions of \(\chi _1\), \(\chi _2\), \(\chi _3\), \(\chi _4\), and \(\chi _5\) but no inflection points (shape type S2). The asymmetry between the loading and unloading phases arises from distinct values of \(\chi _1\), \(\chi _2\), and \(\chi _{6}\) during each phase.

  3. 3.

    System S3: For the third system, both upper and lower limiting curves are characterized by one inflection point (shape type S3). Furthermore, this system exhibits asymmetry between upper and lower limiting curves, with different values of \(\chi _4\) and \(\chi _5\) causing the hysteresis loop to be wider in one direction than in the other.

  4. 4.

    System S4: The fourth system has a symmetric hysteresis loop shape, with both upper and lower limiting curves exhibiting two inflection points (shape type S4) and significant stiffening effects. The non-zero values of \(\chi _1\), \(\chi _2\), \(\chi _3\), and \(\chi _4\) all contribute to the complex flag-shaped behavior of this system. On the other hand, the high value of \(\chi _6\) contributes to the stiffening behavior.

4.2 Methods

We analyze the four SDoF hysteretic mechanical systems and obtain their FRCs using the procedure described in Sect. 2 (the pseudo-code can be found in “Appendix C”). The continuation parameter is \(\varOmega \), while the non-dimensional amplitude of the input force F remains constant. Furthermore, the parameters used in the procedure are listed in Table 3.

In particular, \(T/\varDelta \tau \) is the number of steps that are numerically used to evaluate the Poincaré map using the MATLAB function ode45 (“Appendix B”). The parameters \(\delta _1\) and \(\delta _2\) are introduced in Eq. (19) for the evaluation of the Jacobian matrix of the Poincaré map, and tol is the value of the tolerance imposed for the stopping criterion of the Newton–Raphson method (\(|{\textbf {r}}^(k) |<\) tol). The last four parameters in Table 3 are used for the step length control using Eqs. (21) and (23).

The procedure provides a fixed point of the Poincaré map, which is used as the initial condition to integrate Eqs. (44) and (50) again in order to obtain the FRCs shown in Fig. 6, where max|x| is plotted against \(\varOmega \), and those in Fig. 14, expressing the maximum displacement, velocity, transmitted force, and normalized transmitted force. In Figs. 6 and 14, the gray dot markers represent the maximum value for the FRC.

To determine the stability of the solutions and their bifurcations in the 3D state-space, the evolution of the three Floquet multipliers associated with the \(3\times 3\) monodromy matrix is examined. The solid lines in Figs. 6 and 14 indicate stable periodic solutions, where the magnitude of their complex-valued Floquet multipliers is less than 1. Conversely, dashed lines correspond to unstable responses for which the magnitude of at least one of the multipliers exceeds 1. In Fig. 6, red diamond markers represent the bifurcation points.

Finally, the accuracy of the periodic solutions estimated by the continuation algorithm is verified by performing Nonlinear Time History Analyses (NLTHAs), that is, directly integrating Eqs. (44) and (50), and analyzing the stable solution indicated by the dot marker in Fig. 7. In “Appendix D” additional details can be found on the number of maximum, minimum and average iterations required by the Newton–Raphson method to achieve convergence for all numerical experiments.

4.3 System S1

In the following, we present the outcomes of the investigation conducted on System S1, as described in Sect. 4.1, using different amplitudes of the input force F. The amplitudes of interest are \(0.5, \ 0.6, \ 0.8, \ 1.0, \ 1.1, \ 1.2\).

4.3.1 Frequency-response curves

For all tested levels of F, it can be observed in Fig. 6a that the FRCs are bent to the left (indicating a softening nonlinearity) and globally stable within the investigated range of F and \(\varOmega \). Specifically:

  • \(F=0.5\)

    Three resonance peaks are observed at angular frequencies of 0.282694, 0.460423, and 1.25527.

  • \(F=0.6\)

    Similarly to the previous case, three resonance peaks are observed at angular frequencies of \(0.282297\), 0.466413, and 1.22085.

  • \(F=0.8\)

    The observed resonance peaks increase to four, occurring at angular frequencies of 0.200937, 0.282297, 0.461909, and 1.14957.

  • \(F=1.0\)

    As in the previous case, four resonance peaks are observed at angular frequencies of 0.200095, 0.279511, 0.455687, and 1.07779.

  • \(F=1.1\)

    Four resonance peaks are still present, but they occur within an angular frequencies range of \(\left( 0.15, \ 1.05 \right) \), specifically at 0.155183, 0.278341, 0.452139, and 1.04455.

  • \(F=1.2\)

    The four resonance peaks are located within the previous range, occurring at angular frequencies of 0.199027, 0.277747, 0.449525, and 1.01725. Hence, the first and last two values become closer with respect to the case \(F=1.1\), with the initial value of the first (second) pair increasing (decreasing).

4.3.2 Orbits in the state space

It is of interest to examine the state-space of the system at specific values of \(\varOmega \) and F. When \(F=1.2\) and \(\varOmega =1.01725\), corresponding to the fourth resonance peak, there is only one intersection with the FRC in Fig. 8a. This intersection indicates the existence of a unique stable periodic solution for the system, with a maximum displacement (\(\max |x|\)) equal to 16.6649.

Figure 8b shows the shape of the periodic orbit in the state-space, as well as its projections onto the planes \((x,\ {\dot{x}})\), \((x, \ z)\), and \(({\dot{x}}, \ z)\). The figure also includes the fixed point provided by the procedure (red dot) and the point corresponding to the maximum displacement reported in the FRC (gray dot).

4.4 System S2

In the sequel, we present the results obtained from the analysis of the System S2, as described in Sect. 4.1, under different values of amplitudes for the input force F, that are \(1.0, \ 2.0, \ 3.0, \ 10.0, \ 20.0, \ 30.0\).

4.4.1 Frequency-response curves

Making reference to the FRCs in Fig. 6b one has:

  • \(F = 1.0\)

    At this level of load amplitude, it can be observed that the FRC is slightly bent to the right (indicating an hardening nonlinearity) and globally stable within the investigated range of \(\varOmega \).

  • \(F = 2.0\)

    By increasing the load value, the hardening behavior of the FRC is accentuated. Furthermore, at points \(\left( 1.04927,\ 30.5508 \right) \) and \(\left( 1.05482,\ 40.2793 \right) \) the system exhibits two fold bifurcations.

  • \(F = 3.0\)

    In this case, the behavior exhibited by the curve is of the same type as the previous level of amplitude. Indeed, there is a further increase in the hardening behavior of the FRC, while the two fold bifurcations at points \(\left( 1.06602,\ 32.0483 \right) \) and \(\left( 1.08362,\ 46.3749 \right) \) move slightly away.

  • \(F = 10.0\)

    In this case, there is a further increase in the hardening behavior of the FRC. The two fold bifurcations at points \(\left( 1.15556,\ 39.3649 \right) \) and \(\left( 1.23174,\ 60.3052 \right) \) move further away. Furthermore, as shown in Fig. 9a, the FRC loses its stability at A \(\equiv \left( 0.3463,\ 11.8456 \right) \) and B \(\equiv \left( 0.346303,\ 11.7194 \right) \) due to two fold bifurcations.

  • \(F = 20.0\)

    A further increase in the amplitude modifies the bifurcation scenario, as the system exhibits two fold bifurcations at points \(\left( 1.25333,\ 44.6038 \right) \) and \(\left( 1.38267,\ 66.8305 \right) \). In addition, the unstable portion in the region of small \(\varOmega \) is lost.

  • \(F = 30.0\)

    In this last case, there is a further increase in the hardening behavior of the FRC. In particular, the two fold bifurcations at points \(\left( 1.33497,\ 47.8529 \right) \) and \(\left( 1.50612,\ 70.3138 \right) \) move further away. Moreover, as shown in Fig. 9b, the FRC loses its stability again at points C \(\equiv \left( 0.223514,\ 29.792 \right) \) and D \(\equiv \left( 0.223526,\ 29.7392 \right) \) due to two fold bifurcations.

Referring to the frequency-response curves with an amplitude of \(1.0, \ 2.0, \ 3.0\), a series of resonance peaks were observed in the range \(\varOmega \in \left( 0.1, \ 0.4\right) \). These peaks become less sharp when the force amplitude is increased.

4.4.2 Orbits in the state-space

The investigation of the state-space at specific values of \(\varOmega \) and F is a matter of interest. In particular, by observing the FRC obtained for the analyzed system for \(F=2.0\) (Fig. 10a), it can be seen that there are three intersections with the FRC at \(\varOmega =1.05\).

This indicates the existence of three periodic solutions for the system of interest: specifically, two stable orbits (labeled as a and c in Fig. 10a) and one unstable solution (labeled as b in Fig. 10a).

The shape of the periodic orbits in the state space is illustrated in Fig. 10b that also depicts the projections of the periodic orbits onto the planes \((x,\ {\dot{x}})\), \((x, \ z)\) and \(( {\dot{x}}, \ z)\) in the state space. Additionally, the orbits in Fig. 10b also include the fixed points provided by the procedure (red dots) and the points corresponding to the maximum displacement reported in the FRC (colored dots).

4.5 System S3

The following results are obtained by analyzing System S3, described in Sect. 4.1, subjected to amplitudes of the input force F equal to \(0.5, \ 0.6, \ 0.8, \ 1.0, \ 1.1, \ 1.2\).

4.5.1 Frequency-response curves

The FRCs reported in Fig. 6c show that:

  • \(F = 0.5,\ 0.6,\ 0.8,\ 1.0,\ 1.1\)

    For these amplitude of the input force, it can be observed that the FRCs are softening and globally stable within the investigated range of \(\varOmega \).

  • \(F = 1.2\)

    The FRC shows an accentuated softening behavior, and two fold bifurcations are experienced at points \(\left( 1.01689,\ 75.7157 \right) \) and \(\left( 1.01819,\ 28.0416 \right) \).

4.5.2 Orbits in the state space

Of particular interest is the exploration of the state-space at specific \(\varOmega \) and F values. In particular, by observing the FRC obtained for the system under consideration for \(F=1.2\) (Fig. 11a), it can be seen that there are three intersections with the FRC at \(\varOmega =1.01724\).

This indicates the existence of three periodic solutions for the system, specifically, two stable orbits (labeled as a and c in Fig. 11a) and a unique unstable periodic solution (labeled as b in Fig. 11a).

The shapes of the periodic orbits in state-space are illustrated in Fig. 11b, in which their projections onto the planes \((x,\ {\dot{x}})\), \((x, \ z)\), and \(( {\dot{x}}, \ z)\) are also shown. Additionally, the orbits in Fig. 11b include the fixed-points provided by the procedure (red dots) and the points corresponding to the maximum displacement reported in the FRC (colored dots).

4.6 System S4

Let us now illustrate the results obtained by analyzing System S4, as described in Sect. 4.1, under different amplitudes of the input force F equal to 1.0, 2.0, 3.0, 10.0, 20.0, 30.0.

4.6.1 Frequency-response curves

From the FRCs in Fig. 6d, one infers:

  • \(F = 1.0\)

    At this level of amplitude, the FRC exhibits a softening behavior. Additionally, the system undergoes two fold bifurcations at points \(\left( 1.54293,\ 4.61446 \right) \) and \(\left( 2.56595,\ 0.457121 \right) \). Moreover, a resonance peak is observed at an angular frequency of 1.04696 (shown in Fig. 12a).

  • \(F = 2.0\)

    For this level of amplitude, the FRC exhibits an intermediate behavior between hardening and softening. The system undergoes two fold bifurcations at points \(\left( 1.23972,\ 14.0108 \right) \) and \(\left( 2.18536,\ 0.6483 \right) \). Furthermore, as shown in Fig. 12a, the FRC loses stability at points A \(\equiv \left( 0.990398,\ 0.494804 \right) \) and B \(\equiv \left( 1.00008,\ 0.364599 \right) \) due to two fold bifurcations, as shown in Fig. 12a. Three resonance peaks are also present at the angular frequencies of 0.439879, 0.614078, and 0.990398 (shown in Fig. 12a).

  • \(F = 3.0\)

    The system exhibits an intermediate behavior between hardening and softening of the FRC. Additionally, the system undergoes a series of eight fold bifurcations (shown at points A \(\equiv \left( 1.31984,\ 19.1817 \right) \), B \(\equiv \left( 1.32162,\ 21.378 \right) \), C \(\equiv \left( 1.20139,\ 13.4231\right) \), D \(\equiv \left( 1.85713,\ 0.837714 \right) \) in Fig. 13a, while, in Fig. 12a, at C \(\equiv \left( 0.881828,\ 0.964232\right) \), D \(\equiv \left( 0.922575,\ 0.584871 \right) \), E \(\equiv \left( 0.582661,\ 0.455316\right) \), F \(\equiv \left( 0.582676,\ 0.445658 \right) \)). Finally, there are four resonance peaks corresponding to angular frequencies of 0.32768, 0.420242, 0.58274 and 0.881875 (shown in Fig. 12a).

  • \(F = 10.0\)

    For such an amplitude level, the system exhibits a fully hardening behavior of the FRC. The bifurcation scenario of the system includes two fold bifurcations at points \(\left( 1.46291,\ 20.5305 \right) \) and \(\left( 1.6029,\ 30.9474 \right) \). Additionally, the system undergoes two pitchfork bifurcations at points A \(\equiv \left( 0.610606,\ 4.48271 \right) \) (supercritical) and B \(\equiv \left( 0.567639,\ 4.21748 \right) \) (subcritical) (shown in Fig. 12b). The equilibrium paths that arise from these bifurcations are stable until points B’ \(\equiv \left( 0.567554,\ 4.24512 \right) \) and B” \(\equiv \left( 0.567562,\ 4.18991 \right) \) where they lose stability through two fold bifurcations (shown in Fig. 12b). Moreover, there are six fold bifurcations at points C \(\equiv \left( 0.45597,\ 8.23794\right) \), D \(\equiv \left( 0.445504,\ 8.01708 \right) \), E \(\equiv \left( 0.322458,\ 4.99206\right) \), F \(\equiv \left( 0.324257,\ 5.07358 \right) \), G \(\equiv \left( 0.227272,\ 6.2892 \right) \) and H \(\equiv \left( 0.22834,\ 5.7705 \right) \) in Fig. 12b.

  • \(F = 20.0\)

    At this level of amplitude, there is a further increase in the hardening behavior of the FRC. Specifically, at points \(\left( 1.61803,\ 22.4509 \right) \) and \(\left( 1.89484,\ 35.1896 \right) \), the two fold bifurcations move further apart. Additionally, as shown in Fig. 12c and d, the stability of the FRC is lost at points A \(\equiv \left( 0.433459,\ 11.8114 \right) \), B \(\equiv \left( 0.43346,\ 11.8312 \right) \), C \(\equiv \left( 0.265907,\ 16.5118 \right) \) and D \(\equiv \left( 0.265908,\ 16.4237 \right) \), due to four fold bifurcations.

  • \(F = 30.0\)

    Finally, for this amplitude level the FRC shows a hardening behavior with only two fold bifurcations at \(\left( 1.74896,\ 23.782 \right) \) and \(\left( 2.12659,\ 37.5445 \right) \).

Table 4 Coordinates of the peaks of the FRCs associated with the system S4 for different amplitudes F of the input force (Figs. 6d and 14)
Full size table

In addition to the FRCs in Fig. 6d, which represent the variation of the maximum displacement as a function of the angular frequency \(\varOmega \) for the S4 system, we have also obtained the additional FRCs shown in Fig. 14. We have not explicitly reported the analogous FRCs related to the systems S1, S2, and S3 due to space limitations and also because the S4 system, due to its peculiar features, has been considered to be worth deserving a greater attention.

In particular, once the fixed point of the Poincaré map is obtained by further integrating the equations of motion using the fixed point as the initial condition, a series of significant quantities can be obtained for the periodic orbit, such as:

  • The maximum velocity of the obtained response (Fig. 14a);

  • The maximum acceleration of the obtained response (Fig. 14b);

  • The maximum transmitted force \(f_{tot}=x+z\) (Fig. 14c);

  • The maximum normalized transmitted force  (Fig. 14d).

The stability and bifurcation behavior of the curves in Fig. 14 remain the same as previously described. However, it is noted in Table 4 that, for different amplitude levels of the input force F, the value of the angular frequency for which the maximum value is obtained in the equivalent FRC does modify.

The observation that the FRCs for other quantities such as maximum velocity, acceleration, and transmitted force are affected by the amplitude level of the input force in a different way than the maximum displacement is crucial for many engineering applications. For example, in the design of mechanical systems, it is important to consider not only the maximum displacement but also the maximum velocity and acceleration to ensure that the system does not exceed its safe operating limits. Similarly, in the analysis of civil and mechanical structures such as bridges and motors, it is important to consider the maximum transmitted force to ensure that the considered structure can withstand the loads imposed on it.

Therefore, understanding how the amplitude of the input force affects the value of the angular frequencies at which different significant quantities reach their maximum value is critical for the design and analysis of many physical systems.

4.6.2 Orbits in the state space

Examining the state-space for specific values of \(\varOmega \) and F is an intriguing prospect. In particular, by observing the FRC obtained for the system under consideration for \(F=3.0\) (Fig. 13a), it can be seen that there are five intersections with the FRC at \(\varOmega =1.3214\).

This indicates the existence of five periodic solutions for the system, specifically, three stable orbits (labeled as a, c, and e in Fig. 13a) and two unstable periodic solutions (labeled as b and d in Fig. 13a).

The shape of the periodic orbits in the state space is illustrated in Fig. 13b in which the projections of the periodic orbits onto the planes \((x,\ {\dot{x}})\), \((x,\ z)\), and \(({\dot{x}},\ z)\) are reported. Additionally, the orbits in Fig. 13b also include the fixed points provided by the procedure (red dots) and the points corresponding to the maximum displacement reported in the FRC in Fig. 13a (colored dots).

5 Conclusions

We analyzed the behavior of SDoF hysteretic mechanical systems subjected to time-periodic input by combining the hysteretic model proposed in [18] with a continuation procedure based on Poincaré maps developed in [24]. By applying this approach to different types of hysteresis loop shapes, we have shown its effectiveness in accurately predicting the behavior of complex mechanical systems, including their steady-state response, stability and bifurcation.

In particular, the bifurcation analysis provides valuable information on the dynamics of the system under different loading conditions and can help in the design of control strategies to mitigate undesired effects related to hysteresis.

For these reasons, further studies will be conducted to explore the full potential of the proposed approach. In particular, we will integrate the proposed procedure with algorithms able to perform branch-switching and compute the bifurcation points of codimension-one.