Is large-scale vaccination sufficient for controlling the COVID-19 pandemic with uncertainties? A model-based study

Abstract

A massive vaccination programme against COVID-19 infection started at the beginning of 2021. Studies show that vaccinated people are subject to reinfection, and there is uncertainty in the rate of immunity loss, the force of infection, recovery rate and vaccine efficacy. Here we study a six-dimensional stochastic epidemic model with vaccine-induced immunity loss to demonstrate the effect of vaccination in controlling the COVID-19 epidemic. It is shown that the disease persists for a long time if the stochastic basic reproduction number $R^S_{0V}>1$ holds. We have also proved a sufficient condition for disease eradication. Our analysis shows that the disease cannot persist if $R_{0V}^{\text {ext}}<1$. However, this latter condition may not hold if the infectivity increases and/or the vaccine-induced immunity loss increases. Indian and Italian COVID-19 data are used to demonstrate various dynamical behaviours of the system and disease persistence. A non-trivial observation is that mass vaccination cannot eradicate the disease if the vaccine-induced immunity loss is high. Disease eradication is also challenging with the ongoing immunization process if the infectivity of the virus is also high. These results decipher that the infection will last long unless a long-lasting vaccine candidate appears or a low infectious variant replaces the highly contagious COVID-19 variant.

Appendices

Appendices

Appendix 1

Since the coefficients of the model system (1) are locally Lipschitz continuous, for any $\bigg (S(0),E(0),A(0),I(0),R(0),$ $V(0)\bigg )\in {\mathbb {R}}^6_+$, there is a unique local solution $\bigg (S(t),E(t),$ $A(t),I(t),R(t),V(t)\bigg )$ $\in {\mathbb {R}}^6_+$ for all $t\in [0,\tau _e)$, where $\tau _e$ is the explosion time [23]. We now prove $\tau _e=\infty$ a.s. so that the solution becomes global. Let $\kappa _0>0$ be sufficiently large for every coordinate $\bigg (S(0),E(0),A(0),I(0),$ $R(0),V(0)\bigg )$ lying within the interval $\left[ \frac{1}{\kappa _0},\kappa _0\right]$. We then define, for every integer $\kappa >\kappa _0$, the stopping time

$$\begin{aligned} \tau _\kappa&=\inf \bigg \{t{\in }[0,\tau _e):S(t){\notin }\left( \frac{1}{\kappa },\kappa \right) ,~E(t)\notin \left( \frac{1}{\kappa },\kappa \right) , \nonumber \\&~A(t)\notin \left( \frac{1}{\kappa },\kappa \right) ,~I(t)\notin \left( \frac{1}{\kappa },\kappa \right) , ~R(t)\notin \left( \frac{1}{\kappa },\kappa \right) , \nonumber \\&~V(t)\notin \left( \frac{1}{\kappa },\kappa \right) \bigg \}. \end{aligned}$$

(17)

Thus, $\tau _\kappa$ is increasing as $\kappa \rightarrow \infty$. Set $\lim _{\kappa \rightarrow \infty }\tau _\kappa =\tau _\infty$, when $\tau _\infty \le \tau _e$ a.s. We now show that $\tau _\infty =\infty$ by a contradiction. Let us assume that our claim is not true and there exist two constants $T_2>0$ and $\epsilon \in (0,1)$ such that $P(\tau _\infty \le T_2)>\epsilon .$ Thus, there exists an integer $\kappa _1\ge \kappa _0$ such that

$$\begin{aligned} P(\tau _\kappa \le T_2)\ge \epsilon ,~~\forall ~\kappa \ge \kappa _1. \end{aligned}$$

(18)

Noticing that $u+1-\ln {u}>0$ for all $u>0$ and $(S(t),E(t),A(t),I(t),R(t),V(t))\in {\mathbb {R}}^6_+$, we define the following positive definite function

$$\begin{aligned} \begin{aligned}&L=(S+1-\ln {S})+(E+1-\ln {E})+(A+1-\ln {A})\\&\quad +(I+1-\ln {I})+(R+1-\ln {R})+(V+1-\ln {V}). \end{aligned} \end{aligned}$$

Applying Ito’s formula, one can have

$$\begin{aligned} \text {d}L{} & {} =\left( 1-\frac{1}{S}\right) \text {d}S+\frac{1}{2S^2}(\text {d}S)^2+\left( 1-\frac{1}{E}\right) \text {d}E\\{} & {} \quad +\frac{1}{2E^2}(\text {d}E)^2 +\left( 1-\frac{1}{A}\right) \text {d}A+\frac{1}{2A^2}(\text {d}A)^2 \\{} & {} \quad +\left( 1-\frac{1}{I}\right) \text {d}I+\frac{1}{2I^2}(\text {d}I)^2+ \left( 1-\frac{1}{R}\right) \text {d}R\\{} & {} \quad +\frac{1}{2R^2}(\text {d}R)^2+ \left( 1-\frac{1}{V}\right) \text {d}V+\frac{1}{2V^2}(\text {d}V)^2\\{} & {} =\left( 1-\frac{1}{S}\right) \bigg [\bigg (\varLambda -qS-\frac{\beta S}{N}\left( (1-\kappa )I+\kappa A\right) -mS\\{} & {} \quad +gR\bigg )\text {d}t-\frac{\sigma _1 S}{N}((1-\kappa )I+\kappa A)~ \text {d}B_1(t)\bigg ]\\{} & {} \quad +\frac{1}{2N^2}\sigma _1^2((1-\kappa )I+\kappa A)^2 \text {d}t\\{} & {} \quad +\left( 1-\frac{1}{E}\right) \bigg [\bigg (\frac{\beta S}{N}\left( (1-\kappa )I+\kappa A\right) \\{} & {} \quad +\frac{\eta V}{N}\left( (1-\kappa )I+\kappa A\right) -(\omega +m)E\bigg )\text {d}t\\{} & {} \quad +\frac{\left[ (1-\kappa )I+\kappa A\right] }{N} (\sigma _1 S \text {d}B_1(t)+ \sigma _2 V \text {d}B_2(t))\bigg ]\\{} & {} \quad +\frac{1}{2N^2E^2}(\sigma _1^2 S^2 + \sigma _2^2 V^2)((1-\kappa )I+\kappa A)^2 \text {d}t\\{} & {} \quad +\left( 1-\frac{1}{A}\right) \big [\big (\delta \omega E -(\gamma _1+ \nu +m)A\big )\text {d}t\\{} & {} \quad -\sigma _3 A \text {d}B_3(t)\big ]+\frac{1}{2}\sigma _3^2 \text {d}t+\left( 1-\frac{1}{I}\right) \big [\big ((1-\delta ) \omega E\\{} & {} \quad -(\gamma +m+d_i)I+\nu A\big )\text {d}t-\sigma _4 I \text {d}B_4(t)\big ]+\frac{1}{2}\sigma _4^2 \text {d}t \\{} & {} \quad +\left( 1-\frac{1}{R}\right) \big [\left( \gamma _1 A+\gamma I-gR-mR \right) \text {d}t +\sigma _3A\text {d}B_3(t)\\{} & {} \quad +\sigma _4 I \text {d}B_4(t)\big ] +\frac{1}{2R^2}(\sigma _3 A \text {d}B_3(t)+ \sigma _4 I \text {d}B_4(t))^2\\{} & {} \quad +\left( 1-\frac{1}{V}\right) \bigg [\left( qS-\frac{\eta V}{N}\left[ (1-\kappa )I+\kappa A\right] -mV\right) \text {d}t\\{} & {} \quad -\frac{\sigma _2 V}{N}\left[ (1-\kappa )I+\kappa A\right] \text {d}B_2(t)\bigg ]\\{} & {} \quad + \frac{ \sigma _2^2}{2N^2} [(1-\kappa )I+\kappa A]^2 \text {d}t. \end{aligned}$$

Noting $u\le 2(u+1-\ln {u})$ for all $u>0$ and N is the total population, the above expression becomes

$$\begin{aligned} \begin{aligned} \text {d}L&\le \bigg [\varLambda +6m+q+\beta +\nu +d_i+g+ \omega +\gamma _1+\gamma +d_i\\&+\eta +\frac{1}{2}(\sigma _3^2+\sigma _4^2)\left( 1+\left( \frac{\varLambda }{m}\right) ^2\right) +2(S+1-\ln {S})\\&+2 \omega (E+1-\ln {E})+2 \gamma _1 (A+1-\ln {A})+\sigma _1^2+\sigma _2^2\\&+ 2 \gamma (I+1-\ln {I})\bigg ]dt+2 (R+1-\ln {R})\\&+2 (V+1-\ln {V})+ \frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A\\&+(1-\kappa )I] \text {d}B_1(t) +\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A\\&+(1-\kappa )I] \text {d}B_2(t) + \sigma _3 \left\{ 1-\frac{A}{R}\right\} \text {d}B_3(t) \\&+ \sigma _4 \left\{ 1-\frac{I}{R}\right\} \text {d}B_4(t). \end{aligned} \end{aligned}$$

Let $\varDelta _1=\varLambda +6\,m+q+\beta +\nu +d_i+g+ \omega +\gamma _1+\gamma +d_i+\eta +\frac{1}{2}(\sigma _3^2+\sigma _4^2)\left( 1+\left( \frac{\varLambda }{m}\right) ^2\right) +\sigma _1^2+\sigma _2^2$ and $\varDelta _2=\max \left\{ 1, \omega ,\gamma ,\gamma _1\right\}$. Then

$$\begin{aligned} \begin{aligned} dL&\le (\varDelta _1+\varDelta _2 L)\text {d}t+ \frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} \\&\quad [\kappa A+(1-\kappa )I] \text {d}B_1(t)\\&\quad +\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I] \text {d}B_2(t)\\&\quad + \sigma _3 \left\{ 1-\frac{A}{R}\right\} \text {d}B_3(t)+ \sigma _4 \left\{ 1-\frac{I}{R}\right\} \text {d}B_4(t). \end{aligned} \end{aligned}$$

Defining $\varDelta _3=\max \{\varDelta _1,\varDelta _2\}$, we have

$$\begin{aligned} \begin{aligned} \text {d}L&\le \varDelta _3(1+L)\text {d}t+ \frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} \\&\quad [\kappa A+(1-\kappa )I] \text {d}B_1(t) \\&\quad +\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I] \text {d}B_2(t)\\&\quad + \sigma _3 \left\{ 1-\frac{A}{R}\right\} \text {d}B_3(t)+ \sigma _4 \left\{ 1-\frac{I}{R}\right\} \text {d}B_4(t). \end{aligned} \end{aligned}$$

(19)

Noticing that

$$\begin{aligned} \begin{aligned}&\frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A+(1-\kappa )I] \le \sigma _1\left( 1-\frac{m}{\varLambda }\right) ,\\&\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I]\le \sigma _2\left( 1-\frac{m}{\varLambda }\right) ,\\&\sigma _3 \left\{ 1-\frac{A}{R}\right\} \le \sigma _3 \left( 1-\frac{m}{\varLambda }\right) ,\\&\sigma _4 \left\{ 1-\frac{I}{R}\right\} \le \sigma _4 \left( 1-\frac{m}{\varLambda }\right) , \end{aligned} \end{aligned}$$

we have

$$\begin{aligned}&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2}\Big | \frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A+(1-\kappa )I]\Big |^2 \text {d}t< \infty , \\&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \Big |\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I]\Big | ^2\text {d}t< \infty , \\&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \Big | \sigma _3 \left\{ 1-\frac{A}{R}\right\} \Big |^2 \text {d}t< \infty , \\&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \Big |\sigma _4 \left\{ 1-\frac{I}{R}\right\} \Big |^2 \text {d}t < \infty . \end{aligned}$$

Since all the functions $\frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A+(1-\kappa )I],$ $\frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I], \sigma _3 \left\{ 1-\frac{A}{R}\right\} ,\sigma _4 \left\{ 1-\frac{I}{R}\right\}$ are continuous, bounded and non-anticipative, then for a sequence of partition of the interval $[0,\tau _{\kappa _1} \wedge T_2 ]$ with mesh size $\varDelta t \rightarrow 0$, one have

$$\begin{aligned} \begin{aligned}&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2}\frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A+(1-\kappa )I]\text {d}B_1(t)\\&\quad = \lim _{\varDelta t \rightarrow 0} \varSigma _{j} {\mathbb {E}} \frac{\sigma _1}{N(t_j)}\left\{ 1-\frac{S(t_j)}{E(t_j)}\right\} \\&\qquad [\kappa A(t_j)+(1-\kappa )I(t_j)] \\&\qquad \times {\mathbb {E}} (B_1(t_{j+1})-B_1(t_j)) \\&\bigg [\because ~~ \frac{\sigma _1}{N(t_j)}\left\{ 1-\frac{S(t_j)}{E(t_j)}\right\} [\kappa A(t_j)+(1-\kappa )I(t_j)] ~\text{ and }\\ {}&~B_1(t_{j+1})-B_1(t_j) ~\text{ are } \text{ independent }\bigg ]. \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned}{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I] \text {d}B_2(t) \\{} & {} \quad = \lim _{\varDelta t \rightarrow 0} \varSigma _{j} {\mathbb {E}} \frac{\sigma _2}{N(t_j)}\left\{ 1-\frac{V(t_j)}{E(t_j)}\right\} \\{} & {} \qquad [\kappa A(t_j)+(1-\kappa )I(t_j)] \\{} & {} \qquad \times {\mathbb {E}} (B_2(t_{j+1})-B_2(t_j)), \\{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \sigma _3 \left( 1-\frac{A}{R}\right) \text {d}B_3(t)\\{} & {} \quad =\lim _{\varDelta t \rightarrow 0} \varSigma _{j} {\mathbb {E}} \left( \sigma _3 \left( 1-\frac{A(t_j)}{R(t_j)}\right) \right) {\mathbb {E}} (B_3(t_{j+1})-B_3(t_j)), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&{\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \sigma _4 \left( 1-\frac{I}{R}\right) \text {d}B_4(t)\\&\quad =\lim _{\varDelta t \rightarrow 0} \varSigma _{j} {\mathbb {E}} \left( \sigma _4 \left( 1-\frac{I(t_j)}{R(t_j)}\right) \right) {\mathbb {E}} (B_4(t_{j+1})-B_4(t_j)). \end{aligned} \end{aligned}$$

Using the fact that the increment of the Brownian motion is normally distributed with mean zero and variance ($t_{j+1}-t_j$), we have

$$\begin{aligned}{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2}\frac{\sigma _1}{N}\left\{ 1-\frac{S}{E}\right\} [\kappa A+(1-\kappa )I]\text {d}B_1(t)=0,\\{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \frac{\sigma _2}{N}\left\{ 1-\frac{V}{E}\right\} [\kappa A+(1-\kappa )I] \text {d}B_2(t) =0,\\{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \sigma _3 \left( 1-\frac{A}{R}\right) \text {d}B_3(t) =0, \\{} & {} {\mathbb {E}} \int _0^{\tau _{\kappa _1} \wedge T_2} \sigma _4 \left( 1-\frac{I}{R}\right) \text {d}B_4(t) =0. \end{aligned}$$

Integrating both sides of (19) from 0 to $\tau _{\kappa _1} \wedge T_2$, taking the expectation and using the above fact, we obtain

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}L \Big (S(\tau _{\kappa _1} \wedge T_2),E(\tau _{\kappa _1} \wedge T_2),A(\tau _{\kappa _1} \wedge T_2),I(\tau _{\kappa _1} \wedge T_2),\\&\qquad R(\tau _{\kappa _1} \wedge T_2), V(\tau _{\kappa _1} \wedge T_2)\Big ) \\&\quad \le L \Big (S(0),E(0), A(0), I(0), R(0), V(0)\Big )\\&\qquad +\varDelta _3~{\mathbb {E}}\int ^{\tau _{\kappa _1} \wedge T_2}_0(1+L)\text {d}t \\&\quad \le L\Big (S(0),E(0), A(0), I(0), R(0), V(0)\Big )+\varDelta _3 T_2\\&\qquad +\varDelta _3~E\int ^{\tau _\kappa \wedge T_2}_0 L\text {d}t. \end{aligned} \end{aligned}$$

Since L is an increasing function on $[0, \tau _{\kappa _1} \wedge T_2]$, for any $t \in [0,\tau _{\kappa _1} \wedge T_2],$ $L\bigg (S(t), E(t), A(t), I(t), R(t), V(t)\bigg )$ $\le L\bigg (S(\tau _{\kappa _1} \wedge T_2),$ $E(\tau _{\kappa _1} \wedge T_2), A(\tau _{\kappa _1} \wedge T_2), I(\tau _{\kappa _1} \wedge T_2),$ $R(\tau _{\kappa _1} \wedge T_2), V(\tau _{\kappa _1} \wedge T_2)\bigg ).$

$$\begin{aligned}&\therefore {\mathbb {E}}L \Big (S(\tau _{\kappa _1} \wedge T_2),E(\tau _{\kappa _1} \wedge T_2), A(\tau _{\kappa _1} \wedge T_2), I(\tau _{\kappa _1} \wedge T_2),\\&\quad R(\tau _{\kappa _1} \wedge T_2), V(\tau _{\kappa _1} \wedge T_2)\Big ) \\&\quad \le L\Big (S(0),E(0), A(0), I(0), R(0), V(0)\Big )+\varDelta _3 T_2 + \varDelta _3 \\&\qquad \times {\mathbb {E}}\int ^{\tau _{\kappa _1} \wedge T_2}_0 L\bigg (S(\tau _{\kappa _1} \wedge T_2),E(\tau _{\kappa _1} \wedge T_2), A(\tau _{\kappa _1} \wedge T_2),\\&\qquad I(\tau _{\kappa _1} \wedge T_2), R(\tau _{\kappa _1} \wedge T_2),V(\tau _{\kappa _1} \wedge T_2) \bigg )~\text {d}t \\&\quad \le L\Big (S(0),E(0), A(0), I(0), R(0), V(0)\Big )+\varDelta _3 T_2 + \varDelta _3 \\&\qquad \times \int ^{\tau _{\kappa _1} \wedge T_2}_0 {\mathbb {E}}L\bigg (S(\tau _{\kappa _1} \wedge T_2),E(\tau _{\kappa _1} \wedge T_2), A(\tau _{\kappa _1} \wedge T_2),\\&\qquad I(\tau _{\kappa _1} \wedge T_2), R(\tau _{\kappa _1} \wedge T_2),V(\tau _{\kappa _1} \wedge T_2)\bigg )~\text {d}t. \end{aligned}$$

Gronwall’s inequality then gives

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}L(S(\tau _{\kappa _1} \wedge T_2),E(\tau _{\kappa _1} \!\wedge \!T_2), A(\tau _{\kappa _1} \!\wedge \!T_2), I(\tau _{\kappa _1} \!\wedge \!T_2),\\&R(\tau _{\kappa _1} \wedge T_2),V(\tau _{\kappa _1} \wedge T_2)) \\&\quad \le (L(S(0),E(0), A(0), I(0), R(0), V(0))\\&\qquad +\varDelta _3T_2)e^{\varDelta _3(\tau _{\kappa _1} \wedge T_2)} =\varDelta _4 ~\text{(say) }. \end{aligned} \end{aligned}$$

(20)

Set $\varOmega _{\kappa _1}=\{\tau _{\kappa _1}\le T_2\}$ for all $\kappa _1\ge \kappa _2$. Thus, following (18), we get $P(\varOmega _{\kappa _1})\ge \epsilon _3$ for all $\omega _2\in \varOmega _{\kappa _1}$. Clearly, at least one of $S(\tau _{\kappa _1},\omega _2), ~E(\tau _{\kappa _1},\omega _2), ~A(\tau _{\kappa _1},\omega _2) ~I(\tau _{\kappa _1},\omega _2),$ $~R(\tau _{\kappa _1},\omega _2), ~V(\tau _{\kappa _1},\omega _2)$ is equal to either $\kappa _1$ or $\frac{1}{\kappa _1}$. Hence, $L(S(\tau _{\kappa _1}),E(\tau _{\kappa _1}),A(\tau _{\kappa _1}),I(\tau _{\kappa _1}),R(\tau {\kappa _1}),V(\tau {\kappa _1}))$ is no less than $\min \{\kappa _1+1-\ln {\kappa _1}, ~\frac{1}{\kappa _1}+1+\ln {\kappa _1}\}$. From (18) and (20), we then obtain

$$\begin{aligned} \begin{aligned} \varDelta _4&\ge {\mathbb {E}}[1_{\varOmega _{\kappa _1}}L(S(\tau _{\kappa _1},\omega _2),E(\tau _{\kappa _1},\omega _2),A(\tau _{\kappa _1},\omega _2),\\&\quad I(\tau _{\kappa _1},\omega _2),R(\tau _{\kappa _1},\omega _2),V(\tau _{\kappa _1},\omega _2))]\\&\ge \epsilon _3\left[ \left( \kappa _1+1-\ln {\kappa _1}\right) \wedge \left( \frac{1}{\kappa _1}+1+\ln {\kappa _1}\right) \right] , \end{aligned} \end{aligned}$$

where $1_{\varOmega _{\kappa _1}}$ is the indicator function of $\varOmega _{\kappa _1}$. Letting $\kappa _1\rightarrow \infty$, we get $\infty >\varDelta _4=\infty$, a contradiction. Hence, $\tau _\infty =\infty$ a.s. Hence, the theorem is proved.

Appendix 2

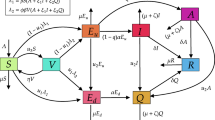
One can easily write the deterministic version of the stochastic model (1) as

$$\begin{aligned}&\frac{\text {d}S}{\text {d}t}=\varLambda -qS-\frac{\beta S}{N}\left[ (1-\kappa )I+\kappa A\right] -mS+gR,\nonumber \\&\frac{\text {d}E}{\text {d}t}=\frac{\beta S}{N}\left[ (1-\kappa )I+\kappa A\right] +\frac{\eta V}{N}\left[ (1-\kappa )I+\kappa A\right] \nonumber \\&~~~~~~~- \omega E-mE,\nonumber \\&\frac{\text {d}A}{\text {d}t}=\delta \omega E-(\gamma _1+\nu +m)A,\nonumber \\&\frac{\text {d}I}{\text {d}t}=(1-\delta )\omega E+\nu A-(\gamma +m+d_i)I,\nonumber \\&\frac{\text {d}R}{\text {d}t}=\gamma _1A+\gamma I-gR-mR,\nonumber \\&\frac{\text {d}V}{\text {d}t}=qS-\frac{\eta V}{N}\left[ (1-\kappa )I+\kappa A\right] -mV. \end{aligned}$$

(21)

Using the next-generation matrix method [9], the infection sub-system of the system (21), which describes the production of new infections and makes change in the states, reads

$$\begin{aligned} \begin{aligned}&\frac{\text {d}E}{\text {d}t}= \frac{\beta S}{N}\left[ (1-\kappa )I+\kappa A\right] +\frac{\eta V}{N}\left[ (1-\kappa )I+\kappa A\right] \\&~~~~~~~-(\omega +m)E, \\&\frac{\text {d}A}{\text {d}t}= \delta \omega E -\nu A-(\gamma _1+m)A, \\&\frac{\text {d}I}{\text {d}t}= (1-\delta )\omega E+\nu A-(\gamma +m+d_i)I. \end{aligned} \end{aligned}$$

(22)

The transmission matrix (F) and the transition matrix ($\varSigma$) associated with the system (22) are given by

$$\begin{aligned} {F}= & {} \left( \begin{array}{ccc} 0 &{} \kappa \frac{(\beta m+\eta q)}{q+m} &{} (1-\kappa )\frac{(\beta m+\eta q)}{q+m} \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} \right) \nonumber \\ { \varSigma }= & {} \left( \begin{array}{ccc} -(\omega +m) &{} 0 &{} 0 \\ \delta \omega &{} -(\nu +\gamma _1+m) &{} 0 \\ (1-\delta )\omega &{} \nu &{} -(\gamma +m+d_i) \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(23)

Then the deterministic basic reproduction number (DBRN) $R_{0V}^D$ of (21) is the spectral radius of the next-generation matrix $-{ F\varSigma ^{-1}}$, i.e. $R_{0V}^D=\rho (-{ F\varSigma ^{-1}})$, where ${ \varSigma ^{-1}}=$

$$\begin{aligned} \left( \begin{array}{ccc} -\frac{1}{\omega +m} &{} 0 &{} ~~0 \\ -\frac{\delta \omega }{(\omega +m)(\nu +\gamma _1+m)} &{} -\frac{1}{\nu +\gamma _1+m} &{} ~~0 \\ -\frac{\delta \omega \nu +(\nu +\gamma _1+m)(1-\delta )\omega }{(\omega +m)(\nu +\gamma _1+m)(\gamma +m+d_i)} &{} -\frac{\nu }{(\nu +\gamma _1+m)} \times &{} ~~-\frac{1}{\gamma +m+d_i} \\ &{} ~~~~\frac{1}{(\gamma +m+d_i)} &{} \\ \end{array} \right) . \end{aligned}$$

Thus, $R_{0V}^D$=$\frac{ \omega (\beta m+\eta q)\{\kappa \delta (\gamma +m+d_i)+(1-\kappa )\delta \nu +(1-\kappa )(1-\delta )(\nu +\gamma _1+m)\}}{(q+m)(\gamma +m+d_i)(\nu +\gamma _1+m)(\omega +m)}.$

If $R_{0V}^D>1$, then the disease is established in the system.

Fig. 7

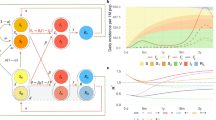
COVID-19 data fitting with the parameter values and noise intensities as in the Table 2. The first row provides the cumulative actual COVID-19 data (red-coloured curve) of the confirmed, recovered and vaccinated cases in Italy for the period 11 October 2021 to 18 January 2022. The solution (blue-coloured curve) of the stochastic model (1) is the fitted curve with the parameter values of the first row of Table 2. The other rows represent the same with the consecutive periods mentioned in Table 2

Appendix 3

Parameter estimation has been done in two steps [20]. First, we fitted the COVID-19 data with the corresponding deterministic system (21) and next the optimal noise intensities are determined to find the best-fitted parameter set for the stochastic system (1). In order to find the best-fitted parameter values of the deterministic system, we used a MATLAB embedded function, lsqcurvefit, which is a nonlinear solver that minimizes the sum of squared difference between the model output and a given data set. Here, a curve $h=g(x, \omega )$, parameterized by $\omega =(\omega _1, \omega _2,..., \omega _m)$, is fitted with the data points $(x_1,h_1), (x_2, h_2),...(x_m, h_m)$. The nonlinear least-squares method finds the certain value of the parameters such that $\varSigma _{i=1}^m \left( g(x_i, \omega )-h_i\right) ^2$ becomes minimum. With this best-fitted parameter set, we then find the optimum noise intensity for the stochastic system (1). Assuming 10,000 random values of $\sigma _1, \sigma _2, \sigma _3$ and $\sigma _4$ between 0 and 1, the stochastic system (2) is simulated 1000 times for each of these four tuples $(\sigma _1, \sigma _2, \sigma _3, \sigma _4)$. We then take the mean of those 1000 evolutions to determine the corresponding r-squared value. The particular value of $\sigma _1, \sigma _2, \sigma _3$ and $\sigma _4$ for which the r-squared value is closest to 1 is our required noise intensity.

Appendix 4