1 Introduction

Over the past years, a vast number of papers have been published on (2+1)-dimensional and (3+1)-dimensional nonlinear wave equations of the Korteweg-de Vries type, see, e.g., [1,2,3,4,5,6,7,8] and many other. All of these equations are integrable. The authors present many interesting analytical solutions: solitons, multi-solitons, breathers, lumps, etc., often using complex variables. The (2+1)-dimensional and (3+1)-dimensional equations used in these kinds of studies were not derived from fundamental laws of hydrodynamics but rather constructed by analogy to one-dimensional KdV-type equations. These constructions utilized integrability, symmetries and conservation laws, see, e.g., [9,10,11,12,13,14,15]. We deliberately do not discuss the works cited above in detail. This is because their significance is mainly mathematical, and the results of most of them are unlikely to be applicable to the description of real waves on the surface of shallow waters. Most of the extensions to (2+1)-dimensional and (3+1)-dimensional nonlinear wave equations are based on the KdV equation in the mathematical form, \( \eta _{t}+6 \eta \eta _{x} +\eta _{xxx}=0\) (a). It is often forgotten that the KdV equation is not a law of nature but only a first-order (in small parameters) approximation to a set of the Euler equations (equations (6–9) in this paper), limited to (x, z) spatial dimensions. Then, from Eqs. (6–9), one obtains the KdV equation (in the fixed reference frame, scaled coordinates) as \( \eta _{t} +\eta _{x} +\frac{3}{2} \alpha \eta \eta _{x}+ \frac{1}{6} \beta \eta _{xxx} =0\) (b). This equation is valid only when the parameters \(\alpha \) and \(\beta \) are small. When \(\alpha =\beta \) one can use scaling transformation to a moving reference frame \({\hat{x}}=\sqrt{\frac{3}{2}}(x-t)\) and \({\hat{t}}=\frac{1}{4}\sqrt{\frac{3}{2}}\alpha t\), which transforms the form (b) of the KdV equation to the mathematical form (a) in \(({\hat{x}},{\hat{t}})\) coordinates. In the form (a), there is no trace of small parameters, so its validity is not controlled. Moreover, one should remember that among analytic solutions to the KdV equation, there exist unphysical ones. For instance, the soliton solution to the equation (b) is \(\eta (x,t)=A\, \text {sech}^{2}\left[ \sqrt{\frac{3\,\alpha }{4\,\beta }A} \,(x-(1+\frac{\alpha }{2}A)t)\right] \). From the mathematical point of view, the soliton amplitudeA can be arbitrarily large, as well as the velocity \(1+\frac{\alpha }{2}A\). This is unphysical since high waves break. Also, the definition of \(\alpha \) in (10) implies that the amplitude in scaled variables should be close to 1. When the KdV equation is used in its mathematical form (or this form is extended to (2+1) or (3+1) dimensions), there is no control over the validity of its solutions. The same applies to generalizations of mathematical forms of the KdV equation to more than one spatial dimension.

Therefore, we see the need to derive appropriate equations in (2+1)-dimensions, the applicability of which is controlled. The new (2+1)-dimensional extended KdV equation derived in this paper from the basic equations of hydrodynamics satisfies this requirement. Moreover, since the extended (2+1)-dimensional KdV equation is the second-order (in small parameters) approximation to the set of the Euler equations (Eqs. (6–9)), it should be a more exact approximation than the (2+1)-dimensional KdV equation in shallow water problem. So, for the propagation of waves in shallow water, only this equation has a chance of being a good approximation.

Another set of articles worth mentioning are the papers [16,17,18,19,20,21,22]. In these papers, the authors considered wave propagation in multi-dimensional microstructured granular materials, magma equations for molten rocks, travelling wave solutions of the van der Waals normal form for granular matter, and magnetohydrodynamic waves in turbulent plasma.

In the previous paper [23], we derived (2+1)-dimensional extensions of three famous nonlinear wave equations: the Korteweg-de Vries equation, the fifth-order KdV equation and the Gardner equation. Unlike the works mentioned above, the derivation is based on a model of an ideal fluid with appropriate boundary conditions. Restricting ourselves to the first order in perturbation calculus, we found such relations between small parameters with physical significance that allowed us to reduce the Boussinesq equations to single (2+1)-dimensional wave equations. For other relations between small parameters, the system of Boussinesq’s equations becomes virtually impossible to simplify (see details in [24]). Moreover, in [23], we presented several families of analytic solutions to (2+1)-dimensional extension of the Korteweg-de Vries equation. These solutions include soliton solutions in the form \(A\,\text {sech}^{2}(\xi )\), periodic solutions in the form \(A\,\text {cn}^{2}(\xi ,m)\) and superposition solutions in the form \(\frac{A}{2}\left[ \text {dn}^{2}(\xi ,m)\pm \sqrt{m}\,\text {cn}(\xi ,m)\text {dn}(\xi ,m)\right] \), analogous to the solutions of the Korteweg-de Vries equation.

In the present paper, we first extend the Boussinesq equations to second order in small parameters and then find compatibility conditions leading to a single (2+1)-dimensional, extended KdV equation (KdV2). It is a unique (2+1)-dimensional extension of the well-known extended KdV equation (KdV2) derived first by Marchant and Smyth in 1990 [26]. Since recently we proved that the KdV2 equation possesses soliton solutions [27,28,29], periodic solutions [28, 29] and superposition solutions [29,30,31], here we investigate a hypothesis that the (2+1)-dimensional, extended KdV equation may possess analogous families of solutions.

The paper is organized as follows. In Sect. 2, we remind the set of Euler equations for shallow water in case of an inviscid, incompressible fluid with an irrotational motion under a gravity field. In Sect. 3, we derive the (2+1)-dimensional KdV equation in first-order approximation and the (2+1)-dimensional, extended KdV equation in second-order approximation. Additionally, we point out that the (2+1)-dimensional KdV equation implies the Kadomtsev–Petviashvili equation. Section 4 is devoted to solutions to (2+1)-dimensional, extended KdV equation. We show that for the (2+1)-dimensional, extended KdV equation, there are families of soliton, periodic and superposition solutions analogous to the families of solutions to the (1+1)-dimensional KdV and extended KdV equations. In Sect. 5, we show that all the solutions obtained in this work, formally two-dimensional, nevertheless represent one-dimensional motion, despite the highly complicated non-local (2+1)-dimensional, extended KdV equation. The paper finishes with conclusions and suggestions for future research.

2 Basic equations

Consider the inviscid and incompressible fluid whose motion is irrotational in a container with a flat, impenetrable bottom. In dimensional variables, the set of hydrodynamical equations consists of the Laplace equation for the velocity potential \(\phi (x,y,z,t)\) and boundary conditions at the surface and at the bottom

$$\begin{aligned}&\phi _{xx} + \phi _{yy} + \phi _{zz}= 0, \quad \text{ in } \text{ the } \text{ volume }, \end{aligned}$$
(1)
$$\begin{aligned}&\phi _z - ( \eta _x \phi _x + \eta _y \phi _y + \eta _t) = 0, \quad \text{ at } \text{ the } \text{ surface }, \end{aligned}$$
(2)
$$\begin{aligned}&\phi _t + \frac{1}{2}(\phi _x^2+\phi _y^2+\phi _z^2) +g \eta = 0, \quad \text{ at } \text{ the } \text{ surface }, \end{aligned}$$
(3)
$$\begin{aligned}&\phi _z = 0, \quad \text{ at } \text{ the } \text{ bottom }. \end{aligned}$$
(4)

Here, \(\eta (x,y,t)\) denotes the surface profile function, and g is the gravitational acceleration. Since we aim to describe wave propagation over macroscopic water basins, surface tension effects are safely neglected. Indexes denote partial derivatives, i.e., \(\phi _{x}\equiv \frac{\partial \phi }{\partial x}, ~\phi _{zz}\equiv \frac{\partial ^2 \phi }{\partial z^2}\), and so on. Introducing scaling to non-dimensional variables allows us to perform perturbation calculus when some parameters are small. Take the following scaling (in general, the scaling can be different in x-, y- and z-directions)

$$\begin{aligned} {\tilde{x}}&=\frac{x}{L_{x}}, \quad {\tilde{y}}= \frac{y}{L_{y}},\quad {\tilde{z}}= \frac{z}{H}, \quad {\tilde{t}}= \frac{t}{\frac{L_{x}}{\sqrt{gH}}}, \quad {\tilde{\eta }} = \frac{\eta }{A},\nonumber \\&\quad {\tilde{\phi }}= \frac{\phi }{L A\sqrt{\frac{g}{H}}}. \end{aligned}$$
(5)

Here, A is the amplitude of surface distortions from equilibrium shape (flat surface), H is average fluid depth, \(L_{x}\) is the average wavelength (in x-direction), and \(L_{y}\) is a wavelength in y-direction. The set of equations (1)-(4) takes the following form in the scaled variables (here and thereafter, we omit the tilde signs)

$$\begin{aligned}&\beta \phi _{xx} + \gamma \phi _{yy} + \phi _{zz}= 0, \end{aligned}$$
(6)
$$\begin{aligned}&\eta _t +\alpha \left( \eta _x\phi _x+\frac{\gamma }{\beta } \eta _y\phi _y \right) -\frac{1}{\beta }\phi _z = 0, \nonumber \\&\text{ for } z =1+\alpha \eta , \end{aligned}$$
(7)
$$\begin{aligned}&\phi _t + \frac{1}{2}\alpha \left( \phi _x^2+\frac{\gamma }{\beta }\phi _y^2+\frac{1}{\beta }\phi _z^2\right) + \eta = 0, \nonumber \\&\text{ for } z =1+\alpha \eta , \end{aligned}$$
(8)
$$\begin{aligned}&\phi _z = 0, \quad \text{ for } z =0, \end{aligned}$$
(9)

where parameters \(\alpha ,\beta ,\gamma \) are defined as follows

$$\begin{aligned} \alpha = \frac{A}{H}, \quad \beta = \left( \frac{H}{L_{x}}\right) ^2, \quad \gamma = \left( \frac{H}{L_{y}}\right) ^2. \end{aligned}$$
(10)

The velocity potential is sought in the form of power series in the vertical coordinate

$$\begin{aligned} \phi (x,y,z,t)=\sum _{m=0}^\infty z^m\, \phi ^{(m)} (x,y,t), \end{aligned}$$
(11)

where  \(\phi ^{(m)} (x,y,t)\) are yet unknown functions. The Laplace Eq. (6) and the boundary condition at the bottom (9) determine \(\phi \) in the form which involves only one unknown function with the lowest m-index, \(f(x,y,t):=\phi ^{(0)} (x,y,t)\) and its space derivatives. Hence,

$$\begin{aligned} \phi (x,y,z,t)&=\sum _{m=0}^\infty \frac{(-1)^m}{(2m)!} z^{2m}\,\left( \beta \partial _{xx}+\gamma \partial _{yy}\right) ^m f(x,y,t)\nonumber \\&= f -\frac{1}{2} z^2 \left( \beta f_{2x}+\gamma f_{2y}\right) \nonumber \\&\quad +\frac{1}{24} z^4 \left( \beta ^2 f_{4x}+2\beta \gamma f_{2x2y}+\gamma ^2f_{4y}\right) \nonumber \\&\quad - \frac{1}{720} z^6 \left( \beta ^3 f_{6x}+3\beta ^2\gamma f_{4x2y}\right. \nonumber \\&\quad \left. +3\beta \gamma ^{2}f_{2x4y}+\gamma ^{3}f_{6y}\right) + \cdots \end{aligned}$$
(12)

Then inserting the velocity potential (12) into boundary conditions at the unknown surface (7)-(8), one obtains the set of partial differential Boussinesq’s equations for two unknown functions f(x, y, t) and \(\eta (x,y,t)\). When the bottom is flat (9), these Boussinesq’s equations can be expressed up to arbitrary order in small parameters. Usually, the higher-order terms are neglected in the next steps, and considerations are limited to the first- or second-order equations. However, the explicit form of the resulting Boussinesq equations depends on a particular ordering of small parameters. For (1+1)-dimensional case, that is when f and \(\eta \) depend only on x, t, such research was done by Burde and Sergyeyev [32]. They showed that the Boussinesq equations can be reduced to a single well-known nonlinear wave equation for the wave profile \(\eta (x,t)\). And so, when \(\alpha =O(\beta )\), the Korteweg-de Vries equation results in first-order approximation and the extended Korteweg-de Vries equation (KdV2) in second-order approximation. When \(\alpha =O(\beta ^{2})\), the fifth-order KdV equation is obtained, and when \(\beta =O(\alpha ^{2})\), the result is the Gardner equation, both obtained in second-order approximation. In [32], the authors also derived several kinds of higher-order equations since this approach works up to arbitrary order for the flat bottom in (1+1)-dimensions.

3 (2+1)-dimensional KdV and extended KdV equations

It seems that in (2+1)-dimensional case, the scaling of the horizontal coordinates x, y should be the same (or similar). Then, assume that \(\alpha , \beta , \gamma \) are small parameters of the same order. Retaining only terms up to the first order in small parameters, one obtains the following form of the Boussinesq equations resulting from (7)-(8) (see [24])

$$\begin{aligned} \eta _t \!+\! f_{xx}\!&+\!\frac{\gamma }{\beta }f_{yy} \!+\!\alpha \!\left( \!\left( \eta f_x\right) _x\!+\! \frac{\gamma }{\beta }\left( \eta f_y\right) _y \!\right) \!\nonumber \\&-\!\frac{1}{6} \beta \!\left( \!f_{4x}+2 \frac{\gamma }{\beta } f_{2x2y} \!+\!\left( \!\frac{\gamma }{\beta }\right) ^2\!\!f_{4y}\!\right) \! =0, \end{aligned}$$
(13)
$$\begin{aligned} \eta +f_{t}&+\frac{1}{2} \alpha \left( f_{x}^{2} +\frac{\gamma }{\beta } f_{y}^{2} \right) \nonumber \\&-\frac{1}{2}\,\beta \left( f_{xxt} +\frac{\gamma }{\beta } f_{yyt}\right) =0. \end{aligned}$$
(14)

The presence of the term \(\frac{\gamma }{\beta }f_{yy}\) in the zeroth-order expression of (13) makes it impossible to eliminate the f-function and obtain the wave equation for \(\eta \) [24]. Instead, one can eliminate \(\eta \) and derive a complicated wave equation for f (still first-order). It reads as

$$\begin{aligned} f_{xx}&+ \frac{\gamma }{\beta } f_{yy} -f_{tt} -\alpha \left[ f_t\left( f_{xx} + \frac{\gamma }{\beta } f_{yy} \right) \right. \nonumber \\&\left. + \left( f_x^2+\frac{\gamma }{\beta } f_y^2\!\right) _t\right] \nonumber \\&+ \beta \left[ \frac{1}{3} \left( f_{4x}+2\frac{\gamma }{\beta }f_{2x2y}+\left( \frac{\gamma }{\beta }\right) ^2 f_{4y}\right) \right] =0. \end{aligned}$$
(15)

If the solution f(x, y, t) to (15) is known, the equation (14) supplies the surface profile function

$$\begin{aligned} \eta (x,y,t)= & {} -\left[ f_{t} +\frac{1}{2} \alpha \left( f_{x}^{2} +\frac{\gamma }{\beta } f_{y}^{2} \right) \right. \\{} & {} -\left. \frac{1}{2}\,\beta \left( f_{xxt} +\frac{\gamma }{\beta } f_{yyt}\right) \right] . \end{aligned}$$

However, obtaining the analytic solution of the equation (15) seems very difficult or even unfeasible.

How can we modify the derivation to avoid the term \(\frac{\gamma }{\beta }f_{yy}\) in the zeroth-order part of the Boussinesq equation? It is possible when we assume that \(\gamma =O(\beta ^{2})\), which is in line with the heuristic derivation of the Kadomtsev–Petviashvili equation [25]. For easier recognition of the orders of different terms, let us denote \( ~\alpha = A\,\beta , ~\gamma = G\,\beta ^{2}\), where A, G are arbitrary but close to 1. This notation relates three parameters to a single one. In the final equations, we will return to the original parameters \(\alpha ,\beta ,\gamma \).

In [23], with the above assumptions that \(\alpha =O(\beta ), ~\gamma =O(\beta ^{2})\), and flat bottom, we derived (2+1)-dimensional KdV equation in the following form

$$\begin{aligned} \eta _{t} +\eta _{x} +\frac{3}{2} \alpha \eta \eta _{x}+ \frac{1}{6} \beta \eta _{xxx} + \frac{\gamma }{2 \beta } \int \eta _{yy}\, dx =0.\nonumber \\ \end{aligned}$$
(16)

This equation is valid up to first-order terms in a fixed reference frame. Since in the present paper, we aim to study the (2+1)-dimensional, extended KdV equation which is second-order in small parameters, we recall from [23] the initial steps.

The Boussinesq equations obtained from (7)-(8), retaining terms up to second-order, are the following

$$\begin{aligned} \eta _{t}&+f_{xx} +\beta \left( A (f_{x} \eta )_{x} +G f_{yy}-\frac{1}{6} f_{4x}\right) + \beta ^2 \nonumber \\&\quad \left( A G (f_{y} \eta )_{y} -\frac{1}{2} A (f_{3x} \eta )_{x} -\frac{1}{3} G f_{xxyy}+\frac{1}{120} f_{6x}\right) \nonumber \\&=0, \end{aligned}$$
(17)
$$\begin{aligned} \eta&+f_{t} +\beta \left( \frac{1}{2} A f_{x}^2-\frac{1}{2} f_{xxt}\right) \nonumber \\&+\beta ^2 \left( \frac{1}{2} A G f_{y}^2-A f_{xxt} \eta +\frac{1}{2} A f_{xx}^2\right. \nonumber \\&\left. -\frac{1}{2} A f_{x} f_{3x}-\frac{1}{2} G f_{yyt}+\frac{1}{24} f_{4xt}\right) =0. \end{aligned}$$
(18)

Now we take x-derivative of (18) and denote \(w\!:=\!f_{x}\) in both Boussinesq’s Eqs. (17–18). So, we have

$$\begin{aligned} \eta _{t} +w_{x}&+\beta \left( A (\eta w)_{x} +G \!\int \! w_{yy}\,dx-\frac{1}{6} w_{3x}\right) \end{aligned}$$
(19)
$$\begin{aligned}&+ \beta ^2 \left( A G (\eta \!\int \! w_{y}\,dx)_{y} -\frac{1}{2} A (\eta \, w_{2x})_{x}\right. \nonumber \\&\left. -\frac{1}{3} G w_{xyy}+\frac{1}{120}w_{5x}\right) =0, \nonumber \\ w_{t} +\eta _{x}&+\beta \left( A \,w w_{x} -\frac{1}{2} w_{xxt}\right) \nonumber \\&+ \beta ^2 \left( A G w_{y} \!\int \! w_{y}\,dx - A (\eta \, w_{xt})_{x} \right. \nonumber \\&\left. +\frac{1}{2} A \,w_{x} w_{xx} -\frac{1}{2} A \,w w_{xxx}\right. \nonumber \\&\left. -\frac{1}{2} G w_{yyt}+\frac{1}{24} w_{4xt}\right) =0. \end{aligned}$$
(20)

Then in zeroth-order the following holds

$$\begin{aligned}{} & {} \eta _{t}+w_{x}=0, \quad w_{t}+\eta _{x}=0 \quad \Longrightarrow \quad w=\eta ,\nonumber \\{} & {} \quad w_{t}=-w_{x}, \quad \eta _{t}=-\eta _{x}. \end{aligned}$$
(21)

Relations (21) are crucial in derivations of all one-dimensional KdV-type equations (KdV, fifth-order KdV, Gardner) from ideal fluid model since they allow for appropriate replacements of t-derivatives by x -derivatives.

To make compatible Boussinesq’e Eqs. (17–18) only up to first-order we postulate w in the form

$$\begin{aligned} w =\eta +w^{(1)} = \eta +\alpha Q^{(a)}+\beta Q^{(b)}+\frac{\gamma }{\beta } Q^{(g)}, \end{aligned}$$
(22)

where \(\alpha Q^{(a)}, \beta Q^{(a)}, \frac{\gamma }{\beta } Q^{(g)}\) are first-order corrections. Now, we insert w given by (22) into (17)-(18) and retain terms up to first order. The result from (17) is

$$\begin{aligned}{} & {} \eta _{x} + \eta _{t} +\alpha \left( Q^{(a)}_{x} +2 \eta \eta _{x}\right) +\beta \left( Q^{(b)}_{x} -\frac{1}{6} \eta _{xxx}\right) \nonumber \\{} & {} + \frac{\gamma }{\beta }\left( Q^{(g)}_{x} \!+\! \int \! \eta _{yy}\, dx\,\right) =0. \end{aligned}$$
(23)

From (18), we obtain

$$\begin{aligned}{} & {} \eta _{x} + \eta _{t} +\alpha \left( Q^{(a)}_{t} +\eta \eta _{x} \right) +\beta \left( Q^{(b)}_{t} -\frac{1}{2} \eta _{xxt}\right) \nonumber \\{} & {} +\frac{\gamma }{\beta }\left( Q^{(g)}_{t} \right) = 0. \end{aligned}$$
(24)

Subtracting (24) from (23) and replacing t-derivatives by \((-)x\)-derivatives (thanks to (21), \(Q^{(a)}_{t} \rightarrow -Q^{(a)}_{x}, Q^{(g)}_{t} \rightarrow -Q^{(g)}_{x}\), \(\eta _{xxt}\rightarrow - \eta _{xxx}\)) we receive

$$\begin{aligned}{} & {} \alpha (2 Q^{(a)}_{x} + \eta \eta _{x}) +\beta \left( 2 Q^{(b)}_{x} -\frac{2}{3} \eta _{xxx}\right) \nonumber \\{} & {} + \frac{\gamma }{\beta } \left( 2Q^{(g)}_{x}+\int \eta _{yy}\, dx\,\right) =0. \end{aligned}$$
(25)

Due to arbitrariness of small parameters, (25) is equivalent to three independent equations

$$\begin{aligned}{} & {} Q^{(a)}_{x} = -\frac{1}{2}\eta \eta _{x}, \qquad Q^{(b)}_{x} = \frac{1}{3} \eta _{xxx},\nonumber \\{} & {} \qquad Q^{(g)}_{x} = - \frac{1}{2}\int \eta _{yy}\, dx. \end{aligned}$$
(26)

Integration of equations (26) over x yields

$$\begin{aligned}{} & {} Q^{(a)} = -\frac{1}{4}\eta ^{2}, \qquad Q^{(b)} = \frac{1}{3} \eta _{xx}\nonumber \\{} & {} \qquad Q^{(g)} = - \frac{1}{2} \int \left( \int \eta _{yy}\, dx\right) dx. \end{aligned}$$
(27)

Indeed,

$$\begin{aligned}{} & {} w = \eta +\alpha \left( - \frac{1}{4} \eta ^{2}\right) +\beta \left( \frac{1}{3} \eta _{xx}\right) \nonumber \\{} & {} +\frac{\gamma }{\beta }\left( - \frac{1}{2}\int (\int \eta _{yy}\, dx )dx\right) \end{aligned}$$
(28)

reduces both Boussinesq’s equations to the same wave equation (16) when restricted to first-order terms.

To derive second-order wave equation, let us postulate w in the form

$$\begin{aligned} w=&\eta + \beta \left( -\frac{1}{4} A \eta ^2 +\frac{1}{3} u_{xx} -\frac{1}{2} \beta G \int (\int \eta _{yy}\,dx)\,dx \right) \nonumber \\&\quad +\beta ^{2} \left( \frac{1}{8} A^2 \eta ^3 +A \left( \frac{3}{16} \eta _{x}^2+\frac{1}{2} \eta \eta _{x}\right) \right. \nonumber \\&\quad \left. +\frac{1}{10} \eta _{4x} +A G\, \text {Q} + G^2 \text {P} + G\, \text {R} \right) , \end{aligned}$$
(29)

where \(\text {Q},\text {P},\text {R}\) are yet unknown second-order correction functions related to \(\frac{\alpha \gamma }{\beta }, \frac{\gamma ^{2}}{\beta ^{2}}, \gamma ^{2}\), respectively. Terms in the first row are known from the derivation of the first-order Eq. (16) in [23]. Terms \(\frac{1}{8} A^2 \eta ^3, A \Big (\frac{3}{16} \eta _{x}^2 +\frac{1}{2} \eta \eta _{x}\Big ), \frac{1}{10} \eta _{4x}\) are correction functions related to \(\alpha ^{2}, \alpha \beta , \beta ^{2}\), respectively, known from one-dimensional KdV2 equation (see, [27, 32]).

Substituting (29) into (19) and retaining terms up to second-order yields

$$\begin{aligned} \eta _{t}&+\eta _{x} + \beta \left( \frac{3}{2} A \eta \eta _{x}+\frac{1}{2} G \!\int \! \eta _{yy}\,dx+\frac{1}{6} \eta _{3x}\right) \nonumber \\&+ \beta ^2 \left( -\frac{3}{8} A^2 \eta ^2 \eta _{x}+A G\, \text {Q}_{x}\right. \nonumber \\&-\frac{1}{2} A G \!\int \! \eta _{y}^2\,dx -\frac{1}{2} A G \!\int \! \eta \eta _{yy}\,dx\nonumber \\&\left. +\frac{1}{2} A G\, \eta \!\int \!\eta _{yy} \,dx \right. \nonumber \\&+A G\, \eta _{y} \!\int \! \eta _{y}\,dx -\frac{1}{2} A G\, \eta _{x} (\!\int \! (\!\int \! \eta _{yy}\,dx)\,dx)\nonumber \\&+\frac{23}{24}A\, \eta _{x} \eta _{xx}+\frac{5}{12} A\, \eta \eta _{3x}\nonumber \\&\left. +G^2\, \text {P}_{x} -\frac{1}{2} G^2 \!\int \! (\!\int \! (\!\int \! \eta _{4y} \, dx)\,dx)\,dx +G\, \text {R}_{x}\right. \nonumber \\&\left. +\frac{1}{12} G\, \eta _{xyy}+\frac{19}{360} \eta _{5x}\right) =0, \end{aligned}$$
(30)

whereas substituting (29) into (20) and retaining terms up to second-order yields

$$\begin{aligned} \eta _{t}&+\eta _{x} + \beta \left( \frac{3}{2} A \eta \eta _{x}+\frac{1}{2} G \!\int \! \eta _{yy}\,dx+\frac{1}{6} \eta _{3x}\right) \nonumber \\&+ \beta ^2 \left( -\frac{3}{8} A^2 \eta ^2 \eta _{x}-A G\, \text {Q}_{x}+\frac{3}{4} A G \!\int \! \eta _{y}^2 \,dx\right. \nonumber \\&\left. +\frac{3}{4} A G \!\int \! \eta \eta _{yy}\,dx -\frac{1}{4} A G\, \eta \!\int \! \eta _{yy}\,dx \right. \nonumber \\&+A G\, \eta _{y} \!\int \! \eta _{y}\,dx -\frac{1}{2} A G\, \eta _{x} \!\int \! (\!\int \! \eta _{yy}\,dx)\,dx\nonumber \\&+\frac{23}{24} A\, \eta _{x} \eta _{xx}+\frac{5}{12} A\, \eta \eta _{3x} \nonumber \\&\left. -G^2\, \text {P}_{x} +\frac{1}{4} G^2\, \!\int \! (\!\int \! (\!\int \! \eta _{4y}\,dx)\,dx)\,dx\right. \nonumber \\&\left. -G\,\text {R}_{x}+\frac{5}{12} G\, \eta _{xyy}+\frac{19}{360} \eta _{5x}\right) =0. \end{aligned}$$
(31)

On the way to the result (31), the t-derivatives had to be converted into x-derivatives appropriately. In the first-order terms, it was necessary to use the solution of the first-order equation, i.e.,  \(\eta _{t}=-\bigg (\eta _{x} +\frac{3}{2} \eta \eta _{x} +\frac{1}{6}\eta _{3x} +\frac{\gamma }{2\beta }\int \eta _{yy}\,dx \bigg )\). In second-order terms, it is enough to use the zero-order relations, \(\eta _{t}=-\eta _{x}, \eta _{yyt}=-\eta _{xyy},\text {R}_{t}=-\text {R}_{x}\), and so on. It is worth recalling that all these relations follow from the fact that, under assumption \(\gamma \approx \beta ^2\), the zeroth-order terms in the Boussinesq Eqs. (17–18) do not contain y-derivatives.

Subtraction (31) from (30) gives

$$\begin{aligned} \beta ^{2}&\left( 2 A G\, \text {Q}_{x}-\frac{5}{4} A G \!\int \! \eta _{y}^2\,dx-\frac{5}{4} A G\, \!\int \! \eta \eta _{yy}\,dx\right. \nonumber \\&\left. +\frac{3}{4} A G\, \eta \!\int \! \eta _{yy}\,dx \right. \nonumber \\&\left. +2 G^2\, \text {P}_{x} -\frac{3}{4} G^2 \!\int \! (\!\int \! (\!\int \! \eta _{4y}\,dx)\,dx)\,dx\right. \nonumber \\&\left. +2 G \text {R}_{x}-\frac{1}{3} G\,\eta _{xyy} \right) =0. \end{aligned}$$
(32)

Because of the arbitrariness of small parameters, equation (32) is equivalent to three equations that should be fulfilled simultaneously

$$\begin{aligned} 2\,\text {Q}_{x}&-\frac{5}{4}\!\int \! \eta _{y}^2\,dx-\frac{5}{4} \!\int \! \eta \eta _{yy}\,dx+\frac{3}{4}\, \eta \!\int \! \eta _{yy}\,dx = 0. \end{aligned}$$
(33)
$$\begin{aligned} 2\,\text {R}_{x}&-\frac{1}{3}\, \eta _{xyy} =0, \qquad \text{ and } \nonumber \\ 2\, \text {P}_{x}&-\frac{3}{4} \!\int \! (\!\int \! (\!\int \! \eta _{4y}\,dx)\,dx)\,dx=0. \end{aligned}$$
(34)

Integrating the above equations, we obtain the correction functions

$$\begin{aligned} \text {Q}&= \frac{5}{8}\!\int \! (\eta _{y}^2+\eta \eta _{yy}) \,dx -\frac{3}{8}\!\int \! \left( \eta \!\int \! \eta _{yy}\,dx \right) \,dx, \end{aligned}$$
(35)
$$\begin{aligned} \text {R}&= \frac{1}{6}\, \eta _{yy}, \quad \text{ and } \nonumber \\ \text {P}&= \frac{3}{8} \int \left( \int \left( \int \left( \int \eta _{4y}\,dx \right) \,dx \right) \,dx \right) \,dx. \end{aligned}$$
(36)

So, finally with

$$\begin{aligned} w&= \eta + \beta \left( -\frac{1}{4} A \eta ^2 +\frac{1}{3} u_{xx} -\frac{1}{2} \beta G \int (\int \eta _{yy}\,dx)\,dx \right) \nonumber \\&\quad +\beta ^{2} \left( A^2 \frac{1}{8} \eta ^3 +A \left( \frac{3}{16} \eta _{x}^2+\frac{1}{2} \eta \eta _{x}\right) +\frac{1}{10} \eta _{4x} \right. \nonumber \\&\quad +A G\, \left( \frac{5}{8}\!\int \! (\eta _{y}^2+\eta \eta _{yy}) \,dx -\frac{3}{8}\!\int \! (\eta \!\int \! \eta _{yy}\,dx)\,dx \right) \nonumber \\&\left. \quad + G^2\, \frac{3}{8} \!\int \! \left( \!\int \! \left( \!\int \! \left( \!\int \! \eta _{4y}\,dx \right) \,dx \right) \,dx \right) \,dx + G\, \frac{1}{6}\, \eta _{yy} \right) , \end{aligned}$$
(37)

we obtained from the Boussinesq Eqs. (17–18) the same second-order shallow water equation valid up to second-order terms

$$\begin{aligned} \eta _{t}&+\eta _{x} + \frac{3}{2} \alpha \eta \eta _{x} +\frac{1}{6}\beta \eta _{3x} +\frac{1}{2} \frac{\gamma }{\beta } \!\int \! \eta _{yy}\,dx \nonumber \\&-\frac{3}{8} \alpha ^2 \eta ^2 \eta _{x} +\alpha \beta \left( \frac{23}{24}\, \eta _{x} \eta _{xx}+\frac{5}{12}\, \eta \eta _{3x}\right) \nonumber \\&+ \frac{19}{360}\beta ^2 \eta _{5x} +\frac{1}{4}\gamma \,\eta _{xyy} \nonumber \\&+ \frac{\alpha \gamma }{\beta } \left( \frac{3}{4} \!\int \! \eta _{y}^2\,dx +\frac{3}{4} \!\int \! \eta \eta _{yy}\,dx +\frac{5}{4}\, \eta \!\int \! \eta _{yy} \,dx\right. \nonumber \\&\left. -\frac{1}{2}\, \eta _{x} \!\int \! (\!\int \! \eta _{yy}\,dx)\,dx\right) \nonumber \\&-\frac{1}{8}\frac{\gamma ^{2}}{\beta ^{2}} \!\int \! \left( \!\int \! \left( \!\int \! \eta _{4y} \, dx \right) \,dx \right) \,dx =0. \end{aligned}$$
(38)

It is worth noting that for single space dimension (\(\frac{\partial \eta }{\partial y}=0\)), the equation (38) reduces to the well-known extended Korteweg-de Vries equation (KdV2) [26, 28, 30,31,32]

$$\begin{aligned} \eta _{t}&+\eta _{x} +\frac{3}{2} \alpha \eta \eta _{x} +\frac{1}{6}\beta \eta _{3x} -\frac{3}{8} \alpha ^2 \eta ^2 \eta _{x}\nonumber \\&+\alpha \beta \left( \frac{23}{24}\, \eta _{x} \eta _{xx}+\frac{5}{12}\, \eta \eta _{3x}\right) + \frac{19}{360}\beta ^2 \eta _{5x}= 0. \end{aligned}$$
(39)

Therefore, equation (38) deserves the name (2+1)-dimensional extended Korteweg-de Vries equation.

3.1 The Kadomtsev–Petviashvili equation

The (2+1)-dimensional KdV equation (16) implies the Kadomtsev–Petviashvili equation. Differentiating (16) over x yields

$$\begin{aligned}{} & {} \frac{\partial }{\partial x}\left( \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} +\frac{3}{2} \alpha \, u \frac{\partial u}{\partial x} +\frac{1}{6} \beta \, \frac{\partial ^{3} u}{\partial x^{3}} \right) =\nonumber \\{} & {} -\lambda \, \frac{\partial ^{2} u}{\partial y^{2}}, \quad \text{ where } \quad \lambda =\frac{1}{2} \frac{\gamma }{\beta }. \end{aligned}$$
(40)

Equation (40) can be named the Kadomtsev–Petviash vili equation in a fixed reference frame. It is derived in the first-order perturbation approach from the ideal fluid model when \(\alpha \approx \beta \) and \(\gamma \approx \beta ^{2}\).

The classical Kadomtsev–Petviashvili equation [25] has the following form

$$\begin{aligned} \frac{\partial }{\partial {\hat{x}}}\left( \frac{\partial u}{\partial {\hat{t}}} +6 u \frac{\partial u}{\partial {\hat{x}}} + \frac{\partial ^{3} u}{\partial {\hat{x}}^{3}} \right) = -\lambda \, \frac{\partial ^{2} u}{\partial {\hat{y}}^{2}}. \end{aligned}$$
(41)

Equation (41) with \(\lambda >0\) is called KP2 equation, whereas (41) with \(\lambda <0\) is called KP1.

Let us make a scaling transformation of (40) to a moving reference frame.

Take \( {\hat{x}} =\sqrt{\frac{3}{2}}(x-t)\), \( {\hat{t}} =\frac{1}{4} \sqrt{\frac{3}{2}}\,\alpha t,\) and \({\hat{y}}= y\).   Then  \(\frac{\partial ~}{\partial x}=\sqrt{\frac{3}{2}}\frac{\partial ~}{\partial {\hat{x}}}\),

\(\frac{\partial u}{\partial t}=\sqrt{\frac{3}{2}}(\frac{\alpha }{4}\frac{\partial u}{\partial {\hat{t}}}-\frac{\partial u}{\partial {\hat{x}}})\),  \(\frac{\partial u}{\partial x}=\sqrt{\frac{3}{2}}\frac{\partial u}{\partial {\hat{x}}}\), \(\frac{\partial ^{3} u}{\partial x^{3}}=\frac{3}{2}\sqrt{\frac{3}{2}}\frac{\partial ^{3} u}{\partial {\hat{x}}^{3}}\)  and  \(\frac{\partial ^{2} u}{\partial y^{2}}=\frac{\partial ^{2} u}{\partial {\hat{y}}^{2}}\).

So, in the moving reference frame, equation (40) receives the form

$$\begin{aligned} \frac{\partial }{\partial {\hat{x}}}\left( \frac{\partial u}{\partial {\hat{t}}} +6 u \frac{\partial u}{\partial {\hat{x}}} +\frac{\beta }{\alpha } \frac{\partial ^{3} u}{\partial {\hat{x}}^{3}} \right) = -\lambda \, \frac{\partial ^{2} u}{\partial {\hat{y}}^{2}} \end{aligned}$$
(42)

where \(\lambda =\frac{4}{3} \frac{\gamma }{\alpha \beta }\). In case \(\alpha =\beta \), equation (42) coincides with the classical Kadomtsev–Petviashvili equation (41). To our best knowledge, this is the first derivation of the KP equation from the ideal fluid model.

Differentiation (2+1)-dimensional, extended KdV equation (38) over x does not remove the high nonlocality of the resulting equation. So, an extended analogue to the KP equation (40) does not exist.

4 Search for solutions to (2+1)-dimensional extended KdV equation

In 2014, we showed that for the (1+1)-dimensional, extended KdV equation (39), there exist soliton solutions in the same form as those for the KdV equation, that is, \(\eta = A\, \text {sech}[B(x-vt)]^{2}\) [27]. Next, in 2018 [28, 30, 31], we showed that the periodic (cnoidal) and superposition solutions to the extended KdV equation have the same form as the corresponding solutions to the KdV equation, as well. It is, therefore, natural to look for solutions to (2+1)-dimensional, extended KdV equation (38) in a form analogous to the solutions to (2+1)-dimensional Korteweg-de Vries equation (16) that we discussed in [23].

Similarly, as in [23], let us look for solutions in the form

$$\begin{aligned}{} & {} \eta (x,y,t)=\eta (k x+l y- \omega t)\equiv \eta (\xi ),\nonumber \\{} & {} \quad \text{ where } \quad \xi =k x+l y- \omega t. \end{aligned}$$
(43)

For \(\eta \) in the form (43) equation (38) reduces to ODE form

$$\begin{aligned}&\left( k + \frac{\gamma }{2 \beta } \frac{l^{2}}{k}-\frac{\gamma ^{2}}{8 \beta ^{2}}\frac{l^{4}}{k^{3}} -\omega \right) \eta _{\xi } \nonumber \\&+ \left( \frac{\beta }{6} k^{3}+ \frac{\gamma }{4}k l^{2}\right) \eta _{3\xi } +\left( \frac{3\alpha }{2}k + \frac{3\alpha \gamma }{4\beta }\frac{l^{2}}{k}\right) \,\eta \eta _{\xi } \nonumber \\&-\frac{3\alpha ^{2}}{8} k\, \eta ^{2}\eta _{\xi } +\frac{23}{24}\alpha \beta \, k^{3} \eta _{\xi } \eta _{\xi \xi }+\frac{5}{12}\alpha \beta \, k^{3} \eta \eta _{3\xi }\nonumber \\&+\frac{19}{360} \beta ^{2}k^{5} \eta _{5\xi } \nonumber \\&+ \frac{3\alpha \gamma }{4\beta }\frac{l^{2}}{k}\!\int (\eta _{\xi }^{2}+\eta \eta _{\xi \xi } )\,d\xi =0. \end{aligned}$$
(44)

To simplify the notation denote (44) in the following form

$$\begin{aligned} \text {A1}\, \eta _{\xi }&+ \text {A2}\, \eta _{3\xi } + \text {A3}\,\eta \eta _{\xi } + \text {A4}\, \eta ^{2}\eta _{\xi } + \text {A5}\,\eta _{\xi } \eta _{\xi \xi }\nonumber \\&+\text {A6}\, \eta \eta _{3\xi } + \text {A7}\, \eta _{5\xi } + \text {A8}\! \!\int \!(\eta _{\xi }^{2}+\eta \eta _{\xi \xi } )d\xi {=}0. \end{aligned}$$
(45)

4.1 Soliton solutions

Suppose that the solution to the (2+1)-dimensional extended KdV equation (38) has the same form as the solution to (2+1)-dimensional KdV equation, that is,

$$\begin{aligned} \eta (x,y,t)=A\, \text {sech}^{2} (k x+l y-\omega t)=A\,\text {sech}^{2} (\xi ). \end{aligned}$$
(46)

Then inserting (46) into (45) yields

$$\begin{aligned} -\frac{1}{4} A&\bigg [ 8 A^2 \text {A4} -48 A \text {A5}-96 A \text {A6} +2880 \text {A7} \nonumber \\&+\cosh ^2(x) (8 A\text {A3}+32 A\text {A5}+32 A\text {A6} +8A\text {A8} \nonumber \\&-96 \text {A2}-1920\text {A7}) +\cosh ^4(x)\nonumber \\&(8 \text {A1}+32 \text {A2}+128 \text {A7}) \bigg ] \tanh (x) \text {sech}^6(x) =0. \end{aligned}$$
(47)

Equation (47) is satisfied when simultaneously

$$\begin{aligned}&8 A^2 \text {A4} -48 A \text {A5}-96 A \text {A6} +2880 \text {A7} = 0, \end{aligned}$$
(48)
$$\begin{aligned}&8 A\text {A3}+32 A\text {A5}+32 A\text {A6}+8 A\text {A8}-96 \text {A2}-1920 \text {A7} = 0, \end{aligned}$$
(49)
$$\begin{aligned}&\text{ and } \quad 8 \text {A1}+32 \text {A2}+128 \text {A7} = 0. \end{aligned}$$
(50)

Now, we replace \(\text {A1}-\text {A8}\) by their original values according to equation (44). Then we have

$$\begin{aligned}&-3 \alpha ^2 A^2 k-86 \alpha A \beta k^3+152 \beta ^2 k^5 =0, \end{aligned}$$
(51)
$$\begin{aligned}&44 \alpha A \beta k^3+12 \alpha A k+\frac{12 \alpha A \gamma l^2}{\beta k}-\frac{304}{3} \beta ^2 k^5-16 \beta k^3-24 \gamma k l^2 =0, \end{aligned}$$
(52)
$$\begin{aligned}&\frac{304 \beta ^2 k^5}{45}+\frac{16 \beta k^3}{3}-\frac{\gamma ^2 l^4}{\beta ^2 k^3}+\frac{4 \gamma l^2}{\beta k}+8 \gamma k l^2+8 k-8 \omega = 0 \end{aligned}$$
(53)

from (48), (49) and (50), respectively. Equation (51) has two roots

$$\begin{aligned}{} & {} A_{1}=\frac{\beta k^{2}}{3\alpha }(-43-\sqrt{2305}),\nonumber \\{} & {} \qquad A_{2}=\frac{\beta k^{2}}{3\alpha }(-43+\sqrt{2305}). \end{aligned}$$
(54)

The root \(A_{1}\), however, has to be rejected because it implies \(l^{2}<0\) from (52) (remember that \(\beta ,\gamma >0\) by their definitions). This property is analogous to that obtained by us for a one-dimensional extended KdV Eq. in [27]. There, we also obtained two roots for A. The negative one, \(A_{1}\) leads to imaginary D in argument of the solution \(\eta = A_{1} \text {sech}^{2}[B(x-vt)]\), so has to be rejected.

From (52), with \(A=A_{2}\), we have

$$\begin{aligned}{} & {} l^{2} = \frac{\beta k^2 \left[ 3 (\sqrt{2305}+1) -\beta k^2 ( 5 \sqrt{2305} +773)\right] }{144 \gamma } \,\nonumber \\{} & {} \approx \frac{\beta k^2}{\gamma } \left( 1.021-7.035 \beta k^2\right) . \end{aligned}$$
(55)

With this \(l^{2}\) Eq. (53) implies

$$\begin{aligned} \omega =&\frac{\left( 8159\!+\!95 \sqrt{2305}\right) }{9216} k \!+\!\frac{19 \left( 23 \sqrt{2305}\!-\!1129\right) }{13824}\beta k^3\nonumber \\&\!-\!\frac{19 \left( 184943\!+\!1775 \sqrt{2305}\right) }{414720}\beta ^2 k^5 \nonumber \\&\approx k\left( 1.38021 - 0.0340313\,\beta k^2 - 12.3772\,\beta ^2 k^4 \right) . \end{aligned}$$
(56)

So, it appears that the function (46), that is \(\eta =A\, \text {sech}(\xi )^{2}\), is the solution to (2+1)-dimensional extended KdV Eq. (38) with \(A_{2},l,\omega \) given by (54),(55) and (56), respectively.

Let us discuss allowable solutions. The condition \(l^{2}\ge 0\) implies

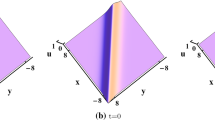
$$\begin{aligned}{} & {} 0<\beta k^{2}<\frac{3(1+\sqrt{2305})}{(773+5\sqrt{2305})} \approx 0.145137 \quad \Longrightarrow \nonumber \\{} & {} \quad (k^{2})_{\text {max}}\approx \frac{0.145137}{\beta }. \end{aligned}$$
(57)

Then the allowable solutions have k limited by the condition  \(k^{2}<(k^{2})_{\text {max}}\). Let us consider an example of a soliton solution. Take \(\alpha =0.15\),  \(\beta =0.1\),  \(\gamma =0.05\), like in the example of solutions to (2+1)-dimensional KdV equation, presented in [23]. Take \(k=1\), permissible by (57). Then from (55)  \(l\approx \pm 0.7969\),  \(\omega \approx 1.253\) from (56), and  \(A_{2}\approx 1.11343\). The snapshot of the wave is presented in Fig. 1.

Fig. 1
figure 1

Snapshot of the soliton solution \(A\,\text {sech}(\xi )^{2}\) to (2+1)-dimensional KdV2 equation in two space dimensions. For parameters used in this example, see details in the text

Full size image

Remark 1

It is worth noting that if we assume \(l=0\) in the soliton solution (46), then from Eqs. (51–53), we obtain exactly the same solution as that in Sect. IV in the paper [27] for one-dimensional extended KdV Eq. (39). This means that the family of soliton solutions to (2+1)-dimensional, extended KdV Eq. (38) is much wider (solutions with \(l\ne 0\) are allowed) than the family of solutions to one-dimensional extended KdV Eq. (39).

In Fig. 2, we compare profiles of two particular solutions to (2+1)-dimensional, extended KdV Eq. (38) in the case when \(\alpha =0.15\),  \(\beta =0.1\),  \(\gamma =0.05\). The blue line presents the solution with \(k=k_{\text {max}}\), \(l=0\), which is simultaneously the solution to the one-dimensional extended KdV Eq. (39). The yellow line corresponds to the solution to Eq. (38) with \(k=1\), \(l=0.7969\). Note that in the latter case, the soliton profile is plotted versus rotated coordinate \(x'\) (see Sect. 5). The velocities of these waves are also different. They are \(v_{\text {blue}}=1.11455\) and \(v_{\text {yellow}}=0.987877\), respectively. In general, \(v_{l=0} > v_{l\ne 0}\).

Fig. 2
figure 2

Comparison of the profile of the soliton solution with \(k=1\), \(l=0.7969\) (yellow line), shown in Fig. 1 with the profile of the solution with \(k=k_{\text {max}}\), \(l=0\) (blue line)

Full size image

4.2 Periodic cnoidal solutions

In [33], Dingemans showed in detail that by performing direct integration of the KdV equation and keeping non-zero integration constants, one arrives at periodic solutions of the type \(\eta = A\,\text {cn}^{2}[B(x-vt),m]+B\), where negative B assures conservation of the volume of fluid displaced from the equilibrium level. Therefore, the physically relevant solution to the (2+1)-dimensional, extended KdV equation has to contain analogous term.

Assume solutions in the same form as those to the KdV equation that is,

$$\begin{aligned} \eta (x,y,t)= & {} A\, \text {cn}^{2} [(k x+l y-\omega t),m]+B \nonumber \\= & {} A\,\text {cn}^{2} (\xi ,m)+B,\quad m\in (0,1), \end{aligned}$$
(58)

where the value of B has to ensure that the volumes of elevated and depressed fluid cancel over the intervals equal to wavelengths. This condition reads as

$$\begin{aligned}{} & {} \int _{0}^{L_{x}} \int _{0}^{L_{y}}( A\, \text {cn}^{2} [(k x+l y-\omega t),m]+B)\, \nonumber \\{} & {} dx\,dy=0, \end{aligned}$$
(59)

where \(L_{x},L_{y}\) are wavelengths in x, y directions, respectively. Periodicity of the function \(\text {cn}^{2}[(k x+l y-\omega t),m]\) implies

$$\begin{aligned} L_x=\frac{2 K(m)}{k} \qquad \text{ and } \qquad L_y=\frac{2 K(m)}{l}, \end{aligned}$$

where K(m) is the complete elliptic integral of the first kind. So, (59) gives

$$\begin{aligned} B&=- \frac{A}{L_{x}\,L_{y}} \int _{0}^{L_{x}}\! \int _{0}^{L_{y}} \text {cn}^{2} [(k x+l y-\omega t),m] =\nonumber \\&\quad -\frac{A}{m}\left( \frac{E(m)}{K(m)}+m-1\right) , \end{aligned}$$
(60)

where E(m) is the complete elliptic integral.

Inserting (58) into (45) yields after simplifications

$$\begin{aligned}&-2 A \text {cn}(\xi ,m) \text {dn}(\xi ,m) \text {sn}(\xi ,m) \nonumber \\&\quad \times \bigg [ \text {A1} +8\text {A2}m -4\text {A2}+\text {A3} B+\text {A4} B^2 -2 A \text {A5} m\nonumber \\&+2 A \text {A5}+8 \text {A6} B m -4 \text {A6} B +136 \text {A7} m^2-136 \text {A7} m \nonumber \\&+16 \text {A7}+\text {A8} B +\text {cn}(\xi ,m)^2 \left( A \text {A3}+2 A \text {A4} B \right. \nonumber \\&+8 A \text {A5} m-4 A \text {A5} +8 A \text {A6} m-4 A \text {A6} +A \text {A8}\nonumber \\&\left. -12 \text {A2} m-12 \text {A6} B m-480 \text {A7} m^2+240 \text {A7} m\right) \nonumber \\&+ \text {cn}(\xi ,m)^4 \left( A^2 \text {A4}-6 A \text {A5} m-12 A \text {A6} m+360 \text {A7} m^2\right) \bigg ] {=}0. \end{aligned}$$
(61)

Equation (61) is satisfied when simultaneously

$$\begin{aligned}&\text {A1} +8\text {A2}m -4\text {A2}+\text {A3} B+\text {A4} B^2\nonumber \\&-2 A\text {A5} m+2 A \text {A5}+8 \text {A6} B m \end{aligned}$$
(62)
$$\begin{aligned}&-4 \text {A6} B +136 \text {A7} m^2-136 \text {A7} m+16 \text {A7}+\text {A8} B =0, \nonumber \\&A \text {A3}+2 A \text {A4} B+8 A \text {A5} m-4 A \text {A5}+8 A \text {A6} m-4 A \text {A6} \end{aligned}$$
(63)
$$\begin{aligned}&+A \text {A8}-12 \text {A2} m-12 \text {A6} B m-480 \text {A7} m^2+240 \text {A7} m =0, \nonumber \\&\text{ and } A^2 \text {A4}-6 A \text {A5} m-12 A \text {A6} m+360 \text {A7} m^2 =0. \end{aligned}$$
(64)

Now, we come back from notations \(\text {A1}-\text {A8}\) to their original values according to Eq. (45). Then equations (62)-(64) take the following form

$$\begin{aligned}&-\frac{1}{12} \beta k^3 (-23 \alpha A+23 \alpha A m+20 \alpha B-8 m (5 \alpha B+2)+8) \end{aligned}$$
(65)
$$\begin{aligned}&-\frac{1}{8} k \left( 3 \alpha ^2 B^2-12 \alpha B+8 \gamma l^2 (1-2 m)-8\right) +\frac{\gamma l^2 (3 \alpha B+1)}{2 \beta k} \nonumber \\&\quad +\frac{19}{45} \beta ^2 k^5 \left( 17 m^2-17 m+2\right) -\frac{\gamma ^2 l^4}{8 \beta ^2 k^3}-\omega =0, \nonumber \\&\frac{\alpha A}{4 \beta k} \left( -3 \beta k^2 (\alpha B-2)+22 \beta ^2 k^4 (2 m-1)+6 \gamma l^2\right) \nonumber \\&\quad -\frac{1}{3} k m \left( 3 \beta k^2 (5 \alpha B+2)+38 \beta ^2 k^4 (2 m-1)+9 \gamma l^2\right) =0, \end{aligned}$$
(66)
$$\begin{aligned}&-\frac{3}{8} \alpha ^2 A^2 k-\frac{43}{4} \alpha A \beta k^3 m+19 \beta ^2 k^5 m^2 = 0. \end{aligned}$$
(67)

Equation (67) has two roots analogous to those in (54)

$$\begin{aligned}{} & {} A_{1}=\frac{\beta k^{2} m}{3\alpha }(-43-\sqrt{2305}), \qquad \nonumber \\{} & {} A_{2}=\frac{\beta k^{2}m}{3\alpha }(-43+\sqrt{2305}). \end{aligned}$$
(68)

Inserting B given by (60) into (66), we can obtain \(l^{2}\) as

$$\begin{aligned} l^{2}&= -\beta k \bigg [(9 \alpha ^2 A^2 k -9 \alpha ^2 A^2 k m -9 \alpha ^2 A^2 k \frac{E(m)}{K(m)}\nonumber \\&-192 \alpha A \beta k^3 m^2 +126\alpha A \beta k^3 m \nonumber \\&-18 \alpha A k m -60 \alpha A \beta k^3 m \frac{E(m)}{K(m)}\nonumber \\&+304 \beta ^2 k^5 m^3 -152 \beta ^2 k^5 m^2 +24 \beta k^3 m^2 \bigg ] \nonumber \\&\bigg {/} \bigg [ 18 \gamma m \left( 2 \beta k^2 m-\alpha A \right) \bigg ]. \end{aligned}$$
(69)

Then with B given by (60) and \(l^{2}\) given by (69), we obtain from (65)

$$\begin{aligned} \omega =&\frac{k}{12960 m^2 \left( \alpha A-2 \beta k^2 m\right) ^2} \nonumber \\&\bigg [45 \alpha ^2 A^2 \frac{E(m)^2}{K(m)^2} \left( 99 \alpha ^2 A^2+1320 \alpha A \beta k^2 m\right. \nonumber \\&\left. -3712 \beta ^2 k^4 m^2\right) \nonumber \\&+30 \alpha A \frac{E(m)}{K(m)} \bigg (297 \alpha ^3 A^3 (m-1)\nonumber \\&+18 \alpha ^2 A^2 m \left( \beta k^2 (358 m-289)-9\right) \nonumber \\&-24 \alpha A \beta k^2 m^2 \!\left( \!16 \beta k^2 (77 m-53)+15\!\right) \!\nonumber \\&+32 \beta ^2 k^4 m^3 \left( 437 \beta k^2 (2 m-1)+33\right) \!\bigg ) \nonumber \\&+4455 \alpha ^4 A^4 (m-1)^2+540 \alpha ^3 A^3 (m-1) m\nonumber \\&\left( \beta k^2 (202 m-179)-9\right) \nonumber \\&-36 \alpha ^2 A^2 m^2 \left( \beta ^2 k^4 \left( 22356 m^2-34676 m+13941\right) \right. \nonumber \\&\left. +30 \beta k^2 (84 m-47)-135\right) \nonumber \\&+96 \alpha A \beta k^2 m^3\!\left( \beta ^2 k^4 \!\left( 16529 m^2\!-20899 m+7089\right) \!\right. \nonumber \\&\left. +15 \beta k^2 (236 m-129)\!-270\right) \nonumber \\&-64 \beta ^2 k^4 m^4 \left( 19 \beta ^2 k^4 \left( 794 m^2-794 m+239\right) \right. \nonumber \\&\left. +2280 \beta k^2 (2 m-1)-495\right) \bigg ]. \end{aligned}$$
(70)

4.2.1 Case  \(A=A_{1}=\displaystyle \frac{\beta k^{2} m}{3\alpha }(-43-\sqrt{2305})\approx (-91.01)\frac{\beta k^{2} m}{3\alpha }\)

For \(A=A_{1}\), we have

$$\begin{aligned} l^{2} = \frac{\beta k^2 \left[ \left( 549 + 11 \sqrt{2305}\right) \beta k^2\left( 3 \frac{E(m)}{K(m)}+m-2\right) -3 \left( 47+\sqrt{2305}\right) \right] }{3 \left( 49+\sqrt{2305}\right) \gamma }. \end{aligned}$$
(71)

For real l, there must be

$$\begin{aligned}{} & {} F(m):= 3 \frac{E(m)}{K(m)}+m-2 \ge \frac{3 \left( 47+\sqrt{2305}\right) }{\left( 549+11 \sqrt{2305}\right) \beta k^2}\nonumber \\{} & {} \approx \frac{0.264625}{\beta \,k^2}. \end{aligned}$$
(72)
Fig. 3
figure 3

Graph of the function F(m), defined in (72), \(m\in [0,1)\)

Full size image

The graph of the function \(F(m), m\in [0,1)\) is shown in Fig. 3. Function  \(1\!\ge \! F(m)\!>0\!\) for  \(m\in [0,m_{s})\), where \(m_{s}\approx 0.9611495\). Therefore, in the interval \(m\in [0,m_{s})\) there is some range of allowed k. Let us take the same example of physical parameters \(\alpha =0.15, ~\beta =0.1, ~\gamma =0.05\). From (72), we have  \(k^{2}>\frac{0.264625}{\beta F(m)}=\frac{2.64625}{F(m)}\). Taking for example \(m=\frac{1}{3}\) we obtain this condition as  \(k^{2}> 3.27489\). Take allowed  \(k=2\). So, with above parameters we get  \(A \approx -26.966\),  \(B\approx 12.8011\),  \(l\approx 1.31714\) and  \(\omega \approx 0.985515\). A snapshot of this wave, with the abovementioned parameters, is shown in Fig. 4. In this case, fluid is depressed in crests and elevated in troughs relative to the equilibrium level.

However, it follows from the scaling (5) that the wave amplitude (in the scaled variables) should be close to 1. The solutions obtained with root \(A_{1}\) with realistic values of \(\alpha , \beta , \gamma \) have too large amplitudes, so they are unphysical. Similar properties were observed in the case of cnoidal solutions to the extended KdV equation (one dimensional) in [28]. Solutions corresponding to \(A=A_{1}\) root also had unphysically large amplitudes. Only when \(m\rightarrow 0\) the amplitude of solutions corresponding to the root \(A_{1}\) can be close to 1. But for m close to 0, the wave profile tends to the cosine function.

No such objections exist to the solutions obtained with root \(A_{2}\), as shown in the next subsection.

Fig. 4
figure 4

Snapshot of the example of periodic solution  \(A_{1}\,\text {cn}(\xi )^{2}+B\)  to (2+1)-dimensional KdV2 equation in two space dimensions. For parameters used in this example, see details in the text

Full size image

4.2.2 Case  \(A=A_{2}=\displaystyle \frac{\beta k^{2}m}{3\alpha }(-43+\sqrt{2305})\approx 5.01 \frac{\beta k^{2}m}{3\alpha }\)

Inserting \(A=A_{2}\) and B given by (60) into (69) yields

$$\begin{aligned} l^{2}_{A=A_{2}}&= \frac{\beta k^2 \left( \beta k^2 \left( 11 \sqrt{2305}-549\right) \left( 3\frac{E(m)}{K(m)}+m-2\right) -3 \sqrt{2305}+141\right) }{3 \left( \sqrt{2305}-49\right) \gamma } \nonumber \\&\approx \frac{\beta k^2 }{\gamma }\left( 7.03508\, \beta k^2\left( 3\frac{E(m)}{K(m)}+m-2\right) + 1.02105 \right) . \end{aligned}$$
(73)

As earlier, denote  \(\displaystyle F(m)= 3\frac{E(m)}{K(m)}+m-2\). For real l, there must be  \(\displaystyle k^{2} F(m)>-\frac{0.145137}{\beta }\). For \(m\rightarrow 1, ~F(m)\rightarrow -\infty \). \(F(m_{s})=0\)  for  \(m_{s}\approx 0.9611495\). Therefore, for  \( m_{s}< m <1 \),  \(l^{2}\) is positive for arbitrary k.

With \(l^{2}\) given by (73) and \(A=A_{2}\), we obtain from (65)

$$\begin{aligned} \omega&= \frac{1}{180 \left( \sqrt{2305}-49\right) ^2 }\nonumber \\&\quad \times \bigg [ \beta ^2 k^5 \left( 19 \left( 4241 \sqrt{2305}-203727\right) m^2\right. \nonumber \\&\quad \left. +4 \left( 192629\sqrt{2305}-9246043\right) m \right. \nonumber \\&\left. \quad -770516 \sqrt{2305}+36984172\right) \nonumber \\&\quad -570\left( 95 \sqrt{2305}-4561\right) \beta k^2 (m-2) \nonumber \\&\quad -6885 \sqrt{2305}+330795 -10 \beta k^3 \frac{E(m)}{K(m)} \nonumber \\&\quad \times \left( \left( 170219 \sqrt{2305}-8170997\right) \beta k^2 (m-2)\right. \nonumber \\&\quad \left. +171 \left( 95 \sqrt{2305}-4561\right) \right) \nonumber \\&\quad -15 \left( 170219 \sqrt{2305}-8170997\right) \beta ^2 k^5 \frac{E(m)^2}{K(m)^{2}}\bigg ] . \end{aligned}$$
(74)

Let us consider the same example of physical parameters \(\alpha =0.15, ~\beta =0.1, ~\gamma =0.05\). Take \(m=0.99\) and \(k=1\). Then  \(A\approx 1.10229\),  \(B\approx -0.294965\),  \(l\approx 1.33471\) and  \(\omega \approx 1.37342\). The snapshot of the wave \(\eta =A\, \text {cn}^{2}(kx+ly-\omega t) +B\) with the above constants is presented in Fig. 5. Note that in this case fluid is elevated in crests and depressed in troughs relative to zero level.

4.3 Superposition solutions

Recently, Khare and Saxena [34,35,36] demonstrated that for several nonlinear evolution equations which admits solutions in terms of elliptic functions \(\text {dn}(x,m), \text {cn}(x,m)\) there exist solutions in terms of their superpositions \(\text {dn}(x,m)\pm \sqrt{m}\,\text {cn}(x,m)\). In 2013, Khare and Saxena [34] for the first time showed that the function of the form

$$\begin{aligned}{} & {} \eta (x,t)=\frac{A}{2}\left[ \text {dn}^{2}(D(x-vt),m)\pm \sqrt{m}\,\text {cn}(D(x-vt),m)\,\right. \nonumber \\{} & {} \left. \text {dn}(D(x-vt),m)\right] , \end{aligned}$$
(75)

were A, D, v are constants, fulfils the Korteweg-de Vries equation. This result inspired us to demonstrate that the analogous solutions exist for the extended KdV equation (KdV2), both in the form (75) [30], and in the form

$$\begin{aligned}{} & {} \eta (x,t)=\frac{A}{2}\left[ \text {dn}^{2}(D(x-vt),m)\,\right. \nonumber \\{} & {} \left. \pm \sqrt{m}\text {cn}(D(x-vt),m)\,\text {dn}(D(x-vt),m)\right] +B, \nonumber \\ \end{aligned}$$
(76)

which assures that overall volume of the displaced fluid is zero [31]. Below, we check whether analogous solutions exist for (2+1)-dimensional extended KdV Eq. (38).

Fig. 5
figure 5

Snapshot of the example of periodic solution \(A_{2}\,\text {cn}(\xi )^{2}+B\) to (2+1)-dimensional KdV2 equation in two space dimensions. For parameters used in this example, see details in the text

Full size image

It is worth noting, that due to properties of Jacobi elliptic functions, waves represented by  \(\text {dn}(x,m) + \sqrt{m}\,\text {cn}(x,m)\) and by  \(\text {dn}(x,m) - \sqrt{m}\,\text {cn}(x,m)\) describe the same profile, only shifted by a half of the wavelength. Therefore, it is sufficient to examine the function with one sign.

In this section, we assume superposition solutions in the form which preserve the volume of the displaced fluid

$$\begin{aligned} \eta (x,y,t)&=\frac{A}{2}\left[ \text {dn}^{2} (\xi ,m)\pm \sqrt{m}\,\text {cn}(\xi ,m)\,\text {dn}(\xi ,m) \right] +B,\nonumber \\&m\in (0,1),\qquad \xi = k x+l y-\omega t. \end{aligned}$$
(77)

Volume conservation requires

$$\begin{aligned} \int _{0}^{L_{x}} \int _{0}^{L_{y}}\eta (x,y,t)\, dx\,dy=0. \end{aligned}$$
(78)

Periodicity of the \((\text {dn}^{2}[(k x+l y-\omega t),m] \pm \sqrt{m}\,\text {cn} [(k x+l y-\omega t),m]\,\text {dn} [(k x+l y-\omega t),m])\) function implies

$$\begin{aligned} L_x=\frac{4 K(m)}{k} \qquad \text{ and } \qquad L_y=\frac{4 K(m)}{l}, \end{aligned}$$

where K(m) is the complete elliptic integral of the first kind. So, from (78) we obtain

$$\begin{aligned} B&=-\frac{1}{L_{x}L_{y}} \int _{0}^{L_{x}}\!\! \int _{0}^{L_{y}} \frac{A}{2} \bigg (\text {dn}^{2} [(k x+l y-\omega t),m] \nonumber \\&\pm \sqrt{m}\,\text {cn} [(k x+l y-\omega t),m]\,\text {dn} [(k x+l y-\omega t),m]\bigg ) \,\nonumber \\&dx\,dy = -\frac{A\, E(m)}{2\,K(m)} , \end{aligned}$$
(79)

where E(m) is the complete elliptic integral.

Inserting (77) into (45) and simplifying yields equation of the following form (arguments of the elliptic functions are omitted)

$$\begin{aligned}&\text {sn}\left( C_{0} +C_{11}\,\text {cn}\,\text {dn}+C_{2}\,\text {cn}^{2} +C_{31}\,\text {cn}^{3}\text {dn}+C_{4}\,\text {cn}^{4}+C_{51}\,\right. \nonumber \\&\left. \text {cn}^{5}\text {dn}+C_{6}\,\text {cn}^{6}\right) =0, \end{aligned}$$
(80)

which is equivalent to seven equations \(C_{i}=0\) type.

We search for solutions with \(m\in (0,1)\). Equations \(C_{51}=0\) and \(C_{6}=0\) give the same condition, equivalent to (51)

$$\begin{aligned} \frac{3}{8} \alpha ^2 A^2 k+\frac{43}{4} \alpha A \beta k^3-19 \beta ^2 k^5 =0, \end{aligned}$$

and then have the same roots of A as (54), that is,

$$\begin{aligned}{} & {} A_{1}=\frac{\beta k^{2}}{3\alpha }(-43-\sqrt{2305}), \\{} & {} A_{2}=\frac{\beta k^{2}}{3\alpha }(-43+\sqrt{2305}). \end{aligned}$$

Equations \(C_{0}=0\) to \(C_{4}=0\) receive the following form

$$\begin{aligned} C_{0} =&~ 0 = \frac{(m-1)}{24 \beta ^2 k^3} \bigg [135 \alpha ^2 A^2 \beta ^2 k^4 \frac{E(m)^2}{K(m)^2} \nonumber \\&+30 \alpha A \beta k^2 \left( \beta k^2 \left( 9 \alpha A (m-1)+10 \beta k^2 (5 m-1)+36\right) \right. \nonumber \\&\left. +36 \gamma l^2\right) \frac{E(m)}{K(m)} \nonumber \\&+ \bigg (60\beta ^3 k^6 (5 \alpha A+m (\alpha A (48 m-53)-20)+4)\nonumber \\&+180 \gamma ^2 l^4 \nonumber \\&+45 \beta ^2 k^4 \left( 3 \alpha A (m-1) (\alpha A (m-1)+8)\right. \nonumber \\ {}&\left. +8 \left( \gamma l^2-4\right) -40 \gamma l^2 m\right) \nonumber \\&+360 \beta \gamma k^2 l^2 (3 \alpha A (m-1)-2)-76 \beta ^4 k^8 (m (61 m-46)+1)\nonumber \\&+1440 \beta ^2 k^3 \omega \bigg )\bigg ], \end{aligned}$$
(81)
$$\begin{aligned} C_{11} =&~ 0 = -\frac{\sqrt{m}}{12 \beta ^2 k^3 } \bigg [ 135 \alpha ^2 A^2 \beta ^2 k^4 \frac{E(m)^2}{K(m)^2} \nonumber \\&+15 \alpha A \beta k^2 \left( 9 \beta k^2 (3 \alpha A (m-1)+8)\right. \nonumber \\&\left. +80 \beta ^2 k^4 (2 m-1)+72 \gamma l^2\right) \frac{E(m)}{K(m)} \nonumber \\&+ \bigg (90 \beta ^2 k^4 \left( 3 \alpha ^2 A^2 (m-1)^2+18 \alpha A (m-1)\right. \nonumber \\&\left. +16 l^2 (\gamma -2 \gamma m)-16\right) \nonumber \\&+15 \beta ^3 k^6 \left( 113 \alpha A+417 \alpha A m^2-2 m ( 265 \alpha A+64)+64\right) \nonumber \\&+180 \gamma ^2 l^4 \nonumber \\&+180 \beta \gamma k^2 l^2 (9 \alpha A (m-1)-4)-608 \beta ^4 k^8 \left( 17 m^2\!-17 m+2\right) \nonumber \\&+1440 \beta ^2 k^3 \omega \bigg )\bigg ], \end{aligned}$$
(82)
$$\begin{aligned}&C_{2} = ~ 0 = -\frac{m}{24 \beta ^2 k^3 } \bigg [ 270 A^2 k^4 \alpha ^2 \beta ^2 \frac{E(m)^2}{K(m)^2} \nonumber \\&+ 30 A k^2 \alpha \beta \left( k^2 \beta (72 + 45 A (-1 + m) \alpha \right. \nonumber \\&\left. + 40 k^2 (-5 + 7 m) \beta ) + 72 l^2 \gamma \right) \frac{E(m)}{K(m)} \nonumber \\&+ \bigg (120 k^6 \beta ^3 \left( 40 - 56 m + A\alpha (-1 + m) (-107 + 249 m) \right) \nonumber \\&- 152 k^8 \beta ^4 (91 + m (-406 + 331 m))\nonumber \\&+ 360 k^2 l^2 \beta \gamma (-4 + 15 A \alpha (-1 + m)) \nonumber \\&+ 360 l^4 \gamma ^2 + 45 k^4 \beta ^2 (3 A\alpha (-1 + m) (40 + 9 A \alpha (-1 + m)) \nonumber \\&- 224 l^2 m \gamma + 32 (-2 + 5 l^2 \gamma )) +2880 k^3 \beta ^2 \omega \bigg ) \bigg ], \end{aligned}$$
(83)
$$\begin{aligned} C_{31}&= 0 = \frac{5 m^{3/2}}{2\beta k} \bigg [6 \alpha A \beta k^2 \left( 3 \alpha A+20 \beta k^2\right) \frac{E(m) }{K(m)}\nonumber \\&\quad + 27\alpha ^2 A^2 \beta k^2 (m-1) \nonumber \\&\quad +12 \alpha A \left( \beta ^2 k^4 (59 m-37)\right. \nonumber \\&\quad \left. +6 \beta k^2+6 \gamma l^2\right) \nonumber \\&\quad -16 \beta k^2 \left( 38 \beta ^2 k^4 (2 m-1)\right. \nonumber \\&\quad \left. +6 \beta k^2+9 \gamma l^2\right) \bigg ], \end{aligned}$$
(84)
$$\begin{aligned} C_{4} =&0 = \frac{5 m^2}{k} \! \bigg [18 \alpha ^2 A^2 k^{2} (m\!-\!1)\!\nonumber \\&\quad +\!3 \alpha A k^{2} \! \left( 3 \alpha A\!+\!20 \beta k^2\right) \! \frac{E(m)}{K(m)} \!+\!36 \alpha A \! \left( \!k^{2}\!+\!\frac{\gamma l^2}{\beta }\!\right) \nonumber \\&\quad +3 \alpha A \beta k^4 (161 m-117)\nonumber \\&\quad -76 \beta ^2 k^6 (11 m-7)-48 \beta k^4-72 \gamma k^2 l^2 \bigg ] \end{aligned}$$
(85)

Equations (81–85) are complicated. Therefore, we will separately consider cases \(A=A_{1}\) and \(A=A_{2}\). Then it appears that for fixed \(A_{i}\) some pairs of above equations boil down to the same conditions when \(m\ne 0\) and \(m\ne 1\).

4.3.1 Case  \(A=A_{1}=\displaystyle \frac{\beta k^2}{3 \alpha } \left( -43-\sqrt{2305}\right) \approx (-91.01) \frac{\beta k^{2}}{3\alpha }\)

Substituting  \(A=A_{1}\) into (84) and into (85) and solving the resulting equations for \(l^{2}\) yields the same condition

$$\begin{aligned} l^2 =&\frac{\left( 549+11 \sqrt{2305}\right) \beta ^2 k^4 }{12 \left( 49+\sqrt{2305}\right) \gamma }\left( 6\frac{E(m)}{ K(m)}+m-5\right) \nonumber \\&-\frac{\left( 47+\sqrt{2305}\right) \beta k^2}{\left( 49+\sqrt{2305}\right) \gamma } . \end{aligned}$$
(86)

For  \(l^{2}>0\), there must be

$$\begin{aligned} \left( 6\frac{E(m)}{K(m)}+m-5 \right)&:= G(m) > \frac{12(47+\sqrt{2305})}{(549+11 \sqrt{2305})\beta k^2 }\nonumber \\&\approx \frac{1.0585}{\beta k^2}. \end{aligned}$$
(87)

Plot of the function  \(G(m)=6\frac{E(m)}{K(m)}+m-5\)  is shown in Fig. 6. Its root is \(m_{r}\approx 0.449834\). It is clear that l can be real and \(|l|>0\) only if  \(0<m < m_{r}\). In such case, \(k^{2} > \frac{1.0585}{G(m) \beta }\).

It turns out that with \(l^{2}\) given by (86) and \(m\in (0,1)\) Eqs. (81–83) reduce to the same condition, which gives finally

$$\begin{aligned} \omega =&~\frac{k}{5760 \left( 2353+49 \sqrt{2305}\right) }\nonumber \\ {}&\quad \times \bigg [ \bigg (- \left( 19 (203727+4241 \sqrt{2305}) m^2 \right. \nonumber \\&\left. \quad +(381031262+7936866 \sqrt{2305}) m\right. \nonumber \\ {}&\quad \left. - 6728181 \sqrt{2305}-322969067 \right) \nonumber \\&\quad +20 (8170997\!+\!170219 \sqrt{2305}) (m-5) \frac{E(m)}{K(m)} \nonumber \\&\quad +60\left( 8170997\!+\!170219 \sqrt{2305}\right) \frac{E(m)^2}{K(m)^2} \bigg )\beta ^2 k^4 \nonumber \\&\quad + 2280 \left( 4561+95 \sqrt{2305}\right) \left( 6\frac{E(m)}{K(m)}+ m-5\right) \nonumber \\ {}&\quad \times \beta k^2 +720 (7351+153 \sqrt{2305}) \bigg ]. \end{aligned}$$
(88)
Fig. 6
figure 6

Graph of the function \(G(m), m\in [0,1)\)

Full size image

Example: Let us check a particular case  \(\alpha =0.15, ~\beta =0.1, ~\gamma =0.05\). Condition (87) for real value of l permits for \(\beta \, k^{2}> \frac{1.0585}{G(m)}\) and \(G(m)>0\). So, \(\beta \,k^{2}\) cannot be less than 1.0585. This condition makes \(A_{1}>>1\) and therefore solutions with \(A=A_{1}\) are unphysical. Again this property is analogous to that observed in [31] for superposition solutions to the extended KdV equation (one dimensional).

4.3.2 Case  \(A=A_{2}=\displaystyle \frac{\beta k^2}{3 \alpha }\left( -43+\sqrt{2305}\right) \approx 5.01 \frac{\beta k^{2}}{3\alpha }\)

In this case, the condition obtained from both (84) and (85) equations is

$$\begin{aligned} l^2&= \frac{\left( 11 \sqrt{2305}-549\right) \beta ^2 k^4 }{12 \left( \sqrt{2305}-49\right) \gamma }\left( 6\frac{E(m)}{ K(m)}+m-5\right) \nonumber \\&-\frac{\left( \sqrt{2305}-47\right) \beta k^2}{\left( \sqrt{2305}-49\right) \gamma } . \end{aligned}$$
(89)

For  \(l^{2}>0\), there must be

$$\begin{aligned}&\left( 6\frac{E(m)}{K(m)}+m-5 \right) > \frac{12(\sqrt{2305}-47)}{(11 \sqrt{2305}-549)\beta k^2 }\nonumber \\&\approx -\frac{0.580548}{\beta k^2}. \end{aligned}$$
(90)

It is clear from the graph of G(m) that the condition (90) permits for a wide range of \(m\in (0,m_{up})\) where \(m_{up}\) is the root of the equation  \(G(m)-\frac{12(\sqrt{2305}-47)}{(11 \sqrt{2305}-549)\beta k^2}=0\). In particular, values of m close to 1 are allowed.

Similarly like in the previous subsection, Eqs. (81–83) with \(l^{2}\) given by (89) boil down to the same condition, which gives finally

$$\begin{aligned} \omega =&~ \frac{k}{5760 \left( 49 \sqrt{2305}-2353\right) }\nonumber \\ {}&\quad \times \bigg [ \bigg ( \left( (3870813-80579 \sqrt{2305}) m^{2} \right. \nonumber \\&\left. +(381031262-7936866 \sqrt{2305})m\right. \nonumber \\&\left. +6728181\sqrt{2305}-322969067\right) \nonumber \\&+20 (170219 \sqrt{2305}-8170997) (m-5) \frac{E(m)}{K(m)} \nonumber \\&+60 \left( 170219 \sqrt{2305}-8170997\right) \frac{E(m)^2}{K(m)^2}\bigg ) \beta ^2 k^4 \nonumber \\&+2280 \left( 95 \sqrt{2305}\!-4561\right) \left( 6 \frac{E(m)}{K(m)}\!+\!m\!-\!5\right) \beta k^2 \!\nonumber \\&+ 720 \left( 153\sqrt{2305}\!-7351\right) \bigg ] . \end{aligned}$$
(91)

Let us present an example of a superposition solution. Assume as previously, \(\alpha =0.15\), \(\beta =0.1\), \(\gamma =0.05\). A nice wave profile can be obtained with \(m=0.99\). In such a case for \(l^{2}>0\), there must be \(k^{2}< 2.45943\). Take, for instance, permissible \(k=1\). Then \(l\approx 0.0348\). \(A_{2}\approx 1.11343\)., \(B\approx -0.153\), \(\omega \approx 1.33381\). The profile of the wave with the above parameters is displayed in Fig. 7.

Fig. 7
figure 7

Snapshot of the example of superposition solution  \(\frac{A_{2}}{2}\left[ \text {dn}(\xi )^{2}+\sqrt{m}\text {cn}(\xi )\text {dn}(\xi )\right] +B\)  to (2+1)-dimensional KdV2 equation in two space dimensions. For parameters used in this example, see details in the text

Full size image

Remark 2

In many studies focusing on the mathematical structure of solutions, the constant term B is neglected in periodic solutions. We have also carried out detailed considerations for both cnoidal solutions and superposition solutions without this term. They are not presented here because the results are qualitatively similar. This means that there exist families of solutions to (2+1)-dimensional, extended KdV equation in the form

$$\begin{aligned}{} & {} \eta =A_{2} \text {cn}^{2}(\xi ,m) \qquad \text{ and }\nonumber \\{} & {} \qquad \eta =\frac{A_{2}}{2}\left[ \text {dn}^{2} (\xi ,m)\pm \sqrt{m}\,\text {cn}(\xi ,m)\,\text {dn}(\xi ,m) \right] , \end{aligned}$$

for some ranges of relevant parameters. In these cases, too, only solutions with \(A=A_{2}\) are physically meaningful.

5 Summary of solutions

Formally, all analytic solutions found in this paper are, similarly like solutions to (2+1)-dimensional KdV equation found in [23], are (2+1)-dimensional. However, despite explicit dependence on x, y coordinates, they describe one-dimensional motion. This property is easily seen when we introduce \(x',y'\) coordinates, rotated to x, y by the angle \(\varphi =\arctan (\frac{l}{k})\). In these rotated coordinates, we have

$$\begin{aligned} \eta (kx+ly-\omega t)&=\eta \big (k(x'\cos \varphi -y'\sin \varphi )\nonumber \\&+l(x'\sin \varphi +y'\cos \varphi )-\omega t) \big ) \nonumber \\&=\eta (\sqrt{k^{2}+l^{2}}\,x'-\omega t). \end{aligned}$$
(92)

The wave represented by the function (92) propagates in \(x'\)-direction, maintaining translational symmetry in the perpendicular \(y'\)-direction. This property is the source of success of the much simpler (1+1)-dimensional theory.

In Fig. 8, we collected all three examples of solutions presented earlier in 3D plots in Figs. 1, 5 and 7, that is, those which correspond to appropriate \(A_{2}\) roots.

Fig. 8
figure 8

Snapshots of examples of solutions to (2+1)-dimensional extended KdV1 Eq. (38) in rotated (scaled) coordinates. The soliton solution of Fig. 1 is shown with a blue line, the cnoidal one from Fig. 5 with a red line and the superposition solution of Fig. 7 with a green line

Full size image

In [23], we discussed the solutions to Eq. (16), i.e., the (2+1)-dimensional KdV equation. This equation has the same three families of analytic solutions, namely soliton solutions, periodic cnoidal solutions and periodic superposition solutions. The two parameters, k and l, can be arbitrary in each solution. The (2+1)-dimensional, extended KdV equation (38) imposes more stringent conditions on the families of solutions, leaving only k as arbitrary in a certain interval.

6 Conclusions

In this article, we derived a highly nonlinear, nonlocal (2+1)-dimensional, extended KdV (KdV2) equation. Moreover, we proved that three families of analytic solutions exist for that equation, even though it is highly nonlinear and nonintegrable. In particular cases, when \(l=0\) is set in soliton solutions, (2+1)-dimensional, extended KdV equation provides that solutions become identical to solutions to one-dimensional extended KdV equation derived by Marchant and Smyth in 1990 [26].

In the case of the one-dimensional extended KdV (KdV2) equation, which is also nonintegrable, we found so-called adiabatic invariants in [37, 38]. Moreover, in [38], adapting near identity transformation (NIT in short) introduced by Kodama [39, 40], we obtained NIT-transformed KdV2 equation in Hamiltonian form. Therefore, a search for adiabatic invariants of the new (2+1)-dimensional extended KdV (KdV2) equation and its approximate Hamiltonian form will be the next step to study.

For the time being, it also remains to be seen whether there are other solutions to both the (2+1)-dimensional KdV equation and the (2+1)-dimensional, extended KdV equation than the essentially one-dimensional ones found in [23] and in the present work.