Global stability of road vehicle motion with driver control

Abstract

The paper contributes to unveil how drivers—either human or not—may lose control of road vehicles after a disturbance. First, a simple vehicle-and-driver model is considered: Its motion is characterized by the existence of limit cycles whose amplitude depend on vehicle forward velocity (both oversteering and understeering vehicles may exibit this property). Such limit cycles are originated by a Hopf bifurcation occurring at a relatively high vehicle forward velocity. A mathematical proof of the existence of Hopf bifurcations is given. The existence of Hopf bifurcations and saddle limit cycles is confirmed by experimental tests performed by a dynamic driving simulator with a complex vehicle model and human in the loop. By a Zubov method, a Lyapunov function is derived to compute the region of asymptotic stability for the simple vehicle-and-driver model. A necessary and sufficient condition is derived for global asymptotic stability. Such a condition refers to the variation of the kinetic energy which must vanish at the end of the disturbed motion. This occurrence has been detected at the driving simulator too. Just a single stable equilibrium has been found inside the domain of attraction in all of the examined cases.

1 Introduction

The global stability of the motion of road vehicles is currently not studied with much detail. Nonetheless understanding how drivers lose control is of crucial importance to prevent road accidents [1]. According to World Health Organization [2] “Every year the lives of approximately 1.3 million people are cut short as a result of a road traffic crash. Between 20 and 50 million more people suffer non-fatal injuries, with many incurring a disability as a result of their injury. Road traffic crashes cost most countries 3% of their gross domestic product.”

Often, the stability of the motion of a road vehicle is simply addressed as vehicle stability. Vehicle stability inherently deals with the stability of the system composed by the vehicle and the driver (either human or not). In the literature many different expressions are used to address vehicle stability, namely active safety, handling behavior, running safety, running stability, safe running, stability margin, drifting and even “fun-to-drive.”

In academic books [1, 3,4,5,6,7,8,9,10], the road vehicle stability is studied mostly using linearization. Additionally, the driver is hardly introduced in the loop, and, in any case, a linearized vehicle-and-driver system is studied. A comprehensive analysis of the global stability of vehicle-and-driver system has just started [11,12,13,14,15], despite one billion road vehicles run on the streets of the globe.

The generic topic of stability is being dealt with by many authors, (see, e.g., [16,17,18,19,20]). They often study how to cope with vehicle-and-driver instability, without focusing on the ontological problem of what is it exactly vehicle-and-driver stability. The comprehensive and fundamental topic of global stability needs a substantial contribution that this paper aims to start providing.

Abe [5] has given a good early investigation on the stability of the motion of car and driver. The stability was studied referring to a simplified linear vehicle model.

In 1972, Pacejka pioneered the study of stability of nonlinear road vehicle models. He could not exploit all the potentials of Bifurcation Theory, due to limited computer power available at that time. Nonetheless, he showed the existence of multiple equilibria of different type, e.g., stable foci and saddles [7], rising the problem of global stability of a vehicle and fostering further subsequent research in the field.

In 1991, Tousi, Bajaj and Soedel [21] produced an early attempt to study vehicle and driver considering non linear models.

In 1996, Liu, Payre and Bourassa [22] produced another milestone contribution. They highlighted that a vehicle driven by a human may exhibit a number of typical nonlinear behaviors. They used a simple theoretical model (5 state variables, simple driver included), and they did discover even chaos. The paper was theoretical only.

In 2012, some of the authors of this paper [23] produced a complete portrait of nonlinear behaviors of different vehicles with fixed control. Bifurcation theory was exploited. The wealth of different unstable vehicle behaviors depended exclusively on tyre characteristics (not on driver control). A number of different bifurcations were found, namely: homoclinic, heteroclinic, saddle-node, transcritical, Hopf (sub- or super-critical), Korazov-Takens. Again, the paper was theoretical only. Similar but more specific analyses were carried on in [24, 25]. These results can be summarized as follows

• For usual vehicle forward velocities, the bare vehicle is always stable even after strong disturbances, provided it is understeering at any lateral acceleration level, i.e., tyre characteristics are properly chosen (this is accomplished always by carmakers),

• Unstable motion may be generated, without driver’s control, if a certain combination of initial conditions (i.e., disturbances) are applied.

Note that these studies did not take into account the active control by the driver.

To study the stability of the motion of vehicle and driver, an accurate driver model is needed. Unfortunately, we have rough not validated driver models available today [26]. This prevents accurate nonlinear mathematical stability analyses dealing with vehicle and driver. Moreover, driver models have been developed—and are still being developed—to mimic the driver following a given path. Current driver models seem not so efficient to react to a disturbance or to control a drifting vehicle.

Recently, theoretical and experimental research has been undertaken to understand vehicle-and-driver nonlinear behavior. Ploechl and Edelmann [26] studied the drifting (i.e. powerslide) of cars at high lateral acceleration. They demonstrated the existence of highly nonlinear behaviors in the real world.

Since humans seem reluctant to let their behavior be described by deterministic mathematical models [26], driving simulator technology is needed for studying vehicle motion stability [27]. An attempt to find bifurcations with a human driver in the loop was performed in [11]. By using a validated driving simulator, a stable understeering vehicle was considered. The driver was able to make the motion unstable, actually unstable limit cycles were detected. Increasing the forward velocity of the vehicle, the amplitude of such unstable limit cycles did reduce, until a subcritical Hopf bifurcation was reached. Increasing the vehicle forward velocity, after the bifurcation, the motion was chaotic. A doubt existed on whether limit cycles could be reputed as certainly real and whether the knowledge of their existence could be useful in the actual engineering practice. This paper aims to answer these questions.

The accurate mathematical description of the stability of vehicle-and-driver motion is still under development. Nowadays the development of anti-spin controls is performed by a trial-and-error approach: Cars, either virtual or real, are driven on low friction surfaces (e.g., iced lakes during winter time) and, after comprehensive tests, a final judgment is taken on safety. In [28], the first and successful anti-spin controlled systems like ESP were conceived by considering basic phase portraits, fostering new kinds of control systems for anti-spin [29] based on phase portraits and bifurcation analysis.

In the literature, just one contribution has been found to study the stability of the motion of vehicle and driver by deriving a Lyapunov function [30]. The driver was very simple and no experimental activity was performed.

Despite bifurcation theory is being used since some time to study the behavior of vehicles [31], it seems that much effort should be devoted in the future to analyze the dynamic behavior of vehicle and driver. Relevant contribution in this field is being provided in [30, 32] looking at automated vehicles. A comprehensive status of research for connected and automated vehicles is given in [33].

In this study, we first use bifurcation analysis and Lyapunov theory to highlight the stability properties of a vehicle-and-driver model, then we validate our theoretical results experimentally via experiments with a human in the loop. Therefore, while the paper deals principally on human driver control, the results we obtain can be extended also for automated vehicles. There are three important hypotheses that have been assumed for sake of simplicity.

• 1. The path tracking of the driver is rectilinear;

• 2. The forward velocity of the vehicle is constant. We will provide evidence that such an assumption leads to a reasonable accuracy of the results.

• 3. No controls are assumed to act [34], in a future study the effects of controls on global stability of vehicle and driver may be discussed.

The paper is organized as follows. At first, a new simple vehicle-and-driver model that captures reasonably the stability issues, is introduced. Then such a simple model is compared with the corresponding complex vehicle model running on a driving simulator with an actual human driver in the loop. Finally a necessary and sufficient condition is provided to explain the global stability of the motion of vehicle and driver.

2 Vehicle simple model and driver simple model

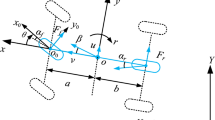
Referring to Fig. 1, the equations of motion can be derived as follows. A moving reference system with origin fixed at the center of gravity G of the vehicle is used. The longitudinal axis x is parallel to the centerline of the vehicle; the vertical axis is perpendicular to the ground and directed towards the ground (not shown in the figure); the lateral axis y is congruent with a right-hand reference system. The degrees of freedom are the lateral motion and the yaw rotation. The longitudinal motion is not considered as a degree of freedom because the forward (longitudinal) velocity u is considered constant. The longitudinal forces, either front ($F_{x_f}$) or rear ($F_{x_r}$), which are needed to keep constant the forward velocity, are considered small. The lateral axle forces, either front ($F_{y_f}$) or rear ($F_{y_r}$) refer to the so-called Axle characteristics [7] and can be modeled by using the well-known Pacejka Magic Formula which was adapted and reads

$$\begin{aligned} F_{y_{i}}&= D_{i}\sin \bigg ( C_{i}\arctan \bigg ( B_{i}\alpha _{i} \nonumber \\&\quad -E_{i}\left( B_{i}\alpha _{i} - \arctan \left( B_{i}\alpha _{i}]\right) \right) \bigg )\bigg ) \end{aligned}$$

(1)

for $i=\{f,r\}$. The total axle lateral force depends on the slip angle $\alpha _i$ ($i=\{f,r\}$) defined as

$$\begin{aligned} \alpha _{f} = \delta - \left( \frac{v + ra}{u} \right) ,\qquad \alpha _{r} = - \left( \frac{v - rb}{u} \right) \end{aligned}$$

(2)

where v is the lateral speed, r the yaw rate, $\delta$ the steering angle, and a and b are the distance of the front and rear axle from the center of mass, respectively(see Fig. 1). The equations of motion of the single-track model can be derived by using D’Alembert’s principle

$$\begin{aligned} {\dot{v}}= & {} \frac{1}{m}\left( F_{y_{f}} + F_{y_{r}} {+F}\right) - ur \end{aligned}$$

(3)

$$\begin{aligned} {\dot{r}}= & {} \frac{1}{J}\left( aF_{y_{f}} - bF_{y_{r}} {+M}\right) , \end{aligned}$$

(4)

where m and J are the vehicle mass and inertia, respectively, and F and M are external generalized forces acting as disturbances, thus, generically, not present. In particular, F is an external force acting at the center of gravity G, orthogonal to the longitudinal axis of the vehicle, and M is a moment orthogonal with respect to the ground.

Fig. 1

Simple mechanical model of a vehicle and driver moving in the horizontal plane. The forces acting at the four wheels are substituted by the resultants acting at the axle centers. The vehicle body, shaded in gray, is simply a rigid body moving in the (X, Y) plane. The rectilinear reference path is depicted in bold and taken, without loss of generality, at $Y=Y_{\text {ref}}$. Parameter values used in the numerical and experimental settings are reported in Appendix A

The driver model is developed according to [26]. The driver controls the steering wheel to place a point P on the reference trajectory, bold in Fig. 1. The steering action is proportional to the path error computed at a certain distance L in front of the vehicle. This distance is proportional to the forward velocity u by setting a fixed preview time $T_{\text {prev}}$, so $L = T_{\text {prev}} u$. The coordinates of the preview point in the global reference system and its speed components can be computed starting from the coordinates of the center of gravity in the global reference system as follows

$$\begin{aligned}&{\textbf{P}} = \left( x_{P} \right) {\textbf{i}}_{{\textbf{0}}} + \left( y_{P} \right) {\textbf{j}}_{{\textbf{0}}} =\left( x_{G} + L\cos \psi \right) {\textbf{i}}_{{\textbf{0}}} \\&\qquad + \left( y_{G} + L\sin \psi \right) {\textbf{j}}_{{\textbf{0}}} \end{aligned}$$

The speed of point P reads

$$\begin{aligned}&{\textbf{V}}_{{\textbf{P}}} = \left( \dot{x}_{P} \right) {\textbf{i}}_{{\textbf{0}}} + \left( \dot{y}_{P} \right) {\textbf{j}}_{{\textbf{0}}} = \left( \dot{x}_{G} - {\dot{\psi }}L\sin \psi \right) {\textbf{i}}_{{\textbf{0}}} \\&\quad \qquad + \left( \dot{y}_{G} + {\dot{\psi }}L\cos \psi \right) {\textbf{j}}_{{\textbf{0}}} \end{aligned}$$

Without loss of generality, we fix the rectilinear desired path parallel to the X axis at $Y_{\text {ref}}=0$. So doing, the path error is

$$\begin{aligned} e = \left( Y_{\text {ref}} - y_{P} \right) = - y_{P} =-y_G -L \sin \psi \end{aligned}$$

(5)

and its derivative reads

$$\begin{aligned} {\dot{e}} = -\dot{y} _G - L r \cos \psi \end{aligned}$$

(6)

The steering angle is applied by the driver with a delay $\tau$

To further simplify the driver model, we now approximate the delayed Eq. $\star$ with a suitable ordinary differential equation. Since the typical driver delay $\tau$ is around 0.2s [1, 4, 26] we can expand the equation ($\star$) in Taylor series around t, obtaining

$$\begin{aligned} \delta (t + \tau ) = \delta (t) + {{\dot{\delta }}}(t) \tau + \frac{1}{2} \ddot{\delta }(t) \tau ^2 + \frac{1}{6} \dddot{\delta }(t) \tau ^3 +\ldots \end{aligned}$$

By applying the Laplace transform to the above equation at both left and right sides, we can compare the following different transfer functions G(s) (s is the Laplace variable)

• Infinite-order Taylor approximation: $G_0(s)=e^{s \tau }$

• First-order Taylor approximation: $G_1(s)=1 + s\tau$

• Second-order Taylor approximation: $G_1(s)=1 + s\tau + \frac{1}{2}{s^{2}\tau }^{2}$

• Third-order Taylor approximation: $G_3(s)=1 + s\tau + \frac{1}{2}{s^{2}\tau }^{2}+ \frac{1}{6}s^{3}\tau ^{3}$

• Fourth-order Taylor approximation: $G_4(s)=1 + s\tau + \frac{1}{2}{s^{2}\tau }^{2}+ \frac{1}{6}s^{3}\tau ^{3}+ \frac{1}{24}s^{4}\tau ^{4}$

• Third-order Padé approximation: $G_5(s)=\frac{{- s}^{3}\tau ^{3} + {{12s}^{2}\tau }^{2} - 60s\tau + 120}{s^{3}\tau ^{3} + {12s^{2}\tau }^{2} + 60s\tau + 120}$

Fig. 2

Comparison of different transfer functions for approximating the delay of the steering action $\delta (t + \tau )$, $\tau = 0.2 {\text {s}}$, as function of the steering angle actuation frequency

The frequency responses of the transfer functions $G_i(s)$ ($i=0,5$) are reported in Fig. 2, in the range $[0-2 {\text {Hz}}]$ of steering angle frequency actuation, the typical range exploited by human drivers. Comparing the different frequency responses, one notices that the error is not acceptable for an expansion of Taylor’s series lower than the third order. Padé approximation is a correct estimate for the modulus of the transfer function (left panel of Fig. 2), but gives the worst approximation of the phase delay. It is well known [35] that approximating the delay via a Taylor expansion changes the stability properties of the system. In particular, by increasing the order of Taylor approximation, the maximum value of the delay $\tau$ reduces. We have found that the third-order Taylor approximation is a good compromise between precision and complexity. Interestingly, we will see that with this approximation a sort of a physical interpretation of the steering action delay is possible (see (12)).

Summarizing, we propose to approximate the delayed steering dynamics $\star$ with

$$\begin{aligned} \delta (t) + {\dot{\delta }}(t)\tau + \frac{1}{2}\ddot{\delta }(t)\tau ^{2} + \frac{1}{6}\dddot{\delta }(t)\tau ^{3} = k e(t) + k_{d}{\dot{e}}(t). \end{aligned}$$

By adding two extra state variables, we write this last third-order ODE as

$$\begin{aligned} {\dot{\delta }}= & {} \delta _1 \end{aligned}$$

(7)

$$\begin{aligned} \dot{\delta _1}= & {} \delta _2 \end{aligned}$$

(8)

$$\begin{aligned} \dot{\delta _2}= & {} \frac{6}{\tau ^3} \left( -\delta \!-\tau \delta _1\!-\frac{\tau ^{2}}{2} \delta _2\! + k e\! + k_{d}{\dot{e}}\right) \end{aligned}$$

(9)

In conclusion, the mathematical model that defines the dynamic behavior of the simple vehicle-and-driver model in Fig. 1 has 7 states, $z=(v,r,\delta _2, \delta _1, \delta ,y_G,\psi )$, governed by Eqs. (3–9) and

$$\begin{aligned} {\dot{y}}_G= & {} v + u \psi \end{aligned}$$

(10)

$$\begin{aligned} {\dot{\psi }}= & {} r \end{aligned}$$

(11)

3 Any vehicle is made unstable by driver action for a sufficiently high forward velocity

According with [5, 11, 12, 21, 22], simple vehicle-and-driver models undergo a Hopf bifurcation at a certain forward velocity. The vehicle may be either oversteering or understeering (for the definition of oversteer or understeer see [1]). The driver model used in [5, 11, 21, 22] referred to the first-order Taylor approximation, as introduced in the previous section. In what follows, we show that also the model referring the third-order Taylor approximation (defined by Eqs. (3–11) displays the same property, i.e., a sufficiently high forward velocity exists for which a Hopf bifurcation occurs at $z=(v,r,\delta _2, \delta _1, \delta ,y_G,\psi )=0$.

Let us linearize the equations of motion (3–11) around $z=0$, obtaining that, for small z,

$$\begin{aligned} {\dot{z}} \simeq J z \end{aligned}$$

with

$$\begin{aligned} J = \left[\begin{array}{ccccccc} - \frac{F_f + F_r}{mu} &{} - \frac{aF_f - bF_r + mu^{2}}{mu} &{} 0 &{} 0 &{} \frac{F_f}{m} &{} 0 &{} 0 \\ - \frac{aF_f - bF_r}{Ju} &{} - \frac{aF_f - bF_r}{Ju} &{} 0 &{} 0 &{} a\frac{F_f}{J} &{} 0 &{} 0 \\ - \frac{6}{\tau ^{3}}k_{d} &{} - \frac{6}{\tau ^{3}}k_{d} L &{} - \frac{3}{\tau } &{} - \frac{6}{\tau ^2} &{} - \frac{6}{\tau ^{3}} &{} - \frac{6}{\tau ^{3}}k &{} -\frac{6 u \left( k T_{prev}+k_d\right) }{\tau ^3} \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} u \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right]\end{aligned}$$

where $F_i=B_{i}C_{i}D_{i}$ for $i=\{f,r\}$. The characteristic polynomial of J reads

$$\begin{aligned}{} & {} \lambda ^{7} + \alpha _{1}\lambda ^{6} + \alpha _{2}\lambda ^{5} + \alpha _{3}\lambda ^{4} + \alpha _{4}\lambda ^{3} \\{} & {} \quad + \alpha _{5}\lambda ^{2} + \alpha _{6}\lambda + \alpha _{7}=0 \end{aligned}$$

with

$$\begin{aligned} \alpha _{1}= & {} \frac{3}{\tau }+\frac{\tau F_f \left( a^2 m+J\right) +\tau F_{r} \left( b^2 m+J\right) }{J m \tau u} \\ \alpha _{2}= & {} \frac{-a m \tau ^2 F_f+b m \tau ^2 F_{r}+6 J m}{J m \tau ^2}\\{} & {} +\frac{3 a^2 m \tau F_f+3 b^2 m \tau F_{r}+3 J \tau F_f+3 J \tau F_{r}}{J m \tau ^2 u}\\{} & {} +\frac{(a+b)^2 F_f F_{r}}{J m u^2} \\ \alpha _{3}= & {} \frac{3 \left( -a m \tau ^2 F_f+b m \tau ^2 F_{r}+2 J m\right) }{J m \tau ^3}\\{} & {} +\frac{3 \left( 2 a^2 m \tau F_f+2 b^2 m \tau F_{r}+2 J \tau F_f+2 J \tau F_{r}\right) }{J m \tau ^3 u}\\{} & {} +\frac{3 (a+b)^2 F_f F_{r}}{J m \tau u^2}\\ \alpha _{4}= & {} \frac{6 \left( F_f \left( \tau (a+b)^2 F_{r}+u \left( u k_d \left( a m u T_{prev}+J\right) +a m (a-\tau u)+J\right) \right) +u F_{r} (b m (b+\tau u)+J)\right) }{J m \tau ^3 u^2}\\ \alpha _{5}= & {} \frac{6 \left( F_f \left( (a+b) F_{r} \left( a+u k_d \left( b+u T_{prev}\right) +b\right) +u^2 \left( a k m u T_{prev}-a m+J k\right) \right) +b m u^2 F_{r}\right) }{J m \tau ^3 u^2} \\ \alpha _{6}= & {} \frac{6 F_f F_r(a + b)\left( bk + k_{d}u + T_{prev}ku \right) }{J m\tau ^{3} u}\\ \alpha _{7}= & {} \frac{6 F_f F_r k(a + b)}{J m\tau ^{3}} \end{aligned}$$

To analyze the stability of $z=0$, we apply the Hurwitz criterion and construct the table

$$\begin{aligned} {\textbf{H}} = \begin{bmatrix} \alpha _{1} &{} \alpha _{3} &{} \alpha _{5} &{} \alpha _{7} &{} 0 &{} 0 &{} 0 \\ 1 &{} \alpha _{2} &{} \alpha _{4} &{} \alpha _{6} &{} 0 &{} 0 &{} 0 \\ 0 &{} \alpha _{1} &{} \alpha _{3} &{} \alpha _{5} &{} \alpha _{7} &{} 0 &{} 0 \\ 0 &{} 1 &{} \alpha _{2} &{} \alpha _{4} &{} \alpha _{6} &{} 0 &{} 0 \\ 0 &{} 0 &{} \alpha _{1} &{} \alpha _{3} &{} \alpha _{5} &{} \alpha _{7} &{} 0 \\ 0 &{} 0 &{} 1 &{} \alpha _{2} &{} \alpha _{4} &{} \alpha _{6} &{} 0 \\ 0 &{} 0 &{} 0 &{} \alpha _{1} &{} \alpha _{3} &{} \alpha _{5} &{} \alpha _{7} \end{bmatrix}.\end{aligned}$$

Asymptotical stability occurs if and only if all the determinants of the leading principal minors of ${\textbf{H}}$ are positive. Therefore, to show that a forward velocity u always exists such that the controlled equilibrium becomes unstable, it is sufficient to show that the Hurwitz criterion is not satisfied for $u\rightarrow \infty$.

The condition on the first principal minor is

$$\begin{aligned} \lim _{u\rightarrow \infty } \alpha _{1} = \frac{3}{\tau } \end{aligned}$$

and is always satisfied. The condition on the second minor is

$$\begin{aligned} \lim _{u\rightarrow \infty } \det \begin{bmatrix} \alpha _{1} &{} \alpha _{3} \\ 1 &{} \alpha _{2} \end{bmatrix} = \lim _{u\rightarrow \infty } \alpha _{1}\alpha _{2} - \alpha _{3} = \frac{12}{\tau ^3}, \end{aligned}$$

is again always satisfied. From the third minor (this and the following expressions are too involved and, therefore, not reported), we find

$$\begin{aligned} \lim _{u\rightarrow \infty } \det \begin{bmatrix} \alpha _{1} &{} \alpha _{3} &{} \alpha _{5} \\ 1 &{} \alpha _{2} &{} \alpha _{4} \\ 0 &{} \alpha _{1} &{} \alpha _{3} \end{bmatrix}> 0 \ \text { iff }\ 3 k_d > k \tau \end{aligned}$$

Fig. 3

A Bifurcation diagram for an oversteering vehicle (OV) (data in Appendix A). Simple vehicle-and-driver model. The projection of the unstable limit cycles on the (v, r) plane as function of vehicle forward velocity u (${\text {km/h}}$) is reported in orange. The limit cycle shrinks on the controlled equilibrium (thick line) changing its stability (green: stable equilibrium, red: unstable equilibrium) at a subcritical Hopf bifurcation (at $u = 122\, {\text {km/h}}$). B and C Projection of the saddle-type limit cycle (black line) onto the $(\psi ,v,r)$ subspace at $u=90~{\text {km/h}}$ (B) and $u=120 \;{\text {km/h}}$ (C). The red surface is the projection on the 3D subspace of the 6D stable manifold of the limit cycle, whose intersection with each plane is reported in blue, while the black closed curve is the projection of the limit cycle on each plane. The closed blue lines on the (v, r) planes are called ISMaVeR (Intersection of the Stable Manifold with the lateral-Velocity/yaw-Rate plane) and define the basin of attraction of the controlled equilibrium when $\psi =y_G=\delta =\delta _1=\delta _2=0$

Looking at the fourth, the fifth, the sixth and the seventh minors, stability is achieved for the opposite condition, i.e. $3 k_d< k \tau$. This means that if u is sufficiently large the equilibrium is unstable.

By inspection of the characteristic polynomial, since $\alpha _7>0$ (independently from u), none of the eigenvalues can be zero. This implies that, as u is increased, the eigenvalues that become unstable cross the imaginary axis not passing through zero, so they are complex conjugate. Thus the bifurcation that causes the stability loss is a Hopf bifurcation.

Fig. 4

A Bifurcation diagram for an understeering vehicle (UN) (data in Appendix A). Simple vehicle-and-driver model. The projection of unstable and stable limit cycles as function of vehicle forward velocity on the (v, r) plane are reported as an orange and green surface, respectively. A Hopf bifurcation occurs at $u = 177\, {\text {km/h}}$, and a limit point of cycle bifurcation occurs at $u = 78\, {\text {km/h}}$. B and C Projection of the unstable limit cycle (black line) onto the $(\psi , v, r)$ subspace at $u = 90~ {\text {km/h}}$ (B) and $u=120 ~{\text {km/h}}$ (C). The red surface is the projection on the 3D subspace of the 6D stable manifold of the limit cycle, whose intersection with each plane is reported in blue (we call the one on the (v, r)-plane ISMaVeR) together with the projection on the plane of the limit cycle, in black

It is important to notice that an understeering vehicle -with fixed steering wheel control- is stable at any forward velocity [1, 3,4,5,6,7,8,9,10], i.e., a limit velocity does not exist at which the vehicle becomes unstable. Here we show that, with driver’s control, this situation is not true.

4 Existence of a saddle-type limit cycle

In Fig. 3A the bifurcation diagram of the simple vehicle-and-driver model referring to an oversteering vehicle is reported (the diagram has been computed using MatCont [36], parameter values are in Appendix A). The system undergoes a Hopf bifurcation as the velocity increases, as expected: it occurs at ($u = 122~{\text {km/h}})$ (where the color of the straight line changes from green to red). The Hopf bifurcation is subcritical: at the bifurcation, a saddle-type limit cycle (its projection on the (v, r) plane is reported in orange) shrinks on the controlled equilibrium, changing its stability. In Fig. 3B and C the limit cycle is projected onto three planes at forward velocity u = 90 km/h and u = 120  km/h (black line in the figure). The limit cycle appears to be saddle-type, thus unstable. A two-dimensional unstable manifold is present together with a six-dimensional stable manifold, and the saddle-type limit cycle is at the intersection of such two manifolds. We computed the intersection of the six-dimensional stable manifold of the saddle-type limit cycle with the iper-surface $\delta =\delta _1=\delta _2=y_G=0$ by selecting the possible initial conditions in the $(v,r,\psi )$-space with a sufficiently fine mesh and looking for the one that converge to the saddle-type limit cycle. The result of this procedure is a surface in the three-dimensional space $(v,r,\psi )$, that we report in red in each panel. The surface delimits the basin of attraction of the desired equilibrium: the points inside the stable manifold converge to the controlled equilibrium, the ones outside the stable manifold diverge or go on another attractor. We consider of particular interest the intersection of the stable manifold on the (v,r) plane. We propose to call it ISMaVeR (Intersection of the Stable Manifold with the lateral-Velocity/yaw-Rate plane). Any disturbance that generates a yaw rate r and a lateral speed v (with $\psi =y_G=\delta =\delta _1=\delta _2=0$) can be identified by a point in the plane v, r. If the point lies inside the ISMaVeR, the motion is stable, if the point lies outside, the motion is unstable. The state variables v and r are important because are related to the linear kinetic energy and to the yaw kinetic energy, as we will detail at the beginning of Sect. 7.

In Fig. 4A the bifurcation diagram of the simple vehicle-and-driver model referring to an understeering vehicle is reported (see parameter values in Appendix A). The system undergoes a Hopf bifurcation as the velocity increase, as expected: it occurs at $u = 177\, {\text {km/h}}$ (where the color of the straight line changes from green to red). The Hopf bifurcation is subcritical: at the bifurcation the equilibrium loses its stability property and a saddle-type limit cycle shrinks on it. The saddle-type limit cycle originates from a limit point of cycle bifurcation at $u = 78\, {\text {km/h}}$. At that bifurcation, it collapse on a stable limit cycle, that exists for higher forward velocity. For smaller velocities, the only possible attractor is the steady state equilibrium, i.e., in this case any reasonable perturbation can be absorbed by the system. Between 78 and 177 km/h the system is bistable, i.e., it can go on the steady state as well on a stable periodic solution. However, this solution, that is present also for higher forward velocity, may have big excursion (in yaw rate, as well as in lateral velocity), so that this stable solution of the model is not realistic.

In Fig. 4B and C the unstable limit cycle is projected onto three planes at forward velocity u = 90  km/h and u = 120 km/h (black lines in the figure). The limit cycle is of saddle-type, with a two-dimensional unstable manifold and a six-dimensional stable manifold. The intersection of the stable manifold of the saddle-type limit cycle with the iper-surface $\delta =\delta _1=\delta _2=y_G=0$ is shown in the $(v,r,\psi )$ three-dimensional space, in red. It delimits the basin of attraction of the controlled equilibrium: the points inside the stable manifold converge to it, the ones outside the stable manifold go on the stable (unrealistic) limit cycle.

5 Driving simulator and complex vehicle model

In order to check whether the theoretical forecasts provided with the simple model in Fig. 1. could be trusted, a driving simulator has been used. Testing unsafe maneuvers in an actual track is very dangerous. Driving simulator technology is nowadays considered quite close to reality [27].

Fig. 5

The driving simulator and the complex car model that were used to validate the results coming from bifurcation analysis of the model in Fig. 1 Data are reported in Appendix A

In a driving simulator, an actual human driver is in the loop with a mathematical model of the vehicle. The driving simulator at Politecnico di Milano, shown in Fig. 5, is a DIM400 manufactured by VI-Grade and is cable driven [37]. The vehicle mathematical model, that we refer as complex model, is a experimentally validated [11, 37] 14 degrees-of-freedom model, whose main configuration data are reported in Appendix A. The complex vehicle model has detailed sub-models of tyres, suspension, steering systems, power-train and bodywork. A complete description of the complex vehicle model can be found in [1, 37] and is not reported here. The parametrization of the simple model in Fig. 1 has been made referring to the complex vehicle model. Such a model has been used in the driving simulator experiments. Both the simple model and the complex model have been tuned to effectively characterize the same vehicle. Fundamental parameters, as the mass properties (mass, location of the center of gravity, inertia tensor) and the tyre characteristics, are the same for the two vehicle models.

Since motion cueing may influence considerably the response of the machine driven by a human [27], no motion cueing (or reduced motion cueing) has been adopted for experiments at the driving simulator. This provides a considerable immersive feeling by the driver [38].

5.1 Disturbance application

At the driving simulator, a disturbed straight running condition is reproduced by applying an external force F and an external moment M acting for a short time $T_d$. The force F acts at the center of gravity G of the vehicle, the moment M is orthogonal with respect to the ground, as presented in Sect. 2 and in Fig. 1. More precisely, we first let the complex vehicle model with human driver run at steady state, i.e., the human driver is driving the simulator at a given forward velocity along a straight line. Then, the external force F and the external moment M are applied according to a time function of the type $1-\cos (2\pi t /T_d)$, with $T_d=0.1\ s$.

In the simple model, if we apply the force $F=m v_0/T_d$ (resp. $M=Jr_0/T_d$) and we let the time $T_d$ tend to zero, we move the system from $z=0$ to a condition in which all the state variables are 0 with the exception of v (resp. r) that takes value $v_0$ (resp. $r_0$). Applying our disturbance to the complex model, since we selected a very small $T_d$, we found v and r at a prescribed value, and we found that the other state variables are very small. In all the experiments we did, we got $|\delta _1|< 1\ {\text {deg}}/ {\text {s}}$, $\delta < 1/20\ {\text {deg}}$, $y_G<10\ {\text {mm}}$ and $\psi < 1\ {\text {deg}}$ just after the disturbance.

Since the reaction time of the driver is much higher than $T_d$ (at least twice) and the driver is not aware of the arrival of the disturbance, the disturbance set the initial conditions of the system at a desired point of the (v, r)-plane in a fully reproducible way. In other words, since the driver has not the time to react, the application of the same external force F and same moment M always leads to the same initial conditions.

6 Validation of the simple vehicle-and-driver model

In this Section, we will try to establish a relationship between the dynamic behavior of the simple system of Fig. 1 and the dynamic behavior of the complex vehicle model controlled by a human driver at the driving simulator. The aim is to allow a quick understanding of the behavior of the vehicle with human driver by resorting to the features of the nonlinear behavior of the simple vehicle-and-driver model. The validation is obviously qualitative since the simple vehicle-and-driver model is too simplified to capture the extremely complex behavior of both the complex vehicle system and the human driver.

6.1 Existence of Hopf bifurcations

First, we look for the existence of Hopf bifurcations like the ones depicted in Figs. 3 and 4 at the driving simulator. To do so, we increased the forward velocity of the vehicle at the driving simulator up to the point the driver is not able to keep the straight path trajectory, without applying any disturbance. The results of this experiment are reported in Table 1.

Table 1 Forward velocities at which the driver at the driving simulator is not capable of running straight ahead. A Hopf bifurcation is thought to occur. Data in Appendix A

Fig. 6

Comparison between the ISMaVeR computed with the simple vehicle-and-driver model and the smallest initial conditions at the driving simulator which cause instability. Dots refer to initial conditions of the complex vehicle model driven -at the driving simulator- by a human driver. The dots are green if the driver can return to the desired path after the disturbance, red otherwise. Top and bottom rows report, respectively, the results for the oversteering (OV) and the understeering (UN) vehicle. Data are reported in Appendix A

6.2 Extent of the domain of attraction

To evaluate the extent of the basin of attraction of the controlled equilibrium (the regions bounded by the ISMaVeR in Figs. 3 and 4), we apply at the driving simulator a disturbance as described in Sect. 5. Then, we measure the obtained initial condition in the (v, r) plane, and we evaluate if the human driver is capable to get back to the initial straight trajectory. The results of this experiment, together with the ISMaVeR predicted by the simple vehicle-and-driver model, are reported in Fig. 6. We repeated the experiment at two different velocities, for the oversteering configuration at $65\ {\text {km/h}}$ (Fig. 6A) and $90\ {\text {km/h}}$ (Fig. 6B), while for the understeering configuration at $90\ {\text {km/h}}$ (Fig. 6C) and $126\ {\text {km/h}}$ (Fig. 6D). A reasonable agreement is found between the results predicted by the simple vehicle-and-driver model and the corresponding results obtaining at the driving simulator. The main differences can be traced back to the rollover motion, that is modeled in the complex model only.

Fig. 7

Projection of two trajectories in the $(v-r)$–plane departing in the neighborhood of the ISMaVeR, obtained with the complex vehicle model controlled by a human driver at the driving simulator (top panels) and with the simple vehicle-and-driver model (bottom panels) for the oversteering (left panels) and the understeering (right panels) vehicle configuration. Forward speed $u=90\ {\text {km/h}}$. Data are reported in Appendix A

6.3 Existence of a saddle-type limit cycle

Finally, we tried to detect the existence of a limit cycle. Obviously, the existence of an unstable limit cycle can be detected in an approximated way only. However, being of saddle type, it is possible to detect it by looking for an initial condition that is in the neighborhood of the stable manifold. In fact, initial conditions outside but near to the ISMaVeR should produce a motion that evolves towards the saddle-type limit cycle and then diverges, while conditions inside the ISMaVeR produce a motion that evolves towards the limit cycle and then to the controlled trajectory $z=0$. We therefore calibrated the disturbance in order to get these two initial conditions (very close each other) for the complex vehicle model controlled by a human driver at the driving simulator: Fig. 7 reports the projection of the obtained trajectories on the (v, r)–plane both for the oversteering vehicle (panel (A)) and the for the understeering vehicle (panel (B)). The forward velocity u is kept at $90\ {\text {km/h}}$ as far at it is possible (even when the motion becomes unstable). In the bottom panels, we report the corresponding trajectories obtained with the simple vehicle-and-driver model. Again, a good qualitative correspondence is found.

7 Computation of the domain of attraction of the controlled trajectory

A Lyapunov function is now introduced for the simple vehicle-and-driver model. Lyapunov functions can be used to define the exact region of asymptotic stability (domain of attraction) of a specific equilibrium in a nonlinear system [39,40,41] by Zubov’s methods. Following the procedure proposed in [41], we select the Lyapunov function V by first defining its first derivative ${\dot{V}}$.

${\dot{V}}$ is defined as minus the variation of the kinetic energy $E_k$ of the vehicle plus the energy associated to the steering action $E_s$

$$\begin{aligned} {\dot{V}} = -\left( \Delta E_k + E_s\right) . \end{aligned}$$

The variation of the kinetic energy is due to the lateral motion of the vehicle which runs at a constant forward velocity. Let us name $E_k(t)$ the kinetic energy at the time t and $E_k(\infty )$ the kinetic energy at steady state. By means of the König’s theorem [42], such a variation is composed by two terms, namely, the kinetic energy associated to the vehicle velocity $\sqrt{v^2+u^2}$ (composed by the two orthogonal vectors v and u) and the kinetic energy associated to yaw rate r. Therefore

$$\begin{aligned} \Delta E_k(t)= & {} E_{k}(t) - E_{k}(0) \\= & {} \left( E_{k}(t) - E_{k}(0) \right) _{\text {linear}} + \left( E_{k}(t) - E_{k}(0) \right) _{\text {rotational}} \\= & {} \frac{1}{2}m\left( u^{2}(t) + v^{2}(t) - u^{2}(0) -v^{2}(0) \right) \\{} & {} + \frac{1}{2}J\left( r^{2}(t) - r^{2}(0) \right) . \end{aligned}$$

Considering that at $t=0$ we are at steady state, $v(0)=r(0)=0$, and that the forward velocity is kept constant, so $u(0)=u(t)=u,\ \forall t$, we finally obtain

$$\begin{aligned} \Delta E_k(t) = \frac{1}{2}mv^{2}(t) + \frac{1}{2}Jr^{2}(t). \end{aligned}$$

The energy associated to the steering action $E_s$ can be computed as

$$\begin{aligned} E_s = \int _{0}^{\delta }{\xi \tau }^{2}\ddot{\delta } {\text {d}}\delta + \int _{0}^{\delta } \xi \tau {\dot{\delta }} {\text {d}}\delta + \int _{0}^{\delta }\xi \delta {\text {d}}\delta \end{aligned}$$

(12)

where $\xi \delta (t)$ represents an elastic torque, internal with respect to the mechanical model in Fig.1, the rotational stiffness is $\xi = 1\ [ {\text {Nm}}/ {\text {rad}}]$, $\xi \tau {\dot{\delta }}(t)$ represents a viscous torque whose viscous parameter is $\xi \tau \ [{\text {Nms}}/ {\text {rad}}]$, and ${\xi \tau }^{2}\ddot{\delta }(t)$ represents an inertial torque whose rotational inertial parameter is $\xi \tau ^{2}\ [{\text {Nms}}^{2}/ {\text {rad}}]= [{\text {kgm}}^{2}]$.

We have verified in our experiments that $E_s\ll \Delta E_k$ (by several orders of magnitude), thus

$$\begin{aligned} {\dot{V}} \sim - \left( \frac{1}{2}mv^{2} + \frac{1}{2}Jr^{2} \right) \end{aligned}$$

(13)

Note now that the variation of the kinetic energy is equal to the work of all active forces acting on the system, i.e.

$$\begin{aligned} \Delta E_{k}&= \int _0^{y_{f}} F_{y_f} {\text {d}} y_{f} + \int _0^{y_{r}} F_{y_r} {\text {d}} y_r \nonumber \\&\quad +\int _0^x mvr {\text {d}}x+ \int _{0}^{y_{G}} F {\text {d}}y_{G} + \int _{0}^{\psi } M {\text {d}}\psi \end{aligned}$$

(14)

where we used the symbols reported in Fig. 1 and, in particular

• $F_{y_f}$ and $F_{y_r}$ are the lateral axle forces acting at tyres, front or rear, respectively, while $y_f$ and $y_r$ are the corresponding displacements along the directions of the forces. They can be computed as $\int _0^{t} F_{y_i} v_{i} {\text {d}}t$, $i=\{f,r\}$, where $v_f=v+ra$ and $v_r=v-rb$.

• The energy term $\int _0^x mvr {\text {d}}x$ refers to an inertial force acting along the longitudinal axis x of the non-inertial local coordinate system that we have used, see Fig. 1. It can be computed as $\int _0^x mvr {\text {d}}x = \int _0^t mvr\ u {\text {d}}t$ and is needed to keep the forward velocity u constant. Please notice that $mvr=F_{x_f} + F_{x_r}$. This energy is given by the work of the longitudinal forces at the tyres $F_{x_f}$ and $F_{x_r}$, i.e.:

  $$\begin{aligned} \int _0^{x_{f}} F_{x_f} {\text {d}} x_{f} + \int _0^{x_{r}} F_{x_r} {\text {d}} x_r =\int _0^x mvr {\text {d}}x. \end{aligned}$$

• F and M are the external disturbances that we have applied to reach the desired initial conditions, as described in Sect. 5. Note that $\int _{0}^{y_{G}} F {\text {d}}y_{G} = \int _{0}^{T_d} F v {\text {d}}t$, and $\int _{0}^{\psi } M {\text {d}}\psi = \int _{0}^{T_d} M r {\text {d}}t$.

The variation of the kinetic energy, therefore, contains information on all of the acting forces and all of the state variables, and is thus a meaningful quantity.

According to the Lyapunov criterion, a necessary and sufficient condition for asymptotic stability is that a positive function $V(z)>0$ exists such that it vanishes at the equilibrium $z_0$ with negative time-derivative ${\dot{V}}(z)<0,\ \forall z\in \Omega \ne z_0$, where $\Omega$ is an open set that contains $z_0$. Moreover, if ${\dot{V}}(z)>0,\ \forall z\not \in \Omega$ then $\Omega$ is the basin of attraction of the equilibrium $z_0$. Our choice of ${\dot{V}}$ (Eq. (13)) is negative if v and r are not 0. Since the unique equilibrium of model (3–11) with $v=r=0$ is $z=0$, it fulfills the Lyapunov’s requirement. To compute the Lyapunov function for a generic point z(0) of the state space we can therefore use the Fundamental Theorem of calculus as

$$\begin{aligned} V(z({\bar{t}}))-V(z(0)) = \int _0^{{\bar{t}}} \dot{V}(z(t)) {\text {d}}t. \end{aligned}$$

If z(0) belongs to the basin of attraction of $z=0$, then $\lim _{t\rightarrow \infty } z(t)=0$, so we can take ${\bar{t}}$ sufficiently large so that $V(z({\bar{t}}))\sim 0$. As a result

$$\begin{aligned} V(z(0)) = - \int _0^{{\bar{t}}} \dot{V}(z(t)) {\text {d}}t >0 \end{aligned}$$

since $\dot{V}(z)<0, \ \forall z$. On the contrary, if z(0) is outside the basin of attraction of $z=0$, $V(z(t))\rightarrow \infty$ as t increases, thus V(z(0)) can be defined as any negative function. As a result, by applying the Lyapunov criterion, the exact basin of attraction of $z=0$ (in particular, the ISMaVeR) can be estimated with this Lyapunov function. This suggests a necessary and sufficient condition for the stability of the vehicle-and-driver system, which states:

In a vehicle-and-driver system, an initial disturbance is controlled if and only if the variation of kinetic energy (13) goes to zero along the trajectory, i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty } \Delta E_k(t) = \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0. \end{aligned}$$

A formal proof of the condition is reported in Appendix B.

This condition has a twofold practical utility:

• Studying the stability of a vehicle and driver by the system model in Fig. 1 can be made referring to two main state variables only, namely v and r. The comparison of the performance of different control systems can be made in the (v, r)-plane, as anticipated by Horiuchi [25].

• Monitoring the decay of the value of the kinetic energy might be useful to assess whether the vehicle-and-driver approaches a stable motion. Practically the fact that the decay is rather slow, or, in the worst case, oscillatory, is a useful for advanced control algorithms based on Artificial Intelligence, see e.g. [20].

7.1 Validation of the necessary and sufficient condition for stability of vehicle-and-driver systems

A theoretical extension of this last theorem to the more complex vehicle model, driven by a human is practically unfeasible. Actually, to compute the total energy belonging to the vehicle we should consider not only the kinetic energy but also the potential energy related to mass level and elastic elements, as well as the presence of dissipating components like dampers. We therefore checked at the driving simulator whether the necessary and sufficient condition derived in the preceding section holds true, in an engineering sense. Figure 8 reports the evolution of the variation of kinetic energy $\Delta E_k(t)$ in four experiments in the driving simulator. As expected, independently from the fact that the considered vehicle is oversteering (panel (A)) or understeering (panel (B)), the variation of kinetic energy vanishes if the driver is able to control the vehicle (green lines) while diverges if the driver loses the vehicle control.

Fig. 8

Evolution of the variation of kinetic energy $\Delta E_k(t)$ of the complex vehicle driven by a human in controlled (green) and uncontrolled (red) maneuvers. At time $t=0$ the disturbance described in Sect. 5 is applied. (OV/UN: oversteering/understeering configuration). Data are reported in Appendix A

7.2 A note on the role of energy associated to the drivers’ action

The variation of kinetic energy of the vehicle plays a fundamental role on asymptotic stability. As we already stated, referring to the simple vehicle-and-driver model, at the end of the disturbance, the total energy of the vehicle-and-driver system is substantially the variation of the kinetic energy of the vehicle. Such an energy must be dissipated for the system to be asymptotically stable and it cannot be dissipated by the driver, but only by tyres. The driver’s control is therefore just devoted to let tyres dissipate the kinetic energy of the disturbance. On the other hand, the energy that is used to make the vehicle-and-driver system unstable is taken, by the drivers’ action, from the forward motion, precisely during the lateral motions. Looking at Eq. (14), the increase of kinetic energy in the unstable case is essentially due to the inertial force acting along the longitudinal axis $\int _0^x mvr {\text {d}}x$,as correctly assessed by Edelmann and Ploechl [43]. No relevant potential energy is “stored” by the driver, as can be assessed both considering our experiments and by inspection of the terms of Eq. (12).

8 Discussion and conclusion

The aim of the paper was to suggest a basic theory for understanding how drivers lose control of road vehicles after a disturbance has acted. Two vehicle-and-driver systems have been considered to study the global stability of the motion of road vehicles driven by humans.

The first vehicle-and-driver system is composed by a simple vehicle nonlinear model and by a simple driver model. To obtain a simple model, the delay of the steering response by the driver has been modeled by a Taylor series expansion up to the third order. Using this model, we present two main results in terms of mathematical proofs.

The first result is that the controlled trajectory by the vehicle-and-driver model may become unstable independently from the characteristics of the car, either oversteering or understeering, by undergoing a Hopf bifurcation (at a certain forward velocity). To substantiate this result we presented two examples, referring either to an oversteering car or to an understeering car, in which we found two subcritical Hopf bifurcations. We cannot exclude that stability is lost due to supercritical Hopf bifurcations, even if we have not experienced such a bifurcation in our research. In our cases, at the Hopf bifurcation a saddle-type limit cycle occurs, whose six-dimensional stable manifold delimits the basin of attraction of the controlled trajectory.

The second result is a necessary and sufficient condition for which a given disturbance can be rejected or not by the vehicle-and-driver system. In particular, the disturbance is rejected if and only if the variation of the kinetic energy of the vehicle should eventually vanish. This result allows one to to focus on lateral speed and yaw rate if stability has to be studied.

The second vehicle-and-driver system is composed by a complex vehicle model and by a real human driver, controlling the vehicle model at a dynamic driving simulator. The nonlinear dynamic behavior of the simple vehicle-and-driver model has been compared with the behavior of the corresponding complex vehicle model controlled by the human driver at the driving simulator, obtaining a good qualitative agreement. In particular, the Hopf bifurcations featured by the simple vehicle-and-driver model were found at the driving simulator, too. The saddle-type limit cycle featured by the simple vehicle-and-driver model was found at the driving simulator too. The extent of the domain of attraction referring to the simple vehicle-and-driver model is comparable with the corresponding domain of attraction of the complex vehicle driven by a human. As a result, we can say that the assumption that a simple vehicle-and-driver model can provide a qualitative explanation of the dynamic behavior of the complex vehicle model controlled by a real human driver is validated, and therefore we now have new keys for the interpretation of the dynamics of the complex vehicle model and human driver. Without exploiting the simple vehicle-and-driver model, the understanding of the behavior of the complex vehicle model controlled by a human would have been hardly achieved.

The research has clarified that a domain of attraction may exist that depends on both the vehicle parameters and driver parameters. The main restriction is that the tracked path is rectilinear. Future researcher will have to be extended to curved path or transient (lane change) maneuvers.

Although the driving simulator technology is often reputed rather fair in representing extreme maneuvers, further experiments on track are needed for an ultimate validation of the results of this research. Assuming that the experiments at the driving simulator can be trusted, the following conclusions may be drawn for real road vehicles driven by real humans.

There is a domain of attraction for any combination of vehicle and driver. The domain of attraction shrinks with increasing vehicle forward velocity. The amplitude of the domain of attraction is related to at least one limit cycle. The problem of estimating such a domain of attraction becomes crucial for any vehicle either conventional or automated. This estimation will be the topic of future research work. Non-human drivers (automated vehicles) might also be addressed by our research provided that their behavior can be modeled as that of a human. In particular, the presence of delays is common both to humans and automated vehicles, and the order of magnitude of the two delays is similar, even if their nature is different [44]. The delay of a human refer both to cognitive process and actuation of the mechanical action through neurons and muscles. The delay of an automated vehicle refers to the sense-plan-act scheme [45, 46] and is due to the time needed for measurement of physical phenomena, computing for control action, and actuate one or more devices.

Appendices

Appendix A: Models’ parameters

Vehicle
Mass m	1938 ${\text {kg}}$
Inertia J	4063 ${\text {kg m}}^2$
a	1.444 ${\text {m}}$
b	1.529 ${\text {m}}$

Oversteering configuration
Tyres				Driver
$B_f$	14.5 ${\text {rad}}^{-1}$	$B_r$	13.5 ${\text {rad}}^{-1}$	$\tau$	0.2 ${\text {s}}$
$C_f$	1.89	$C_r$	1.45	k	0.025
$E_f$	0.29	$E_r$	0.31	$k_d$	0.004
$D_f$	9778 ${\text {N}}$	$D_r$	9234 ${\text {N}}$	$T_{ {\text {prev}}}$	0.5 ${\text {s}}$

Understeering configuration
Tyres				Driver
$B_f$	9.86 ${\text {rad}}^{-1}$	$B_r$	18.75 ${\text {rad}}^{-1}$	$\tau$	0.2 ${\text {s}}$
$C_f$	1.87	$C_r$	1.53	${\text {k}}$	0.01
$E_f$	0.28	$E_r$	0.30	$k_d$	0.008
$D_f$	9778 ${\text {N}}$	$D_r$	9234 ${\text {N}}$	$T_{ {\text {prev}}}$	0.5 ${\text {s}}$

Appendix B: Necessary and sufficient condition for global stability of vehicle and driver

In this Appendix, we give a proof of the theorem proposed in Sect. 7 that can be formally presented as:

Given the vehicle-and-driver model shown in Fig. 1and described by Eqs. (3–11), where tyre forces are not vanishing, mass properties and vehicle geometry correspond to those of standard vehicles (i.e., limit cases like $F_{x_f}=0$ of $J=0$ are excluded), the necessary and sufficient condition for the vehicle-and-driver system to be asymptotically stable is

$$\begin{aligned} \lim _{t\rightarrow \infty } \Delta E_k(t) =\frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0. \end{aligned}$$

The condition is necessary. Let us make the hypothesis that the system is stable and show that

$$\begin{aligned} \lim _{t\rightarrow \infty } \Delta E_k(t) =\frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0. \end{aligned}$$

Since, for the asymptotic stability hypothesis we have

$$\begin{aligned} \lim _{t\rightarrow \infty } z(t) = \lim _{t\rightarrow \infty } [v,r,\delta _2,\delta _1,\delta ,y_G,\psi ] = 0 \end{aligned}$$

and, in particular

$$\begin{aligned} \lim _{t\rightarrow \infty } v(t) = \lim _{t\rightarrow \infty } r(t) = 0 \end{aligned}$$

thus

$$\begin{aligned} \lim _{t\rightarrow \infty } \Delta E_k(t) = \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0. \end{aligned}$$

The condition is sufficient. Let us make the hypothesis

$$\begin{aligned} \lim _{t\rightarrow \infty } \Delta E_k(t) = \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0 \end{aligned}$$

and show that the system, is stable. First we choose

$$\begin{aligned} \dot{V} = - \left( \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2}\right) . \end{aligned}$$

Given that the region of asymptotic stability is around the origin, by definition

$$\begin{aligned} V(z(t))-V(z(0)) = \int _0^{t} \dot{V}(z(t)) {\text {d}}t. \end{aligned}$$

If z(t) converges to $z=0$, then

$$\begin{aligned} \lim _{t\rightarrow \infty } z(t)=0, \end{aligned}$$

so

$$\begin{aligned} V(z(0)) = - \int _0^{\infty } \dot{V}(z(t)) {\text {d}}t. \end{aligned}$$

Thus, the Lyapunov function for a generic point z(t) is

$$\begin{aligned} V(z(t)) =&\int _0^{t} \dot{V}(z(t)) {\text {d}}||t +V(z(0)) \\ =&\int _0^{t} \dot{V}(z(t)) {\text {d}}t - \int _0^{\infty } \dot{V}(z(t)) {\text {d}}t. \end{aligned}$$

Now, $V(z(t))>0$, since $\int _0^{t} \dot{V}(z(t)) {\text {d}}t > \int _0^{\infty } \dot{V}(z(t)) {\text {d}}t$, being $\dot{V}(z)<0\;\forall z$. Moreover, $V(z(t))=0$ only if $z(t)=0$, so the system is stable for the Lyapunov theorem. Finally, if z(t) does not converge to $z=0$, then

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} \ne 0 \end{aligned}$$

or

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{2}mv(t)^{2} + \frac{1}{2}Jr(t)^{2} = 0 \end{aligned}$$

but with unacceptable conditions. In fact, the only equilibria of system (3–11) with $v=r=0$ different from 0 have $\psi =\pi$ (the vehicle is running with the rear pointing ahead), or $\psi =2\pi$ (the vehicle has undergone a full spin). In the other conditions, Eq. (5) does not vanish, so that $\delta \ne 0$. Note that running with $y_G \ne 0$ with $\delta \ne 0$ are excluded since such condition can be reached if tyre forces are null which has been excluded by hypothesis.