1 Introduction

Nonlinear bridge aerodynamics is an active research field due to the inherent nonlinear behaviour of bluff bridge decks. The progression of experimental methods, numerical methods, and computer power has opened the opportunity to widen the scope beyond linear models. The nonlinear flutter instabilities have been modelled by [1,2,3,4,5]. In References [6, 7] modelled nonlinear galloping, while [8, 9] modelled nonlinear vortex-induced vibrations. Significant contributions to general nonlinear models for bridge aerodynamics have also been made [7, 10,11,12,13,14,15,16,17,18,19]. Modelling and understanding nonlinear bridge behaviour remains a challenging task.

A general type of nonlinear load model is the Volterra Series-based model, initially proposed by Volterra [20]. The Volterra series model extends linear convolutions to higher-order convolutions [21]. Volterra models have been widely used, and the properties of the model have been extensively explored. For a review of Volterra models in an engineering context, see Cheng [22]. Volterra models have also been used in bridge aerodynamics by multiple authors [19, 23,24,25,26,27,28,29,30,31]. The optimal experimental design and identification of Volterra models for bridge aerodynamics is, however, still an open question.

Data-driven identification of Volterra-models was first explored by Wiener [32], who suggested rewriting the Volterra series to the Wiener series via orthogonal Wiener kernels. The Wiener series is made orthogonal using Gram–Schmidt orthogonalisation, assuming Gaussian white noise input as the training data. This method was expanded further by Lee and Schetzen [33], who utilised a cross-correlation-based identification method, where the input data were restricted to Gaussian white noise. Korenberg and Hunter [34] developed an identification method softening the requirements of the input data to Gaussian coloured noise. Amorocho and Brandstetter [35] re-casted the data-driven identification problem to a linear least-squares regression problem. To solve the least-square regression more efficiently, Korenberg [36] proposed the ordinary orthogonal algorithm and the fast-orthogonal algorithm. A significant advantage of the linear least-square regression method is that it does not restrict the form or distribution of the input and output data; for instance, it is not required that the input be Gaussian white noise. However, one of the significant drawbacks of least-squares is potential overfitting. Overfitting is a well-known issue in model identification problems, where it is usually necessary to accept a trade-off between the model complexity and the closeness-of-fit to the dataset output. For Volterra series models, overfitting leads to noise magnification and non-smooth kernel shapes, which is deemed to be an unphysical representation of the fluid memory effects. Nowak [37] addressed removing noise from the kernels by introducing penalties on the kernel’s shapes via regularizing techniques. This idea was further developed by Birpoutsoukis et al. [38, 39], who used decay and smoothing types of regularisation of the kernels up to the 3rd-order. Regularizing the least-squares problem is a widely used technique to reduce the effect of noise and unexplained components in the measured output; thus, they are popular in machine learning applications, as well as inverse problems [40,41,42,43,44]. However, this technique has not yet been explored in the context of Volterra models for bridge aerodynamics.

In this paper, traditional 0th- and 2nd-order Tikhonov regularisation [45] is introduced into the identification of Volterra-kernels. Furthermore, decay-type regularisation is introduced, which is appropriate for systems with finite memory. It is shown that regularisation can reduce the effect of noise and reduce overfitting, which makes the trained models more robust for new predictions. The methods are then tested on a numerical example and on experimental data from one- and two-degrees-of-freedom forced vibration section model tests of a twin deck.

The Volterra models and regularisation techniques are presented in Sect. 1 and 2. In Sect. 3, the methods are explored in a numerical example, while in Sect. 4, the methods are used on experimental data for a twin deck. The final chapter summarises and concludes the findings.

2 Theory

2.1 Data-driven identification in bridge aerodynamics

Training mathematical models for estimating the system behaviour based on input–output data is called data-driven identification. Experimental data in an aerodynamic bridge setting are typically obtained via forced or free vibration wind tunnel tests [46,47,48] or computational fluid dynamics [49,50,51,52]. Figure 1 shows the bridge cross-section considered in this article at the model scale. The forces and moments F and the motions r are also shown, which are referred to as the centre point in the gap. Data from forced vibration tests conducted at the fluid mechanics laboratory at the Norwegian University of Science and Technology are used to fit and validate the Volterra models considered in this paper. Section 4 explains the experimental setup, and more details of the wind tunnel and the forced vibration apparatus are presented in Siedziako et al. [53].

Fig. 1
figure 1

Bridge section considered in this paper and the positive directions of forces and motions. All dimensions are given in mm

Full size image

2.2 Volterra series

In the following, the main equations for discrete Volterra models are presented. A pth-order discrete-time single-input-single-output (SISO) Volterra system with memory length M can be formulated as follows [54]:

$$ F[n] = h_{0} + \sum\limits_{k = 0}^{M} {h_{1} } [k]r[n - k] + \sum\limits_{P = 2}^{p} {H_{M}^{P} [n]} $$
(1)
$$ H_{M}^{P} [n] = \sum\limits_{{k_{1} }}^{M} {...\sum\limits_{{k_{p} }}^{M} {h_{p} [k_{1} ,...,k_{p} ]r[n - k_{1} ]...r[n - k_{p} ]} } $$
(2)

where hp is the pth-order Volterra kernel, r (bridge motion) is the system input, and F is the output (forces). The model can then be expanded to include multiple inputs with the inclusion of cross-kernels, as shown below. A discrete-time 2nd-order Volterra model with two inputs, rz and rθ, can be formulated as follows:

$$ F[n] = h_{0} + \sum\limits_{k = 0}^{M} {h_{1}^{z} } [k]r_{z} [n - k] + \sum\limits_{k = 0}^{M} {h_{1}^{\theta } } [k]r_{1} [n - k] + ... $$
(3)
$$ \sum\limits_{{k_{1} = 0}}^{M} {\sum\limits_{{k_{2} = 0}}^{M} {h_{2}^{z\theta } } } [k_{1} ,k_{2} ]r_{z} [n - k_{1} ]r_{\theta } [n - k_{2} ] + \sum\limits_{{k_{1} = 0}}^{M} {\sum\limits_{{k_{2} = 0}}^{M} {h_{2}^{\theta z} } } [k_{1} ,k_{2} ]r_{\theta } [n - k_{1} ]r_{z} [n - k_{2} ] + ... $$
$$ \sum\limits_{{k_{1} = 0}}^{M} {\sum\limits_{{k_{2} = 0}}^{M} {h_{2}^{zz} } } [k_{1} ,k_{2} ]r_{z} [n - k_{1} ]r_{z} [n - k_{2} ] + \sum\limits_{{k_{1} = 0}}^{M} {\sum\limits_{{k_{2} = 0}}^{M} {h_{2}^{\theta \theta } } } [k_{1} ,k_{2} ]r_{\theta } [n - k_{1} ]r_{\theta } [n - k_{2} ] $$

where \(h_{2}^{zz} \left[ {k_{1} ,k_{2} } \right]\) and \(h_{2}^{\theta \theta } \left[ {k_{1} ,k_{2} } \right]\) denote the 2nd-order direct kernels, while \(h_{2}^{z\theta } \left[ {k_{1} ,k_{2} } \right]\) and \(h_{2}^{\theta z} \left[ {k_{1} ,k_{2} } \right]\) are the 2nd-order cross-kernels. The system in Eq. (3) is referred to as a 2nd-order multi-input–single-output (MISO) system. The equations are only shown for the 2nd-order Volterra system for brevity, but the equations can readily be extended for systems with a higher order. The slightly longer equations involved for a third-order system are shown in "Appendix A". Orders higher than 3 are rarely considered in engineering problems due to the immense computational demand.

2.3 Identification using linear least-squares

Multiple identification techniques exist for identifying Volterra models from input–output data. One of the most popular is linear least-squares [24, 55]. A significant advantage of least-squares identification is that there is no restriction on the type of motion used for the input data. However, it should be noted that, although no assumptions on the input are made, it is still vital to use inputs that are as similar to the predictive situations the models are to be used on, considering the reduced frequency, motion histories and motion amplitudes. Considering a dataset with N input–output triplets (two inputs and one output), the system model can be written as follows:

$$ {\textbf{F}}_{N \times 1} = {\textbf{r}}_{N \times Q} {\textbf{H}}_{Q \times 1} $$
(4)

where F is the system output vector, r is the system regression matrix, And H is a vector that contains all Q unknown parameters (i.e., the Volterra kernel coefficients), as shown later in this chapter. The subscript \(a \times b\) denotes the number of rows and columns, and is omitted where dimensions are obvious. In most data-driven identifications, the number of equations N is larger than the number of unknown variables Q, making the system overdetermined, and thus with no unique solution. However, a standard approximate solution is found with the linear least-squares method that aims to minimise the second norm of the system residual:

$$ \arg \min _{{\textbf{H}}} \left( {\left\| {{\textbf{F}} - {\mathbf{rH}}} \right\|_{2}^{2} } \right) $$
(5)

The output vector is given by

$$ {\textbf{F}}_{N \times 1} = [F[0],F[1],...,F[N]]^{T} $$
(6)

where F is the output. For the 2nd-order Volterra model case, the regression matrix is constructed in the following way:

$$ {\textbf{r}}_{N \times Q} = [{\textbf{r}}_{{z,N \times Q_{1} }}^{{}} ,{\textbf{r}}_{{\theta ,N \times Q_{1} }}^{{}} ,{\textbf{r}}_{{zz,N \times Q_{2} }}^{{}} ,{\textbf{r}}_{{\theta \theta ,N \times Q_{2} }}^{{}} ,{\textbf{r}}_{{z\theta ,N \times Q_{2} }}^{{}} ,{\textbf{r}}_{{\theta z,N \times Q_{2} }}^{{}} ] $$
(7)

where rz and rθ are the two inputs of the system. The submatrices in the regression matrix in Eq. (7) can be constructed as follows:

$$ {\textbf{r}}_{{z,N \times Q_{1} }}^{{}} = \left[ {\begin{array}{*{20}c} {r_{z} [0]} & 0 & \cdots & 0 \\ {r_{z} [1]} & {r_{z} [0]} & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ {r_{z} [N]} & {r_{z} [N - 1]} & \cdots & {r_{z} [N - M]} \\ \end{array} } \right] $$
(8)

The structure for \({\textbf{r}}_{{\theta ,N \times Q_{1} }}^{{}}\) is similar. The contributions for the second-order direct and cross-terms can be constructed in the following fashion:

$$ {\textbf{r}}_{{zz,N \times Q_{2} }}^{{}} = \left[ {\begin{array}{*{20}c} {r_{z} [0]^{2} } & {r_{z} [0]0} & \cdots & {r_{z} [0]0} \\ {r_{z} [1]^{2} } & {r_{z} [1]r_{z} [0]} & \cdots & {r_{z} [1]0} \\ \vdots & \vdots & \vdots & \vdots \\ {r_{z} [N]^{2} } & {r_{z} [N]r_{z} [N - 1]} & \cdots & {r_{z} [N]r_{z} [N - M]} \\ \end{array} \ldots \begin{array}{*{20}c} {r_{z} [0 - M]r_{z} [0]} & {r_{z} [0 - M]0} & \ldots & {r_{z} [0 - M]0} \\ {r_{z} [1 - M]r_{z} [1]} & {r_{z} [1 - M]r_{z} [0]} & \ldots & {r_{z} [1 - M]0} \\ \vdots & \vdots & \vdots & \vdots \\ {r_{z} [N - M]r_{z} [N]} & {r_{z} [N - M]r_{z} [N - 1]} & \cdots & {r_{z} [N - M]^{2} } \\ \end{array} } \right] $$
(9)
$$ {\textbf{r}}_{{z\theta ,N \times Q_{2} }}^{{}} = \left[ {\begin{array}{*{20}c} {r_{z} [0]r_{\theta } [0]} & {r_{z} [0]0} & \cdots & {r_{z} [0]0} \\ {r_{z} [1]r_{\theta } [1]} & {r_{z} [1]r_{\theta } [0]} & \cdots & {r_{z} [1]0} \\ \vdots & \vdots & \vdots & \vdots \\ {r_{z} [N]r_{\theta } [N]} & {r_{z} [N]r_{\theta } [N - 1]} & \cdots & {r_{z} [N]r_{\theta } [N - M]} \\ \end{array} \ldots \begin{array}{*{20}c} {r_{z} [0 - M]r_{\theta } [0]} & {r_{z} [0 - M]0} & \ldots & {r_{z} [0 - M]0} \\ {r_{z} [1 - M]r_{\theta } [1]} & {r_{z} [1 - M]r_{\theta } [0]} & \ldots & {r_{z} [1 - M]0} \\ \vdots & \vdots & \vdots & \vdots \\ {r_{z} [N - M]r_{\theta } [N]} & {r_{z} [N - M]r_{\theta } [N - 1]} & \cdots & {r_{z} [N - M]r_{\theta } [N - M]} \\ \end{array} } \right] $$
(10)

Although not shown here, matrices \({\textbf{r}}_{\theta \theta }^{{}}\) and \({\textbf{r}}_{\theta z}^{{}}\) are similarly constructed by changing the subscripts. The unknown parameter vector to be determined is defined as:

$$ {\textbf{H}}_{Q \times 1} = \left[ {{{\textbf{H}}_{{Q_{1} \times 1}}^{z}}^T ,{{\textbf{H}}_{{Q_{1} \times 1}}^{\theta}}^{T} ,{{\textbf{H}}_{{Q_{2} \times 1}}^{zz}}^{T} ,{{\textbf{H}}_{{Q_{2} \times 1}}^{\theta \theta}}^{T} ,{{\textbf{H}}_{{Q_{2} \times 1}}^{z\theta}}^{T} ,{{\textbf{H}}_{{Q_{2} \times 1}}^{\theta z}}^{T} } \right]^{T} $$
(11)
$$ {\textbf{H}}_{{Q_{1} \times 1}}^{z} = \left[ {h_{1}^{z} [0],h_{1}^{z} [1], \ldots ,h_{1}^{z} [M]} \right]^{T} $$
(12)
$$ {\textbf{H}}_{{Q_{2} \times 1}}^{zz} = [h_{2}^{zz} [0,0],h_{2}^{zz} [0,1], \ldots ,h_{2}^{zz} [0,M], \ldots ,h_{2}^{zz} [M,0],h_{2}^{zz} [M,1],h_{2}^{zz} [M,M]]^{T} $$
(13)
$$ {\textbf{H}}_{{Q_{2} \times 1}}^{z\theta } = [h_{2}^{z\theta } [0,0],h_{2}^{z\theta } [0,1], \ldots ,h_{2}^{z\theta } [0,M], \ldots ,h_{2}^{z\theta } [M,0],h_{2}^{z\theta } [M,1],h_{2}^{z\theta } [M,M]]^{T} $$
(14)

where hi are coefficients in the Volterra kernels in Eqs. (2) and (3). Although not shown here, the vectors \({\textbf{H}}_{{}}^{\theta \theta }\) and \({\textbf{H}}_{{}}^{\theta z}\) can be similarly defined by changing the superscripts. Note that the solution assumes that the output data have zero mean, so that the coefficient h0 in Eq. (1) vanishes. The least-squared solution of Eq. (4) can then be solved with the Moore–Penrose pseudoinverse (denoted by the symbol \(\dag\)):

$$ {\textbf{H}}_{Q \times 1} = ({\textbf{r}}_{N \times Q}^{T} {\textbf{r}}_{N \times Q} )^{ - 1} {\textbf{r}}_{N \times Q}^{T} {\textbf{F}}_{N \times 1} = ({\textbf{r}}_{N \times Q} )^{\dag } {\textbf{F}}_{N \times 1} $$
(15)

The number of coefficients (Q) for the 2nd-order double-input-single-output Volterra system is given by:

$$ Q = 2Q_{1} + 4Q_{2} ,\,\,\,\,Q_{1} = (M + 1),\,\,\,\,\,Q_{2} = (M + 1)^{2} $$
(16)

2.4 Symmetry reduction

The size of the least-squares problem increases drastically with an increasing memory length, the number of inputs and model order. A considerable reduction of the problem without a loss of accuracy can be made by exploiting the symmetry of the kernels. Although symmetry is a well-known property, it is still elaborated upon here due to its necessity to reduce the memory requirements and calculation time in the identification problem. A practical and straightforward way to implement the symmetries in the Volterra equations in matrix form is also presented.

Direct kernels can always be made symmetric with respect to the time lags. For the second-order direct kernel, the relation \(h_{2}^{zz} [k_{1} ,k_{2} ] = h_{2}^{zz} [k_{2} ,k_{1} ]\) holds. For a large M, this leads to a reduction of approximately half the unknown coefficients. Similarly, for the 2nd-order cross-kernels, the pairwise symmetry relation \(h_{2}^{z\theta } [k_{1} ,k_{2} ] = h_{2}^{\theta z} [k_{2} ,k_{1} ]\) holds. The same argument can be extended to 3rd-order kernels. Considering, for instance \(h_{3}^{zzz} [k_{1} ,k_{2} ,k_{3} ]\), all six possible permutations of k1, k2, and k3 yield the same Volterra coefficient. Furthermore, the cross-kernels have the permutation \(h_{3}^{zz\theta } [k_{1} ,k_{2} ,k_{3} ] = h_{3}^{zz\theta } [k_{2} ,k_{1} ,k_{3} ] = h_{3}^{z\theta z} [k_{1} ,k_{3} ,k_{2} ] = h_{3}^{z\theta z} [k_{2} ,k_{3} ,k_{1} ] = h_{3}^{\theta zz} [k_{3} ,k_{1} ,k_{2} ] = h_{3}^{\theta zz} [k_{3} ,k_{2} ,k_{1} ]\). With the removal of redundant coefficients, the following unique terms remain for a 3rd-order cross-model:

$$ {\textbf{H}}_{W \times 1}^{red} = [({\textbf{H}}^{z} )^{T} ,({\textbf{H}}^{\theta } )^{T} ,({\textbf{H}}^{zz} )^{T} ,({\textbf{H}}^{\theta \theta } )^{T} ,({\textbf{H}}^{z\theta } )^{T} ,({\textbf{H}}^{zzz} )^{T} ,({\textbf{H}}^{\theta \theta \theta } )^{T} ,({\textbf{H}}^{zz\theta } )^{T} ,({\textbf{H}}^{\theta \theta z} )^{T} ]^{T} $$
(17)

This reduction of coefficients is significant without reducing the model’s performance. For the two-input case, the number of coefficients is given by:

$$ Q = \mathop \sum \limits_{i = 1}^{p} 2^{i} \left( {M + 1} \right)^{i} ,\quad W \approx 2(M + 1) + \mathop \sum \limits_{i = 2}^{p} i(M + 1)^{i} $$
(18)

A pragmatic way of implementing symmetry reduction is to introduce a sparse Boolean selection matrix S that populates the full vector of coefficients \({\textbf{H}}\) from the smaller vector \({\textbf{H}}^{red}\) as follows:

$$ {\textbf{H}}_{Q \times 1}^{{}} {\textbf{ = S}}_{Q \times W} {\textbf{H}}_{W \times 1}^{red} $$
(19)

For instance, if, for brevity, one considers a 2nd-order system with M = 1 with only the vertical motion as input, Eq. (19) becomes:

$$ \left[ {\begin{array}{*{20}c} {h^{z} [0]} \\ {h^{z} [1]} \\ {h^{zz} [0,0]} \\ {h^{zz} [1,0]} \\ {h^{zz} [0,1]} \\ {h^{zz} [1,1]} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {h^{z} [0]} \\ {h^{z} [1]} \\ {h^{zz} [0,0]} \\ {h^{zz} [1,0]} \\ {h^{zz} [1,1]} \\ \end{array} } \right] $$
(20)

where the symmetry \(h^{zz} [1,0]\) = \(h^{zz} [0,1][0,1]\) is enforced. In this example, the reduction of coefficients from 6 to 5 is minimal, but the effect is significant for higher orders and larger values of M. For a 3rd-order double-input–single-output system with M = 20, the number of coefficients is reduced from 76.000 to 29.000. Inserting Eq. (19) into Eq. (4), the input–output relation now becomes:

$$ {\textbf{F}}_{N \times 1} = {\textbf{r}}_{N \times Q} {\textbf{S}}_{Q \times W} {\textbf{H}}_{W \times 1}^{red} $$
(21)

Likewise, the least-squares problem with fewer numbers of unknown coefficients can now be written as:

$$ {\textbf{H}}_{W \times 1}^{red} = ({\textbf{S}}_{Q \times W}^{T} {\textbf{r}}_{N \times Q}^{T} {\textbf{r}}_{N \times Q} {\textbf{S}}_{Q \times W} )^{ - 1} {\textbf{S}}_{Q \times W}^{T} {\textbf{r}}_{N \times Q}^{T} {\textbf{F}}_{N \times 1} $$
(22)

The computational advantage is clear; the inverse in Eq. (22) now operates on a matrix with dimensions WxW rather than QxQ. After the coefficient vector \({\textbf{H}}^{red}\) is found, the full coefficient vector \({\textbf{H}}\) can simply be found by using Eq. (19).

2.5 Regularisation of the least-squares identification

Regularisation is a well-known technique in inverse problems for controlling overfitting and increasing the robustness of the model to predict outputs from new input data. The regularisation restricts the unknown parameters, adding a penalty term in the least-squares problem as follows:

$$ \min \left( {\left\| {{\textbf{F}} - {\textbf{rH}}} \right\|_{2}^{2} + \lambda^{2} \left\| {{\textbf{LH}}} \right\|_{2}^{2} } \right) $$
(23)

which is also known as the general form of Tikhonov regularisation [45]. The corresponding least-squares solution is given by:

$$ {\textbf{H}} = ({\textbf{r}}_{{}}^{T} {\textbf{r}}_{{}} + \lambda^{2} {\textbf{L}}^{T} {\textbf{L}})^{ - 1} {\textbf{r}}_{{}}^{T} {\textbf{F}} $$
(24)

Note that, for clarity, this chapter does not include the symmetry reduction (Eq. 19) in the presented equations. However, symmetry reduction is also valid for systems with regularisation. The choice of the penalty factor λ is elaborated upon later. Setting λ = 0 corresponds to no regularisation, and Eq. (24) reduces to the solution of the ordinary least-squares problem in Eq. (15). On the other hand, λ > 0 is helpful for avoiding overfitting and can help the model distinguish between actual data and noise when, for instance, the forces F are polluted with noise or when the model is imperfect, which is always the case for experimental data.

The Tikhonov matrix L can have different forms depending on the type of regularisation applied. For the simplest form of regularisation, i.e., 0th-order regularisation, L is the identity matrix. This implies that a penalty proportional to \(\left\| {\textbf{H}} \right\|_{2}^{2}\) is introduced, which controls the magnitude of the coefficients. Another form of regularisation penalises the 2nd-order derivative between the neighbouring elements, which has a smoothening effect. For a single-input 1st-order kernel and M = 3, this can be illustrated as follows:

$$ {\textbf{L}}_{{1{\text{st}}}} {\textbf{H}}^{z} = \left[ {\begin{array}{*{20}c} 1 & {\quad - 1} & {\quad 0} & {\quad 0} \\ { - 1} & {\quad 2} & {\quad - 1} & {\quad 0} \\ 0 & {\quad - 1} & {\quad 2} & {\quad - 1} \\ 0 & {\quad 0} & {\quad - 1} & {\quad 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {h_{1}^{z} [0]} \\ {h_{1}^{z} [1]} \\ {h_{1}^{z} [2]} \\ {h_{1}^{z} [3]} \\ \end{array} } \right] $$
(25)

For the 2nd-order kernel, the regularisation becomes more complicated since the smoothing should be applied in both the k1 and k2 directions. Figure 2 illustrates one element’s regularisation in a 2nd-order kernel, where the gradient in both directions is penalised. For the 3rd-order kernel, smoothing is conducted in all three directions in the k1–k2–k3 space, which is shown in the "Appendix".

Fig. 2
figure 2

Illustration of 2nd-order Tikhonov regularisation of a single point in the 2nd-order kernel

Full size image

The matrix \({\textbf{L}}\) is finally constructed as a block-diagonal matrix, where each submatrix operates on the different kernel coefficients. For example, for the 2nd-order model with two inputs:

$$ {\textbf{LH}} = \left[ {\begin{array}{*{20}c} {{\textbf{L}}_{{1{\text{st}}}} } & {} & {} & {} & {} & {} \\ {} & {{\textbf{L}}_{{1{\text{st}}}} } & {} & {} & {} & {} \\ {} & {} & {{\textbf{L}}_{{2{\text{nd}}}} } & {} & {} & {} \\ {} & {} & {} & {{\textbf{L}}_{{2{\text{nd}}}} } & {} & {} \\ {} & {} & {} & {} & {{\textbf{L}}_{{2{\text{nd}}}} } & {} \\ {} & {} & {} & {} & {} & {{\textbf{L}}_{{2{\text{nd}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\textbf{H}}^{z} } \\ {{\textbf{H}}^{\theta } } \\ {{\textbf{H}}^{zz} } \\ {{\textbf{H}}^{\theta \theta } } \\ {{\textbf{H}}^{z\theta } } \\ {{\textbf{H}}^{\theta z} } \\ \end{array} } \right] $$
(26)

Figure 3 shows an example of noisy and clean kernels. The two kernels are then identified from the same system. The output of the identified models becomes almost equal, and it is not necessarily given that the smooth kernel gives better predictions on independent validation data. However, for physical systems, the coarse shape of the noisy kernel is unrealistic. Models with noisy kernels may often be less robust than clean kernels. The 2nd-order Tikhonov regularisation guides the identification towards a minimisation of the relative change between neighbouring points, which will in turn minimise the noisiness of the kernel.

Fig. 3
figure 3

Example of a clean and noisy kernel identified from the same system. For a given input history, the output from these kernels could be very similar, but the clean kernel is more realistic for a physical system. Regularisation promotes smooth kernels during identification

Full size image

The optimal choice of λ is not trivial, and a trade-off must be made between the amount of penalty applied and the model fit. One well-documented method is the L-curve criterion [56], which is aimed at finding a minimum between the penalty norm \(\left\| {{\textbf{LH}}} \right\|_{2}\) and the residual norm of the data fit \(\left\| {{\textbf{rH}} - {\textbf{F}}} \right\|_{2}\). A typical L-curve plot is shown in Fig. 4, which is constructed by solving the least-squares problem for a range of different λ-values. It can be argued that the corner-point of the L-curve yields an optimal value for λ, as it represents the least amount of regularisation needed while still obtaining a reasonably good model fit. Thus, the regularisation is an interplay between reducing the model accuracy on the training data and smoothing the solution.

Fig. 4
figure 4

Illustration of the L-curve used to determine the optimal regularisation parameter λ

Full size image

2.6 Exponential decay regularisation

The Tikhonov matrix L can, in principle, take any form, and choosing a matrix that reflects prior knowledge of the connection between the coefficients could be efficient. Most physical systems have a fading memory property where the influence of the far past is negligible, indicating that the Volterra kernels should converge towards zero at the end of the memory. This effect can be enforced by introducing a regularisation that favours decay in the kernels. Similar ideas were implemented by Birpoutsoukis et al. and Lawson [38, 57], where both decay regularisation in the diagonal direction of the kernel and smoothing regularisation in the off-diagonal direction were used. In this work, we propose a simple form of decay regularisation. For a 1st-order kernel, the decay regularisation is defined as follows:

$$ {\textbf{L}}_{1st,decay}^{{}} (i,j) = \left( {\frac{{e^{{\frac{\gamma (j - 1)}{M}}} - 1}}{{e^{\gamma } - 1}}} \right)\,\delta_{ij} ,\quad i,j = 1,2, \ldots M + 1,\quad {\text{where}}\quad \delta_{ij} = \left\{ {\begin{array}{*{20}c} {1\,\,\,for\,\,i = j} \\ {0\,\,\,for\,\,i \ne j} \\ \end{array} } \right. $$
(27)

Here, 0 < γ ≤ ∞ is a parameter determining the steepness of the decay. The diagonal of the regularisation matrix is shown in Fig. 5, where some characteristics can be seen. (1) The curve starts at 0 and ends at 1. (2) The curve converges towards a linear curve when γ is close to 0, indicating a linear regularisation of the kernel. (3) The curve moves towards a unit step function for a high γ value, indicating that only the final value of the kernel will be penalised.

Fig. 5
figure 5

Diagonal of the first order regularisation matrix when using the decay regularisation method. Three different γ parameters are shown

Full size image

The decay regularisation matrix can also be extended to the 2nd-order kernel. The regularisation of the kernel’s diagonal is identical to the 1st-order kernel. The reduction of the first off-diagonal elements is shifted with one time step, etc. The pattern is illustrated in the first part of Fig. 6, where elements with the same letter represent the same decay, and the higher elements in the alphabet represent stronger decay regularisation. The full 2nd-order regularisation matrix is shown in the second part of Fig. 6. Here, one can see that the regularisation matrix is diagonal, since no regularisation between the kernel points is applied, only on the absolute value of each individual kernel parameter.

$$ {\textbf{L}}_{2nd,\;decay}^{{}} (i,j) = \left( {\frac{{e^{{\frac{\gamma (\max (m,q) - 1)}{M}}} - 1}}{{e^{\gamma } - 1}}} \right)\,\delta_{ij} ,\quad {\text{where}}\quad \delta_{ij} = \left\{ {\begin{array}{*{20}c} {1\,\,\,for\,\,i = j} \\ {0\,\,\,for\,\,i \ne j} \\ \end{array} } \right. $$
(28)
$$ m_{{(M + 1)^{2} }} = \{ 1,2,...,M + 1,1,2,...,M + 1,...,M + 1\} \, $$
(29)
$$ q_{{(M + 1)^{2} }} = \{ 1,1,...1,2,2,...2,...,M + 1,M + 1...,M + 1\} $$
(30)
Fig. 6
figure 6

Left: Illustration of the weight of the decay regularisation for the 2nd-order kernel. A higher number in the alphabet illustrates stronger regularisation. Right: The full 2nd-order decay regularisation matrix. Variables m and q are identification vectors mapping the point in the regularisation matrix back to the kernel

Full size image

Figure 7 shows the shape of the 2nd-order regularisation surface restacked into the k1–k2 plane. The restacking essentially extracts the diagonal elements, only placing the elements on the k1–k2 plane according to the m and q mapping vectors. The 2nd-order regularisation matrix has the same characteristics as the 1st-order regularisation matrix. It can also be seen from the figure that the regularisation surface regularises in both directions.

Fig. 7
figure 7

Shape of the 2nd-order decay regularisation mapped on the k1-k2 plane similar to the kernel. γ = 5

Full size image

Introducing the decay regularisation could be done in at least two ways: using the same value for λ, the decay regularisation of the 1st- and 2nd-order kernels or using two separate λ values. In this work, the latter choice is made. The 1st- and 2nd-order regularisation matrices are block-diagonal-independent of one another. Further inserting the decay regularisation into Eq. (15) gives:

$$ {\textbf{L}}_{1st,decay,tot} {\textbf{H}} = \left[ {\begin{array}{*{20}c} {{\textbf{L}}_{1st,decay} } & {} & {} & {} & {} & {} \\ {} & {{\textbf{L}}_{1st,decay} } & {} & {} & {} & {} \\ {} & {} & {0_{{\left( {M + 1} \right)^{2} ,\left( {M + 1} \right)^{2} }} } & {} & {} & {} \\ {} & {} & {} & {0_{{\left( {M + 1} \right)^{2} ,\left( {M + 1} \right)^{2} }} } & {} & {} \\ {} & {} & {} & {} & {0_{{\left( {M + 1} \right)^{2} ,\left( {M + 1} \right)^{2} }} } & {} \\ {} & {} & {} & {} & {} & {0_{{\left( {M + 1} \right)^{2} ,\left( {M + 1} \right)^{2} }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\textbf{H}}^{z} } \\ {{\textbf{H}}^{\theta } } \\ {{\textbf{H}}^{zz} } \\ {{\textbf{H}}^{\theta \theta } } \\ {{\textbf{H}}^{z\theta } } \\ {{\textbf{H}}^{\theta z} } \\ \end{array} } \right] $$
(31)
$$ {\textbf{L}}_{{2^{nd} ,decay,tot}} {\textbf{H}} = \left[ {\begin{array}{*{20}c} {0_{(M + 1),(M + 1)} } & {} & {} & {} & {} & {} \\ {} & {0_{(M + 1),(M + 1)} } & {} & {} & {} & {} \\ {} & {} & {{\textbf{L}}_{{2^{nd} ,decay}} } & {} & {} & {} \\ {} & {} & {} & {{\textbf{L}}_{{2^{nd} ,decay}} } & {} & {} \\ {} & {} & {} & {} & {{\textbf{L}}_{{2^{nd} ,decay}} } & {} \\ {} & {} & {} & {} & {} & {{\textbf{L}}_{{2^{nd} ,decay}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\textbf{H}}^{z} } \\ {{\textbf{H}}^{\theta } } \\ {{\textbf{H}}^{zz} } \\ {{\textbf{H}}^{\theta \theta } } \\ {{\textbf{H}}^{z\theta } } \\ {{\textbf{H}}^{\theta z} } \\ \end{array} } \right] $$
(32)
$$ {\textbf{H}}_{Q \times 1} = ({\textbf{r}}_{{}}^{T} {\textbf{r}}_{{}} + \lambda_{{1^{st} ,decay}}^{2} {\textbf{L}}_{{1^{st} ,decay,tot}}^{T} {\textbf{L}}_{{1^{st} ,decay,tot}} + \lambda_{{2^{nd} ,decay}}^{2} {\textbf{L}}_{{2^{nd} ,decay,tot}}^{T} {\textbf{L}}_{{2^{nd} ,decay,tot}}^{{}} )^{ - 1} {\textbf{r}}_{{}}^{T} {\textbf{F}} $$
(33)

where \(\lambda_{1st,decay}\) and \(\lambda_{2nd,decay}\) are the 1st- and 2nd-order decay parameters. Using this approach generates 3 unknown parameters. A pragmatic way of finding the parameters chosen here is (1) choosing parameter γ between 3 and 10; and (2) loop over different \(\lambda_{1st,decay}\) and \(\lambda_{{2^{nd} ,decay}}\) values, making a 3-dimensional L-curve with \(\left\| {{\textbf{L}}_{1st,decay,tot} {\textbf{H}}} \right\|_{2}\),\(\left\| {{\textbf{L}}_{2nd,decay,tot} {\textbf{H}}} \right\|_{2}\) and \(\left\| {{\textbf{rH}} - {\textbf{F}}} \right\|_{2}\) on the axis. Figure 8 shows an example of this. The optimal point is as near the origin as possible, reducing all three norms.

Fig. 8
figure 8

Double L-curve; the optimal point is marked in red. The Double-L Curve is from the theoretical system given in Sect. 2. (Color figure online)

Full size image

2.7 Least-squares algorithms

Note that least-squares solvers in popular programming languages (e.g., MATLAB or Python) often include a solution that utilises a truncated singular value decomposition (SVD), which is also a form of regularisation. Thus, the nonregularised solutions denoted “LSQ” (calculated by the function mldivide() in MATLAB) may include a small amount of regularisation imposed by the machine to stabilise the solution so that singular values that are small compared to machine precision are filtered out. As will be shown, however, this form of inbuilt regularisation is typically not sufficient to avoid noise magnification. Truncated SVDs are an alternative form of regularisation that is not discussed here [58].

3 Numerical validation

A numerical example is presented to evaluate the performance of the regularisation. The same example has also been used in Skyvulstad et al. [19] to identify the parametric Volterra models. The 1st-order kernel is assumed to be shaped as a rational function without instantaneous terms [59]:

$$ h_{1} = - \frac{dV}{B}e^{{\left( { - \frac{dV}{B}t} \right)}} $$
(34)

The linear model is then expanded to a nonlinear model, introducing a static nonlinearity to form a Weiner model:

$$ F = a_{1} F_{1} + a_{2} F_{1}^{2} + F_{noise} $$
(35)
$$ F_{1} = \sum\limits_{k = 0}^{M} {h_{1} [k]r[n - k]} $$
(36)

where a1 and a2 are constants, F1 is the force from the linear 1st-order kernel, and r is the input driving the system. Additive noise, \(F_{noise}\), is added to the output. The input–output data are used to train models with and without regularisation. Two input–output datasets were used:

  1. 1.

    SNR (signal-to-noise ratio) = ∞, i.e., a pure signal without added output noise (\(F_{noise} = 0\)).

  2. 2.

    SNR = 10. A signal-to-noise ratio of 10 represents imperfect experimental measurements.

The input driving the system, r, is a time series with pink noise that illustrates a scenario with energy concentrated at low frequencies, as seen for the turbulent wind spectrum. The additive noise, \(F_{noise}\), is an independent pink noise realisation. Different types of models were tested:

  1. 1.

    R0 = 0th-order Tikhonov regularisation.

  2. 2.

    R1 = 2nd-order Tikhonov regularisation separated into Low, High and Best denoting a low, high and best possible value, respectively, for the regularisation coefficient, λ2, according to the L-curve criterion. Figure 9 shows the L-curve with the chosen λ values.

  3. 3.

    LSQ = model without regularisation.

  4. 4.

    DECAY = model with a decay type of regularisation, with γ = 5.

Fig. 9
figure 9

L-Curve plot of the Volterra model with 2nd-order regularisation. Low, Best and High denote different models used

Full size image

All optimal regularisation coefficients are found by utilizing the L-curve or double L-curve. Supplementary parameters can be found in Table 1.

Table 1 Parameters of the numerical example
Full size table

All models identified on the dataset without noise gave near perfect model fits, and the suggested λ was close to zero, indicating that no regularisation was needed. This means that the Volterra model is able to model the theoretical problem, and that the regularised models are also applicable for noise-free data, even if there is no advantage of using regularisation on noise-free data with a perfect model fit. The presentation of the perfect noise-free dataset is therefore minimised.

An advantage of the Volterra series models is that the kernels can give insight into the physics of the system. Since the Volterra series model is said to model a wide range of nonlinearities, if a sufficiently high model order is used, a true set of kernels could, in theory, be found for a wide range of nonlinear systems. Furthermore, since the Volterra kernels are a generalisation of the impulse response function, the identified kernels can give insight into several aspects of the system, including (1) memory lengths for the different orders, (2) contributions from the different kernel orders, (3) time-lag effects, and (4) coupling effects between impulses with different time-lags. The kernels can also be transformed into the frequency domain in order to study the multidimensional frequency response functions to gain further insight. Both smooth and decaying kernels are expected for the physical system of self-excited forces on bridge decks, and it is therefore important to evaluate not only the performance of the models, but also the shape of the kernels.

Figure 10 shows the 1st-order kernels for the various Volterra models. The case without noise is excluded. The kernel from the LSQ model with noise has some scatter at the end of the kernel, but it is not significant. The highly regularised model (R1 high) over-smooths the kernels, while (R1, low) portrays a kernel similar to that obtained by standard least-squares. The (R1 best) model is reasonably smooth but does not fully capture the negative start values of the kernel. The same effect is seen for the R0 regularisation. The Decay model seems to predict the kernel fairly well but overshoots the negative values slightly.

Fig. 10
figure 10

1st-order kernels of the identified Volterra models. R0 and R1 denote 0th-and 2nd-order Tikhonov regularised models. Decay denotes the model with decay regularisation, and LSQ denotes the model without regularisation

Full size image

Figure 11 shows the 2nd-order kernels for the estimated Volterra models. Figure 12 shows the diagonal of the 2nd-order kernels to better compare the amplitudes of the different kernels. One can see that the LSQ model gives the noisiest kernels. The same effects can be seen on the R1, Low model, but the noise is reduced, while R1, High over smooth the 2nd-order kernel, and R1, best gives a good kernel estimation, but the top of the kernel is underestimated. Decay regularisation gives a good prediction of the kernel, and the kernel goes to zero towards the end of the memory.

Fig. 11
figure 11

2nd-order kernels for the different Volterra models identified from the theoretical input–output data. R1 denotes the model with 2nd-order Tikhonov regularisation. Decay denotes the model with decay type regularisation. LSQ denotes the model without regularisation. SNR denotes the signal-to-noise ratio

Full size image
Fig. 12
figure 12

Diagonal of the 2nd-order kernels from the models identified from the theoretical input–output data. R1 denotes the 2nd-order Tikhonov regularised model. Decay denotes the model with decay regularisation. LSQ denotes the model without regularisation

Full size image

Figure 9 shows the L-curve for the R1 models denoting high, low, and best choice for the λ factor. Figure 13 shows the double L-curve for the Decay model. Both L-curves have distinct corner regions, making it viable to extract a suitable value for λ.

Fig. 13
figure 13

Double L-curve for the SNR = 10 decay regularised model

Full size image

For most physical systems, smooth kernels are a sign that the identified model is reasonable. Nevertheless, the model needs to be validated on new datasets. For the presented numerical example, three sets of validation datasets were used: (1) pink noise validation input data with N = 10.000, with N = 10.000 pink noise training data, (2) white noise validation input data with N = 10.000, with N = 10.000 pink noise training data, and (3) white noise validation input data with N = 10.000, with N = 100.000 pink noise training data. The first case (pink noise input) has identical statistical properties as the input in the training dataset. The white noise inputs have a wider frequency content compared with the training dataset. In practical engineering, the experimental data could, quite possibly, only cover a limited range of the operating data. The model needs to be reliable and robust for these cases. Figure 14 shows some of the model predictions compared to the independent white noise validation data. It is seen from the figure that Decay and R1, best perform significantly better than the LSQ model. The increased performance for the regularised models can be explained by the increased model robustness using the regularised models.

Fig. 14
figure 14

Time-domain realisations of different Volterra models. The training data input is N = 10.000 pink noise with additive pink noise on the output, and the validation input data is N = 10.000 white noise

Full size image

The normalised mean square error (NMSE) is used to evaluate the model prediction. The NMSE is defined as:

$$ {\text{NMSE}} = 1 - \frac{{\left\| {{\textbf{x}}_{ref} - {\textbf{x}}_{pred} } \right\|_{{}}^{2} }}{{\left\| {{\textbf{x}}_{ref} - {\text{mean}}({\textbf{x}}_{ref} )} \right\|_{{}}^{2} }} $$
(37)

where \({\textbf{x}}_{ref}\) is the measured data, \({{\varvec{x}}}_{{\varvec{p}}{\varvec{r}}{\varvec{e}}{\varvec{d}}}\) is the predicted data, and \(\left\| {\textbf{x}} \right\|\) represents the second norm. The NMSE varies between 1 for a perfect fit and -∞ for a very poor fit. Table 2 shows the different model performances according to the NMSE. The model with pink noise validation data performs very well for all the models. The lengths of the training data differ for the white noise validation data, and it can be seen that the length of the training data increases all model performance with noise. All models without noise give a perfect fit for both lengths of training data, which is expected since a Volterra-type model was used to generate the data used in the numerical example. It is interesting to note that the regularised models perform better for the white noise validation data than the nonregularised ones. Even the R1, Low model has a significant performance boost compared with the pure LSQ model. It is also interesting to note that the Decay regularisation model performs the best models with noise. These observations indicate that this form of regularisation could be a good choice for decaying nonlinear systems.

Table 2 NMSE performance of the different models with different validation data and training data
Full size table

4 Wind tunnel experiments

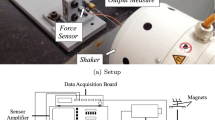
A wind tunnel experimental campaign was conducted at the Norwegian University of Science and Technology (NTNU). A forced vibration rig with the ability to excite a section model in an arbitrary prescribed vertical, horizontal, and pitching motion was used. For a description of the test rig, see the cited paper Siedziako et al.[53]. Figure 1 shows the shape of the tested section model. The beams between the bridge decks were not included in the model, and the detailing consists of two railings and a windscreen per deck. Figure 15 shows a picture of the section model mounted in the test rig. The section model is connected to a load cell at each end, measuring forces at 200 Hz. All tests were conducted in a smooth flow.

Fig. 15
figure 15

Section model mounted in the forced vibration rig in the wind tunnel at NTNU, Trondheim, Norway

Full size image

The method from Han et al. [60] was used for the extraction of self-excited forces. The method involves testing identical motions in wind and in still air to obtain the self-excited forces as the difference between the two. The test overview is summarised in Table 3. The shape of the static coefficients, shown in Fig. 16, indicates that nonlinearities in the lift and pitching moment could be present for a mean angle of attack of − 2 degrees. A mean angle of attack of -2 degrees is within reasonable operating limits for long-span bridges [61, 62]. The remainder of the tests, consisting of single harmonic and stochastic motions, were conducted at a mean angle of attack of − 2 degrees to further investigate the effect of nonlinearities. The stochastic motions are time-domain realisations of band-limited white noise with a constant spectrum between 0 and 2.5 Hz. The stochastic motions are then used as training and validation data for the Volterra models, and the single harmonic tests are utilised as a part of the validation of the models. Single degree of freedom pitching motions and two degrees of freedom combined pitching and vertical stochastic motions tests were used.

Table 3 Overview of the wind tunnel tests. T denotes the pitching motion, and TV denotes combined pitching and vertical motion
Full size table
Fig. 16
figure 16

Static coefficients. CD, CL, and CM denote drag, lift and pitching moment static coefficients. Drag is normalised to the bridge deck height, the lift is normalised to the total bridge deck width and pitching moment is normalised to the square of the bridge deck width

Full size image

5 Experimental validation

This chapter presents the modelling of the self-excited forces v Volterra models for the twin deck shown in Fig. 15. First, different Volterra models were trained on one degree of freedom (1DOF) stochastic pitching motion data. Furthermore, the models were validated using independent stochastic input motions, and the performance of the models is tested for single harmonic input motions. Last, the two degrees of freedom data are used to check the regularisation method validity of the Volterra models, including the cross-terms of vertical and pitching movement.

5.1 Single degree of freedom data

In the following, 1st-, 2nd-, and 3rd-order Volterra models with different regularisation types have been calibrated and validated for a single degree of freedom stochastic pitching motion. The stochastic motion is a time-domain realisation of coloured noise with a constant spectrum between 0 and 2.5 Hz. The training and validation data are 300 s long with a sampling rate of 66.6 Hz, giving N ~ 20.000 samples. The flow in the wind tunnel is smooth with a velocity of 12 m/s. A memory length of M = 60 is used, since more extended memory did not improve the performance. The numerical example showed that the 0th-order Tikhonov regularisation had a lower performance than the 2nd-order Tikhonov regularisation. The 0th-order regularisation is, therefore, not explored in the following. Note that the decay type of regularisation is only developed for models up to the 2nd order. The optimal λ factors were found using the L- or double L-curve. Table 4 shows the performance of the tested Volterra models. The different models are summarised as follows: (1) R1 is the 2nd-order Tikhonov regularisation model, and (2) LSQ is the least-squares identification without regularisation, using mldivide() in MATLAB. Decay denotes decay regularisation with γ = 5. The table shows that increasing the model order from 1 to 2 increases the performance in the NMSE metric, while increasing the model order to the 3rd-order gives a minor improvement. Lift and drag forces show signs of nonlinearities because of the significant performance increase from the 1st- to the 2nd-order models. The different models with the same model order perform similarly, but the nonregularised models tend to give a slightly better NMSE. The nonregularised solution is very free to adapt its coefficients but also leads to highly non-smooth kernels, as illustrated in Fig. 17b and g. Although nonregularised kernels might sufficiently reproduce the output due to their cancellation effects (i.e., large dips and large peaks in the impulse response will cancel out in the output), it can be argued that they do not reflect the physics of the problem. The regularised solution, however, gives some insight into the fluid memory effects. For instance, in Fig. 17h, it is clear that the kernel is concentrated around short time lags (k1 < 10, k2 < 10), which is not at all possible to deduce from the nonregularised solution in Fig. 17g. Interestingly, the 2nd-order model for the drag force without regularisation performs worse than the regularised versions. This can be due to the high noise-to-signal ratio of the drag force.

Table 4 NMSE values for different models. The models are trained with stochastic motion data and validated with an independent set of stochastic motion data
Full size table
Fig. 17
figure 17

Figures from self-excited lift force modelling on 12 m/s random pitching motion tests: (a–c) 1st-order kernels for different models. R1, LSQ and Decay denote 2nd-order regularisation, without regularisation and using decay regularisation, respectively. (d and f) are the L-curves for the 2nd-order regularisation models. (e, g, h) are the 2nd-order kernels for the different models

Full size image

Note that the linear benchmark of the 1st-order model is expected to perform equally well or slightly better than the well-established rational-function approximation model [59], since both are impulse-response function models.

Figures 17, 18 and 19 show the 1st- and 2nd-order kernels and the L-curves for the identified Volterra models. Figure 17 shows the lift force models. First, one can observe that both L-curves have well-defined corner points. The shape of the kernels from the Tikhonov regularisation looks far smoother than the nonregularised one. The 1st- and 2nd-order kernel should probably converge to 0 at the end of the kernel. Introducing a longer memory M was explored, but produced the same results. On the other hand, the decay kernels look more realistic than the others.

Fig. 18
figure 18

Models of the self-excited pitching moment on 12 m/s random pitching motion tests: (a–c) 1st-order kernels for different models. R1, LSQ and Decay denote 2nd-order regularisation, without regularisation and using decay regularisation, respectively. (d and f) are the L-curves for the 2nd-order regularisation models. (e, g, h) are the 2nd-order kernels for the different models

Full size image
Fig. 19
figure 19

Figures from the self-excited drag force modelling on 12 m/s random pitching motion tests: (a–c) 1st-order kernels for different models. R1, LSQ and Decay denote 2nd-order regularisation, without regularisation and using decay regularisation, respectively. (d and f) are the L-curves for the 2nd-order regularisation models. (e, g, and h) are the 2nd-order kernels for the different models

Full size image

Figure 18 shows an in-depth view of the pitching moment Volterra models. The L-curve of the model has no distinct corner point due to the lower signal–noise ratio of the measured pitching moment compared to the measured lift force. The 2nd-order Tikhonov model gives an unfavourable shape of the 1st-order kernel since it is increasing. This could be a sign of overfitting. The problem could also be due to the low nonlinearity of the data giving an almost obsolete 2nd-order part of the model, which again provides a significant number of free unknowns. The nonregularised models give very noisy kernels, as can be seen for the lift force. The decay regularisation gives very smooth kernels with high maximum values of the 2nd-order kernel for low memory lengths. This might be a sign of overfitting as well.

Figure 19 shows an in-depth view of the drag force models. The L-curve shows distinct corner points, indicating significant experimental noise. The kernels from the nonregularised models are very noisy. The 1st-order kernels from the Tikhonov models do not converge to 0. The decay kernels are very clean and are probably close to the true kernel.

5.1.1 Time-domain comparison of self-excited force

Figures 20 and 21 show comparisons of the experimental self-excited forces and predictions by the Volterra models. All 2nd-order models perform very well and provide predictions that are almost equal. The 1st-order model struggles to predict the drag and lift force and, to some extent, the pitching moment. This indicates that significant nonlinearities are present for these force components.

Fig. 20
figure 20

Measured vs. predicted forces from different models. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models. The models are trained on self-excited pitching motion experimental data and validated on an independent set of experimental data

Full size image
Fig. 21
figure 21

Measured vs. predicted forces from different models. R1 denotes 2nd-order Tikhonov regularisation models, and 1st and 2nd relate to 1st- and 2nd-order Volterra models. The models are trained on self-excited pitching motion experimental data and validated on an independent set of experimental data

Full size image

Figure 22 shows two model predictions for models trained on the same dataset. One can clearly see that not having any form of regularisation gives significantly unstable behaviour for the first M elements. This issue is not major but might cause instability issues for an unwary user trying to run time-domain simulations of a model loaded with a nonregularised Volterra model.

Fig. 22
figure 22

Comparison of the first predicted element from a regularised and a nonregularised model. Both plots are the same but with different Y-axis limits. R1 and LSQ denote the 2nd-order Tikhonov model and the nonregularised model

Full size image

5.1.2 Harmonic motion validation

For all nonlinear models, it is highly recommended to have a training dataset that covers the entire operating region of the model. However, in many cases this might not be possible for practical reasons, and it is therefore recommended to train a model that is as robust as possible. In this section, the robustness of the models is validated using harmonic input motions. The input motions are within the region of the training data but are still very different from the broadband stochastic motion used as training data.

Figures 23, 24 and 25 show a comparison between the measured and predicted forces for three different harmonic motions. The first two cycles are removed from the experimental data to remove possible transient effects. The remaining 18 cycles are then shown in the figures as light grey lines, and the mean values are shown as dark blue lines. Some general comments can be made. The 2nd-order models capture the first two peaks in the Fourier amplitudes at one and two times the harmonic motion frequency, and the 1st-order models capture the first peak. The 1st-order gives elliptical hysteresis since the model is linear.

Fig. 23
figure 23

Measured experimental and predicted drag forces for single harmonic motion. The model predictions are trained on stochastic motion experimental self-excited drag force data. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models. (Color figure online)

Full size image
Fig. 24
figure 24

Measured experimental and predicted lift forces for single harmonic motion. The model predictions are trained on stochastic motion experimental self-excited lift force data. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models. (Color figure online)

Full size image
Fig. 25
figure 25

Measured experimental and predicted pitching moments for single harmonic motion. The model predictions are trained on stochastic motion experimental self-excited pitching moment data. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models. (Color figure online)

Full size image

Figure 23 shows the predicted drag force. An accurate prediction of the drag force is challenging since the data used to identify the kernels have a high noise-to-signal ratio. The 2nd-order model predictions for the 0.8 and 1.7 Hz series is slightly off near the largest angles of attack, but all models predict nearly the same loop. For the 2.5 Hz case, the model without regularisation differs significantly from the measured loop and predictions by the other two models. This observation indicates overfitting for the nonregularised model. It is also important to note that 2.5 Hz single harmonic input motion with a 2-degree amplitude is close to the border of the applied training data since coloured noise data with a frequency content between 0 and 2.5 Hz was used. The decay model is the model that best fits the single harmonic drag data.

Figure 24 shows a comparison of the measured and predicted lift forces for single harmonic motion. The lift force damping is minimal, so the hysteresis is almost flat. For the 2.5 Hz data, the nonregularised model seems to struggle with the prediction due to overfitting. The rest of the hysteresis fits reasonably well.

Figure 25 presents a comparison of the measured and predicted lift forces for single harmonic motion. The hysteresis is almost elliptical, and the 2nd-order effects are negligible. Only minor discrepancies between the predicted and measured hysteresis data are present, which supports the observations seen earlier in this paper.

5.2 Two degrees of freedom motion

Two degrees of motion freedom, consisting of simultaneous random vertical and pitching motion, has also been tested in the wind tunnel. These two motion histories are used as inputs to the self-excited force model. 1st- to 3rd-order multi-input–single-output Volterra models have been calibrated and validated on two independent self-excited force datasets. The different model identification methods used are as follows: (1) R1 is the 2nd-order Tikhonov regularisation model, (2) LSQ is the least-squares model without regularisation using the mldivide() function in MATLAB, and (3) Decay is the decay type regularisation with γ = 5. In addition, a no-cross model is introduced, which is a higher-order Volterra model without cross-kernels. The model is introduced to investigate the effects of neglecting the cross-input nonlinearity.

The stochastic motion excited in the wind tunnel is coloured noise with a constant spectrum between 0 and 2.5 Hz. The training data and validation data are 300 s with a sampling rate of 66.6 Hz, giving N ~ 20.000 samples. For the 1st- and 2nd-order model, a memory length of M = 45 elements is used. The decreased memory lengths compared with the 1DOF tests do not reduce the performance, and it speeds up the computation and reduces the number of unknowns. Due to the high computational demand of the 3rd-order MISO models, a memory length of M = 15 is used. All λ factors were found using the L- or double L-curve. Note that the λ-factor is set equal for all kernels for the Tikhonov regularisation models. For the decay type of the model, two λ factors were introduced, one for the 1st-order kernels and one for the 2nd-order kernels, meaning that all direct and cross-terms of the same order have equal weighted regularisation. Note that for modelling of MISO models compared to SISO models, the amount of unknown greatly increases meaning that the demand for additional training data increases to avoid overfitting.

Table 5 shows the NMSE values for the different models. Nonlinearity is present for both the lift and the drag forces due to the low performance of the 1st-order Volterra models. The 3rd-order models without cross-terms and regularisation show a low performance compared to the other models, which is probably due to overfitting. The no-cross model with regularisation does not struggle nearly as much. Since the 3rd-order models perform worse than the 2nd-order models, this could be due to overfitting, but could also be related to the shorter memory lengths. The rest of the models perform relatively equally and at a high level.

Table 5 NMSE values for the models and forces
Full size table

Figure 26 shows Volterra kernels for various models trained on the experimental self-excited drag force data. The same conclusions as for the 1 DOF cases can be drawn regarding the shape of the kernels: (1) Models without regularisation have kernels that are very noisy; (2) Kernels using the 2nd-order regularisation reduces the noisiness but does not decay towards zero; and (3) Kernels from the Decay-type regularisation makes the kernels significantly cleaner. Note that all the 2nd-order models have an almost equal performance for independent validation data.

Fig. 26
figure 26

Kernels from 2nd-order Volterra models trained on experimental self-excited drag force 2DOF stochastic motion data. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models

Full size image

Figure 27 shows the time-domain realisation from various Volterra models trained on measured self-excited drag forces caused by 2DOF stochastic motion. The centre plot shows the performance of the 2nd-order models. The model performance of the 2nd-order models is good, but some underpredictions are found for the peaks, especially when the vertical motion velocity is at its highest together with high torsional displacements, which can be seen at approximately 241.8 s. Overall, the 2nd-order model performs very well.

Fig. 27
figure 27

Time-domain realisation of the drag force from various Volterra models trained on experimental self-excited 2DOF stochastic motion data. R1, LSQ and Decay denote the 2nd-order Tikhonov regularised models, the nonregularised models, and the decay regularised models, and no-cross models denote Volterra models without cross kernels

Full size image

The bottom plot in Fig. 27 shows the two 3rd-order Volterra models trained without including cross-terms for the self-excited drag force. According to Table 5, the no-cross model with regularisation performed fairly well, with some overfitting, but the no-cross model without regularisation had significant overfitting issues. This is also seen in the time-domain realisation, where one can observe that the model without regularisation has high-frequency oscillations around the experimental measurements. This is especially present in the interval of 236–237 s in the bottom part of Fig. 27. This shows that regularisation of the kernels can alleviate the problem of overfitting.

6 Conclusion

This paper explored the use of regularised least-squares identification of Volterra models for nonlinear bridge aerodynamics applications. The main findings indicate that the regularised least-squares identification of the Volterra model has several advantages. The models are more robust, the shape of the kernels becomes more realistic, and prior knowledge of the expected shape of the kernel can be used when introducing the regularisation.

The models were studied by considering a numerical example and measured self-excited forces from forced vibration wind tunnel tests. The following conclusions can be drawn from the considered examples:

  • Models identified by ordinary and regularised least-squares perform equally well if the training data are long enough and the training data and the validation data have the same frequency content. If that is not the case, then the models identified by regularised least-squares perform better than those where regularisation has not been applied.

  • For the experimental single degree of freedom motions studied, it is observed that the regularised and the nonregularised versions perform well for all considered cases. However, the regularised version’s performance is better for some single harmonic cases due to less overfitting. This is because single harmonic motions were not used to obtain the Volterra kernels.

  • The kernels obtained by nonregularised least-squares are unphysical. Tikhonov regularisation improves this, to a certain extent, while decay regularisation ensures that the kernel also decays as they should.

  • For combined vertical pitching motion, the higher-order models can predict the forces with a relatively good accuracy. Nevertheless, for the drag force, the nonregularised version of the incomplete models without cross-terms struggle to predict the forces as well as the models obtained with regularised least-squares.

Regularised Volterra model identification is a viable method for modelling nonlinear self-excited forces. It is also expected that similar models could be developed for a wider class of nonlinear bridge aerodynamics problems, including large angles of attack caused by turbulence and limit cycle oscillations.

6.1 Toolbox

The authors have supplied a MATLAB toolbox together with the manuscript.