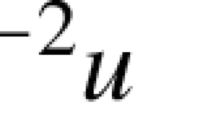Skip to main content
SpringerLink
Log in

Rogue waves on the periodic background in the high-order discrete mKdV equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

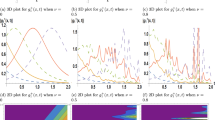
We construct new exact solutions for the high-order discrete mKdV (dmKdV) equation. The exact solutions are obtained by using the nonlinearization of spectral problem, one-, and two-fold Darboux transformations. Two families of traveling periodic waves of the high-order dmKdV equation are expressed by the Jacobi dnoidal and cnoidal elliptic functions. Since the dnoidal traveling wave is modulationally stable and the traveling cnoidal wave is modulationally unstable, the rogue waves only generated on the cnoidal wave background while the algebraic solitons propagating on the dnoidal wave background.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data availability

Data will be made availability on reasonable request.

References

  1. Ablowitz, M.J., Ladik, J.F.: Nonlinear differential-difference equations and Fourier analysis. J. Math. Phys. 17, 1011–1018 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  2. Belov, A.A., Chaltikian, K.D.: Lattice analogues of W-algebras and classical integrable equations. Phys. Lett. B 309, 268–274 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bogoyavlensky, O.I.: Integrable discretizations of the KdV equation. Phys. Lett. A 134, 34–38 (1988)

    Article  MathSciNet  Google Scholar 

  4. Bronski, J.C., Hur, V.M., Johnson, M.A.: Modulational instability in equations of KdV type, Lecture Notes in Phys, vol. 908, chap. New approaches to nonlinear waves, pp. 83–133. Springer, Cham (2016)

  5. Chen, F., Zhang, H.Q.: Periodic travelling waves and rogue waves for the higher-order modified Korteweg-de Vries equation. Commun. Nonlinear Sci. Numer. Simulat. 97, 105767 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, J.B., Pelinovsky, D.E.: Rogue periodic waves in the focusing nonlinear Schrödinger equation. Proc. R. Soc. A 474, 20170814 (2018)

    Article  MATH  Google Scholar 

  7. Chen, J.B., Pelinovsky, D.E.: Rogue periodic waves of the modified KdV equation. Nonlinearity 31, 1955–1980 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chen, J.B., Pelinovsky, D.E.: Periodic travelling waves of the Modified KdV equation and rogue waves on the periodic background. J. Nonlinear Sci. 29, 2797–2843 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chen, J.B., Pelinovsky, D.E.: Rogue waves on the background of periodic standing waves in the derivative nonlinear Schrödinger equation. Phys. Rev. E 103, 062206 (2021)

    Article  Google Scholar 

  10. Chen, J.B., Pelinovsky, D.E.: Periodic waves in the discrete mKdV equation: Modulational instability and rogue waves. Phys. D 445, 133652 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chen, J.B., Pelinovsky, D.E., Upsal, J.: Modulational instability of periodic standing waves in the derivative NLS equation. J. Nonlinear Sci. 31, 58 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chen, J.B., Pelinovsky, D.E., White, R.E.: Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation. Phys. Rev. E 100, 052219 (2019)

    Article  MathSciNet  Google Scholar 

  13. Chen, J.B., Pelinovsky, D.E., White, R.E.: Periodic standing waves in the focusing nonlinear Schrödinger equation: Rogue waves and modulation instability. Phys. D 405, 132378 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chen, M.S., Fan, E.G.: Long-time asymptotic behavior for the discrete defocusing mKdV equation. J. Nonlinear Sci. 30, 953–990 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  15. Deconinck, B., Nivala, M.: The stability analysis of the periodic traveling wave solutions of the mKdV equation. Stud. Appl. Math. 126, 17–48 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gao, X., Zhang, H.Q.: Rogue waves for the Hirota equation on the Jacobi elliptic cn-function background. Nonlinear Dyn. 101, 1159–1168 (2020)

    Article  Google Scholar 

  17. Geng, X.G., Dai, H.H., Zhu, J.Y.: Decomposition of the discrete Ablowitz-Ladik hierarch. Stud. Appl. Math. 118, 281–312 (2007)

    Article  MathSciNet  Google Scholar 

  18. Geng, X.G., Gong, D.: Quasi-periodic solutions of the discrete mKdV hierarchy. Int. J. Geom. Methods M. 10, 1250094 (2013)

    MathSciNet  MATH  Google Scholar 

  19. Geng, X.G., Li, R.M., Xue, B.: A vector Geng-Li model: New nonlinear phenomena and breathers on periodic background waves. Phys. D 434, 133270 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kharif, C., Pelinovsky, E., Slunyaev, A.: Rogue waves in the ocean. Springer, Heidelberg (2009)

    MATH  Google Scholar 

  21. Li, Q., Zhang, J.B., Chen, D.Y.: The eigenfunctions and exact solutions of discrete mKdV hierarchy with self-consistent sources via the inverse scattering transform. Adv. Appl. Math. Mech. 7, 663–674 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, R.M., Geng, X.G.: Rogue periodic waves of the sine-Gordon equation. Appl. Math. Lett. 102, 106147 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li, R.M., Geng, X.G.: Periodic-background solutions for the Yajima-Oikawa long-wave-short-wave equation. Nonlinear Dyn. 109, 1053–1067 (2022)

    Article  Google Scholar 

  24. Ma, L.Y., Zhao, H.Q., Shen, S.F., Ma, W.X.: Abundant exact solutions to the discrete complex mKdV equation by Darboux transformation. Commun. Nonlinear Sci. Numer. Simulat. 68, 31–40 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Narita, K.: Soliton solution to extended Volterra equation. J. Phys. Soc. Jpn. 51, 1682–1685 (1982)

    Article  MathSciNet  Google Scholar 

  26. Pelinovsky, D.E., White, R.E.: Localized structures on librational and rotational travelling waves in the sine-Gordon equation. Proc. R. Soc. A 476, 20200490 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  27. Peng, W.Q., Tian, S.F., Wang, X.B., Zhang, T.T.: Characteristics of rogue waves on a periodic background for the Hirota equation. Wave Motion 93, 102454 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Peregrine, D.H.: Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Series B 25, 16–43 (1983)

    Article  MATH  Google Scholar 

  29. Shen, S.F., Zhang, J., Wang, Y.X.: New Jocobi-elliptic function solutions of the semi-discrete coupled mKdV system. Phys. Lett. A 343, 148–152 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Article  Google Scholar 

  31. Tu, G.Z.: The trace identity, a powerful tool for constructing the Hamiltonian structure of integrable systems. J. Math. Phys. 30, 330–338 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  32. Tu, G.Z.: A trace identity and its applications to the theory of discrete integrable systems. J. Phys. A: Math. Gen. 23, 3903–3922 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wei, S., Zha, Q.L.: Modulation instability and rogue waves for the sixth-order nonlinear Schrödinger equation with variable coefficients on a periodic background. Nonlinear Dyn. 109, 2979–2995 (2021)

  34. Wei, S., Zha, Q.L.: Rogue waves of the sixth-order nonlinear Schrödinger equation on a periodic background. Commun. Theor. Phys. 74, 055001 (2022)

    Article  MATH  Google Scholar 

  35. Zhang, H.Q., Chen, F.: Rogue waves for the fourth-order nonlinear Schrödinger equation on the periodic background. Chaos 31, 023129 (2021)

    Article  MATH  Google Scholar 

  36. Zhang, H.Q., Chen, F., Pei, Z.J.: Rogue waves of the fifth-order Ito equation on the general periodic travelling wave solutions background. Nonlinear Dyn. 103, 1023–1033 (2021)

    Article  Google Scholar 

  37. Zhang, H.Q., Gao, X., Pei, Z.J., Chen, F.: Rogue periodic waves in the fifth-order Ito equation. Appl. Math. Lett. 107, 106464 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhang, H.Q., Liu, R., Chen, F.: Rogue waves on the double-periodic background for a nonlinear Schrödinger equation with higher-order effects. Nonlinear Dyn. 111, 645–654 (2023)

    Article  Google Scholar 

  39. Zhang, Y.F., Mei, J.Q., Hon, Y.C.: Exact soliton solutions of the discrete modified Korteweg-de Vries (mKdV) equation. Phys. Essays 23, 276–284 (2010)

    Article  Google Scholar 

  40. Zhou, H.J., Chen, Y.: Breathers and rogue waves on the double-periodic background for the reverse-space-time derivative nonlinear Schrödinger equation. Nonlinear Dyn. 106, 3437–3451 (2021)

    Article  Google Scholar 

Download references

Funding

The author declares that no funds were received during the preparation of this manuscript.

Author information

Authors and Affiliations

  1. School of Mathematics, Southeast University, Nanjing, 210096, Jiangsu, China

    Yanpei Zhen & Jinbing Chen

Authors
  1. Yanpei Zhen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinbing Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanpei Zhen.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (nb 72 KB)

Appendix A.

Appendix A.

Using the formula for addition of Jacobi elliptic function

$$\begin{aligned}{} & {} dn(\xi \pm \alpha ,k)\\{} & {} \quad =\frac{dn(\xi ,k)dn(\alpha ,k)\mp k^2sn(\xi ,k)cn(\xi ,k)sn(\alpha ,k)cn(\alpha ,k)}{1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)}, \end{aligned}$$

substituting (27) into (24), we reach

$$\begin{aligned} \begin{aligned}&-ck^2sn(\xi ,k)cn(\xi ,k)=\omega ^2dn(\xi ,k)-2\omega \\&\quad \times \frac{dn(\xi ,k)dn(\alpha ,k)+k^2sn(\xi ,k)cn(\xi ,k)sn(\alpha ,k)cn(\alpha ,k)}{1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)}\\&\quad -2\omega dn(\xi ,k)F_1+2[1+\frac{sn^2(\alpha ,k)}{cn^2(\alpha ,k)}dn^2(\xi ,k)]\\&\quad \frac{2dn(\xi ,k)dn(\alpha ,k)}{1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)}F_1\\&\quad -2\frac{sn^2(\alpha ,k)}{cn^2(\alpha ,k)}[1+\frac{sn^2(\alpha ,k)}{cn^2(\alpha ,k)}dn^2(\xi ,k)]\\&\quad \times \frac{dn(\xi ,k)dn(\alpha ,k)+k^2sn(\xi ,k)cn(\xi ,k)sn(\alpha ,k)cn(\alpha ,k)}{1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)}\\ {}&\qquad dn(\xi ,k)\\&\quad \times \frac{2dn(\xi ,k)dn(\alpha ,k)}{1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)}. \end{aligned} \end{aligned}$$

Then, we can obtain

$$\begin{aligned}{} & {} -ck^2sn(\xi ,k)cn(\xi ,k)\bigg (cn^4(\alpha ,k)[1\\{} & {} \qquad -k^2sn^2(\xi ,k)sn^2(\alpha ,k)]^2\bigg )\\{} & {} \quad =\omega ^2dn(\xi ,k)\bigg (cn^4(\alpha ,k)[1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)]^2\bigg )\\{} & {} \qquad -2\omega (dn(\xi ,k)dn(\alpha ,k)\\{} & {} \qquad +k^2sn(\xi ,k)cn(\xi ,k)sn(\alpha ,k)cn(\alpha ,k))\\{} & {} \qquad \times \bigg (cn^4(\alpha ,k)[1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)]\bigg )\\{} & {} \qquad -2\omega dn(\xi ,k)F_1\\{} & {} \qquad \times \bigg (cn^4(\alpha ,k)[1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)]^2\bigg )\\{} & {} \qquad +2[cn^2(\alpha ,k)+sn^2(\alpha ,k)dn^2(\xi ,k)]\\{} & {} \qquad 2dn(\xi ,k)dn(\alpha ,k)F_1\\{} & {} \qquad \times \bigg (cn^2(\alpha ,k)[1-k^2sn^2(\xi ,k)sn^2(\alpha ,k)]\bigg )\\{} & {} \qquad -4sn^2(\alpha ,k)cn^2(\alpha ,k)dn^2(\alpha ,k)dn^3(\xi ,k)\\{} & {} \qquad -4k^2sn^3(\alpha ,k)cn^3(\alpha ,k)\\{} & {} \qquad \times dn(\alpha ,k)sn(\xi ,k)cn(\xi ,k)dn^2(\xi ,k)\\{} & {} \qquad -4sn^4(\alpha ,k)dn^2(\alpha ,k)dn^5(\xi ,k)\\{} & {} \qquad -4k^2sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn(\xi ,k)\\ {}{} & {} \qquad cn(\xi ,k)dn^4(\xi ,k). \end{aligned}$$

Substituting (28) into the above equation and using \(cn^2(\alpha ,k)=1-sn^2(\alpha ,k),dn^2(\alpha ,k)=1-k^2sn^2(\alpha ,k)\), we have

$$\begin{aligned}{} & {} -4k^2sn(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn(\xi ,k)cn(\xi ,k)\\{} & {} \qquad +8k^4sn^3(\alpha ,k)cn(\alpha ,k)\\{} & {} \qquad \times dn(\alpha ,k)sn^3(\xi ,k)cn(\xi ,k)\\{} & {} \qquad -4k^6sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn^5(\xi ,k)cn(\xi ,k)\\{} & {} \quad =\omega ^2cn^4(\alpha ,k)dn(\xi ,k)-2k^2\omega ^2\\{} & {} \qquad sn^2(\alpha ,k)cn^4(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad +k^4\omega ^2sn^4(\alpha ,k)cn^4(\alpha ,k)sn^4(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -2\omega cn^4(\alpha ,k)dn(\alpha ,k)dn(\xi ,k)\\{} & {} \qquad +2k^2\omega sn^2(\alpha ,k)cn^4(\alpha ,k)dn(\alpha ,k)\\{} & {} \qquad sn^2(\xi ,k)dn(\xi ,k)-2k^2\omega sn(\alpha ,k)\\{} & {} \qquad \times cn^5(\alpha ,k)sn(\xi ,k)cn(\xi ,k)+2k^4\omega \\{} & {} \qquad sn^3(\alpha ,k)cn^5(\alpha ,k)sn^3(\xi ,k)cn(\xi ,k)\\{} & {} \qquad -2\omega cn^4(\alpha ,k)F_1dn(\xi ,k)+4k^2\omega \\{} & {} \qquad sn^2(\alpha ,k)cn^4(\alpha ,k)F_1sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -2k^4\omega sn^4(\alpha ,k)cn^4(\alpha ,k)F_1sn^4(\xi ,k)dn(\xi ,k)\\{} & {} \qquad +4cn^2(\alpha ,k)dn(\alpha ,k)F_1dn(\xi ,k)\\{} & {} \qquad -8k^2sn^2(\alpha ,k)cn^2(\alpha ,k)dn(\alpha ,k)F_1sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad +4k^4sn^4(\alpha ,k)cn^2(\alpha ,k)\\{} & {} \qquad \times dn(\alpha ,k)F_1sn^4(\xi ,k)dn(\xi ,k)-4sn^2(\alpha ,k)dn(\xi ,k)\\{} & {} \qquad +4k^2sn^4(\alpha ,k)dn(\xi ,k)+4sn^4(\alpha ,k)dn(\xi ,k)\\{} & {} \qquad -4k^2sn^6(\alpha ,k)dn(\xi ,k)\\{} & {} \qquad +4k^2sn^2(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -4k^4sn^4(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -4k^2sn^4(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad +4k^4sn^6(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -4k^2sn^3(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn(\xi ,k)cn(\xi ,k)\\{} & {} \qquad +4k^4sn^3(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn^3(\xi ,k)cn(\xi ,k)\\{} & {} \qquad +4k^2sn^5(\alpha ,k)cn(\alpha ,k)\times dn(\alpha ,k)sn(\xi ,k)cn(\xi ,k)\\{} & {} \qquad -4k^4sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn^3(\xi ,k)cn(\xi ,k)\\{} & {} \qquad -4sn^4(\alpha ,k)dn(\xi ,k)+8k^2sn^4(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -4k^4sn^4(\alpha ,k)sn^4(\xi ,k)dn(\xi ,k)+4k^2sn^6(\alpha ,k)dn(\xi ,k)\\{} & {} \qquad -8k^4sn^6(\alpha ,k)sn^2(\xi ,k)dn(\xi ,k)\\{} & {} \qquad +4k^6sn^6(\alpha ,k)sn^4(\xi ,k)dn(\xi ,k)\\{} & {} \qquad -4k^2sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn(\xi ,k)cn(\xi ,k)\\{} & {} \qquad +8k^4sn^5(\alpha ,k)cn(\alpha ,k)\times dn(\alpha ,k)sn^3(\xi ,k)cn(\xi ,k)\\{} & {} \qquad -4k^6sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)sn^5(\xi ,k)cn(\xi ,k). \end{aligned}$$

Collecting the coefficients of \(dn(\xi ,k)\), \(sn^2(\xi ,k)dn(\xi ,k)\), \(sn^4(\xi ,k)dn(\xi ,k)\), \(sn(\xi ,k)cn(\xi ,k)\), \(sn^3(\xi ,k)cn(\xi ,k)\) and \(sn^5(\xi ,k)cn(\xi ,k)\) yield the system of equations

$$\begin{aligned}{} & {} \omega ^2cn^4(\alpha ,k)-2\omega cn^4(\alpha ,k)dn(\alpha ,k)\nonumber \\{} & {} \quad -4sn^2(\alpha ,k)+4k^2sn^4(\alpha ,k)\nonumber \\{} & {} \quad -2\omega cn^4(\alpha ,k)F_1+4cn^2(\alpha ,k)dn(\alpha ,k)F_1=0, \nonumber \\ \end{aligned}$$
(A1)
$$\begin{aligned}{} & {} -2k^2\omega ^2sn^2(\alpha ,k)cn^4(\alpha ,k)\nonumber \\{} & {} \quad +2k^2\omega sn^2(\alpha ,k)cn^4(\alpha ,k)dn(\alpha ,k)\nonumber \\{} & {} \quad +4k^2sn^2(\alpha ,k)-4k^4sn^4(\alpha ,k)+4k^2sn^4(\alpha ,k)\nonumber \\{} & {} \quad -4k^4sn^6(\alpha ,k)\nonumber \\{} & {} \quad +4k^2\omega sn^2(\alpha ,k)cn^4(\alpha ,k)F_1\nonumber \\{} & {} \quad -8k^2sn^2(\alpha ,k)cn^2(\alpha ,k)dn(\alpha ,k)F_1=0, \end{aligned}$$
(A2)
$$\begin{aligned}{} & {} k^4\omega ^2sn^4(\alpha ,k)cn^4(\alpha ,k)-4k^4sn^4(\alpha ,k)\nonumber \\{} & {} \quad +4k^6sn^6(\alpha ,k)\nonumber \\{} & {} \quad -2k^4\omega sn^4(\alpha ,k)cn^4(\alpha ,k)F_1\nonumber \\{} & {} \quad +4k^4sn^4(\alpha ,k)cn^2(\alpha ,k)dn(\alpha ,k)F_1=0, \end{aligned}$$
(A3)
$$\begin{aligned}{} & {} -2k^2\omega sn(\alpha ,k)cn^5(\alpha ,k)\nonumber \\{} & {} \quad -4k^2sn^3(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)\nonumber \\{} & {} \quad =-4k^2sn(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k), \end{aligned}$$
(A4)
$$\begin{aligned}{} & {} 2k^4\omega sn^3(\alpha ,k)cn^5(\alpha ,k)\nonumber \\{} & {} \quad +4k^4sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)\nonumber \\{} & {} \quad =4k^4sn^3(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k), \end{aligned}$$
(A5)
$$\begin{aligned}{} & {} -4k^6sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k)=\nonumber \\{} & {} \quad -4k^6sn^5(\alpha ,k)cn(\alpha ,k)dn(\alpha ,k). \end{aligned}$$
(A6)

From (A1)-(A6), we obtain

$$\begin{aligned} \omega =\frac{2dn(\alpha ,k)}{cn^2(\alpha ,k)},\quad \alpha \in (0,K(k)). \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhen, Y., Chen, J. Rogue waves on the periodic background in the high-order discrete mKdV equation. Nonlinear Dyn 111, 12511–12524 (2023). https://doi.org/10.1007/s11071-023-08481-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08481-z

Keywords

Search

Navigation