Skip to main content
SpringerLink
Log in

Rational and semi-rational solutions to the Davey–Stewartson III equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

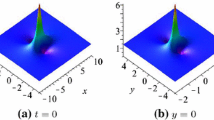
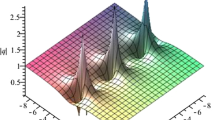
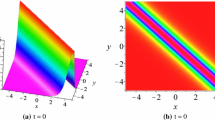
In this paper, based on the combination of Hirota’s bilinear method and long wave limit technique, we investigate rational and semi-rational solutions to the third-type Davey–Stewartson (DS III) equation and its nonlocal version. Rational solutions to the DS III equation demonstrate to be kinks, lumps and line rogue waves, while semi-rational solutions display hybrids of solitons, lumps and line rogue waves. As to the nonlocal DS III equation, we derive (semi-)rational solutions and breather solutions. Semi-rational solutions show lumps on the periodic line backgrounds, hybrids of breathers and lumps, line rogue waves and line breathers on the periodic line background.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in this published article.

References

  1. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Matter rogue waves. Phys. Rev. A. 80, 033610 (2009)

    Google Scholar 

  2. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Rogue waves as patial energy concentrators in arrays of nonlinear waveguides. Opt. Lett. 34, 3015–3017 (2009)

    Google Scholar 

  3. Horikis, T.P., Ablowitz, M.J.: Rogue waves in nonlocal media. Phys. Rev. E 95, 042211 (2017)

    MathSciNet  Google Scholar 

  4. Ganshin, A.N., Efimov, V.B., Kolmakov, G.V., Mezhov-Deglin, L.P., McClintock, P.V.E.: Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 101, 065303 (2008)

    Google Scholar 

  5. Moslem, W.M.: Erratum Langmuir rogue waves in electronpositron plasmas. Phys. Plasmas 18, 032301 (2011)

    Google Scholar 

  6. Bailung, H., Sharma, S.K., Nakamura, Y.: Observation of Peregrine solitons in a multicomponent plasma with eegative ions. Phys. Rev. Lett. 107, 255005 (2011)

    Google Scholar 

  7. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Google Scholar 

  8. Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790–795 (2010)

    Google Scholar 

  9. Dysthe, K., Krogstad, H.E., Müller, P.: Oceanic rogue waves. Annu. Rev. Fluid Mech. 40, 287–310 (2008)

    MathSciNet  MATH  Google Scholar 

  10. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373, 675–678 (2009)

    MATH  Google Scholar 

  11. Garrett, C., Gemmrich, J.: Rogue waves. Phys. Today 62, 62 (2009)

    Google Scholar 

  12. Peregrine, D.H.: Water waves, nonlinear Schrödinger equations and their solutions. Anziam J 25, 16–43 (1983)

    MATH  Google Scholar 

  13. Ankiewicz, A., Soto-Crespo, J.M., Akhmediev, N.: Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 81, 046602 (2010)

    MathSciNet  Google Scholar 

  14. Bandelow, U., Akhmediev, N.: Persistence of rogue waves in extended nonlinear Schrödinger equations: integrable Sasa-Satsuma case. Phys. Lett. A 376, 1558–1561 (2012)

    MATH  Google Scholar 

  15. Bandelow, U., Akhmediev, N.: Sasa-Satsuma equation: soliton on a background and its limiting cases. Phys. Rev. E 86, 026606 (2012)

    Google Scholar 

  16. Baronio, F., Conforti, M., Degasperis, A., Lombardo, S.: Rogue waves emerging from the resonant interaction of three waves. Phys. Rev. Lett. 111, 114101 (2013)

    Google Scholar 

  17. Guo, B.L.: Nonlinear Schrödinger equation. I: Bose-Einstein condensation and rogue waves. Adv. Math. 4, 393–399 (2011)

    MATH  Google Scholar 

  18. Ohta, Y., Yang, J.K.: General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc. R. Soc. A 468, 1716–1740 (2012)

    MathSciNet  MATH  Google Scholar 

  19. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20, 1496–1503 (1979)

    MathSciNet  MATH  Google Scholar 

  20. Gilson, C.R., Nimmo, J.J.C.: Lump solutions of the BKP solution. Phys. Lett. A. 147, 472–476 (1990)

    MathSciNet  Google Scholar 

  21. Yang, B., Yang, J.K.: Pattern transformation in higher-order lumps of the Kadomtsev-Petviashvili I equation. J. Nonlinear Sci. 32, 52 (2022)

    MathSciNet  MATH  Google Scholar 

  22. Dong, J.Y., Ling, L.M., Zhang, X.E.: Kadomtsev-Petviashvili equation: one-constraint method and lump pattern. Phys. D 432, 133152 (2022)

    MathSciNet  MATH  Google Scholar 

  23. Bender, C.M., Boettcher, S.: Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998)

    MathSciNet  MATH  Google Scholar 

  24. Bender, C.M., Brody, D.C., Jones, H.F.: Scalar quantum field theory with a complex cubic interaction. Phys. Rev. Lett. 93, 251601 (2004)

    MathSciNet  Google Scholar 

  25. Bender, C.M., Boettcher, S., Meisinger, P.N.: PT-symmetric quantum mechanics. J. Math. Phys. 40, 2201–2229 (1999)

    MathSciNet  MATH  Google Scholar 

  26. Bender, C.M., Brody, D.C., Jones, H.F., Meister, B.K.: Faster than Hermitian quantum mechanics. Phys. Rev. Lett. 98, 040403 (2007)

    MathSciNet  MATH  Google Scholar 

  27. Bender, C.M., Brody, D.C., Jones, H.F.: Extension of PT-symmetric quantum mechanics to quantum field theory with cubic interaction. Phys. Rev. D 70, 025001 (2004)

    Google Scholar 

  28. Bender, C.M.: Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 70, 947–1018 (2007)

    MathSciNet  Google Scholar 

  29. Mostafazadeh, A.: Exact PT-symmetry is equivalent to Hermiticity. J. Phys. A 36, 7081–7091 (2003)

    MathSciNet  MATH  Google Scholar 

  30. El-Ganainy, R., Makris, K.G., Christodoulides, D.N., Musslimani, Z.H.: Theory of coupled optical PT-symmetric structures. Opt. Lett. 32, 2632–2634 (2007)

    Google Scholar 

  31. Musslimani, Z.H., Makris, K.G., El-Ganainy, R., Christodoulides, D.N.: Analytical solutions to a class of nonlinear Schrödinger equations with PT-like potentials. J. Phys. A 41, 244019 (2008)

    MathSciNet  MATH  Google Scholar 

  32. Liertzer, M., Ge, L., Cerjan, A., Stone, A.D., Türeci, H.E., Rotter, S.: Pump-induced exceptional points in lasers. Phys. Rev. Lett. 108, 173901 (2012)

    Google Scholar 

  33. Annou, K., Annou, R.: Dromion in space and laboratory dusty plasma. Phys. Plasmas 19, 043705 (2012)

    Google Scholar 

  34. Konotop, V.V., Yang, J.K., Zezyulin, D.A.: Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 88, 035002 (2016)

    Google Scholar 

  35. Guo, A., Salamo, G.J., Duchesne, D., Morandotti, R., Volatier-Ravat, M., Aimez, V., Siviloglou, G.A., Christodoulides, D.N.: Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009)

    Google Scholar 

  36. Rüter, C.E., Makris, K.G., El-Ganainy, R., Christodoulides, D.N., Segev, M., Kip, D.: Observation of parity-time symmetry in optics. Nat. Phys. 6, 192–195 (2010)

    Google Scholar 

  37. Regensburger, A., Bersch, C., Miri, M.A., Onischchukov, G., Christodoulides, D.N., Peschel, U.: Parity-time synthetic photonic lattices. Nature 488, 167–171 (2012)

    Google Scholar 

  38. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Google Scholar 

  39. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear equations. Stud. Appl. Math. 139, 7–59 (2017)

    MathSciNet  MATH  Google Scholar 

  40. Hirota, R.: The direct method in soliton theory. Cambridge University Press, Cambridge, UK (2004)

    MATH  Google Scholar 

  41. Cao, Y.L., Malomed, B.A., He, J.S.: Two (2+1)-dimensional integrable nonlocal nonlinear Schrödinger equations: breather, rational and semi-rational solutions. Chaos Solitons Fractals 114, 99–107 (2018)

    MathSciNet  MATH  Google Scholar 

  42. Cao, Y.L., Rao, J.G., Mihalachec, D., He, J.S.: Semi-rational solutions for the (2+1)-dimensional nonlocal Fokas system. Appl. Math. Lett. 80, 27–34 (2018)

    MathSciNet  Google Scholar 

  43. Schul’man, E.I.: On the integrability of equations of Davey–Stewartson type. Theor. Math. Phys. 56, 131–136 (1983)

    MathSciNet  Google Scholar 

  44. Santini, P.M., Fokas, A.S.: Recursion operators and bi-Hamiltonian structures in multidimensions. I. Comm. Math. Phys. 115, 375–419 (1988)

    MathSciNet  MATH  Google Scholar 

  45. Fokas, A.S., Santini, P.M.: Recursion operators and bi-Hamiltonian structures in multidimensions. II. Comm. Math. Phys. 116, 449–474 (1988)

    MathSciNet  MATH  Google Scholar 

  46. Boiti, M., Pempinelli, F., Sabatier, P.C.: First and second order nonlinear evolution equations from an inverse spectral problem. Inverse Prob. 9, 1–37 (1993)

    MathSciNet  MATH  Google Scholar 

  47. Fokas, A.S., Ablowitz, M.J.: Linearization of the Korteweg-de Vries and Painlevé II equations. Phys. Rev. Lett. 47, 1096 (1981)

    MathSciNet  Google Scholar 

  48. Rao, J.G., Porsezian, K., He, J.S.: Semi-rational solutions of the third-type Davey–Stewartson equation. Chaos 27, 083115 (2017)

  49. Hao, X.Z., Liu, Y.P., Tang, X.Y., Li, Z.B.: The residual symmetry and exact solutions of the Davey-Stewartson III equation. Comput. Math. Appl. 73, 2404–2414 (2017)

    MathSciNet  MATH  Google Scholar 

  50. Tang, X.Y., Hao, X.Z., Liang, Z.F.: Interacting waves of Davey–Stewartson III system. Comput. Math. Appl. 74, 1311–1320 (2017)

    MathSciNet  MATH  Google Scholar 

  51. Fu, H.M., Ruan, C.Z., Hu, W.Y.: Soliton solutions to the nonlocal Davey–Stewartson III equation. Mod. Phys. Lett. B 35, 2150026 (2021)

    MathSciNet  Google Scholar 

  52. Shi, C.Y., Fu, H.M., Wu, C.F.: Soliton solutions to the reverse-time nonlocal Davey–Stewartson III equation. Wave Motion 104, 102744 (2021)

    MathSciNet  MATH  Google Scholar 

  53. Li, M., Hu, W.K., Wu, C.F.: Rational solutions of the classical Boussinesq-Burgers system. Nonlinear Dyn. 94, 1291–1302 (2018)

    Google Scholar 

  54. Zhang, X.E., Xu, T., Chen, Y.: Hybrid solutions to Mel’nikov system. Nonlinear Dyn. 94, 2841–2862 (2018)

    Google Scholar 

  55. Zhang, Y.S., Rao, J.G., Porsezian, K., He, J.S.: Rational and semi-rational solutions of the Kadomtsev–Petviashvili-based system. Nonlinear Dyn. 95, 1133–1146 (2019)

    MATH  Google Scholar 

  56. Peng, W.Q., Tian, S.F., Zhang, T.T., Fang, Y.: Rational and semi-rational solutions of a nonlocal (2+1)-dimensional nonlinear Schrödinger equation. Math. Meth. Appl. Sci. 42(18), 6865–6877 (2019)

    MATH  Google Scholar 

  57. Xia, P., Zhang, Y., Zhang, H.Y., Zhuang, Y.D.: Some novel dynamical behaviours of localized solitary waves for the Hirota-Maccari system. Nonlinear Dyn. 108, 533–541 (2022)

    Google Scholar 

  58. Rao, J.G., Zhang, Y.S., Fokas, A.S., He, J.S.: Rogue waves of the nonlocal Davey–Stewartson I equation. Nonlinearity 31, 4090–4107 (2018)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

The work is supported by National Natural Science Foundation of China (Grant Nos. 11871336, 12175155) and Shanghai Frontier Research Institute for Modern Analysis.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, CMA-Shanghai, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Sheng-Nan Wang & Guo-Fu Yu

Authors
  1. Sheng-Nan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guo-Fu Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sheng-Nan Wang.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the research effort and the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Rational solution for the DS III with \(N=4\) is expressed in the following

$$\begin{aligned} q&=\Big (108 x^4-576 x^3 y+(-1056 \textrm{i} t\\&\quad +2144 t^2+1056 y^2+648) x^2\\&\quad +768y(\textrm{i} t-\frac{53}{12} t^2-y^2-\frac{39}{16}) x+192 y^4\\&\quad +(384 \textrm{i} t+1664 t^2+864) y^2+1920 \textrm{i} t^3+3600 t^4\\&\quad +1440\textrm{i} t +5928 t^2+2457\Big ) \Big /\Big (108 x^4-576 x^3 y\\&\quad +(2144 t^2+1056 y^2+936)x^2\\&\quad +(-3392 t^2 y-768 y^3-2448 y) x+192 y^4\\&\quad +(1664 t^2+1248) y^2+3600 t^4+4744 t^2+1521\Big ). \end{aligned}$$

Semi-rational solution for the DS III with \(N=3\) admits the explicit form

$$\begin{aligned} q&=\Big ((136 \textrm{i} x^2+(-136 \textrm{i} y+96 \textrm{i}) x+34 \textrm{i}y^2\\&\quad -48 \textrm{i} y-64-19 \textrm{i}+612 \textrm{i}t^2+(-408\\&\quad +192 \textrm{i}) t) e^{x+2 y+3 t-2 \pi }+408 \textrm{i} t+612 t^2+136 x^2\\&\quad -136 x y+34 y^2-51\Big )\Big /\Big ((136 x^2+(-136 y+96)x\\&\quad +612 t^2+34 y^2+192 t-48 y+49) e^{x+2 y+3 t-2 \pi }\\&\quad +612 t^2+136 x^2-136 x y+34 y^2+17\Big ). \end{aligned}$$

Semi-rational solution for DS III with \(N=4\) is written as

$$\begin{aligned} q&=\Big ((2312 \textrm{i} x^2+(-2312 \textrm{i} y-1632 \textrm{i} )x+578\textrm{i} y^2\\&\quad +816 \textrm{i} y-1088-323\textrm{i}+10404 \textrm{i} t^2 \\&\quad +(-6936+3264 \textrm{i}) t) e^{-x-2 y+3 t-\frac{1}{2} x}\\&\quad +(2312 \textrm{i} x^2+(-2312 \textrm{i} y+1632 \textrm{i}) x\\&\quad +578\textrm{i} y^2-816 \textrm{i} y-1088-323 \textrm{i}+10404\textrm{i} t^2 \\&\quad +(-6936+3264 \textrm{i}) t) e^{x+2 y+3 t-\frac{1}{2} \pi }+(-4624 x^2\\&\quad +4624 x y-1156 y^2-314-4352\textrm{i}\\&\quad -20808 t^2+(-13056-13872 \textrm{i}) t)e^{6 t-\pi }\\&\quad +6936 \textrm{i}t+10404 t^2+2312 x^2\\&\quad -2312 x y+578 y^2-867\Big )\Big /\Big ((2312 x^2\\&\quad +(-2312 y-1632)x+10404 t^2\\&\quad +578 y^2+3264 t+816 y\\&\quad +833)e^{-x-2 y+3 t-\frac{1}{2} \pi }\\&\quad +(2312 x^2+(-2312 y+1632)x\\&\quad +10404 t^2+578 y^2+3264t\\&\quad -816 y+833) e^{x+2 y+3 t-\frac{1}{2} \pi }\\&\quad +(20808 t^2+4624 x^2-4624 x y\\&\quad +1156 y^2+13056 t+2626) e^{6t-\pi }+10404 t^2\\&\quad +2312 x^2-2312 x y+578y^2+289\Big ). \end{aligned}$$

Semi-rational solution for the nonlocal DS III with \(N=3\) has the expression

$$\begin{aligned} q&=\Big (((24\textrm{i}x^2+(-24\textrm{i}y-48)x+108\textrm{i}t^2\\&\quad +6\textrm{i}y^2-69\textrm{i}-240t+24y)\sqrt{15}\\&\quad +168x^2+(336\textrm{i}-168y)x+144\textrm{i}t-168\textrm{i}y\\&\quad +756t^2+42y^2+29)e^{\frac{1}{2}\textrm{i}x-\frac{1}{2}\textrm{i}y-\frac{1}{2}\pi }+576\textrm{i}t\\&\quad +864t^2+192x^2-192xy+48y^2\\&\quad -72\Big )\Big /\Big ((-192\sqrt{15}t+192x^2\\&\quad +(384\textrm{i}-192y)x-192\textrm{i}y+864t^2+48y^2-8)\\&\quad e^{\frac{1}{2}\textrm{i}x-\frac{1}{2}\textrm{i}y-\frac{1}{2}\pi }+864t^2+192x^2-192xy+48y^2+24\Big ). \end{aligned}$$

Semi-rational solution for the nonlocal DS III with \(N=4\) owns the form

$$\begin{aligned} q&=\Big (((-1620\textrm{i} t^2-36\textrm{i} x^2+435\textrm{i}+1800 t-480 x)\sqrt{5}\\&\quad -360\textrm{i}t+960\textrm{i}x-3240 t^2-720 x^2\\&\quad -210)e^{-\frac{2}{3} \textrm{i} x-\frac{9}{9} \sqrt{5} t+\eta }+((435 \textrm{i}-360 \textrm{i} x^2\\&\quad -1620 \textrm{i} t^2+1800 t+480 x) \sqrt{5}-360\textrm{i}t\\&\quad -960\textrm{i}x-3240 t^2-720 x^2-210)e^{\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }\\&\quad +((-2592 \textrm{i} t^2-576 \textrm{i} x^2-520 \textrm{i}+1440 t) \sqrt{5}+6192 \textrm{i} t\\&\quad +648 t^2+144 x^2-1814)e^{-\frac{10}{9} \sqrt{5} t+2 \eta }-3240\textrm{i} t \\&\quad -4860 t^2-1080 x^2+405\Big ) \Big /\Big ((1440 \textrm{i} x\\&\quad +1080 \sqrt{5} t-4860 t^2-1080 x^2+45)e^{-\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }\\&\quad +(-1440 \textrm{i} x-4860 t^2+1080 \sqrt{5} t-1080 x^2\\&\quad +45)e^{\frac{2}{3} \textrm{i} x-\frac{5}{9} \sqrt{5} t+\eta }+(-5832 t^2+2592 \sqrt{5} t-1296 x^2\\&\quad -1602)e^{-\frac{10}{9} \sqrt{5} t+2 \eta }-4860 t^2-1080 x^2-135\Big ). \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, SN., Yu, GF. Rational and semi-rational solutions to the Davey–Stewartson III equation. Nonlinear Dyn 111, 7635–7655 (2023). https://doi.org/10.1007/s11071-022-08219-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08219-3

Keywords

Search

Navigation