Joint interface modeling and characterization of lap-jointed beams

Abstract

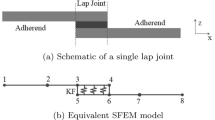
This work explores explicit reduced-order modeling of linear and nonlinear joint interface effects on the overall dynamic response of free-free and cantilever lap-jointed beam structures. Joint interfaces are a significant source of uncertainties in assembled structures due to their inherent nonlinearities. These nonlinearities create amplitude-dependent frequency and damping characteristics in the system’s response. The dynamic variability of jointed structures and their wide range of use makes it necessary to model joint interface characteristics accurately and simply. Additionally, it is desired to define joint parameters that are intuitive and easy to tune to realistic systems. To accomplish this, the linear and nonlinear joint interface effects will be explicitly modeled with various springs and dampers at a localized point along the beam. The assembled beams are modeled with the Euler–Bernoulli beam theory, while the joint effects are considered by partitioning the beam and implementing the damping and stiffness coefficients into the continuity equations. The influence of the modeled joint interface effects on the system’s response, linear properties and nonlinear trends is explored and discussed. This work develops a localized joint model which is beneficial to qualitatively understand the joint interface effects on the system’s linear and nonlinear properties. However, a distributed joint model with area-dependent forces is needed to quantitatively simulate the interface kinematics and better model the characteristics of the assembled lap-joint beam structure.

Appendix

The solution to of each mode shape function can be shown as:

$$ \phi_{L} \left( x \right) = A{\text{sin}}\left( {\beta_{1} x} \right) + B{\text{cos}}\left( {\beta_{1} x} \right) + C{\text{sinh}}\left( {\beta_{1} x} \right) + D{\text{cosh}}\left( {\beta_{1} x} \right) $$

(A1)

$$ \phi_{JL} \left( x \right) = A_{J} {\text{sin}}\left( {\beta_{2} x} \right) + B_{J} {\text{cos}}\left( {\beta_{2} x} \right) + C_{J} {\text{sinh}}\left( {\beta_{2} x} \right) + D_{J} {\text{cosh}}\left( {\beta_{2} x} \right) $$

(A2)

$$ \phi_{JR} \left( x \right) = \overline{E}_{J} {\text{sin}}\left( {\beta_{2} x} \right) + F_{J} {\text{cos}}\left( {\beta_{2} x} \right) + G_{J} {\text{sinh}}\left( {\beta_{2} x} \right) + H_{J} {\text{cosh}}\left( {\beta_{2} x} \right) $$

(A3)

$$ \phi_{R} \left( x \right) = \overline{E}{\text{sin}}\left( {\beta_{1} x} \right) + F{\text{cos}}\left( {\beta_{1} x} \right) + G{\text{sinh}}\left( {\beta_{1} x} \right) + H{\text{cosh}}\left( {\beta_{1} x} \right) $$

(A4)

where ${\beta }_{1}$ and ${\beta }_{2}$ are the trivial solutions or roots of the determinant function. The roots of the determinant function are derived from a matrix that contains the continuity equations and boundary conditions. Each mode has coefficients and a unique root. There are two roots since there are two cross-sectional areas and area MOI throughout the length of the beam. Furthermore, ${\beta }_{1}$ is the root associated with the mode shapes for the extremity partitions, while ${\beta }_{2}$ is linked to the partitions in the joint overlap region.

$$ \beta_{2} = \sqrt[4]{{\frac{{EI_{1} A_{2} }}{{EI_{2} A_{1} }}}}\beta_{1} $$

(A5)

The following orthogonality conditions are applied which state:

$$ \begin{aligned} \delta_{ij} = & \rho \left[ {A_{1} \mathop \smallint \limits_{0}^{{L_{1} }} \left( {\phi_{L,i} \left( x \right)} \right)^{2} dx + A_{2} \mathop \smallint \limits_{{L_{1} }}^{S} \left( {\phi_{JL,i} \left( x \right)} \right)^{2} dx + A_{2} \mathop \smallint \limits_{S}^{{L_{2} }} \left( {\phi_{JR,i} \left( x \right)} \right)^{2} dx + A_{1} \mathop \smallint \limits_{{L_{2} }}^{L} \left( {\phi_{R,i} \left( x \right)} \right)^{2} dx} \right] \\ & + M_{t} \left( {\phi_{R,i} \left( L \right)} \right)^{2} + J\left( {\phi^{\prime}_{R,i} \left( L \right)} \right)^{2} \\ \end{aligned} $$

(A6)

The equation for the linear natural frequency of each mode is calculated with the following orthogonality condition.

$$ \begin{aligned} \omega_{i}^{2} = & EI_{1} \mathop \smallint \limits_{0}^{L_1} \left( {\phi^{\prime\prime}_{L,i} \left( x \right)} \right)^{2} dx + EI_{2} \mathop \smallint \limits_{L_1}^{S} \left( {\phi^{\prime\prime}_{JL,i} \left( x \right)} \right)^{2} dx + EI_{2} \mathop \smallint \limits_{S}^{L_2} \left( {\phi^{\prime\prime}_{JR,i} \left( x \right)} \right)^{2} dx \\ & + EI_{1} \mathop \smallint \limits_{L_2}^{L} \left( {\phi^{\prime\prime}_{R,i} \left( x \right)} \right)^{2} dx + K_{L} \left( {\left( {\phi_{JR,i} \left( s \right) - \phi_{JL,i} \left( s \right)} \right)} \right)^{2} + K_{\theta } \left( {\left( {\phi^{\prime}_{JR,i} \left( s \right) - \phi^{\prime}_{JL,i} \left( s \right)} \right)} \right)^{2} \\ \end{aligned} $$

(A7)