When Hopf meets saddle: bifurcations in the diffusive Selkov model for glycolysis

Abstract

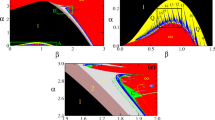
We study the linear instabilities and bifurcations in the Selkov model for glycolysis with diffusion. We show that this model has a zero wave-vector, finite frequency Hopf bifurcation, which is a forward or supercritical bifurcation, to a growing oscillatory but spatially homogeneous state and a saddle-node bifurcation, which is a backward or subcritical bifurcation, to a growing inhomogeneous state with a steady pattern characterised by a finite wavevector. We further demonstrate that by tuning the relative diffusivity of the two concentrations, it is possible to make both the instabilities to occur at the same point in the parameter space, leading to an unusual type of codimension-two bifurcation. We then show that in the vicinity of this codimension-two bifurcation, the initial conditions decide whether a spatially uniform oscillatory or a spatially periodic steady pattern emerges in the long time limit. It is also possible to form a co-existing patterned and time-periodic state by fine-tuning the diffusivity ratio for moderate values, in qualitative agreement with recent experimental studies.

Appendices

Appendix A: Explicit values of the different coefficients

The coefficients ${\tilde{C}}_1,{\tilde{C}}_2,{\tilde{D}}_1,{\tilde{D}}_2, {\tilde{F}}_2,{\tilde{G}}_1,{\tilde{G}}_2,{\tilde{H}}_1,{\tilde{H}}_2$ are given by

$$\begin{aligned} {\tilde{C}}_1= & {} -\frac{i\omega _0}{3\omega _0^2}(1+\omega _0^2),\,{\tilde{C}}_2=\frac{(1+2i\omega _0)}{6\omega _0^2}(1+\omega _0^2) , \end{aligned}$$

(A1)

$$\begin{aligned} {\tilde{D}}_1= & {} \frac{(D-1)}{9}(1+\omega _0^2),\nonumber \\ {\tilde{D}}_2= & {} -\frac{(D+7)(D-1)}{72D}(1+\omega _0^2),\end{aligned}$$

(A2)

$$\begin{aligned} F_1= & {} 0,\,{\tilde{F}}_2=-\frac{(1+\omega _0^2)}{\omega _0^2},\end{aligned}$$

(A3)

$$\begin{aligned} {\tilde{G}}_1= & {} \frac{i\omega _0+2D/(D-1)}{-\omega _0^2+2i\omega _0(D+1)/(D-1)}(1+\omega _0^2)\nonumber \\{} & {} \left[ 1+\omega _0^2 \left( -\frac{3D+1}{2D}+\frac{i\omega _0}{\omega _0^2}\right) \right] ,\end{aligned}$$

(A4)

$$\begin{aligned} {\tilde{G}}_2= & {} -\frac{i\omega _0+1+2/(D-1)}{-\omega _0^2+2i\omega _0(D+1)/(D-1)}(1+\omega _0^2)\nonumber \\{} & {} \left[ 1+\omega _0^2 \left( -\frac{3D+1}{2D}+\frac{i\omega _0}{\omega _0^2}\right) \right] ,\end{aligned}$$

(A5)

$$\begin{aligned} {\tilde{H}}_1= & {} \frac{i\omega _0+2D/(D-1)}{-\omega _0^2+2i\omega _0(D+1)/(D-1)}(1+\omega _0^2)\nonumber \\{} & {} \left[ 1+\omega _0^2 \left( -\frac{3D+1}{2D}+\frac{i\omega _0}{\omega _0^2}\right) \right] ,\end{aligned}$$

(A6)

$$\begin{aligned} {\tilde{H}}_2= & {} -\frac{i\omega _0+1+2/(D-1)}{-\omega _0^2+2i\omega _0(D+1)/(D-1)}(1+\omega _0^2)\nonumber \\{} & {} \left[ 1+\omega _0^2 \left( -\frac{3D+1}{2D}+\frac{i\omega _0}{\omega _0^2}\right) \right] . \end{aligned}$$

(A7)

The coefficients $l_1,\,l_2,\,l_3,\,l_4$ are given by

$$\begin{aligned} l_1= & {} b_c\left( {\tilde{C}}_2 + {\tilde{C}}_2^*+2{\tilde{F}}_2+{\tilde{C}}_1\frac{i\omega _0-\omega _0^2}{\omega _0^2}\right. \nonumber \\{} & {} \left. + {\tilde{C}}_1^* \frac{-i\omega _0-\omega _0^2}{\omega _0^2} + \frac{{\tilde{C}}_1+{\tilde{C}}_1^*}{\omega _0^2}\right) -3,\end{aligned}$$

(A8)

$$\begin{aligned} l_2= & {} b_c\left[ \left( {\tilde{G}}_2+{\tilde{G}}_2^*+{\tilde{H}}_2+{\tilde{H}}_2^*-\frac{-k_c^2}{\omega _0^2}\right) \right. \nonumber \\{} & {} \left. + \frac{{\tilde{G}}_1+{\tilde{G}}_1^*+{\tilde{H}}_1+{\tilde{H}}_1^*}{\omega _0^2}\right] -\left( 4+\frac{2}{D}\right) ,\end{aligned}$$

(A9)

$$\begin{aligned} l_3= & {} 2b_c\left[ {\tilde{D}}_2+{\tilde{F}}_2-\frac{\omega _0^2-k_c^2}{\omega _0^2}{\tilde{D}}_1\right] +\frac{2b_c}{\omega _0^2} {\tilde{D}}_1\nonumber \\{} & {} -\frac{3}{2}\left( 1+\frac{1}{D}\right) ,\end{aligned}$$

(A10)

$$\begin{aligned} l_4= & {} 2b_c\left( {\tilde{G}}_2^*+{\tilde{H}}_2^*+{\tilde{F}}_2\right) -\frac{i\omega _0+\omega _0^2}{\omega _0^2} {\tilde{G}}_1^*\nonumber \\{} & {} +\frac{i\omega _0-\omega _0^2}{\omega _0^2}{\tilde{H}}_1+ \frac{{\tilde{G}}_1^*+{\tilde{H}}_1}{\omega _0^2}-\left( 5+\frac{1}{D}\right) . \end{aligned}$$

(A11)

Linear instabilities

The linear stability of FP2 can be easily ascertained by taking Eq. (40) and setting $R=0$. This gives

$$\begin{aligned} \dot{A}_2= & {} \left[ \frac{1}{2}(1-\omega _0^4)+\frac{2D}{(D-1)^4}(D^2-6D+1)\right] \epsilon _1A_2 \nonumber \\{} & {} -\left[ (1-\omega _0)^4 + \frac{4D(D+1)^2}{(D-1)^4}\right] \epsilon _2A_2\nonumber \\{} & {} +2b_cA_2^3(1+\omega _0^2)\left[ -\frac{1}{\omega _0^2} -\frac{(D+7)(D-1)}{72D}\right. \nonumber \\{} & {} \left. + 2\frac{D-1}{9\omega _0^2} \frac{D+1}{(D-1)^2} \right. \nonumber \\{} & {} \left. + \frac{2}{\omega _0^2}\frac{D-1}{9}\right] \nonumber \\- & {} \frac{3}{2D}(D+1)A_2^3. \end{aligned}$$

(B1)

Including the fifth-order term, the dynamical equation for $A_2$ is given by ($R=0$)

$$\begin{aligned} \dot{A}_2= & {} \left[ \frac{1}{2}(1-\omega _0^4)+\frac{2D}{(D-1)^4}(D^2-6D+1)\right] \epsilon _1A_2\nonumber \\{} & {} -\left[ (1-\omega _0)^4 + \frac{4D(D+1)^2}{(D-1)^4}\right] \epsilon _2A_2\nonumber \\{} & {} +l_3 A_2^3 - \Gamma A_2^5, \end{aligned}$$

(B2)

with $\Gamma >0$.