Skip to main content
SpringerLink
Log in

Prediction of dynamic systems driven by Lévy noise based on deep learning

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

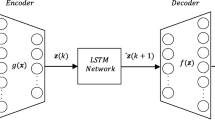
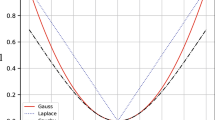
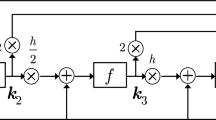
Abstract

Predicting strongly noise-driven dynamic systems has always been a difficult problem due to their chaotic properties. In this study, we investigated the prediction of dynamic systems driven by strong noise intensities, which proves that deep learning can be applied in diverse fields. This is the first study that uses deep learning algorithms to predict dynamic systems driven by strong noise intensities. We examined the effect of hyperparameters in deep learning and introduced an improved algorithm for prediction. Several numerical examples are presented to illustrate the performance of the proposed algorithm, including the Lorenz system and the Rössler system driven by noise intensities of 0.1, 0.5, 1, and 1.25. All the results suggest that the proposed improved algorithm is feasible and effective for predicting strongly noise-driven dynamic systems. Furthermore, the influences of the number of neurons, the spectral radius, and the regularization parameters are discussed in detail. These results indicate that the performances of the machine learning techniques can be improved by appropriately constructing the neural networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. For part of the code of the IRC algorithm, we have made it public at https://github.com/Lukas22eee/IRC-algorithm.

References

  1. Manjunath, G., Jaeger, H.: Echo state property linked to an input: exploring a fundamental characteristic of recurrent neural networks. Neural Comput. 25(3), 671–696 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Fan, H., Jiang, J., Zhang, C., et al.: Long-term prediction of chaotic systems with machine learning. Phys. Rev. Res. 2(1), 012080 (2020)

    Article  Google Scholar 

  3. Lukosevicius, M., Jaeger, H.: Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 3(3), 127–149 (2009)

    Article  MATH  Google Scholar 

  4. Tan, J.: Numerical solutions and applications of stochastic time-delay systems excited by Poisson white noise. Tianjin university, PhD dissertation (2010)

  5. Jaeger, H.: Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304(5667), 78–80 (2004)

    Article  Google Scholar 

  6. Hunt, B., Pathak, J., et al.: Reservoir observers: model-free inference of unmeasured variables in chaotic systems. Chaos Interdiscip. J. Nonlinear Sci. 27(4), 041102 (2017)

    Article  Google Scholar 

  7. Kengo, N., Yoshitaka, S.: Machine-learning inference of fluid variables from data using reservoir computing. Phys. Rev. E 98(2), 023111 (2018)

    Article  Google Scholar 

  8. Cestnik, R., Abel, M.: Inferring the dynamics of oscillatory systems using recurrent neural networks. Chaos 29, 063128 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Khovanov, I.A.: Stochastic approach for assessing the predictability of chaotic time series using reservoir computing. Chaos 31, 083105 (2021)

    Article  MathSciNet  Google Scholar 

  10. Maass, W., Natschlager, T., Markram, H.: Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14(11), 2531–2560 (2002)

    Article  MATH  Google Scholar 

  11. Carroll, T.L.: Using reservoir computers to distinguish chaotic signals. Phys. Rev. E 98(5), 052209 (2018)

    Article  Google Scholar 

  12. Vlachas, P.R., Pathak, J., Hunt, B.R., et al.: Backpropagation algorithms and reservoir computing in recurrent neural networks for the forecasting of complex spatiotemporal dynamics. Neural Netw. 126(115), 191–217 (2020)

    Article  Google Scholar 

  13. Falahian, R., Mehdizadeh Dastjerdi, M., Molaie, M., et al.: Artificial neural network-based modeling of brain response to flicker light. Nonlinear Dyn. 81, 1951–1967 (2015)

    Article  MathSciNet  Google Scholar 

  14. Liu Qi, Xu., Yong, L.Y., et al.: Fixed-interval smoothing of an aeroelastic airfoil model with cubic or free-play nonlinearity in incompressible flow. Acta Mech. Sin. 37(7), 1168–1182 (2021)

    Article  MathSciNet  Google Scholar 

  15. Itoh, Y., Uenohara, S., Adachi, M., et al.: Reconstructing bifurcation diagrams only from time-series data generated by electronic circuits in discrete-time dynamical systems. Chaos 30(1), 013128 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhang, C., Jiang, J., Qu, S.X., et al.: Predicting phase and sensing phase coherence in chaotic systems with machine learning. Chaos 30(7), 073142 (2020)

    MathSciNet  Google Scholar 

  17. Pathak, J., Hunt, B., Girvan, M., et al.: Model-free prediction of large spatiotemporally chaotic systems from data: a reservoir computing approach. Phys. Rev. Lett. 120(2), 024102 (2018)

    Article  Google Scholar 

  18. Cui, H., Liu, X., Li, L.: The architecture of dynamic reservoir in the echo state network. Chaos Interdiscip. J. Nonlinear Sci. 22(3), 033127 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Jaeger, H., Haas, H.: Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304(5667), 78–80 (2004)

    Article  Google Scholar 

  20. Pathak, J., Lu, Z., Hunt, B.R., et al.: Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos Interdiscip. J. Nonlinear Sci. 27(12), 121102 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Pathak, J., Wikner, A., Fussell, R., et al.: Hybrid forecasting of chaotic processes: using machine learning in conjunction with a knowledge-based model. Chaos 28(4), 041101 (2018)

    Article  MathSciNet  Google Scholar 

  22. Ma, S.: Research on very low frequency seismic wave detection based on stochastic resonance under Levy noise. Northwestern Polytechnical University, MA thesis (2018)

  23. Leccardi, M.: Comparison of three algorithms for Lévy noise generation (2008)

  24. Xu, Y., Feng, J., Li, J., Zhang, H.: Lévy noise induced switch in the gene transcriptional regulatory system. Chaos 23(1), 013110 (2013)

    Article  MathSciNet  Google Scholar 

  25. Lu, Y., Duan, J.: Discovering transition phenomena from data of stochastic dynamical systems with Lévy noise. Chaos Interdiscip. J. Nonlinear Sci. 30(9), 093110 (2020)

    Article  MATH  Google Scholar 

  26. Brešar, M., Boškoski, P., Horvat, M.: Detection of coupling in Duffing oscillator systems. Chaos Interdiscip. J. Nonlinear Sci. 31(6), 063130 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  27. Lin, Z.F., Li, J., Wu, J., et al.: Effect of the policy and consumption delay on the amplitude and length of business cycle. Chaos 30(10), 103124 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Zeng, C., Yang, Q.: Dynamics of the stochastic Lorenz chaotic system with long memory effects. Chaos Interdiscip. J. Nonlinear Sci. 25(12), 123114 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The research was supported by the National Natural Science Foundation of China (NNSFC) (Grant No. 11902234), Natural Science Basic Research Program of Shaanxi (Program No. 2020JQ-853), Shaanxi Provincial Department of Education Youth Innovation Team Scientific Research Project (Program No. 22JP025), and the Young Talents Development Support Program of Xi’an University of Finance and Economics. T.K. has been supported by the National Science Centre, Poland, OPUS Programme (Project No. 2021/43/B/ST8/00641).

Author information

Authors and Affiliations

  1. School of Statistics, Xi’an University of Finance and Economics, Xi’an, 710100, People’s Republic of China

    Zi-Fei Lin, Yan-Ming Liang & Jia-Li Zhao

  2. Xi’an University of Finance and Economics, China (Xi’an) Institute for Silk Road Research, Xi’an, 710100, People’s Republic of China

    Zi-Fei Lin & Jiao-Rui Li

  3. Division of Dynamics, Lodz University of Technology, Stefanowskiego 1/15, 90-924, Lodz, Poland

    Tomasz Kapitaniak

Authors
  1. Zi-Fei Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan-Ming Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jia-Li Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jiao-Rui Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Tomasz Kapitaniak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zi-Fei Lin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, ZF., Liang, YM., Zhao, JL. et al. Prediction of dynamic systems driven by Lévy noise based on deep learning. Nonlinear Dyn 111, 1511–1535 (2023). https://doi.org/10.1007/s11071-022-07883-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07883-9

Keywords

Search

Navigation