1 Introduction

Regulations imposed by governing bodies and customer awareness of adverse global warming effects have resulted in an accelerated move in automotive industry towards development of electric powertrains in response. However, refinement of issues related to electric vehicle noise, vibration, and harshness (NVH) attributes remain as a significant challenge in automotive powertrains industry [1]. In the absence of internal combustion (IC) engines, passengers perceive unwanted noises from transmission and auxiliary units. Gear vibrations during meshing generate an intrusive tonal noise known as gear whine [2]. Gear whine harmonics have the largest impact on the sound quality of electric powertrains [3].

Various palliative isolation techniques can be used to reduce gear noise, but sound proofing and noise cancellation are expensive and delicate. Hence, noise reduction at the source deems to be a more economical solution [4]. NVH in gear transmission systems has been investigated both theoretically and experimentally [5,6,7,8,9]. Internal and external dynamic excitations contribute to gear noise emissions. Dynamic excitations appear in the form of transmission error, mesh stiffness variations, friction forces, and bearing forces [8, 10]. Static transmission errors are due to geometrical irregularities and manufacturing errors. Backlash, time variable meshing stiffness and damping contribute to dynamic transmission error (DTE). An accurate prediction of gears’ dynamic response requires a detailed knowledge of these excitation sources. Palermo et al. [8] showed that DTE is the best quantitative indicator for gear NVH [8]. Blankenship and Kahraman [5, 11] proposed a detailed experimental study of DTE using a four-square spur gear test rig. Their findings are largely used in recent studies to develop detailed experimental investigations and theoretical gear models.

Several predictive tools have been developed with various levels of complexity to study gear dynamics [9, 12,13,14,15]. These models can be classified as full elastohydrodynamic (EHL) solvers and analytical models. EHL models detail gear contacts and associated tribology to study surface-lubricant interactions and gear contact losses due to friction. The simplest EHL model investigates isothermal non-Newtonian lubrication of gear contacts [16]. In a few studies, gear models include the surface deformations and asperity interactions in the mixed regime of lubrication [14]. The thermal effects on the contact tribology are investigated in more complicated gear models [17]. These tribological models are usually focussed on the contact and neglect the effect of global stiffness of gears on the mesh dynamics. Those EHL solvers are not often used in gear NVH studies due to their complexity and long simulation time. Gear noise analysis requires solution for multiple meshing cycles to include transient, nonlinear signatures in the dynamic response of gears. Hence, sophisticated analytical models can be a more economic and efficient approach, particularly in the system level dynamic analysis of electric vehicles.

The accuracy of analytical models primarily depends on their reliability in predicting time variable meshing stiffness (TVMS) of the gear pair. TVMS varies with contact load, number of teeth in contact, velocity, and radii of curvature of teeth along the line of action [14, 16]. Analytical and semi-analytical gear models conventionally estimate TVMS using one of the following methods: square wave fitted function, finite element method (FEM), boundary element method (BEM), experimental approximation, Weber’s method, the ISO standard, or the potential energy principle [6, 18,19,20,21]. The basic square wave TVMS only considers the variations between number of contacting teeth pair during the meshing cycle [18]. FEM-based TVMS is largely sensitive to contact tolerances, mesh density and type of elements. This method requires significantly greater computational time and power [22]. Experimental TVMS approximations are carried out using strain gauges and photoelasticity techniques [19, 23, 24]. However, the measurements are limited to static or low speed operating conditions. Potential energy method assumes that gear tooth is a non-uniform cantilever beam [21, 25,26,27,28,29]. Yang and Lin [29] included the bending and axial compression of the teeth pair in the potential energy TVMS. Tian et al. [30] adapted Yang and Lin’s model [29] and included the shear stiffness in TVMS. The effect of gear body deflection is neglected in those studies. Sainsot et al. [31] evaluated the tooth fillet-foundation deflection using a simple empirical formula to account for the tooth deflections induced by the gear body compliance. Other researchers adapted this model to determine the fillet-foundation stiffness [25, 27, 32,33,34]. A few studies combined the bending, axial, shear, and tooth fillet compliances in the prediction of the total TVMS [25, 27, 33]. Those analytical models were validated using finite element analysis (FEA). FEA results showed that the loading of neighbouring teeth during multiple teeth meshing can impose an additional deflection on the tooth through the gear body compliance [35,36,37]. Therefore, a correction factor was introduced based on FEM to modify the tooth fillet foundation stiffness. Xie et al. [38] proposed a comprehensive analytical approach to include the total gear body compliance effects. These analytical TVMS models consider either a linearised invariable pseudo-Hertz contact stiffness [25,26,27,28,29, 39, 40] or a nonlinear load-dependent contact stiffness based on empirical formulae [21, 35,36,37,38]. Guilbault et al. [6] used a boundary element method (BEM) to approximate TVMS. They combined the global stiffness with a load-dependent contact stiffness model based on Hertz line contact theory. Hertz contact model has also been applied to potential energy-based method in a recent study by Cao et al. [34].

Analytical methods study gear mesh stiffness and lubricant damping independently. Three types of damping are present in a gear system: (i) system damping from shaft and bearings, (ii) material hysteresis damping, and (iii) lubricant damping [6]. Lubricant damping varies with contact load, speed, lubricant’s rheological properties, film thickness and squeeze film effect. Analytical models use formulations based on either constant damping ratio or simplified solutions of Reynolds equation [6, 11, 32,33,34,35, 41,42,43,44,45]. Chen et al. [21] combined the analytical TVMS model with a damping coefficient which varied with the compressive deformations of the contacting teeth. However, the damping coefficient formulation depended on a series of experimentally measured constants. Özgüven investigated the effects of shaft and bearing dynamics on the gear meshing response using a constant lubricant damping ratio [41]. Parker et al. [42] used a similar constant damping ratio in their FEM-based TVMS model. These studies investigated contact stiffness and damping as two separate phenomena. The only connection between these elements is the contact load.

These analytical models are verified mainly using the experimental results in [5, 11]. The predicted DTEs in those models are in very good agreement with the measured DTEs. However, their TVMS models can noticeably differ from each other. An accurate analytical model should also represent the real physics of the problem whilst performing efficiently. Accurate prediction of physics in lubricated contacts is essential under extreme operating conditions, where lubricant load carrying behaviour will largely depend on the fast transitions between regimes of lubrication. Closed form solutions based on harmonic balance method (HBM) rely on mathematical Fourier series representation of meshing force harmonics. These models do not provide detailed insight into the tooth compliance, and neglect lubricant stiffness [11, 46]. A few models utilise fitted polynomial functions to describe TVMS. Those models require an extensive FEM or BEM simulations to initially determine the polynomial constants specific to each gear design [6, 15]. Some multibody dynamics (MBD) models assume the teeth and gear are rigid bodies, which are connected through a series of torsional springs at the teeth foundation [44]. The contact stiffness is predicted using Hertz contact theory. However, this stiffness model neglects contributions from teeth axial and shear deformations as well as the gear body compliances and lubricant elastic behaviour. The potential energy approach is advantageous because it describes teeth stiffness using exact analytical functions [34, 43]. These models utilise either a linearised Hertz contact stiffness model, or Weber formula for elastic line contact deformations. The highlighted analytical approaches neglect the lubricant stiffness under highly loaded gear contact conditions. 1D EHL solutions based on Reynolds equation account for piezo-viscous effects of lubricant [13]. However, those models require a numerical approach to solve the Reynolds equation and neglect global tooth and gear body compliances. None of these analytical approaches consider the TVMS with lubricant-surface interactions based on the transitions between the regimes of lubrication. Despite the good agreement between the available analytical models and measured DTE amplitudes, there seems to be a lack of a simple analytical model, which is representative of the real physics of gear teeth contacts and can provide more detailed insight into the root cause of gear whine noise. Once developed, such model can efficiently be adapted in system-level analysis of gear transmission systems.

Lubricant-surface interactions affect contact stiffness and damping proportionally. A study of regimes of lubrication shows that lubricant can behave akin to an amorphous solid under very high contact pressures that are often encountered in electric vehicle transmission systems [47,48,49]. Lubricant can undergo four fluid regimes of lubrication: (i) iso-viscous rigid (IR), (ii) piezo-viscous rigid (PR), (iii) iso-viscous elastic (IE) and (iv) piezo-viscous elastic (PE). Gear dynamics has a highly transient and nonlinear nature. Hence, multiple transitions are possible between these regimes of lubrication during a single meshing cycle. Film thickness varies with viscosity and elasticity parameters in each regime of lubrication [47,48,49,50,51,52]. Hence, a single Hertz contact model cannot accurately describe the contact stiffness. Full EHL solvers include these effects in the estimated film thickness [9, 13, 14, 16, 53].

In this research, a gear tribodynamics model is developed using potential energy TVMS method. A fully analytical model is proposed for lubricated contact stiffness based on transitions in the regimes of lubrication. The model accounts for both solid surface elasticity and lubricant compressive stiffness through a single lubricant-surface stiffness coefficient. Film thickness and damping coefficients are updated with the relevant film thickness at each instant during meshing cycle. The predicted TVMS is compared with the Hertz contact stiffness during a complete meshing cycle. Predicted DTE amplitudes are compared with both measured values and predicted results from Hertz contact model. Gear harmonic and super-harmonic resonances are investigated in terms of amplitude, frequencies and stiffness softening nonlinearities. The stability of the gear pair dynamics is scrutinised at the main harmonic and the second super-harmonic frequencies using time history responses and phase-displacement diagrams. The lubricated contact model has a better accuracy and is considerably time efficient in comparison to one-dimensional EHL solvers. The proposed model can be adapted to characterise gear NVH and diagnose system level NVH problems in electric vehicle powertrains.

2 Gear tribodynamics model

Detailed models provide a better understanding of the nonlinear gear inefficiencies and NVH problems. However, simpler but sufficiently accurate analytical models are more economic. A combined dynamics and tribological (tribodynamic) model of a gear mesh is developed using a more accurate analytical approach. The model accounts for the transmission error nonlinearities such as backlash, time variable meshing stiffness (TVMS) and lubricated contact variations based on the regime of lubrication at the teeth interface.

2.1 Gear dynamics

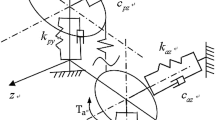
Figure 1 depicts a two degrees of freedom model of a spur gear system. The model comprises a detailed analysis of the gear meshing stiffness \({K}_{m}\) and damping \({C}_{m}\). Subscripts 1 and 2 refer to the input (driver) gear and output (driven) gear, respectively. \({T}_{1}\) and \({T}_{2}\) are the driving and resistive torques, respectively. Churning and friction losses are neglected for simplicity. Therefore, equations of motion for the gear dynamics can be written as:

$$\left\{\begin{array}{l}{I}_{1}{\ddot{\theta }}_{1}(t)+{R}_{1}\mathrm{cos}\varphi {F}_{\mathrm{dyn}}(t)={T}_{1}\\ {I}_{2}{\ddot{\theta }}_{2}(t)+{R}_{2}\mathrm{cos}\varphi {{z}_{g}F}_{\mathrm{dyn}}(t)={T}_{2}\end{array}\right.$$
(1)

where, \(I\), \(\theta \), \(R\) and \(\varphi \) are the gear mass moment of inertia, angular position, pitch radius and pressure angle, respectively. \({z}_{g}\) represents the gear speed ratio. The dynamic gear load, \({F}_{\mathrm{dyn}}\), varies with meshing stiffness and damping over time:

Fig. 1
figure 1

Schematic of the dynamic model developed for the spur gear pair

Full size image
$${F}_{\mathrm{dyn}}(t)={K}_{m}(t)\delta (t)+{C}_{m}(t)\dot{\delta }(t)$$
(2)

The time variable meshing stiffness \({K}_{m}\) and damping \({C}_{m}\) are nonlinear in time. \(\delta \) is dynamic transmission error (DTE):

$$\delta \left(t\right)=\left[{R}_{1}{\theta }_{1}(t)+{R}_{2}{\theta }_{2}(t)\right]\mathrm{cos}\varphi $$
(3)

2.2 Gear mesh stiffness

The potential energy approach is adapted in this model to describe the global tooth stiffness. The local contact stiffness is initially modelled using the Hertz line contact theory. A detailed stiffness model is introduced for lubricated gear contacts based on the regimes of lubrication. The results from this model are compared with Hertz contact model and measured results from literature.

TVMS varies with the local contact deformation and the global bending, shear, axial and tooth root (fillet foundation) deflections. The spur gear tooth is assumed as a non-uniform cantilever beam (Fig. 2). Therefore, the tooth pair stiffness \({K}_{t}\) can be determined based on the respective potential energy of each deflection component in gears 1 and 2 [25, 27]:

$$ \frac{1}{{K_{t} \left( t \right)}} = \frac{1}{{k_{c} \left( t \right)}} + \mathop \sum \limits_{i = 1}^{2} \left( {\frac{1}{{k_{b,i} }} + \frac{1}{{k_{a,i} }} + \frac{1}{{k_{s,i} }} + \frac{1}{{k_{f,i} }}} \right) $$
(4)

where, \({k}_{c}\), \({k}_{b}\), \({k}_{a}\), \({k}_{s}\) and \({k}_{f}\) represent contact, bending, axial, shear, and fillet foundation stiffness components, respectively. The subscript \(i\) indicates the gear number. These components are described using gear geometric parameters in Fig. 2 [28]:

$$ \frac{1}{{k_{a} }} = \mathop \int \limits_{{ - \alpha_{1} }}^{{\alpha_{2} }} \frac{{R_{b} \sin^{2} \left( {\alpha_{1} } \right)\left( {\alpha_{2} - \alpha } \right)\cos \left( \alpha \right)}}{{EA_{x} }}{\text{d}}\alpha $$
(5)
$$ \frac{1}{{k_{s} }} = \mathop \int \limits_{{ - \alpha_{1} }}^{{\alpha_{2} }} \frac{{2.4R_{b} \left( {1 + \nu } \right)\cos^{2} \left( {\alpha_{1} } \right)\left( {\alpha_{2} - \alpha } \right)\cos \left( \alpha \right)}}{{EA_{x} }}{\text{d}}\alpha $$
(6)
$$ \frac{1}{{k_{b} }} = \mathop \int \limits_{{ - \alpha_{1} }}^{{\alpha_{2} }} \frac{{R_{b}^{3} \left[ {1 + \cos \alpha_{1} \left\{ {\left( {\alpha_{2} - \alpha } \right)\sin \alpha - \cos \alpha } \right\}} \right]^{3} \left( {\alpha_{2} - \alpha } \right)\cos \left( \alpha \right)}}{{EI_{x} }}d\alpha $$
(7)

where, \({R}_{b}\), \(L\),\(E\) and \(\nu \) are the radius of base circle, tooth face width, Young’s modulus of elasticity and Poisson’s ratio, respectively. The cross-sectional area of tooth at distance \(x\) from the tooth base is \({A}_{x}=2{h}_{x}L\) and the second moment of area of tooth is \({I}_{x}=\frac{2}{3}{h}_{x}^{3}L\). The distance from tooth centreline to tooth surface, \({h}_{x}\), is shown in Fig. 2a and equals \({R}_{b}[\left({\alpha }_{2}-{\alpha }_{1}\right)\mathrm{cos}\alpha +\mathrm{sin}\alpha ]\). This study focuses on the effects of lubricant-surface interactions in predicting TVMS and the overall nonlinear dynamics response of the gear system. Therefore, the analytical formulation for the fillet-foundation stiffness in [31] is used based on the research carried out in [25, 27, 32,33,34]. The more comprehensive approach in [38] can be adapted in future to account for the gear body compliance coupling with its neighbouring teeth.

Fig. 2
figure 2

Gear tooth geometric parameters for calculation of a tooth stiffness as a non-uniform cantilever beam, and b tooth fillet foundation stiffness

Full size image
$$\frac{1}{{k}_{f}}=\frac{{\mathrm{cos}}^{2}{(\alpha }_{1})}{EL}\left\{{L}^{*}{\left(\frac{{u}_{f}}{{S}_{f}}\right)}^{2}+{M}^{*}\left(\frac{{u}_{f}}{{S}_{f}}\right)+{P}^{*}(1+{Q}^{*}{\mathrm{tan}}^{2}\left({\alpha }_{1}\right))\right\}$$
(8)

Parameters \({L}^{*}\), \({M}^{*}\), \({P}^{*}\), and \({Q}^{*}\) depend on gear geometrical parameters such as ratio between gear root radius and hub radius, number of teeth, cutter tool tip radius, the pressure angle, and the tooth addendum [31]. The geometrical parameters \({u}_{f}\) and \({S}_{f}\) are illustrated in Fig. 2b.

The number of pair of teeth in contact, \(n\), varies along the line of contact and depends on the contact ratio. Therefore, the total mesh stiffness is calculated using the instantaneous value of \(n\) along the line of contact:

$$ \frac{1}{{K_{m} \left( t \right)}} = \mathop \sum \limits_{j = 1}^{n} \left( {\frac{1}{{K_{t,j} \left( t \right)}}} \right) $$
(9)

2.2.1 Hertz contact stiffness

The pseudo-Hertz contact stiffness is \({k}_{\mathrm{ph}}=\pi \mathrm{EL}/(4\left(1-{\nu }^{2}\right))\). This model has been largely adapted in the energy-based TVMS [25,26,27,28, 32]. In this model, \(E\) is the Young’s modulus of elasticity. However, Hertz line contact model depends on contact load \({F}_{\mathrm{dyn}}\) and half contact footprint width \(b\). Therefore, gear teeth conjunction is assumed as two cylindrical bodies in contact. The elastic deflection \(\sigma \) for each gear surface is described as [6, 54]:

$$\left\{\begin{array}{c}{\sigma }_{1}(t)=\left(\frac{{F}_{\mathrm{dyn}}}{L}\right)\left(\frac{1-{\upsilon }_{1}^{2}}{\pi {E}_{1}}\right)\left\{2\mathrm{ln}\left(\frac{4{\rho }_{c1}}{b}\right)-1\right\}\\ {\sigma }_{2}(t)=\left(\frac{{F}_{\mathrm{dyn}}}{L}\right)\left(\frac{1-{\upsilon }_{2}^{2}}{\pi {E}_{2}}\right)\left\{2\mathrm{ln}\left(\frac{4{\rho }_{c2}}{b}\right)-1\right\}\end{array}\right.$$
(10)

where, half contact width is \(b=\sqrt{8{F}_{\mathrm{dyn}}{\rho }_{\mathrm{eq}}/\pi {\mathrm{LE}}^{\mathrm{^{\prime}}}}\) and the equivalent radius of curvature of the two contacting surfaces is \({\rho }_{\mathrm{eq}}=({\rho }_{c1}+{\rho }_{c2})/{\rho }_{c1}{\rho }_{c2}\). \({\rho }_{c}\) is the radius of curvature of gear tooth profile. The reduced modulus of elasticity \({E}^{^{\prime}}\) is given by \({E}^{^{\prime}}=2/\left(\frac{1-{v}_{1}^{2}}{{E}_{1}}+\frac{1-{v}_{2}^{2}}{{E}_{2}}\right)\) [14, 47]. Hence, the Hertz contact stiffness, \({k}_{h}\), is given as:

$${k}_{h}(t)=\frac{{F}_{\mathrm{dyn}}(t)}{{\sigma }_{1}(t)+{\sigma }_{2}(t)}$$
(11)

During the elastic teeth contact, contact stiffness \({k}_{c}={k}_{h}\) in Eq. (4). TVMS with Hertz contact model neglects lubricant stiffness. Hence, \(1/{k}_{c}=0\) during teeth separation. The transition between these two conditions is conventionally established using a lubricant film thickness limit. This lower film limit is determined based on the solution of a single degree of freedom gear impact problem under low pressure iso-viscous conditions [55] or simply through the lubricant damping force balance between contact and no-contact conditions [6].

2.2.2 Lubricated contact stiffness

Tribological contacts undergo a more complicated physics than assuming a simple lower film limit condition. In reality, the lower film limit varies with contact load, entrainment velocity and the rheological properties of lubricant. Therefore, contact might undergo multiple transitions based on the regime of lubrication and the contact stiffness varies with those regimes. Various researchers have attempted slightly different formulations to determine the transition boundaries for those regimes of lubrication [47,48,49, 56, 57]. Hooke’s chart is adapted to the line contact problem in this study [47]. The four regimes of lubrication can be described using the dimensionless viscosity and elasticity parameters, \({g}_{v}\) and \({g}_{e}\) respectively [47]:

$$\left\{\begin{array}{c}{g}_{v}={\left(\frac{{{\alpha }^{*}}^{2}{F}_{\mathrm{dyn}}^{3}(t)}{{\eta }_{\mathrm{o}}\overline{V}{\rho }_{\mathrm{eq}}^{2}{L}^{3}}\right)}^{1/2}\\ {g}_{e}={\left(\frac{{F}_{\mathrm{dyn}}^{2}(t)}{{\eta }_{\mathrm{o}}\overline{V}{E }^{\mathrm{^{\prime}}}{\rho }_{\mathrm{eq}}{L}^{2}}\right)}^{1/2}\end{array}\right.$$
(12)

The pressure-viscosity coefficient \({\alpha }^{*}\) in Eq. (13) is defined as [58]:

$${\alpha }^{*}=\frac{1}{p}\left(\mathrm{ln}{\eta }_{\mathrm{o}}+9.67\right)\left[{\left(\frac{{T}_{\mathrm{lub}}-138}{{T}_{\mathrm{amb}}-138}\right)}^{{S}_{0}}{\left(1+5.1\times {10}^{-9}p\right)}^{{Z}_{o}}-1\right]$$
(13)

where, \({S}_{0}\) and \({Z}_{o}\) are Roeland’s thermo-viscous and piezo-viscosity constants, respectively. The bulk temperature of lubricant \({T}_{\mathrm{lub}}\) is invariable and, the thermo-viscous term adjusts the lubricant viscosity with respect to the reference temperature at ambient pressure. Here, \({T}_{\mathrm{amb}}\) is ambient temperature. \({\eta }_{o}\) is the dynamic viscosity of lubricant at ambient temperature and pressure. \(\overline{V }\) describes the entrainment velocity of the lubricant in the direction of the line of contact. The dimensionless viscosity and elasticity parameters in Eq. (12) can be used to evaluate the dimensionless minimum film thickness, \(\overline{h }\), for each regime of lubrication (Table 1). The minimum film thickness, \({h}_{o}\), is calculated as:

Table 1 Dimensionless film thickness boundaries and lubricated contact stiffness for the four regimes of lubrication
Full size table
$$\overline{h }=\frac{{h}_{\mathrm{o}}{F}_{\mathrm{dyn}}(t)}{{\eta }_{\mathrm{o}}{\rho }_{\mathrm{eq}}\overline{V}L }$$
(14)

Table 1 presents the lubricated contact stiffness using Hooke’s law analogy (\({k}_{lc}=\mathrm{d}{F}_{\mathrm{dyn}}/\mathrm{d}{h}_{o}\)). Lubricant stiffness is noticeably smaller in iso-viscous rigid (IR) regime of lubrication. Hence, it is neglected in the current study. Film thickness in piezo-viscous rigid (PR) regime of lubrication is invariable with the dimensionless elasticity parameter \({g}_{e}\). Therefore, the main contribution to contact stiffness originates from the lubricant. Contact stiffness largely depends on solid’s elasticity in iso-viscous elastic (IE) regime. This regime is also known as soft elastohydrodynamic lubrication (EHL). Contact undergoes hard EHL in piezo-viscous elastic regime of lubrication, where lubricant stiffness is comparable to the stiffness of the elastic surfaces. The contact stiffness, \({k}_{c}\), in Eq. (4) is updated based on the regime of lubrication at each simulation time step in the gear tribodynamics model. The performance of lubricated contact stiffness model will be compared with Hertz contact model and experimentally measured DTE amplitudes in the results section.

2.3 Mesh damping

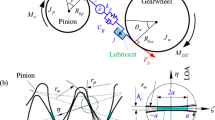
Figure 3 shows lubricant film entrained into the gear mesh conjunction. A simplified damping model is adapted based on the solution of Reynolds equations [6]. A uniform pressure distribution is assumed in ‘z’ direction for the gear line contact (i.e. \(\partial p/\partial z=0\)). Side leakage in ‘z’ direction and wedge effects in ‘y’ direction are neglected. Hence, a 1D Reynolds equation describes the Poiseuille pressure in ‘y’ direction and squeeze behaviour of the lubricant in time.

Fig. 3
figure 3

Trapped lubricant between teeth flanks in contact

Full size image
$$\frac{\partial }{\partial y}\left(\frac{{h}^{3}}{\eta }\frac{\partial p}{\partial y}\right)=12\frac{\partial h}{\partial t}$$
(15)

Guilbault et al. [6] have applied the viscous damping analogy to the solution of Reynolds Eq. (15) to describe an equivalent damping coefficient for rigid (no-contact) and elastic (contact) conditions. For rigid (no-contact) condition, the film thickness is approximated by \(h\left(y\right)={h}_{o}+{y}^{2}/2{R}_{\mathrm{eq}}\). Reynolds Eq. (15) is solved with \(p\left(y\right)=0\) at \(y=\pm a\) boundary conditions. The virtual contact half-width, \(a\), is defined as the shortest distance between the virtual contact radius, \({r}_{c}\), and the tip radius, \({R}_{t}\), of the teeth in contact [6]. Therefore, the modified Guilbault et al. [6] damping coefficient for rigid (no-contact) condition will be:

$${C}_{\mathrm{nc}}=6\eta L\left[\sqrt{2{\left(\frac{{\rho }_{\mathrm{eq}}}{{h}_{\mathrm{o}}}\right)}^{3}}{\mathrm{tan}}^{-1}\left(\frac{a}{\sqrt{2{\rho }_{\mathrm{eq}}{h}_{o}}}\right)+2\frac{{\rho }_{\mathrm{eq}}^{2}a\left({a}^{2}-2{\rho }_{\mathrm{eq}}{h}_{o}\right)}{{h}_{o}{\left({a}^{2}+2{\rho }_{\mathrm{eq}}{h}_{o}\right)}^{2}}\right]$$
(16)

Here \(\eta \) is adjusted to account for temperature effects, and piezo-viscous effects are considered to be negligible under no contact condition. The film thickness is largely invariable inside the contact footprint. Hence, film thickness is assumed as \(h={h}_{o}\) in contact [60]. Boundary condition \(p\left(y\right)=0\) is applied at Hertz half contact width limits \(y=\pm b\) [6]. Therefore, damping coefficient for elastic (contact) condition is:

$${C}_{c}(t)=\frac{8\eta {b}^{3}(t)L}{{h}_{0}^{3}}$$
(17)

Transition between these damping coefficients is based on a lower film thickness limit using DTE values. Guilbault et al. [6] evaluate the dynamic viscosity of lubricant using Houpert’s formulation:

$$\eta ={\eta }_{0}\mathrm{exp}\left({\alpha }^{*}p\right)$$
(18)

The damping coefficient formulation in [10] is adapted for the current gear tribodynamics model. The mesh damping nonlinearly varies with time due to the fluctuations in the number of teeth in contact, dynamic loading, and contact damping coefficients. Structural damping \({C}_{\mathrm{st}}\) and external system damping \({C}_{\mathrm{sys}}\) are estimated using constant damping ratios \({\zeta }_{\mathrm{st}}=0.33\%\) and \({\zeta }_{\mathrm{sys}}=0.5\%\), respectively [6].

$${\zeta }_{i}=\frac{{C}_{i}}{2\sqrt{{\overline{K} }_{m}{m}_{e}}}$$
(19)
$${m}_{e}=\frac{{I}_{1}{I}_{2}}{{I}_{1}{R}_{b2}^{2}+{I}_{2}{R}_{b1}^{2}}$$
(20)

where, \(i\in \{\mathrm{st},\mathrm{sys}\}\) in Eq. (19) and \({m}_{e}\) is the equivalent mass. \({\overline{K} }_{m}\), \(I\) and \({R}_{b}\) are the average meshing stiffness, mass moment of inertia of gear and base circle radius, respectively. Gear mesh damping can be evaluated using:

$$ C_{m} \left( t \right) = C_{{{\text{sys}}}} + \mathop \sum \limits_{j = 1}^{n} \left( {\frac{1}{{C_{{{\text{st}}}} }} + \frac{1}{{C_{{{\text{lub}}}} \left( t \right)}}} \right)_{j}^{ - 1} $$
(21)

where, \({C}_{\mathrm{lub}}\) is determined using Eqs. (16) and (17) depending on the contact conditions (contact or no-contact) and \(n\) is the instantaneous number of teeth pair in contact along the line of contact.

2.4 Contact conditions

Contact conditions change due to dynamic nature of gear mesh. Gear teeth flanks can approach or separate inside the gear teeth backlash. These contact discontinuities impose an additional nonlinearity in TVMS and mesh damping. Therefore, the dynamic response of the gear mesh will extremely be transient and nonlinear. The normal approach of flanks, \(\epsilon \), is described as:

$$\epsilon =\left({R}_{1}{\theta }_{1}+{R}_{2}{\theta }_{2}\right)\mathrm{cos}\varphi $$
(22)

The total backlash equals \(2B\). The relative position of teeth inside backlash defines direction of TVMS and mesh damping forces. Therefore, four contact conditions can be described for the Hertz contact model during a complete meshing cycle [6]:

  1. (a)

    \(\epsilon \ge 0\): front flanks are in contact, and lubricant is trapped in this conjunction.

  2. (b)

    \(-B\mathrm{cos}\varphi \le \epsilon <0\): teeth flanks are separated but located at the frontal half of backlash. Mesh stiffness \({K}_{m}(t)=0\) and lubricant damping \({C}_{\mathrm{lub}}(t)\) are included between the front flanks.

  3. (c)

    \(-2B\mathrm{cos}\varphi <\epsilon <-B\mathrm{cos}\varphi \): teeth flanks are separated but located at the rear half of backlash. Mesh stiffness \({K}_{m}(t)=0\) and lubricant damping \({C}_{\mathrm{lub}}\) are included between the back flanks.

  4. d)

    \(\epsilon \le -2B\mathrm{cos}\varphi \): back flanks are in contact, and lubricant is trapped in this conjunction. Therefore, both \({K}_{m}(t)\) and mesh damping \({C}_{m}(t)\) are included between the back flanks.

Lubricant carries load during film squeeze. This load carrying capacity deteriorates during film tension. Therefore, lubricant damping \({C}_{\mathrm{lub}}=0\) during separation at either the front or back flanks. These four conditions are described for a Hertz contact model. In the lubricated contact model, the same intervals determine the tooth position inside backlash. However, mesh stiffness and damping coefficients are determined through lubrication regime map. The transition between contact and no-contact conditions is specified based on the film limits at the boundaries of those lubrication regimes. Thus, the lubricated contact model provides a detailed physical description of gear tribodynamics. The proposed analytical approach allows for more complicated simulations pertaining to real world applications whilst less resources are consumed. Such detailed analytical model has not hitherto been reported in the literature.

3 Results and discussion

3.1 Validation of lubricated contact model

A series of simulations were carried out using both the proposed lubricated contact model specifically developed in this study and the conventional Hertz model. Blankenship and Kahraman [5] precisely measured the DTE for a range of speeds and torques using a lubricated four-square test rig. They reported an average two-percent system damping regardless of torque and speed variations [5]. The predicted DTE amplitudes are compared with these measured DTE amplitudes later on. Spur gear pairs undergo a highly transient and nonlinear tribodynamics response. Analytical models allow prediction of gear mesh resonance and study of DTE harmonics above and below the main resonance response. The analytical mesh stiffness and damping models are combined with the numerical solution of dynamics model in this study. Runge–Kutta predictive-corrective approach is used to solve dynamics equations of motion. The flow chart in Fig. 4 shows the iterative solution method of the tribodynamics model developed in this study and the associated equations of motion. Gear system specifications of Blankenship and Kahraman [5] are used in the validation simulations (Table 2). Identical gears are used in the measured DTE results.

Fig. 4
figure 4

Flow chart for the developed tribodynamics model

Full size image
Table 2 Geometrical, mechanical, and rheological specifications of the gear-lubricant system [5, 6]
Full size table

Figure 5 shows the predicted and measured root-mean-square of DTE amplitudes at 100 Nm torque. The gear meshing frequency is varied between 0.6 kHz and 3.5 kHz. The measured results show a gear harmonic frequency about 2.35 kHz. Hertz and lubricated contact models predict the gear harmonic frequency at 2 kHz and 2.25 kHz, respectively. The measured DTE amplitude at this frequency is about 7.5 µm and the predicted amplitudes are about 8 µm for lubricated and 12 µm for Hertz contact models. Lubricated contact model shows a better agreement with the measured DTE between 1.5 and 3.5 kHz. Measured DTE shows three super-harmonic resonances at about 0.7, 0.9 and 1.3 kHz. DTE excitations have direct correlation with gear system vibration [8] and higher gear whine noise is anticipated near these meshing frequencies. Predicted DTE amplitudes plateau near these super-harmonics for Hertz contact model. Lubricated contact model slightly overestimates the DTE amplitudes but accurately predicts these super-harmonic frequencies. The softening stiffness nonlinearity can be observed in the measured DTE amplitudes at the gear harmonic 2.35 kHz and the first super-harmonic 1.3 kHz. The second (0.9 kHz) and third (0.7 kHz) super-harmonics show a mild nonlinearity. The developed lubricated contact model is clearly more successful in predicting DTE amplitudes, harmonic frequencies and the stiffness softening behaviour. Therefore, accurate prediction of contact stiffness based on regimes of lubrication has a paramount importance for system dynamic analysis. The performance of lubricated contact model is thus, verified using experimentally measured DTE amplitudes in Fig. 5. The proposed analytical model has a very good agreement with the measured results. It is also cost-effective and time efficient in comparison to detailed numerical EHL models.

Fig. 5
figure 5

Comparison of predicted DTE amplitudes from Hertz and lubricated contact stiffness models with measured DTE amplitudes from [5] at 100 Nm

Full size image

3.2 Lubricated TVMS characterisation

Dynamic transmission error (DTE) is the main root cause of gear whine noise. This transmission error is affected by various static and dynamic parameters including backlash, manufacturing errors, variable meshing stiffness, lubrication behaviour and other external factors. Thus, a detailed characterisation of the lubricated TVMS is required to better understand the DTE performance in Fig. 5.

Hertz contact model uses a single contact stiffness formulation, whilst the contact stiffness in the developed lubricated contact model varies with the regime of lubrication. These transitions are included in the gear model based on the boundaries of lubrication regime chart (Fig. 6). The gear tribodynamics is simulated at both low torque (100 Nm) and high torque (300 Nm) loading conditions. These torques are selected based on the measured results in the literature [4]. Dimensionless viscosity, \({g}_{v}\), and elasticity, \({g}_{e}\), parameters are evaluated at low (0.6 kHz), gear super-harmonic (1.15 kHz) and high (3.5 kHz) meshing frequencies. Gear system undergoes iso-viscous rigid (IR) regime of lubrication at lower loads and higher speeds (Fig. 6). A transition to higher load and lower speeds will impose piezo-viscous rigid (PR) and piezo-viscous elastic (PE) regimes of lubrication. At super-harmonic frequency, lightly loaded gear teeth predominantly remain in iso-viscous rigid (IR) regime, whereas regime of lubrication is dominantly piezo-viscous elastic (PE) at 300 Nm. This indicates the highly transient and nonlinear nature of gear contact. Hence, accurate prediction of contact stiffness is prerequisite to reliable evaluation of DTE amplitudes at gear harmonics. Gear mesh systems barely experience iso-viscous elastic (IE) regime due to the relatively high modulus of elasticity of steel material. The lubricated contact stiffness is negligible in the IR region. Hence, PR and PE stiffness equations (Table 1) contribute to the simulations.

Fig. 6
figure 6

Regimes of lubrication chart created for six different cases of operating conditions. Lubricant regime chart constructed using Hooke's charting procedure [47]

Full size image

TVMS variations for Hertz and lubricated contact models are presented in gear roll angle domain during a complete meshing cycle (Fig. 7). These contact models are combined with the potential energy approach. Experimental measurement of TVMS in dynamic gear system is not straightforward. Therefore, the reported TVMS results from literature based on boundary elements method and Hertz contact (BEM-Hertz) model [6] are used as benchmark for comparison. Gear contact ratio is 1.75 and steps in TVMS represent transition between single and double teeth contact. Gear teeth predominantly operate in PR and PE regimes of lubrication as shown in Fig. 6. Therefore, TVMS is evaluated at representative torques and meshing frequencies for those regions in Fig. 7: (a) 3.5 kHz and 100 Nm in piezo-viscous rigid (PR) and (b) 0.6 kHz and 300 Nm in piezo-viscous elastic (PE) regimes of lubrication. Meshing stiffness for Hertz contact model remains largely invariable in both scenarios and noticeably below the BEM-Hertz stiffness (Fig. 7a, b). The Hertz stiffness only varies with contact radius of curvature, load, and footprint size (Eqs. (10) and (11)). The lubricated contact model predicts greater stiffness values in comparison with Hertz stiffness model in both cases. Greater stiffness values in the lubricated model are associated with the compressive stiffness and damping of lubricant in PR regime of lubrication. Lubricated stiffness is in a very good agreement with BEM-Hertz results. A greater TVMS is observed for lubricated model after the transition from PR to PE regime of lubrication due to the effects of viscosity and elasticity through \({g}_{v}\) and \({g}_{e}\) parameters (Fig. 7b). This increase in TVMS is associated with the variations in gear operating conditions. Lower speeds and greater loads during PE regime of lubrication cause a noticeable rise in lubricant viscosity. Therefore, lubricant can behave like an amorphous solid, where its stiffness can rise to values comparable to those of its contiguous solids [60]. The BEM-Hertz model neglects the lubricant stiffness and underpredicts the overall TVMS. Hence, the lubricant-surface interactions are significant in the prediction of TVMS.

Fig. 7
figure 7

Comparison of the Hertz and lubricated TVMS models in potential energy approach with BEM-Hertz model [6] at a piezo-viscous rigid (3.5 kHz and 100 Nm) and b piezo-viscous elastic (0.6 kHz and 300 Nm) regimes of fluid film lubrication

Full size image

3.3 Analysis of DTE time and phase responses

When studying gear transmission NVH, the dynamic characteristics are described using the harmonics in the signature. Gear meshing harmonics can be associated with gear whine noise. In analytical approaches, those harmonics are quantified using DTE amplitudes and frequencies. Time history and phase-displacement representation of DTE signature can provide detailed information as to how those harmonics interact and correlate with the physical events during gear meshing events such as in gear teeth separations, back-side impacts inside backlash, variations in lubricated contact conditions, etc. A detailed comparison of Hertz and lubricated contact models is provided for the gear pair model. The system behaviour is studied in the vicinity of the main harmonic (2.35 kHz) and 2nd super-harmonic (0.9 kHz) resonances. Figure 8a, b presents DTE time responses immediately before and after the 2nd super-harmonic resonance. The time response is more stable before resonance and lubricated contact model clearly shows one main oscillation followed by two smaller amplitudes associated with the 1/3rd order of main harmonic. DTE amplitudes are noticeably larger and more chaotic after resonance. The higher negative DTE values and chaotic behaviour indicate larger tendency towards contact losses. DTE values remain within the backlash limit. Therefore, meshing is unlikely to undergo back-side contacts despite teeth separations. Hertz contact model overestimates the amplitudes before resonance. Phase-displacement trajectories show two stability foci before resonance (Fig. 9a). The stability focus in negative DTE direction is associated with the oscillations at the main harmonic frequency during teeth separation. The stability focus in the positive DTE direction represents oscillations at the 2nd super-harmonic resonance. Oscillation limit cycles shift between these foci at the saddle points on the trajectories. These saddle points appear about 0 µm DTE close to the contact threshold between surfaces. After resonance, the stability foci become more concentric in the lubricated contact model (Fig. 9b). Hertz contact model, however, indicates two distinctive stability foci after resonance. Figure 8c, d shows the transition to a single harmonic wave associated with the main resonance frequency. DTE amplitudes are larger at this frequency. The performance of Hertz contact model improves near the main resonance frequency. Phase-displacement trajectories comply with the observations from the time response (Fig. 9c, d). More concentric stability foci dominantly exist in the diagrams. Before resonance, the centres of the dominant limit cycles are inclined towards negative DTE values, i.e. possibility of gear teeth separation. A smaller limit cycle in the proximity of the positive DTE values represents the troughs in the time response before the resonance (Fig. 9c).

Fig. 8
figure 8

DTE response in time at 100 Nm torque and various speeds: a 0.85 kHz before the 2nd super-harmonic resonance, b 0.965 kHz after the 2nd super-harmonic resonance, c 1.9 kHz (2280 RPM) before the main gear harmonic, and d 2.3 kHz (2760 RPM) after the main gear harmonic

Full size image
Fig. 9
figure 9

Phase-plane plot at 100 Nm torque and various speeds: a 0.85 kHz mesh frequency before the 2nd super-harmonic resonance, b 0.965 kHz mesh frequency after the 2nd super-harmonic resonance, c 1.9 kHz mesh frequency before the main gear harmonic, and d 2.3 kHz mesh frequency after the main gear harmonic

Full size image

3.4 Model accuracy and performance

The lubricated contact model presented in this study can identify the main harmonic and super-harmonic frequencies in time response and phase-displacement domains. Detailed study of DTE proves the robustness of predicted dynamic responses. However, the precision of the analytical stiffness formulations is yet to be examined. Numerical models based on finite difference methods are conventionally used to predict lubricant pressure distributions as well as the shape of the distorted geometry under EHL regime [9, 14]. Sivayogan et al. [62] developed a one-dimensional (1D) EHL solver with the capability to identify transitions between Newtonian and non-Newtonian lubrication regimes. Accurate predictions of film thickness are important particularly in PE regime of lubrication. A minute difference in film thickness causes a large variation in contact stiffness in EHL contacts. Therefore, the EHL solver reported in [62] is used to assess the pressure and film distributions at various locations along the line of contact at 600 Hz meshing frequency and 300 Nm load (Fig. 10). The predicted minimum film thickness values are compared between the EHL solver and the analytical model (Table 3). The proposed analytical model has a very good agreement with the numerical EHL solver. However, the analytical model is cost-effective and time efficient in comparison with detailed numerical EHL models. Simulations were carried out on a machine with a Core-i5, 4.70 GHz processor. The EHL solver took 5 h CPU time to complete simulations for 20 contact points along the line of contact. Analytical model consumed only 6 min CPU time to complete the same simulations. Hence, analytical model provides reasonably accurate predictions with significantly less resources and cost.

Fig. 10
figure 10

One-dimensional elastohydrodynamic (EHL) results at various locations along the line of contact (LOC) at 600 Hz mesh frequency and 300 Nm: a lubricant pressure distributions and b the contact profile

Full size image
Table 3 Comparison of predicted minimum film thickness between the 1D EHL solver and the analytical lubricated contact model
Full size table

3.5 Dynamic performance map for EV operating conditions

Gear whine is the most common transmission noise in EVs and is correlated to DTE [7, 8]. Hence, an accurate determination of TVMS is important for the root cause analysis of gear whine noise. Dynamic performance map can demonstrate the generic trends in DTE and identify the gear vibration hotspots. The electric motor performance curves can be correlated with those critical vibration hotspots to qualitatively identify the critical operating conditions related to gear whine noise. The lubricated stiffness model in this study highlights the significance of the lubricant-surface interactions in the prediction of TVMS and the nonlinear DTE response. Thus, a series of simulations were carried out using the lubricated TVMS model for spur gear pair under the EV operating conditions. Electric motors for EV applications can typically reach 12,000 RPM speed and 450 Nm torque [63, 64]. Therefore, the equivalent meshing frequency and torque are varied up to 9.5 kHz and 500 Nm, respectively. Figure 11 shows the dynamic performance map of the rms DTE response for the studied spur gear pair. The same harmonic and subharmonic frequencies as those in Fig. 5 appear in the contour map. DTE amplitudes increase with the rise in the torque. Two main vibration hotspots are identified around 2.2 and 4.3 kHz meshing frequencies. These resonance hotspots spread over a larger meshing frequency domain at higher torque values. The higher DTE amplitudes can be associated with potentially more severe gear whine noise [7, 8]. Those operating conditions are mainly imposed by the electric motor speed and torque. Therefore, the motor performance (torque) curves are overlayed on the dynamic performance map (Fig. 11). The torque performance data is provided for an HVH250 series electric motor by BorgWarner [64]. These electric motor series are utilised in integrated electric drive modules for fully electric transmission drives. Motor RPM is converted to gear meshing frequency using the number of gear teeth in the meshing contact. Peak and continuous voltage curves represent the peak and continuous torque applied by the electric motor, respectively. Peak torque defines the instantaneous maximum torque typically delivered during the EV acceleration. Continuous torque is generated over longer period of steady-state operation. A sudden torque surge in electric motor can cause noticeably higher DTE amplitudes. Therefore, the powertrain is more likely to operate in resonance hotspots across a larger meshing frequency domain. Provided the EV operates under the steadier continuous torques, both DTE amplitudes and resonance frequency window reduce. Therefore, potentially higher gear whine levels are anticipated during acceleration maneuverers. The current simulations were run for the gear set in [5, 6, 11]. A more accurate correlation can be established using the actual gear specifications for an electric powertrain system. Despite the need for detailed system specifications, the proposed analytical approach can potentially identify the vibration hotspots in the component level gear system and correlate those with electric motor operating conditions for qualitative prediction of electric powertrain NVH responses. A more quantitative analysis of gear whine noise can, therefore, be established based on the methodology provided in this study.

Fig. 11
figure 11

Performance graphs of a typical EV motor [64] overlayed on the predicted DTE for the studied spur gear pair system for the prediction of DTE amplitudes at EV operating conditions

Full size image

4 Conclusion

Gear vibrations during mesh contacts generate the intrusive gear whine noise. This is of particular concern for electric vehicle manufacturers. Dynamic transmission error is the immediate root cause of gear whine. Fast but accurate gear models are fundamental for accurate prediction of dynamic transmission error for automotive powertrain designer and manufacturers. Full EHL numerical solvers are often used in the literature for accurate prediction of gear system tribodynamics. These detailed models, however, are resource intensive and incur higher computational time and costs. Analytical models, on the other hand, are simpler and cost-effective to run and maintain. Conventionally, time-varying meshing stiffness (TVMS) of gear mesh is predicted using Hertz contact theory. Those analytical models include contact elasticity and lubricant damping separately. However, elastic deformations of surface impose hysteretic damping and compression of lubricant at high pressures, which can make it behave similar to an amorphous solid, restores potential energy during the contact. In real applications, the gear contact can experience four different regimes of fluid film lubrication. In this study, a lubricated contact model is developed to account for contact stiffness variations with these regimes of lubrication. The lubricated contact model produces a better agreement with the measured results in the literature in comparison to conventional models. The following specific conclusions are achieved based on the presented results:

  1. 1.

    An accurate prediction of contact stiffness based on regimes of lubrication is prerequisite to reliable evaluation of dynamic transmission error. TVMS of Hertz contact model is largely invariable across different regimes of lubrication whilst the developed lubricated contact TVMS clearly shows the contribution of lubricant stiffness in comparison to the Hertz TVMS and across different regimes of lubrication.

  2. 2.

    The lubricated contact model in conjunction with the potential energy approach provides a more accurate prediction of harmonic and super-harmonic resonance amplitudes and frequencies. Hertz contact model has a reasonable performance at the main gear harmonic, but its performance deteriorates at super-harmonic resonance frequencies. The more comprehensive analytical model for fillet foundation stiffness in [38] can be adapted to further improve the accuracy of the lubricated contact model.

  3. 3.

    The lubricated contact model is able to show similar nonlinear stiffness softening trends to the measured DTE amplitudes. Time history and phase displacement analyses show nonlinear trends in DTE near the main harmonic and second super-harmonic. Two sources of nonlinearity can be identified using time and phase responses: (i) separation inside backlash imposes eccentric limit cycles, and (ii) lubrication regime impacts the position and amplitude of the limit cycles in the phase-displacement domain. Hence, an accurate contact model is essential for detailed analysis of gear meshing harmonics.

  4. 4.

    Time and phase responses can be combined with DTE amplitudes analysis to form a clearer understanding of the gear events, their correlations with DTE and contributions to gear whine signature.

  5. 5.

    Accuracy of the predictions from the developed analytical model for lubricated contact in this study is comparable with those from one-dimensional EHL solver. The model is significantly time efficient, which also makes it suitable to be used in higher system level dynamic models particularly for electric vehicle applications. A dynamic performance map based on the proposed analytical model can identify the DTE vibration hotspots and correlate those to the electric motor performance curves. The combined map of motor torque-speed curves and DTE amplitudes can showcase the potential operating conditions leading to the gear whine noise. A detailed analytical contact model with such accuracy and simulation time efficiency has not hitherto been reported in the literature.