Geometrically nonlinear dynamic analysis of the stiffened perovskite solar cell subjected to biaxial velocity impacts

Abstract

The perovskite solar cell (PSC) is one of the most promising photovoltaic candidates along with the highly increasing demand for green electricity. One of the main concerns regarding the PSC during its service life is nonlinear instability due to ultra-thin structural features and dynamic loadings. This paper presents a framework for nonlinear dynamic and stability analyses of the PSC with oblique stiffeners that are integrated as enhancements against external impacts. Considering von-Kármán geometric nonlinearity and smeared oblique stiffeners, the dynamic governing equation is derived by capitalizing on Airy’s stress function and the Galerkin approach. The deduced nonlinear motion equation can be effectively solved by the fourth-order Runge–Kutta method, such that the natural frequency, wind-induced nonlinear vibration behaviour, and dynamic buckling characteristics of the stiffened PSC can be assessed. The accuracy of the developed framework is verified with established benchmarks. Moreover, the effects of the damping ratio, thermal variance, wind load, compression speed, elastic foundation, initial imperfection, compression ratio, oblique stiffeners, and active layer thickness on the structural response and stability are thoroughly examined. Concluding remarks, drawn from this study, on the mechanical performance and stability of the novel PSC will benefit the practical design and application of PSC energy harvesting devices.

1 Introduction

The rapid growth of the population and economy has long been a global issue that intensifies the demand and consumption of the world’s energy resources [1]. This looming challenge has stimulated the spotlight research of unlimited and environmentally friendly solar energy, which is deemed a latent remedy to alleviate global climate change and the energy crisis for the sustainable development of human civilization [2, 3]. Currently, following the ambitious vision of carbon neutrality, various countries have responsibly established manifold incentives to catalyse the versatile applications of solar products [4, 5].

Under the encouraging strategic initiatives, new photovoltaic innovations stand out as key ingredients of the modern recipe for sustainability. Amidst them, the emergence of the perovskite solar cell (PSC) has launched a revolution within third-generation electro-optic products, due to its superior traits in economical manufacturing and high solar absorption rate [6, 7]. It expeditiously converts sunlight into electricity and furnishes fruitful insights into future solar energy harvesting devices. With the record power conversion efficiency (PCE) exceeding 25% [8], researchers and industries are fascinated in further studying and harnessing the optimal performance and potential applications beyond laboratory experiments (Fig. 1). Diverse state-of-the-art photovoltaic companies, such as Hunt Perovskite Technologies and the Microquanta Semiconductor, are enthusiastically dedicated to the development of PSC devices for commercial production. These joint efforts serve as the brush in sketching a liveable future with clean energy and a graceful environment.

Fig. 1

The potential applications of the PSC. a The PSC for astronautics [9]; b solar façade [10]; c solar portable device [11]

During the thriving voyage towards practical deployment of the novel PSC, the investigation of the dynamic mechanical performance and stability of the structure represents an urgent and essential issue. These attributes manifest an indivisible relation with the device operating capacity and have a significant impact on the product service life. For example, the vibration characteristic can be exploited to develop clean solar products and enhance efficiency [12, 13]. However, such a double-edged sword might also trigger structural damage and underlying degradation [14, 15]. Hence, meticulous exploration of the dynamic behaviour is essential for optimizing the working capacity of PSC products. In addition, considering the ultra-thin characteristics of the structure, the PSC is highly susceptible to buckling failure under dynamic impacts. Therefore, it is imperative to examine plate stability and strengthen the structural capability against external loadings, which is indispensable for guaranteeing the safety of devices [16]. Otherwise, hazardous buckling failure and the structural damage might occur. Moreover, given the promising application of the PSC as a solar façade, it may not only suffer from dynamic impacts, i.e. strong winds and earthquakes, but also undergo exposure to environmental effects, such as thermal variations. The PSC usually rests on soil or elastic foundations. Nevertheless, the dynamic performance as well as various environmental effects have not yet been well investigated [17]. During space navigation, solar panels are fully unfolded to provide power for satellites. Nonetheless, pervasive high-energy particles and cosmic debris travel at high velocity, corresponding to unavoidable fierce impacts on photovoltaic systems. In this case, the PSC might suddenly surpass its loading resistance limit and become unstable under multiple high-speed impacts. Therefore, the dynamic behaviour and the structure stability should be scrutinized to ensure the device’s continual operation under diverse intricate circumstances [18]. However, in the reported literature, few studies have been committed to the dynamic mechanical performance and stability of the PSC [19], whereas the existing research primarily revolves around its chemical composition and optimal efficiency [7, 20]. Such a research gap hampers the real-life implementation of the PSC, let alone mass production in the industry [21, 22].

In reported studies on the mechanical performance of organic solar cells and such laminated composites, Duc et al. [23] and Dat et al. [24] revealed the nonlinear vibration behaviour and stability of multi-layer organic solar cells with effects of geometry, thickness, and imperfection. Based on third-order shear deformation theory, Li et al. [25] implemented harmonic vibration analysis of composite beams and reported the critical influence of graphene nanoplatelets in decreasing the resonant response. Chen et al. [26] performed a bending and buckling analysis of a porous structure through the Chebyshev–Ritz method and discovered the significant influence of porosity on stress mismatch and on the improvement of buckling performance. Li et al. [27] and Gao et al. [28, 29] studied the nonlinear dynamic behaviour of composite beams and plates resting on elastic foundations with the effects of temperature and damping. Gupta and Talha [30, 31] explored the vibration response and post-buckling characteristics of functionally graded plates through the finite element method and variation approach. Santana et al. [32] presented the nonlinear dynamic analysis of a space truss with material nonlinearity and identified the influence of truss geometry on structure performance under compressive loadings.

Recently, by employing the perturbation approach, the post-buckling behaviours of laminated plates and sandwich structures with auxetic cores have been explored by Shen et al. [33] and Chen et al. [34]. Nešić et al. [35] revealed the nonlinear frequency-amplitude response of micro-beams on visco-Pasternak elastic foundations. Li et al. [36,37,38] presented the first study on the nonlinear bending and dynamic behaviour of a functionally graded auxetic composite through both numerical and experimental analyses. An innovative three-dimensional lattice metamaterial with a negative Poisson’s ratio was designed, and a decrease in structure deflection due to the auxetic core was discovered. Li et al. [39] discussed the nonlinear vibration behaviour of piezoelectric laminated shells under harmonic dynamic loads. Wang et al. [40, 41] investigated the nonlinear free vibration and post-buckling performance of a multi-layer composite under electrical loadings, based on the differential quadrature method. The static lateral-torsional buckling characteristics of reinforced arches were presented by Liu et al. [42], and the effect of graphene platelet reinforcements on structure capacity was revealed. Yang et al. [43] implemented the dynamic buckling analysis of shallow arches through both theoretical and experimental approaches. By leveraging the Ritz method, Coaquira et al. [44] conducted vibration analysis of fibre-reinforced polymer columns and reported that the composite might lose stability at loading intensities below static buckling loads under dynamic excitations. The complex dynamic characteristics of composite pipes for conveying fluid were observed by Reddy et al. [45]. Liu et al. [46] presented the nonlinear forced vibration of porous cylindrical shells and identified the influences of the core thickness and porosity volume fraction on the frequency–response relation. Zhu et al. [47] explored the free vibration behaviour of functionally graded plates with cracks and reflected the sensitivity of the composite frequency to cracks.

To lower the weight while strengthening the structure performance, stiffeners have been introduced as reinforcements. They enjoy widespread applications across civil and aerospace engineering, such as aircraft, nuclear reactors, and offshore platforms. In stiffened structure analysis, the smeared stiffener technique manifests a general and efficient computational approach, where the composite with stiffeners is transformed mathematically into the equivalent laminate with identical stiffness [48]. Based on this technique, Bich et al. [49] discussed the free vibration and dynamic behaviour of stiffened cylindrical panels. Duc et al. [50] and Quan et al. [51] examined the nonlinear dynamic stability and post-buckling characteristics of functionally graded panels and shells with oblique stiffener reinforcements. Foroutan et al. [52] performed a static and dynamic buckling analysis of stiffened cylindrical shells under axial compression. Ahmadi et al. [53] reported the vibration behaviour of a stiffened functionally graded shell resting on a nonlinear elastic foundation.

To the best of the authors’ knowledge, there is still a lack of systematic research on the dynamic behaviour and performance of the novel PSC, as well as feasible reinforcements on its structure capacity against external impacts. Such exploration is closely related to the PSC product’s operating capacity, stability and service time. In addition, analytical examination of the nonlinear dynamic buckling behaviour under biaxial impacts has been rare. Sporadic studies have incorporated comprehensive practical effects such as the damping ratio, thermal variance, wind load, impact speed, elastic foundation, initial imperfection, compression ratio, oblique stiffeners, and active layer thickness. Nonetheless, multiple speedy impacts and various practical effects universally exist in the deployment of PSC devices and have a significant influence on the mechanical attributes of structures.

With the aim of ameliorating the above problem and investigating the mechanical characteristics and stability of the newly developed PSC for further real-life implementations, the present study examines the structure nonlinear vibration behaviour and buckling response under biaxial impacts. Because of the ultra-thin characteristics of the composite, the PSC is highly vulnerable to buckling failure. Hence, oblique stiffeners have been integrated to intensify the structure stiffness against external excitations. A simulated wind load is exerted on the stiffened PSC for study, given the frequent cases of dynamic loadings on the solar façade. The biaxial impacts are imposed by velocity compressions in the longitudinal directions, resembling the solar automobile and space shuttle in high-speed industry. Employing the von-Kármán strain–displacement relation and smeared stiffener technique, the nonlinear dynamic response and buckling equation can be derived by Airy’s stress function and the Galerkin approach. Subsequently, the fourth-order Runge–Kutta method is implemented to obtain the solution in a robust manner. The results can be formulated explicitly in terms of various parameters in an efficient fashion. Therefore, it might be convenient to change these parameters during the design for response control of the stiffened PSC. In addition, to accommodate manifold practical effects and fulfil a more generalized determination framework, the effects of the damping ratio, thermal variance, wind load, impact speed, elastic foundation, initial imperfection, compression ratio, oblique stiffeners, and active layer thickness on the structural response are investigated through the numerical study. The present research contributes to the future deployment of the novel PSC with strengthened structural capability against external impacts and safety.

The remainder of this paper is arranged as follows. The fundamental theory and basic formulations for nonlinear dynamic analysis of the stiffened PSC are presented in Sect. 2. In Sect. 3, the Galerkin approach is utilized to obtain the dynamic buckling equation under biaxial impacts. Then, the fourth-order Runge–Kutta method is leveraged to solve the dynamic equation and capture the structure response. In Sect. 4, the verification of established benchmarks with existing research, and a parametric study of the PSC dynamic performance are reported. Eventually, some concluding remarks are recapitulated in Sect. 5.

2 Fundamental theory and formulation

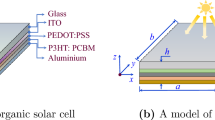
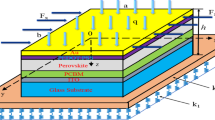
In this work, a simply supported PSC reinforced with oblique stiffeners at the bottom resting on the nonlinear elastic foundation is considered, as illustrated in Fig. 2. The geometries of the PSC are length $a$, width $b$, and thickness $h$. The parameters of the stiffeners are the spacing $s_{s}$, width $d_{s}$, thickness $h_{s}$, angle $\theta_{x}$, and angle $\theta_{y}$, as shown in Fig. 3. The structure of the PSC consists of 6 layers, comprising the Au layer, hole-transporting layer, perovskite layer, mesoporous layer, electron-transporting layer, and fluorine-doped tin oxide (FTO) layer [54]. The mesoporous layer is a mixture of perovskite with a volume fraction of 30% and TiO₂ with a volume fraction of 70%. The property of this layer can be obtained through the rule of mixture [55, 56]. The stiffened PSC is postulated as a whole laminate. Each layer is assumed to be strictly bonded with two adjacent layers. The Cartesian coordinate frame $(x,y,z)$ is built with the $(x,y)$ plane situated in the middle-surface and the z-axis denoting the thickness direction. The lth layer lies between $z = z_{l}$ and $z = z_{l + 1}$. Biaxial impacts with constant velocity compressions are exerted on the longitudinal edges, and a uniformly distributed wind load is applied on top of the plate.

Fig. 2

a The PSC with oblique stiffener reinforcements resting on the nonlinear elastic foundation. b The structure of the stiffened PSC

Fig. 3

Geometry of oblique stiffeners

Based upon Hooke’s law, the constitutive equation of the lth layer in the PSC under uniform thermal circumstances is presented as [57]

$$ \left[ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{xy} \hfill \\ \end{aligned} \right]_{l} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]_{l} \left[ \begin{aligned} \varepsilon_{xx} - \varepsilon_{xx}^{T} \\ \varepsilon_{yy} - \varepsilon_{yy}^{T} \\ \gamma_{xy} \\ \end{aligned} \right]_{l} $$

(1a)

and for stiffeners as

$$ \left[ \begin{aligned} \sigma_{xx}^{s} \hfill \\ \sigma_{yy}^{s} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {E_{s} } & 0 \\ 0 & {E_{s} } \\ \end{array} } \right]\left[ \begin{aligned} \varepsilon_{xx} \\ \varepsilon_{yy} \\ \end{aligned} \right] $$

(1b)

where $(C_{11} )_{l} = \frac{{E_{l} }}{{1 - \nu_{l}^{2} }},(C_{12} )_{l} = \frac{{\nu_{l} E_{l} }}{{1 - \nu_{l}^{2} }},(C_{22} )_{l} = \frac{{E_{l} }}{{1 - \nu_{l}^{2} }},(C_{66} )_{l} = \frac{{E_{l} }}{{2(1 + \nu_{l} )}}$; $E_{l}$ and $E_{s}$ are the Young’s modulus of the lth layer in the PSC and stiffeners, respectively. The thermal strains have the following forms:

$$ \left\{ \begin{aligned} \varepsilon_{xx}^{T} = \alpha_{x} \Delta T(x,y,z,t) \hfill \\ \varepsilon_{yy}^{T} = \alpha_{y} \Delta T(x,y,z,t) \hfill \\ \end{aligned} \right. $$

(2)

where $\alpha_{x}$ and $\alpha_{y}$ indicate the linear thermal expansion coefficients along the x- and y-axes, respectively. The thermal expansion coefficients along the x- and y-axes are assumed to be equal for each layer of the PSC. $\Delta T$ represents the increase in temperature from the ambient environment.

Grounded in Kirchhoff plate theory, the von-Kármán nonlinear strain–displacement relation is defined as [57]:

$$ \left[ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \gamma_{xy} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} \varepsilon_{xx}^{0} \hfill \\ \varepsilon_{yy}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ \end{aligned} \right] + z\left[ \begin{aligned} \varepsilon_{xx}^{1} \hfill \\ \varepsilon_{yy}^{1} \hfill \\ \gamma_{xy}^{1} \hfill \\ \end{aligned} \right] $$

(3)

where

$$ \left[ \begin{aligned} \varepsilon_{xx}^{0} \hfill \\ \varepsilon_{yy}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ \end{aligned} \right]{ = }\left[ \begin{aligned} \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} \hfill \\ \frac{\partial v}{{\partial y}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} \hfill \\ \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}} \hfill \\ \end{aligned} \right] $$

(4)

$$ \left[ \begin{aligned} \varepsilon_{xx}^{1} \hfill \\ \varepsilon_{yy}^{1} \hfill \\ \gamma_{xy}^{1} \hfill \\ \end{aligned} \right]{ = }\left[ \begin{aligned} - \frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ - \frac{{\partial^{2} w}}{{\partial y^{2} }} \hfill \\ - 2\frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \end{aligned} \right] $$

(5)

in which $u$, $v$, and $w$, respectively, denote the components of displacement in the $x,y,z$ directions.

Given the effect of smeared oblique stiffeners, the force and moment resultants of the stiffened PSC are expressed as

$$ \left[ \begin{aligned} N_{xx} \hfill \\ N_{yy} \hfill \\ N_{xy} \hfill \\ M_{xx} \hfill \\ M_{yy} \hfill \\ M_{xy} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {I_{11} } & {I_{12} } & {I_{16} } & {J_{11} } & {J_{12} } & {J_{16} } \\ {I_{12} } & {I_{22} } & {I_{26} } & {J_{12} } & {J_{22} } & {J_{26} } \\ {I_{16} } & {I_{26} } & {I_{66} } & {J_{16} } & {J_{26} } & {J_{66} } \\ {J_{11} } & {J_{12} } & {J_{16} } & {K_{11} } & {K_{12} } & {K_{16} } \\ {J_{12} } & {J_{22} } & {J_{26} } & {K_{12} } & {K_{22} } & {K_{26} } \\ {J_{16} } & {J_{26} } & {J_{66} } & {K_{16} } & {K_{26} } & {K_{66} } \\ \end{array} } \right]\left[ \begin{aligned} \varepsilon_{xx}^{0} \\ \varepsilon_{yy}^{0} \\ \gamma_{xy}^{0} \\ \varepsilon_{xx}^{1} \\ \varepsilon_{yy}^{1} \\ \gamma_{xy}^{1} \\ \end{aligned} \right] - \left[ \begin{aligned} (\overline{{I_{11} }} + \overline{{I_{12} }} )\varepsilon_{xx}^{T} \hfill \\ (\overline{{I_{12} }} + \overline{{I_{22} }} )\varepsilon_{xx}^{T} \hfill \\ 0 \hfill \\ (\overline{{J_{11} }} + \overline{{J_{12} }} )\varepsilon_{xx}^{T} \hfill \\ (\overline{{J_{12} }} + \overline{{J_{22} }} )\varepsilon_{xx}^{T} \hfill \\ 0 \hfill \\ \end{aligned} \right] $$

(6)

where the detailed coefficients $I_{ij} , \, J_{ij} , \, K_{ij} , \, \overline{{I_{ij} }} , \, \overline{{J_{ij} }} , \, \overline{{K_{ij} }}$ are defined in the Appendix.

To accommodate damping effects, the nonlinear dynamic equilibrium equations of the stiffened PSC resting on the nonlinear elastic foundation under uniform thermal variation and out-of-plane wind load $q$ are formulated as

$$ \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \rho h\frac{{\partial^{2} u}}{{\partial t^{2} }} + C_{d} \rho h\frac{\partial u}{{\partial t}} $$

(7)

$$ \frac{{\partial N_{yy} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} = C_{d} \rho h\frac{\partial v}{{\partial t}} + \rho h\frac{{\partial^{2} v}}{{\partial t^{2} }} $$

(8)

$$ \begin{aligned} & N_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} \\ \quad + k_{p} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + q - k_{w} w - k_{n} w^{3} = C_{d} \rho h\frac{\partial w}{{\partial t}} + \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned} $$

(9)

where $C_{d}$ is the damping coefficient; $k_{p}$ denotes the Pasternak shear layer stiffness; $k_{w}$ indicates the Winkler foundation coefficient; and $k_{n}$ represents the nonlinear cubic stiffness. Assuming that the flexural deflection is determinant in the deformation of the whole structure [58], $\frac{{\partial^{2} u}}{{\partial t^{2} }}$, $\frac{{\partial^{2} v}}{{\partial t^{2} }}$, $\frac{\partial u}{{\partial t}}$, and $\frac{\partial v}{{\partial t}}$ can be neglected.

By incorporating the initial imperfection $w_{0} (x,y)$, the geometric compatibility relation can be determined as

$$ \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{0} }}{\partial x\partial y} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} $$

(10)

Then, Airy’s stress function is introduced as

$$ N_{xx} = \frac{{\partial^{2} f}}{{\partial y^{2} }},\quad N_{yy} = \frac{{\partial^{2} f}}{{\partial x^{2} }},\quad N_{xy} = - \frac{{\partial^{2} f}}{\partial x\partial y} $$

(11)

From Eq. (6), the membrane strains and moment resultants of the stiffened PSC can be calculated as

$$ \left[ \begin{aligned} \varepsilon_{xx}^{0} \hfill \\ \varepsilon_{yy}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ \end{aligned} \right]{ = }\left[ \begin{aligned} I_{11}^{*} N_{xx} + I_{12}^{*} N_{yy} + I_{16}^{*} N_{xy} + J_{11}^{*} \varepsilon_{xx}^{1} + J_{12}^{*} \varepsilon_{yy}^{1} + J_{16}^{*} \gamma_{xy}^{1} + I_{17}^{*} \varepsilon_{xx}^{T} \\ I_{21}^{*} N_{xx} + I_{22}^{*} N_{yy} + I_{26}^{*} N_{xy} + J_{21}^{*} \varepsilon_{xx}^{1} + J_{22}^{*} \varepsilon_{yy}^{1} + J_{26}^{*} \gamma_{xy}^{1} + I_{27}^{*} \varepsilon_{xx}^{T} \\ I_{61}^{*} N_{xx} + I_{62}^{*} N_{yy} + I_{66}^{*} N_{xy} + J_{61}^{*} \varepsilon_{xx}^{1} + J_{62}^{*} \varepsilon_{yy}^{1} + J_{66}^{*} \gamma_{xy}^{1} + I_{67}^{*} \varepsilon_{xx}^{T} \\ \end{aligned} \right] $$

(12)

$$ \left[ \begin{aligned} M_{xx}^{{}} \hfill \\ M_{yy}^{{}} \hfill \\ M_{xy}^{{}} \hfill \\ \end{aligned} \right]{ = }\left[ \begin{aligned} \overline{{I_{11}^{*} }} N_{xx} + \overline{{I_{12}^{*} }} N_{yy} + \overline{{I_{16}^{*} }} N_{xy} + \overline{{J_{11}^{*} }} \varepsilon_{xx}^{1} + \overline{{J_{12}^{*} }} \varepsilon_{yy}^{1} + \overline{{J_{16}^{*} }} \gamma_{xy}^{1} + \overline{{I_{17}^{*} }} \varepsilon_{xx}^{T} \\ \overline{{I_{21}^{*} }} N_{xx} + \overline{{I_{22}^{*} }} N_{yy} + \overline{{I_{26}^{*} }} N_{xy} + \overline{{J_{21}^{*} }} \varepsilon_{xx}^{1} + \overline{{J_{22}^{*} }} \varepsilon_{yy}^{1} + \overline{{J_{26}^{*} }} \gamma_{xy}^{1} + \overline{{I_{27}^{*} }} \varepsilon_{xx}^{T} \\ \overline{{I_{61}^{*} }} N_{xx} + \overline{{I_{62}^{*} }} N_{yy} + \overline{{I_{66}^{*} }} N_{xy} + \overline{{J_{61}^{*} }} \varepsilon_{xx}^{1} + \overline{{J_{62}^{*} }} \varepsilon_{yy}^{1} + \overline{{J_{66}^{*} }} \gamma_{xy}^{1} + \overline{{I_{67}^{*} }} \varepsilon_{xx}^{T} \\ \end{aligned} \right] $$

(13)

where the detailed coefficients $I_{ij}^{*} , \, J_{ij}^{*} , \, \overline{{I_{ij}^{*} }} , \, \overline{{J_{ij}^{*} }}$ can be found in the Appendix.

By substituting Eq. (12) into Eq. (10), the nonlinear compatibility relation can be rewritten as

$$ \begin{aligned} & (I_{21}^{*} + I_{12}^{*} + I_{66}^{*} )\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + I_{22}^{*} \frac{{\partial^{4} f}}{{\partial x^{4} }} - (I_{26}^{*} + I_{62}^{*} )\frac{{\partial^{4} f}}{{\partial x^{3} \partial y}} - \frac{{\partial^{4} w}}{{\partial x^{4} }}J_{21}^{*} - (2J_{26}^{*} - J_{61}^{*} )\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} \\ &\qquad + I_{11}^{*} \frac{{\partial^{4} f}}{{\partial y^{4} }} - \frac{{\partial^{4} f}}{{\partial x\partial y^{3} }}(I_{16}^{*} + I_{61}^{*} ) - \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}(J_{11}^{*} + J_{22}^{*} - 2J_{66}^{*} ) - \frac{{\partial^{4} w}}{{\partial y^{4} }}J_{12}^{*} - \frac{{\partial^{4} w}}{{\partial x\partial y^{3} }}(2J_{16}^{*} - J_{62}^{*} ) \\ &\quad = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} \\ \end{aligned} $$

(14)

Substituting Eqs. (11) and (13) into Eq. (9), the nonlinear equilibrium equation of motion can be reformulated as

$$ \begin{aligned} & S_{3} \frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + S_{1} \frac{{\partial^{4} f}}{{\partial x^{4} }} + S_{2} \frac{{\partial^{4} f}}{{\partial y^{4} }} + S_{4} \frac{{\partial^{4} f}}{{\partial x^{3} \partial y}} + S_{5} \frac{{\partial^{4} f}}{{\partial x\partial y^{3} }} + S_{6} \frac{{\partial^{4} w}}{{\partial x^{4} }} + S_{7} \frac{{\partial^{4} w}}{{\partial y^{4} }} \\ &\quad + S_{8} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + S_{9} \frac{{\partial^{3} w}}{{\partial x^{3} \partial y}} + S_{10} \frac{{\partial^{4} w}}{{\partial x\partial y^{3} }} + \frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\left( { - \frac{{\partial^{2} f}}{\partial x\partial y}} \right)\frac{{\partial^{2} w}}{\partial x\partial y} \\ &\quad + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + k_{p} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + q - k_{w} w - k_{n} w^{3} = C_{d} \rho h\frac{\partial w}{{\partial t}} + \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned} $$

(15)

where

$$ \begin{aligned} &S_{1} = \overline{{I_{12}^{*} }} ,\quad S_{2} = \overline{{I_{21}^{*} }} ,\quad S_{3} = (\overline{{I_{11}^{*} }} + \overline{{I_{22}^{*} }} - 2\overline{{I_{66}^{*} }} ),\quad \hfill \\ &S_{4} = - \overline{{I_{16}^{*} }} + 2\overline{{I_{62}^{*} }} ,\quad S_{5} = 2\overline{{I_{61}^{*} }} - \overline{{I_{26}^{*} }} , \hfill \\ &S_{6} = - \overline{{J_{11}^{*} }} ,\quad S_{7} = - \overline{{J_{22}^{*} }} ,\quad S_{8} = - \overline{{J_{12}^{*} }} - \overline{{J_{21}^{*} }} - 4\overline{{J_{66}^{*} }} , \, \hfill \\ &S_{9} = - 2\overline{{J_{16}^{*} }} - 2\overline{{J_{61}^{*} }} ,\quad S_{10} = - 2\overline{{J_{26}^{*} }} - 2\overline{{J_{62}^{*} }} \hfill \\ \end{aligned} $$

(16)

For the initial imperfect stiffened PSC, the governing equation of motion can be deduced as

$$ \begin{aligned} & S_{3} \frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + S_{1} \frac{{\partial^{4} f}}{{\partial x^{4} }} + S_{2} \frac{{\partial^{4} f}}{{\partial y^{4} }} + S_{4} \frac{{\partial^{4} f}}{{\partial x^{3} \partial y}} + S_{5} \frac{{\partial^{4} f}}{{\partial x\partial y^{3} }} + S_{6} \frac{{\partial^{4} w}}{{\partial x^{4} }} + S_{7} \frac{{\partial^{4} w}}{{\partial y^{4} }} + S_{8} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} \\ &\quad + S_{9} \frac{{\partial^{3} w}}{{\partial x^{3} \partial y}} + S_{10} \frac{{\partial^{4} w}}{{\partial x\partial y^{3} }} + \frac{{\partial^{2} f}}{{\partial y^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right){ + }2\left( { - \frac{{\partial^{2} f}}{\partial x\partial y}} \right)\left( {\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right) \\ &\quad + \frac{{\partial^{2} f}}{{\partial x^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) + k_{p} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + q - k_{w} w - k_{n} w^{3} = C_{d} \rho h\frac{\partial w}{{\partial t}} + \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned} $$

(17)

3 Nonlinear dynamic analysis of the stiffened PSC

Two cases of boundary conditions are included in this section. The first is that four edges of the stiffened PSC are assumed to be simply supported and movable:

$$ \begin{aligned} \left. \begin{aligned} w = M_{yy} = N_{xy} = 0 \hfill \\ N_{yy} = N_{y}^{0} \hfill \\ \end{aligned} \right\}y = 0,b \hfill \\ \left. \begin{aligned} w = M_{xx} = N_{xy} = 0 \hfill \\ N_{xx} = N_{x}^{0} \hfill \\ \end{aligned} \right\}x = 0,a \hfill \\ \end{aligned} $$

(18)

in which $N_{x}^{0} = - p_{x} (t)h$ and $N_{y}^{0} = - p_{y} (t)h$, respectively, indicate the virtual compressions in the x-axis and y-axis.

The second is that four edges are simply supported and immovable:

$$ \begin{aligned} \left. \begin{aligned} w = v = M_{yy} = N_{xy} = 0 \hfill \\ N_{yy} = N_{y}^{0} \hfill \\ \end{aligned} \right\}y = 0,b \hfill \\ \left. \begin{aligned} w = u = M_{xx} = N_{xy} = 0 \hfill \\ N_{xx} = N_{x}^{0} \hfill \\ \end{aligned} \right\}x = 0,a \hfill \\ \end{aligned} $$

(19)

To satisfy the above boundary conditions, the solution of deflection $w$ is assumed to be [59]

$$ w(x,y,t) = W(t)\sin \left( {\frac{\pi mx}{a}} \right)\sin \left( {\frac{\pi ny}{b}} \right) $$

(20)

where $W(t)$ is the time-varying amplitude of deflection; $m$ and $n$ denote the number of half-waves along the x- and y-axes, respectively. In addition, other boundary conditions can be incorporated by utilizing the appropriate admissible function [60].

Similarly, the initial imperfection shape function is given as

$$ w_{0} (x,y,t) = W_{0} \sin \left( {\frac{\pi mx}{a}} \right)\sin \left( {\frac{\pi ny}{b}} \right) $$

(21)

in which $W_{0}$ represents the initial imperfection amplitude of the stiffened PSC.

By substituting Eqs. (20) and (21) into compatibility relation Eq. (14), the stress function that satisfies the boundary conditions can be deduced as

$$ \begin{aligned} f(x,y,t) & = F_{1} W(W + 2W_{0} )\cos (2\alpha x) + F_{2} W(W + 2W_{0} )\cos (2\beta y) \\ &\quad + F_{3} W\sin (\alpha x)\sin (\beta y) + F_{4} W\cos (\alpha x)\cos (\beta y) + \frac{1}{2}N_{x}^{0} y^{2} + \frac{1}{2}N_{y}^{0} x^{2} \\ \end{aligned} $$

(22)

where

$$ \begin{aligned} F_{31} = (I_{21}^{*} + I_{12}^{*} + I_{66}^{*} )\alpha^{2} \beta^{2} + I_{22}^{*} \alpha^{4} + I_{11}^{*} \beta^{4} , \hfill \\ F_{32} = (I_{26}^{*} + I_{62}^{*} )\beta \alpha^{3} + (I_{16}^{*} + I_{61}^{*} )\beta^{3} \alpha ,\quad \alpha = \frac{\pi m}{a}, \, \hfill \\ F_{33} = J_{21}^{*} \alpha^{4} + (J_{11}^{*} + J_{22}^{*} - 2J_{66}^{*} )\alpha^{2} \beta^{2} + J_{12}^{*} \beta^{4} , \hfill \\ F_{34} = ( - 2J_{26}^{*} + J_{61}^{*} )\alpha^{3} \beta + ( - 2J_{16}^{*} + J_{62}^{*} )\alpha \beta^{3} , \, \hfill \\ \beta = \frac{\pi n}{b},\quad F_{1} = \frac{{\beta^{2} }}{{32I_{22}^{*} \alpha^{2} }},\quad F_{2} = \frac{{\alpha^{2} }}{{32I_{11}^{*} \beta^{2} }}, \hfill \\ F_{3} = \frac{{F_{31} F_{33} - F_{32} F_{34} }}{{F_{31}^{2} - F_{32}^{2} }},\quad F_{4} = \frac{{ - F_{32} F_{33} + F_{31} F_{34} }}{{F_{31}^{2} - F_{32}^{2} }} \hfill \\ \end{aligned} $$

(23)

By substituting Eqs. (20)–(23) into Eq. (17) and capitalizing on the Galerkin approach, the governing equation of motion can be represented as

$$ \begin{aligned} & G_{1} (W + 2W_{0} )W + G_{2} W + G_{4} (W + W_{0} )(W + 2W_{0} )W \\ \quad + G_{5} (W + W_{0} )W + G_{6} q - (N_{x}^{0} \alpha^{2} + N_{y}^{0} \beta^{2} )(W + W_{0} ) \\ \quad - [k_{p} (\alpha^{2} + \beta^{2} ) + k_{w} ]W - \frac{9}{16}k_{n} W^{3} \\ = C_{d} \rho h\frac{\partial W}{{\partial t}} + \rho h\frac{{\partial^{2} W}}{{\partial t^{2} }} \\ \end{aligned} $$

(24)

in which

$$ \begin{aligned} &G_{1} = - \frac{256}{{3\beta ab}}S_{1} \alpha^{3} F_{1} - \frac{256}{{3\alpha ab}}S_{2} \beta^{3} F_{2} \hfill \\ &G_{2} = S_{3} F_{3} \alpha^{2} \beta^{2} + S_{1} \alpha^{4} F_{3} + S_{2} \beta^{4} F_{3} - S_{4} F_{4} \alpha^{3} \beta \hfill \\ &- S_{5} F_{4} \alpha \beta^{3} + S_{6} \alpha^{4} + S_{7} \beta^{4} + S_{8} \alpha^{2} \beta^{2} \hfill \\ &G_{4} = - 2\alpha^{2} \beta^{2} F_{2} - 2\alpha^{2} \beta^{2} F_{1} \hfill \\ G_{5} = F_{3} \frac{32\alpha \beta }{{3ab}} \hfill \\ &G_{6} = \frac{16}{{\alpha \beta ab}} \hfill \\ \end{aligned} $$

(25)

From Eqs. (4) and (12), taking the initial eccentricity into account, $\partial u/\partial x$ and $\partial v/\partial y$ subsequently become

$$ \begin{aligned}\frac{\partial u}{{\partial x}} &= I_{11}^{*} N_{xx} + I_{12}^{*} N_{yy} + I_{16}^{*} N_{xy} + J_{11}^{*} \varepsilon_{xx}^{1} + J_{12}^{*} \varepsilon_{yy}^{1} + J_{16}^{*} \gamma_{xy}^{1} \\ &\quad + I_{17}^{*} \varepsilon_{xx}^{T} - \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - \frac{\partial w}{{\partial x}}\frac{{\partial w_{0} }}{\partial x} \end{aligned}$$

(26a)

$$ \begin{aligned}\frac{\partial v}{{\partial y}}& = I_{21}^{*} N_{xx} + I_{22}^{*} N_{yy} + I_{26}^{*} N_{xy} + J_{21}^{*} \varepsilon_{xx}^{1} + J_{22}^{*} \varepsilon_{yy}^{1}\\ & + J_{26}^{*} \gamma_{xy}^{1} + I_{27}^{*} \varepsilon_{xx}^{T} - \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} - \frac{\partial w}{{\partial y}}\frac{{\partial w_{0} }}{\partial y}\end{aligned} $$

(26b)

The stiffened PSC is subjected to dynamic biaxial impacts along the x- and y-axes with velocity compressions. The relative displacements in the x and y directions are presented as

$$ U_{x} = \int_{0}^{a} {\int_{0}^{b} {\frac{\partial u}{{\partial x}}} } \;{\text{d}}y{\text{d}}x = - vt $$

(27a)

$$ U_{y} = \int_{0}^{a} {\int_{0}^{b} {\frac{\partial v}{{\partial y}}} } \;{\text{d}}y{\text{d}}x = - \alpha_{v} vt $$

(27b)

where $\alpha_{v}$ indicates the axial compression ratio.

From Eqs. (26a) to (27b), the value of the average compression force can be computed as

$$ N_{x}^{0} { = }\lambda_{11} vt + \lambda_{12} W + \lambda_{13} W^{2} + \lambda_{14} WW_{0} + \lambda_{15} \varepsilon_{xx}^{T} $$

(28a)

$$ N_{y}^{0} { = }\lambda_{21} vt + \lambda_{22} W + \lambda_{23} W^{2} + \lambda_{24} WW_{0} + \lambda_{25} \varepsilon_{xx}^{T} $$

(28b)

$$ p_{x} (t){ = } - {{N_{x}^{0} } \mathord{\left/ {\vphantom {{N_{x}^{0} } h}} \right. \kern-\nulldelimiterspace} h} $$

(28c)

$$ p_{y} (t){ = } - {{N_{y}^{0} } \mathord{\left/ {\vphantom {{N_{y}^{0} } h}} \right. \kern-\nulldelimiterspace} h} $$

(28d)

where the coefficients $\lambda_{ij}$ are denoted in the Appendix.

3.1 Nonlinear vibration analysis

For linear free vibration, the fundamental natural frequency of the perfect stiffened PSC can be deduced as

$$ \omega_{mn}^{{}} { = }\sqrt { - \frac{{G_{2} - [k_{p} (\alpha^{2} + \beta^{2} ) + k_{w} ]}}{\rho h} - \frac{{(\alpha^{2} + \beta^{2} )p_{re} }}{\rho }} $$

(29)

where $p_{re} = p_{x} = p_{y}$ denote the pre-existing axial compressions.

The simulated wind pressure $q = \frac{1}{2}\gamma_{d} \rho_{w} V_{w}^{2} \sin \theta_{w} \, ({\text{Pa}})$ is presented in [61] and introduced herein, as demonstrated in Fig. 4, where $\gamma_{d}$ is the pressure coefficient; $\rho_{w}$ is the wind density equal to $1.235\;{\text{kg/m}}^{3}$; $V_{w}$ is the average wind speed; and $\theta_{w}$ is the wind angle determined by the directions of the wind and PSC surface. The wind pressure is postulated to be uniformly distributed on top of the stiffened PSC. Neglecting the compressive velocity, Eq. (24) can be further expressed as

$$ \begin{aligned} & G_{1} (W + 2W_{0} )W + G_{2} W + G_{4} (W + W_{0} )(W + 2W_{0} )W \\& \quad + G_{5} (W + W_{0} )W + G_{6} q - (\lambda_{12} W + \lambda_{13} W^{2} + \lambda_{14} WW_{0} + \lambda_{15} \varepsilon_{xx}^{T} )\alpha^{2} (W + W_{0} ) \\ &\quad - (\lambda_{22} W + \lambda_{23} W^{2} + \lambda_{24} WW_{0} + \lambda_{25} \varepsilon_{xx}^{T} )\beta^{2} (W + W_{0} ) - [k_{p} (\alpha^{2} + \beta^{2} ) + k_{w} ]W \\ & \quad - \frac{9}{16}k_{n} W^{3} = C_{d} \rho h\frac{\partial W}{{\partial t}} + \rho h\frac{{\partial^{2} W}}{{\partial t^{2} }} \\ \end{aligned} $$

(30)

where

$$ C_{d} = 2\omega_{mn}^{{}} \zeta $$

(31)

in which $\zeta$ denotes the damping ratio. Equation (30) is the wind-induced nonlinear vibration equation of the stiffened PSC.

Fig. 4

Impact of wind load on the stiffened PSC

3.2 Nonlinear dynamic biaxial buckling analysis

For the initial perfectly stiffened PSC, the static buckling behaviour can be calculated by ignoring the out-of-plane excitation, velocity, inertia, and high-order terms in Eq. (24).

$$ G_{2} - N_{x}^{0} \alpha^{2} - N_{y}^{0} \beta^{2} - [k_{p} (\alpha^{2} + \beta^{2} ) + k_{w} ] = 0 $$

(32)

The static critical buckling load can be determined regarding the smallest value as

$$ N_{st} = N_{y}^{0} = N_{x}^{0} = \frac{{[ - k_{p} (\alpha^{2} + \beta^{2} ) - k_{w} + G_{2} ]}}{{\alpha^{2} + \beta^{2} }} $$

(33)

$$ p_{st} { = }{{ - N_{st} } \mathord{\left/ {\vphantom {{ - N_{st} } h}} \right. \kern-\nulldelimiterspace} h} $$

(34)

The nonlinear dynamic biaxial buckling equation of the stiffened PSC can be derived by substituting the average compressive force Eqs. (28a)–(28d) into Eq. (24) as

$$ \begin{aligned} &G_{1} (W + 2W_{0} )W + G_{2} W + G_{4} (W + W_{0} )(W + 2W_{0} )W \hfill \\ &\quad + G_{5} (W + W_{0} )W - (\lambda_{11} vt + \lambda_{12} W + \lambda_{13} W^{2} + \lambda_{14} WW_{0} + \lambda_{15} \varepsilon_{xx}^{T} )\alpha^{2} (W + W_{0} ) \hfill \\ &\quad - (\lambda_{21} vt + \lambda_{22} W + \lambda_{23} W^{2} + \lambda_{24} WW_{0} + \lambda_{25} \varepsilon_{xx}^{T} )\beta^{2} (W + W_{0} ) \hfill \\ &\quad - [k_{p} (\alpha^{2} + \beta^{2} ) + k_{w} ]W - \frac{9}{16}k_{n} W^{3} = C_{d} \rho h\frac{\partial W}{{\partial t}} + \rho h\frac{{\partial^{2} W}}{{\partial t^{2} }} \hfill \\ \end{aligned} $$

(35)

Equation (35) can be solved by the fourth-order Runge–Kutta method and the dynamic buckling load can be computed with respect to Eqs. (28a)–(28d).

To intuitively illustrate the present investigation framework, a summarized flowchart for the nonlinear dynamic analysis of the stiffened PSC is presented in Fig. 5.

Fig. 5

Flowchart of the nonlinear dynamic analysis of the stiffened PSC

4 Numerical study

The properties of the stiffened PSC are summarized in Table 1. Other parameters of the plate are $a = b = 3.064 \times 10^{ - 3} {\text{ m}}$ [20], $h = 1429 \times 10^{ - 9} {\text{m}}$, $s_{s} = \frac{a}{20}$, $d_{s} = \frac{a}{50}$, $h_{s} = 2000\;{\text{nm}}$, $\theta_{x} = \frac{\pi }{6}$, $\theta_{y} = 0$, unless otherwise indicated. The ambient environmental temperature is adopted as $T = 300\;{\text{K}}$. Regarding the movable boundary conditions, the thermal coefficient is negative for increasing temperature, since the plate will lengthen and engender tension stress. For the immovable boundary conditions, the thermal coefficient is positive with regard to temperature rise. The immovable boundary conditions hinder the expansion of the stiffened PSC and result in the opposite compressive reaction within the plate. The verification and numerical study in this paper are implemented by employing MATLAB R2019b on an Intel(R) Core(TM) i7 CPU @2.90 GHz computer.

Table 1 Mechanical properties of different layers in the stiffened PSC [19, 21, 23, 54, 62,63,64,65]

4.1 Verification and parametric study of linear analysis

As there is no existing source of literature spotted in investigations of the PSC considering the current effects, the presented research is first validated with results from the finite element method software, ABAQUS. By ignoring the parameters of elastic foundations, various natural frequencies with respect to different modes are demonstrated in Table 2. The PSC plate with 10,000 meshed elements is modelled in ABAQUS for the sake of verification. From Table 2, the present research identifies with the commercial software. Hence, the reliability of the proposed study in terms of different modes is ensured.

Table 2 Natural frequencies of the PSC without the elastic foundation

In addition, the natural frequencies of the (Al/0_C)_S and (Al/0_G)_S laminated plates are investigated and compared with the recent research in Table 3. The geometry of the plate indicates $a = b = 0.25\;{\text{m}}$, $a/h = 80$. The properties of the aluminium denote $E_{{{\text{Al}}}} = 72\;{\text{GPa}}$, $G_{{{\text{Al}}}} = 28\;{\text{GPa}}$, $\rho_{{{\text{Al}}}} = 2700\;{\text{kg/m}}^{3}$, and $\nu_{{{\text{Al}}}} = 0.33$ [66]. The properties of the glass fibre-reinforced polymers (GFRP) are $E_{{{\text{GFRP}}1}} = 38.6\;{\text{GPa}}$, $E_{{{\text{GFRP}}2}} = 8.27{\text{ GPa}}$, $G_{{{\text{GFRP}}12}} = 4.14{\text{ GPa}}$, $\rho_{{{\text{GFRP}}}} = 1800\;{\text{kg/m}}^{3}$, and $\nu_{{{\text{GFRP}}12}} = 0.26$. The properties of the carbon fibre-reinforced polymers (CFRP) are $E_{{{\text{CFRP}}1}} = 181\;{\text{GPa}}$, $E_{{{\text{CFRP}}2}} = 10.3\;{\text{GPa}}$, $G_{{{\text{CFRP}}12}} = 7.17\;{\text{GPa}}$, $\rho_{{{\text{CFRP}}}} = 1600\;{\text{kg/m}}^{3}$, and $\nu_{{{\text{CFRP}}12}} = 0.28$. Al is the aluminium layer. Here, 0_C indicates the carbon fibre-reinforced polymer layer, and 0_G represents the glass fibre-reinforced polymer layer. From Table 3, the present method agrees with the existing benchmarks, which verifies the proposed dynamic analysis for multi-layer laminate composites.

Table 3 Natural frequencies of the laminated plates

The comparisons of dimensionless natural frequencies and static buckling loads of the orthotropic plate on elastic foundations are reported in Tables 4 and 5. The dimensions and properties of the plates are $a = b = 1.2\;{\text{m}}$, $h = 0.02a$, $E_{1} = 185\;{\text{GPa}}$, $E_{2} = 10.5\;{\text{GPa}}$, $G_{12} = 7.3\;{\text{GPa}}$, $\nu_{12} = 0.28$, $\nu_{21} = 0.01589$, and $\rho = 1600\;{\text{kg/m}}^{3}$. The dimensionless natural frequency, Winkler foundation coefficient, Pasternak stiffness, and static buckling load are defined as

$$ \begin{aligned} \widehat{{\omega_{mn} }} = \sqrt[4]{{\frac{{12\rho h\omega_{mn}^{2} (1 - \nu_{12} \nu_{21} )}}{{E_{1} h^{3} }}}}a,\quad \, \widehat{{K_{w} }} = \frac{{12k_{w} a^{4} (1 - \nu_{12} \nu_{21} )}}{{E_{1} h^{3} }}, \, \hfill \\ \widehat{{K_{p} }} = \frac{{12k_{p} a^{2} (1 - \nu_{12} \nu_{21} )}}{{E_{1} h^{3} }},\quad \, \widehat{{p_{st} }} = p_{st} \frac{{12a^{2} (1 - \nu_{12} \nu_{21} )}}{{E_{1} h^{2} \pi^{2} }} \hfill \\ \end{aligned} $$

(36)

Table 4 Dimensionless natural frequencies of the orthotropic plate with elastic foundations

Table 5 Dimensionless static buckling loads of the orthotropic plate with elastic foundations

From Tables 4 and 5, the dimensionless natural frequencies and static buckling loads in this paper are consistent with the literature, which illustrates the accuracy of the proposed research with elastic foundations.

Table 6 Nonlinear critical buckling loads ($\times$10⁸ Pa) of stiffened functionally graded plates

Similarly, since no literature can be found on the bucking behaviour of the stiffened PSC, the results of static and nonlinear dynamic buckling loads of stiffener-reinforced functionally graded laminated plates are provided in Table 6. The material properties are given as

$$ \begin{aligned} E(z) = E_{m} + (E_{c} - E_{m} )\left( {\frac{2z + h}{{2h}}} \right)^{k} \hfill \\ \rho (z) = \rho_{m} + (\rho_{c} - \rho_{m} )\left( {\frac{2z + h}{{2h}}} \right)^{k} \hfill \\ \end{aligned} $$

(37)

where $\nu = 0.3$, $a = b = 1.5\;{\text{m}}$, $E_{m} = 7 \times 10^{10} {\text{Pa}},$ $\rho_{m} = 2702\;{\text{kg/m}}^{3},$ $E_{c} = 380 \times 10^{9} {\text{Pa}},$ $\rho_{c} = 3800{\text{ kg/m}}^{3}$, $h = 0.008\;{\text{m}}$, $s_{s} = 0.15\;{\text{m}}$, $d_{s} = 3\;{\text{mm}}$, and $h_{s} = 30\;{\text{mm}}$. In [49], the stiffened laminated plate is subjected to an axial linearly increasing dynamic force $p(t) = c_{m} \times t$ with a loading rate $c_{m} = 1.5 \times 10^{9} {\text{ Pa/s}}$. The Budiansky–Roth criterion [68] is implemented to obtain the dynamic buckling load. From Table 6, a strong agreement is found between the present study and existing research, which verifies the proposed static and nonlinear dynamic analysis with stiffener reinforcements.

The influence of the Winkler–Pasternak elastic foundation on the natural frequency of the stiffened PSC is depicted in Fig. 6a. The increase in the Winkler–Pasternak elastic foundation parameters improves the natural frequency. In addition, a more significant impact of the Pasternak foundation stiffness, $k_{p}$, appears compared with the case of the Winkler foundation coefficient, $k_{w}$. Figure 6b shows the effects of pre-existing compressive loads and stiffeners. In addition to aluminium (Al), 4 other kinds of stiffener materials are selected for the purpose of comparison, as demonstrated in Table 7. The increase in axial compression yields a decrease in the natural frequency. In contrast with the unreinforced PSC, the natural frequency of stiffened plates exhibits a prominent increase. The maximum $\omega_{mn}^{{{\text{Nickel}}}} = 1071.0\;{\text{Hz}}$ is witnessed with the stiffener material of nickel, rising by 103.73 and 1.06% compared with the case of the unreinforced PSC and Al-stiffened structures. The natural frequencies of the magnesium-, glass-, and copper-stiffened PSC are $\omega_{mn}^{{{\text{Copper}}}} (940.0\;{\text{Hz}}) < \omega_{mn}^{{{\text{Magnesium}}}} (980.6\;{\text{Hz}}) < \omega_{mn}^{{{\text{Glass}}}} (1069.2\;{\text{Hz}})$.

Fig. 6

Natural frequencies (1, 1) of the stiffened PSC

Table 7 Properties of different materials [23, 69]

Figure 7a elucidates the impact of elastic foundation parameters on static buckling loads. The elastic foundation enhances the load carrying capacity and stability of the stiffened PSC. In addition, the Pasternak foundation plays a more important role in moderating buckling behaviour, which can be employed to preclude buckling failure. Figure 7b–f reflects the influences of the stiffener reinforcements and oblique angles. The oblique stiffeners possess favourable potential in decreasing buckling behaviour and enhancing structure stability. The peak buckling load $(p_{st} = 555,200\;{\text{Pa}})$ is observed at the stiffener angle of $(\theta_{x} ,\theta_{y} ) = \left( { - \frac{\pi }{4},\frac{\pi }{4}} \right)$ and the nickel material, which has the highest elastic modulus within the selection. The PSC with stiffeners that lie parallel to the edge of plates $(\theta_{x} ,\theta_{y} ) = \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right), \, \left( {\frac{\pi }{2},\frac{\pi }{2}} \right), \, (0,0)$ corresponds to the smallest buckling load, with a decrease of 59.37% (nickel). For the orthogonal stiffened PSC, at $(\theta_{x} ,\theta_{y} ) = \left( { - \frac{\pi }{2},0} \right), \, \left( {\frac{\pi }{2},0} \right), \, \left( {0,\frac{\pi }{2}} \right)$, the local minimum is captured. However, for certain engineering applications, sometimes the minimum value is desired instead of the maximum value, such as for the buckling behaviour for energy absorption in the prevention of fracture and crushing [70].

Fig. 7

Static buckling loads of the stiffened PSC

4.2 Wind-induced nonlinear forced vibration behaviour

The wind-induced nonlinear forced vibration behaviour of the stiffened PSC is comprehensively explored in this subsection. The diverse effects of the damping ratio, wind speed, nonlinear elastic foundation, thermal increment, oblique stiffeners, and pre-existing axial compression on the structural vibration response are examined. The fourth-order Runge–Kutta method is leveraged to solve Eq. (30) and obtain the time-deflection curve. The initial conditions are assumed to be $W(0) = 0, \, \frac{\partial W}{{\partial t}}(0) = 0$. The boundary conditions are deemed to be immovable. The coefficients of nonlinear elastic foundations indicate $k_{w} = 5 \times 10^{3} \;{\text{N/m}}^{3}$, $k_{p} = 5 \times 10^{3} {\text{N/m}}$, and $k_{n} = {5} \times {1}0^{3} \;{\text{N/m}}^{{5}}$.

The effect of the damping ratio on the nonlinear dynamic response of the stiffened PSC is shown in Fig. 8. The time-deflection curve fluctuates in a particular circle due to the wind impact. After the beginning of the wind load, the amplitude of deflection increases rapidly to the first local maximum. In the next stage, the deflection amplitude drops and then escalates similarly to the second local maximum. This circulation persists over time. Moreover, with the increase in the damping ratio, the amplitude of deflection decreases strongly, since the damping property depletes the potential energy of the system and suppresses the structure oscillation behaviour.

Fig. 8

The wind-induced nonlinear forced vibration of the stiffened PSC with diverse damping ratios

Figure 9 shows the influence of wind velocity on the nonlinear dynamic behaviour of the stiffened PSC. Four sets of wind speeds, namely $V_{w} = [13.9, \, 19.5, \, 24.3, \, 30.9]\;{\text{km/h}}$, are examined herein. It is observed that the vibration amplitude increases with increasing wind velocity.

Fig. 9

The wind-induced nonlinear forced vibration of the stiffened PSC with diverse wind speeds

The impact of pre-existing compressive loads on the nonlinear forced vibration of the stiffened PSC is illustrated in Fig. 10. The axial compression enhances the vibration behaviour, and intensifies the rising and falling time of the deflection amplitude.

Fig. 10

The wind-induced nonlinear forced vibration of the stiffened PSC with diverse pre-existing axial compressions

Figure 11 depicts the effect of the nonlinear elastic foundation parameters on the vibration attributes of the stiffened PSC. The rise of elastic foundation coefficients constrains the deflection amplitude. From the figure, the sharp increase in the Winkler elastic foundation modulus and nonlinear cubic stiffness, k_w and k_n, produces slight attenuation in the structure oscillation behaviour. In contrast, the Pasternak foundation stiffness, k_p, affords superior merit to suppress the vibration amplitude and strengthen the structural load bearing capability.

Fig. 11

The wind-induced nonlinear forced vibration of the stiffened PSC with diverse foundation coefficients

The influence of the thermal increment on the nonlinear vibration behaviour of the stiffened PSC is exhibited in Fig. 12. Three collections of temperature variance from surrounding circumstances, namely ΔT = [0, 20, 40°C], are incorporated to probe the dynamic characteristics. Under immovable boundary conditions, it is found that the ascent of temperature intensifies the amplitude of vibration. The explanation may be that the increase in temperature introduces extra axial stress within the structure, which is parallel to the stress triggered by external wind loads.

Fig. 12

The wind-induced nonlinear forced vibration of the stiffened PSC with diverse thermal increments

Figure 13a reflects the influence of oblique stiffeners on the nonlinear dynamic performance of the PSC. The stiffeners suggest an advantage in improving the structure stiffness and depressing the vibration behaviour. The maximum vibration deflection is demonstrated in Fig. 13b–f in terms of different stiffener angles and materials. The stiffener material of nickel and angle of $(\theta_{x} ,\theta_{y} ) = \left( { - \frac{\pi }{4},\frac{\pi }{4}} \right)$ illustrate the minimum deflection $W = 2.304 \times 10^{ - 6} {\text{m}}$, a reduction of 15.99% in comparison with the unstiffened PSC. A local minimum appears at a stiffener angle of $(\theta_{x} ,\theta_{y} ) = \left( {\frac{\pi }{4},\frac{\pi }{4}} \right)$. The specific amplitudes of the magnesium-, Al-, glass-, and copper-stiffened PSC $\left( {\theta_{x} = - \frac{\pi }{4},\theta_{y} = \frac{\pi }{4}} \right)$ are $W_{{{\text{Copper}}}} (2.415 \times 10^{ - 6} {\text{m}}) < W_{{{\text{Al}}}} (2.531 \times 10^{ - 6} {\text{m}}) < W_{{{\text{Glass}}}} (2.533 \times 10^{ - 6} {\text{m}}) < W_{{{\text{Magnesium}}}} (2.593 \times 10^{ - 6} {\text{m}})$.

Fig. 13

The wind-induced nonlinear forced vibration of the PSC with diverse stiffener angles and materials

4.3 Nonlinear dynamic biaxial buckling analysis

The nonlinear dynamic stability of the stiffened PSC under biaxial velocity impacts and movable boundary conditions is systematically investigated herein. Manifold effects of the damping ratio, impact speed, initial imperfection, elastic foundation parameters, thermal escalation, axial compression ratio, and oblique stiffeners on structure dynamic buckling behaviour are examined individually. The nonlinear dynamic biaxial buckling Eq. (35) is solved by applying the fourth-order Runge–Kutta method with initial conditions assumed as $W(0) = W_{0} , \, \frac{\partial W}{{\partial t}}(0) = 0$. The critical buckling load is captured based on the Budiansky–Roth criterion [68].

Figure 14 shows the influence of the damping ratio on the nonlinear dynamic buckling behaviour of the stiffened PSC. The longitudinal shortening of the plate can be determined by multiplying the impact speed by time. From Fig. 14, three disparate phases within the buckling response are visible, namely a slight fluctuation, swift growth, and ultimate structure vibration. For the dynamic compression load curve, there exist two distinctive stages, which are the linear pre-buckling and subsequent plate buckling oscillation. Moreover, the damping property exhausts the system energy and further suppresses fluctuation. In addition, the increase in the damping ratio enlarges the dynamic buckling load and enhances the structure impact resistance.

Fig. 14

The nonlinear dynamic biaxial buckling of the stiffened PSC with various damping ratios

The effect of impact speed on the nonlinear dynamic buckling characteristics of the stiffened PSC is revealed in Fig. 15. Three sets of impact loading rates, namely $v = 0.001 \times a\;{\text{m/s}}, \, 0.002 \times a\;{\text{m/s}}, \, 0.003 \times a\;{\text{m/s}}$, are considered. The growth of velocity diminishes the slight fluctuation stage and enlarges the amplitude of deflection. In addition, a greater impact speed produces an increase in the buckling load accompanied by a shorter time of arrival.

Fig. 15

The nonlinear dynamic biaxial buckling of the stiffened PSC with various impact velocities

Figure 16 shows the impact of the initial imperfection on the nonlinear buckling response of the stiffened PSC. Three different initial imperfections, namely $W_{0} = 0.01 \times h, \, 0.001 \times h, \, 0.0001 \times h$, are considered in this research. The ubiquitous initial flaws undermine the plate stiffness and impact carrying capacity. From the figure, it is discovered that the growth of the initial imperfection shortens the slight fluctuation stage and advances the buckling onset time. Moreover, the rise of the initial imperfection also reduces the dynamic buckling load.

Fig. 16

The nonlinear dynamic biaxial buckling of the stiffened PSC with various initial imperfections

The influence of nonlinear elastic foundation parameters on the dynamic buckling behaviour of the stiffened PSC is shown in Fig. 17. It is noted that the deflection amplitude declines due to the benefit of elastic foundations. Furthermore, the increase in elastic foundation coefficients enlarges the buckling load, extends the buckling time, and improves the structure impact resistance. In addition, the Pasternak shear layer foundation stiffness provides a more prominent impact than the Winkler foundation modulus and nonlinear cubic stiffness, as the Pasternak foundation constrains the transverse deflection and suppresses the vibration amplitude.

Fig. 17

The nonlinear dynamic biaxial buckling of the stiffened PSC with various foundation parameters

Figure 18 suggests the effect of thermal variation on the nonlinear dynamic buckling characteristics of the stiffened PSC. Three cases of thermal alterations, namely ΔT = [0, 10, 23.85°C], are studied herein. The escalation of temperature prolongs the slight fluctuation stage dramatically, further delays the buckling time, as well as increases the buckling load. This is because, under movable boundary conditions, the temperature rise increases the plate elongation and tension force, which is contrary to the effect of compressive impact.

Fig. 18

The nonlinear dynamic biaxial buckling of the stiffened PSC with various thermal increments

The effect of the axial compression ratio on the nonlinear buckling response of the stiffened PSC is depicted in Fig. 19. Under biaxial compressive impacts, the slight fluctuation stage shortens. In addition, the enlargement of the compression ratio intensifies the buckling deflection and advances the buckling occurrence time.

Fig. 19

The nonlinear dynamic biaxial buckling of the stiffened PSC with various compression ratios

Figure 20 shows the influence of oblique stiffeners on the nonlinear dynamic buckling behaviour of the PSC. The stiffeners advantageously enhance the buckling load and structural stiffness. The greatest improvement is observed with the nickel stiffener material compared with the other selected composites. Under biaxial velocity impact loading schemes, the axial compressive displacement is proportional to time. Thus, Fig. 20b can be recognized as the load-axial displacement curve. To maintain the same compression displacement, the axial stress $p_{x}$ of the stiffened PSC is much higher than that of the unreinforced plate, which results in an increase in the buckling load and advance of the buckling time, as illustrated in Fig. 20b.

Fig. 20

The nonlinear dynamic biaxial buckling of the PSC with various stiffener materials

The effect of the stiffener angles on the nonlinear dynamic buckling characteristics of the stiffened PSC is reported in Fig. 21. The peaks of buckling load along the x- and y-axes are captured at the stiffener angles of $(\theta_{x} ,\theta_{y} ) = (0,0)$ and $(\theta_{x} ,\theta_{y} ) = \left( {\frac{\pi }{2},\frac{\pi }{2}} \right)$. For the present biaxial loading regimes with fixed impact speeds $(\alpha_{v} = 0.5)$, the dominant compression is anticipated in the x direction. As a result, a higher compressive force accelerates the onset time of buckling and the longest buckling time is obtained at the stiffener angle of $(\theta_{x} ,\theta_{y} ) = \left( {\frac{\pi }{2},\frac{\pi }{2}} \right)$.

Fig. 21

The nonlinear biaxial buckling of the stiffened PSC with various stiffener angles

4.4 Influence of the active layer thickness on mechanical performance

Since the active layer chiefly mediates the photovoltaic performance of the PSC, much attention has been devoted to unveiling the influence of its thickness on efficiency and consequent alterations for PCE optimization. From the aforementioned discussion, the operating performance of the PSC depends strongly on its mechanical attributes and dynamic behaviour. Unfortunately, investigations of the influence on the mechanical behaviour have been rare. Hence, the detailed effects of active layer thickness on mechanical characteristics and device disbursement are revealed in this subsection in connection with the PCE.

Considering the work in [54], an experimental PSC with 14.05% efficiency is built, and the optimal PCE is predicted. The PSC parameters are the same as those in Sect. 4 except for the thicknesses of the perovskite and mesoporous layers. These two active layers are the most crucial parts for the efficiency of the whole device because the majority of electron generation and recombination takes place in these layers. In this study, the thickness of the perovskite layer is varied first, while the thickness of the mesoporous layer remains consistent, and vice versa. For the sake of comparison, the following non-dimensional thicknesses of the perovskite and mesoporous layer are introduced, which represent the thickness ratio between the active layer and the experimental PSC.

$$ h_{p}^{*} = \frac{{h_{p} }}{h}, \, h_{m}^{*} = \frac{{h_{m} }}{h} $$

(38)

where $h_{p}$ denotes the thickness of the perovskite layer, ranging from 25 to 400 nm, and $h_{m}$ represents the thickness of the mesoporous layer within the range of 50–500 nm.

The variations of natural frequency, static buckling load, nonlinear forced vibration characteristics, and dynamic buckling behaviour of the PSC in terms of different thicknesses of the perovskite and mesoporous layer are manifested in Figs. 22, 23, 24, 25 and 26. With increasing perovskite and mesoporous layer thickness, the natural frequency, static buckling load, and amplitude of vibration decrease. The growth of the active layer thickness also shortens the slight fluctuation stage within the dynamic buckling response and further decreases the buckling load with a shorter time of arrival.

Fig. 22

Natural frequencies of the PSC with different non-dimensional thicknesses of the perovskite and mesoporous layers

Fig. 23

Static critical buckling loads of the PSC with different non-dimensional thicknesses of the perovskite and mesoporous layers

Fig. 24

The wind-induced nonlinear forced vibration of the PSC with different non-dimensional thicknesses of the perovskite and mesoporous layers

Fig. 25

The nonlinear dynamic biaxial buckling of the PSC with different non-dimensional thicknesses of the perovskite layer

Fig. 26

The nonlinear dynamic biaxial buckling of the PSC with different non-dimensional thicknesses of the mesoporous layer

The potential estimated PCE is discovered in [54] by adapting the mesoporous and perovskite layer thicknesses concurrently. The anticipated peak efficiency of 14.4% is predicted at the perovskite layer thickness of 200 nm and mesoporous layer thickness of 90 nm. Deviation from this thickness is predicted to result in a gradual attenuation from the optimal photovoltaic performance. Moreover, the mechanical behaviours vary in a simple and monotonic way. The increase in mesoporous and perovskite layer thickness decreases the natural frequency, static buckling load, vibration amplitude, and dynamic buckling load and shortens the buckling time, which further illuminates the real-world application of PSC devices. For example, it is appropriate to intensify the vibration behaviour for solar purging products [12]. However, for a solar structure designed against wind or impacts, it is critical to diminish the vibration response and take precautions against buckling failure. In addition, the rise of the two active layer thicknesses also increases the ingredient cost and yields toxicity issues within the device manufacturing, implementation, and disposal process, as lead constitutes the main component [6]. Therefore, for the purpose of achieving optimal device efficiency and mechanical performance as well as structure cost, it is pivotal to enhance the PCE and mechanical characteristics of realistic products while lowering material expenditure.

5 Conclusion

The mechanical performance and dynamic stability of the novel PSC under practical impacts are part and parcel of ensuring the operating capability and service time of real-life solar devices. To improve the structural capacity of the ultra-thin PSC, oblique stiffeners have been introduced as reinforcements against external impacts. This paper investigates the free vibration, nonlinear forced vibration, and static and dynamic stability of the stiffened PSC under biaxial impacts. Numerous effects of the damping ratio, thermal variance, wind load, compression speed, elastic foundation, initial imperfection, axial compression ratio, oblique stiffeners, and active layer thickness on structure performance are examined through the parametric study. The present study fits the prospering journey in the practical design and commercial deployment of PSC light-harvesting products with intensified structural stability against impacts and safety. Some main conclusions can be outlined:

• 1. The nonlinear elastic foundation notably improves the dynamic behaviour and impact resistance of the PSC. The increase in elastic foundation coefficients reduces the vibration amplitude, enlarges the natural frequency and static and dynamic buckling load, and extends the buckling time. In addition, the Pasternak shear layer foundation exhibits a remarkable influence, which can be exploited to suppress the vibration response and avoid buckling failure.

• 2. The stiffeners provide advantages in enhancing the structural stiffness and impact carrying capability of the PSC, with improvements in the natural frequency, static and dynamic buckling load, as well as attenuation of vibration response. Among the selected materials, the nickel stiffener presents the best mechanical performance. The stiffener angle of $(\theta_{x} ,\theta_{y} ) = \left( { - \frac{\pi }{4},\frac{\pi }{4}} \right)$ illustrates the maximum static buckling load and minimum vibration amplitude.

• 3. For the movable boundary conditions, increasing the temperature produces the axial tension stress and further increases the dynamic buckling load as well as the buckling time. For immovable boundary conditions, increasing the temperature intensifies the vibration amplitude, as it results in the opposite compression because of the restriction on plate expansion.

• 4. Shaking the serviceability of structures, inevitable initial imperfections impair the dynamic performance of the PSC. The increase in the initial imperfection shortens the buckling time and decreases the buckling load. Optimizing the manufacturing technique and fine-tuning the composite quality represents a viable solution for decreasing imperfections and strengthening the structure capacity.

• 5. Increasing the active layer thickness reduces the natural frequency, static buckling load, vibration amplitude, dynamic buckling load, and buckling time.

• 6. It is noted that the characterization of the abovementioned effects and parameters should be cautious and based on real-world PSC devices, such as the preference for utilization or suppression of vibration and buckling behaviour, the balance between mechanical performance and efficiency and overall cost.

For future work in this area, first, the present study can be extended to advanced composite materials and structures. Examination of their advantages in the intrinsic property and structure performance under different loadings should be implemented. Second, future research can extend the present study to realistic advanced solar structures. The practical engineering application in the real environment should be investigated, and different effects on the operating performance of the structure should be discussed. Third, the analysis of long-term serviceability and lifetime for advanced solar structures can be performed in future studies.

Appendix

See Appendix Tables

Table 8 Notations and descriptions of equation variables

8 and

Table 9 List of abbreviations

9.

$$ \begin{aligned} (\overline{{I_{ij} }} ,\overline{{J_{ij} }} ,\overline{{K_{ij} }} ) = \sum\limits_{l = 1}^{k} {\int_{{z_{l} }}^{{z_{l + 1} }} {(C_{ij} )_{l} (1,z,z^{2} )dz} } ,i,j = 1,2,6 \\ & I_{11} = \overline{{I_{11} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\cos^{4} \theta_{x} + \cos^{4} \theta_{y} ), \, \\ & I_{12} = \overline{{I_{12} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \\ & I_{22} = \overline{{I_{22} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\sin^{4} \theta_{x} + \sin^{4} \theta_{y} ), \, \\ & I_{16} = \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\sin \theta_{x} \cos^{3} \theta_{x} + \sin \theta_{y} \cos^{3} \theta_{y} ), \\ & I_{26} = \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\sin^{3} \theta_{x} \cos \theta_{x} + \sin^{3} \theta_{y} \cos \theta_{y} ), \, \\ & I_{66} = \overline{{I_{66} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \\ & J_{11} = \overline{{J_{11} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\cos^{4} \theta_{x} + \cos^{4} \theta_{y} ), \, \\ & J_{12} = \overline{{J_{12} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \, \\ & J_{22} = \overline{{J_{22} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\sin^{4} \theta_{x} + \sin^{4} \theta_{y} ), \\ & J_{16} = \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\sin \theta_{x} \cos^{3} \theta_{x} + \sin \theta_{y} \cos^{3} \theta_{y} ), \\ & J_{26} = \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\sin^{3} \theta_{x} \cos \theta_{x} + \sin^{3} \theta_{y} \cos \theta_{y} ), \, \\ & J_{66} = \overline{{J_{66} }} + \frac{{E_{s} h_{s} d_{s} }}{{s_{s} }}\left( {\frac{{h + h_{s} }}{2}} \right)(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \\ \end{aligned} $$

$$ \begin{aligned} K_{11} = \overline{{K_{11} }} + \frac{{E_{s} I_{s} }}{{s_{s} }}(\cos^{4} \theta_{x} + \cos^{4} \theta_{y} ), \hfill \\ K_{12} = \overline{{K_{12} }} + \frac{{E_{s} I_{s} }}{{s_{s} }}(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \hfill \\ K_{22} = \overline{{K_{22} }} + \frac{{E_{s} I_{s} }}{{s_{s} }}(\sin^{4} \theta_{x} + \sin^{4} \theta_{y} ), \hfill \\ K_{16} = \frac{{E_{s} I_{s} }}{{s_{s} }}(\sin \theta_{x} \cos^{3} \theta_{x} + \sin \theta_{y} \cos^{3} \theta_{y} ), \hfill \\ K_{26} = \frac{{E_{s} I_{s} }}{{s_{s} }}(\sin^{3} \theta_{x} \cos \theta_{x} + \sin^{3} \theta_{y} \cos \theta_{y} ), \hfill \\ K_{66} = \overline{{K_{66} }} + \frac{{E_{s} I_{s} }}{{s_{s} }}(\sin^{2} \theta_{x} \cos^{2} \theta_{x} + \sin^{2} \theta_{y} \cos^{2} \theta_{y} ), \hfill \\ I_{s} = \frac{{d_{s} h_{s}^{3} }}{12} + h_{s} d_{s} \left( {\frac{{h + h_{s} }}{2}} \right)^{2} , \hfill \\ I_{11}^{*} { = }\frac{{I_{26}^{2} - I_{22} I_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{12}^{*} = \frac{{ - I_{16} I_{26} + I_{12} I_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{16}^{*} = \frac{{I_{16} I_{22} - I_{12} I_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{11}^{*} = \frac{{ - I_{26}^{2} J_{11} + I_{22} I_{66} J_{11} + I_{16} I_{26} J_{12} - I_{12} I_{66} J_{12} - I_{16} I_{22} J_{16} + I_{12} I_{26} J_{16} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{12}^{*} = \frac{{ - I_{26}^{2} J_{12} + I_{22} I_{66} J_{12} + I_{16} I_{26} J_{22} - I_{12} I_{66} J_{22} - I_{16} I_{22} J_{26} + I_{12} I_{26} J_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{16}^{*} = \frac{{ - I_{26}^{2} J_{16} + I_{22} I_{66} J_{16} + I_{16} I_{26} J_{26} - I_{12} I_{66} J_{26} - I_{16} I_{22} J_{66} + I_{12} I_{26} J_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ \end{aligned} $$

$$ \begin{aligned} I_{17}^{*} = \frac{{(I_{26}^{2} - I_{22} I_{66} )\overline{{I_{11} }} + ( - I_{16} I_{26} + I_{26}^{2} + I_{12} I_{66} - I_{22} I_{66} )\overline{{I_{12} }} + ( - I_{16} I_{26} + I_{12} I_{66} )\overline{{I_{22} }} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{21}^{*} { = }\frac{{ - I_{16} I_{26} + I_{12} I_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{22}^{*} { = }\frac{{I_{16}^{2} - I_{11} I_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{26}^{*} { = }\frac{{ - I_{12} I_{16} + I_{11} I_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{21}^{*} = \frac{{I_{16} I_{26} J_{11} - I_{12} I_{66} J_{11} - I_{16}^{2} J_{12} + I_{11} I_{66} J_{12} + I_{12} I_{16} J_{16} - I_{11} I_{26} J_{16} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{22}^{*} = \frac{{I_{16} I_{26} J_{12} - I_{12} I_{66} J_{12} - I_{16}^{2} J_{22} + I_{11} I_{66} J_{22} + I_{12} I_{16} J_{26} - I_{11} I_{26} J_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{26}^{*} = \frac{{I_{16} I_{26} J_{16} - I_{12} I_{66} J_{16} - I_{16}^{2} J_{26} + I_{11} I_{66} J_{26} + I_{12} I_{16} J_{66} - I_{11} I_{26} J_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ \end{aligned} $$

$$ \begin{aligned} I_{27}^{*} = \frac{{( - I_{16} I_{26} + I_{12} I_{66} )\overline{{I_{11} }} + (I_{16}^{2} - I_{16} I_{26} - I_{11} I_{66} + I_{12} I_{66} )\overline{{I_{12} }} + (I_{16}^{2} - I_{11} I_{66} )\overline{{I_{22} }} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{61}^{*} { = }\frac{{I_{16} I_{22} - I_{12} I_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{62}^{*} { = }\frac{{ - I_{12} I_{16} + I_{11} I_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{66}^{*} { = }\frac{{I_{12}^{2} - I_{11} I_{22} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{61}^{*} { = }\frac{{ - I_{16} I_{22} J_{11} + I_{12} I_{26} J_{11} + I_{12} I_{16} J_{12} - I_{11} I_{26} J_{12} - I_{12}^{2} J_{16} + I_{11} I_{22} J_{16} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{62}^{*} { = }\frac{{ - I_{16} I_{22} J_{12} + I_{12} I_{26} J_{12} + I_{12} I_{16} J_{22} - I_{11} I_{26} J_{22} - I_{12}^{2} J_{26} + I_{11} I_{22} J_{26} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ J_{66}^{*} { = }\frac{{ - I_{16} I_{22} J_{16} + I_{12} I_{26} J_{16} + I_{12} I_{16} J_{26} - I_{11} I_{26} J_{26} - I_{12}^{2} J_{66} + I_{11} I_{22} J_{66} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }}, \hfill \\ I_{67}^{*} = \frac{{(I_{16} I_{22} - I_{12} I_{26} )\overline{{I_{11} }} + (I_{16} I_{22} + I_{11} I_{26} - I_{12} (I_{16} + I_{26} ))\overline{{I_{12} }} + ( - I_{12} I_{16} + I_{11} I_{26} )\overline{{I_{22} }} }}{{I_{16}^{2} I_{22} - 2I_{12} I_{16} I_{26} + I_{11} I_{26}^{2} + I_{12}^{2} I_{66} - I_{11} I_{22} I_{66} }} \hfill \\ \end{aligned} $$

$$ \begin{aligned} \overline{{I_{11}^{*} }} = J_{11} I_{11}^{*} + J_{12} I_{21}^{*} + J_{16} I_{61}^{*} , \hfill \\ \overline{{I_{12}^{*} }} = J_{11} I_{12}^{*} + J_{12} I_{22}^{*} + J_{16} I_{62}^{*} , \hfill \\ \overline{{I_{16}^{*} }} = J_{11} I_{16}^{*} + J_{12} I_{26}^{*} + J_{16} I_{66}^{*} \hfill \\ \overline{{I_{21}^{*} }} = J_{12} I_{11}^{*} + J_{22} I_{21}^{*} + J_{26} I_{61}^{*} , \hfill \\ \overline{{I_{22}^{*} }} = J_{12} I_{12}^{*} + J_{22} I_{22}^{*} + J_{26} I_{62}^{*} , \hfill \\ \overline{{I_{26}^{*} }} = J_{12} I_{16}^{*} + J_{22} I_{26}^{*} + J_{26} I_{66}^{*} \hfill \\ \overline{{I_{61}^{*} }} = J_{16} I_{11}^{*} + J_{26} I_{21}^{*} + J_{66} I_{61}^{*} , \hfill \\ \overline{{I_{62}^{*} }} = J_{16} I_{12}^{*} + J_{26} I_{22}^{*} + J_{66} I_{62}^{*} , \hfill \\ \overline{{I_{66}^{*} }} = J_{16} I_{16}^{*} + J_{26} I_{26}^{*} + J_{66} I_{66}^{*} \hfill \\ \overline{{J_{11}^{*} }} = J_{11} J_{11}^{*} + J_{12} J_{21}^{*} + J_{16} J_{61}^{*} + K_{11} , \hfill \\ \overline{{J_{12}^{*} }} = J_{11} J_{12}^{*} + J_{12} J_{22}^{*} + J_{16} J_{62}^{*} + K_{12} , \hfill \\ \end{aligned} $$

$$ \begin{aligned} \overline{{J_{16}^{*} }} = J_{11} J_{16}^{*} + J_{12} J_{26}^{*} + J_{16} J_{66}^{*} + K_{16} , \hfill \\ \overline{{J_{21}^{*} }} = J_{12} J_{11}^{*} + J_{22} J_{21}^{*} + J_{26} J_{61}^{*} + K_{12} , \hfill \\ \overline{{J_{22}^{*} }} = J_{12} J_{12}^{*} + J_{22} J_{22}^{*} + J_{26} J_{62}^{*} + K_{22} , \hfill \\ \overline{{J_{26}^{*} }} = J_{12} J_{16}^{*} + J_{22} J_{26}^{*} + J_{26} J_{66}^{*} + K_{26} , \hfill \\ \overline{{J_{61}^{*} }} = J_{16} J_{11}^{*} + J_{26} J_{21}^{*} + J_{66} J_{61}^{*} + K_{16} , \hfill \\ \overline{{J_{62}^{*} }} = J_{16} J_{12}^{*} + J_{26} J_{22}^{*} + J_{66} J_{62}^{*} + K_{26} , \hfill \\ \overline{{J_{66}^{*} }} = J_{16} J_{16}^{*} + J_{26} J_{26}^{*} + J_{66} J_{66}^{*} + K_{66} , \hfill \\ \overline{{I_{17}^{*} }} { = }J_{11} I_{17}^{*} + J_{12} I_{27}^{*} + J_{16} I_{67}^{*} - (\overline{{J_{11} }} + \overline{{J_{12} }} ), \hfill \\ \overline{{I_{27}^{*} }} { = }J_{12} I_{17}^{*} + J_{22} I_{27}^{*} + J_{26} I_{67}^{*} - (\overline{{J_{12} }} + \overline{{J_{22} }} ), \hfill \\ \overline{{I_{67}^{*} }} { = }J_{16} I_{17}^{*} + J_{26} I_{27}^{*} + J_{66} I_{67}^{*} , \hfill \\ \lambda_{11} { = }\frac{{I_{22}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{1}{ab} - \frac{{I_{12}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha_{v} }}{ab}, \hfill \\ \lambda_{21} { = } - \frac{{I_{21}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{1}{ab} + \frac{{I_{11}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha_{v} }}{ab}, \hfill \\ \lambda_{12} { = }\frac{{ - I_{22}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\left( {\frac{4}{ab\alpha }\beta F_{3} I_{11}^{*} + \frac{4}{ab\beta }\alpha F_{3} I_{12}^{*} + \frac{4}{ab}I_{16}^{*} F_{4} - J_{11}^{*} \alpha \frac{4}{ab\beta } - J_{12}^{*} \beta \frac{4}{ab\alpha }} \right) \hfill \\ + \frac{{I_{12}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\left( {\frac{4}{ab\alpha }\beta F_{3} I_{21}^{*} { + }\frac{4}{ab\beta }\alpha F_{3} I_{22}^{*} { + }\frac{4}{ab}I_{26}^{*} F_{4} - J_{21}^{*} \alpha \frac{4}{ab\beta } - J_{22}^{*} \beta \frac{4}{ab\alpha }} \right), \hfill \\ \lambda_{22} { = }\frac{{I_{21}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\left( {\frac{4}{ab\alpha }\beta F_{3} I_{11}^{*} + \frac{4}{ab\beta }\alpha F_{3} I_{12}^{*} + \frac{4}{ab}I_{16}^{*} F_{4} - J_{11}^{*} \alpha \frac{4}{ab\beta } - J_{12}^{*} \beta \frac{4}{ab\alpha }} \right) \hfill \\ \quad - \frac{{I_{11}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\left( {\frac{4}{ab\alpha }\beta F_{3} I_{21}^{*} { + }\frac{4}{ab\beta }\alpha F_{3} I_{22}^{*} { + }\frac{4}{ab}I_{26}^{*} F_{4} - J_{21}^{*} \alpha \frac{4}{ab\beta } - J_{22}^{*} \beta \frac{4}{ab\alpha }} \right), \hfill \\ \lambda_{13} { = }\frac{{ - I_{22}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha^{2} }}{8} + \frac{{I_{12}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\beta^{2} }}{8}, \, \hfill \\ \lambda_{23} { = }\frac{{I_{21}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha^{2} }}{8} - \frac{{I_{11}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\beta^{2} }}{8}, \hfill \\ \lambda_{14} { = }\frac{{ - I_{22}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha^{2} }}{4} + \frac{{I_{12}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\beta^{2} }}{4}, \, \hfill \\ \lambda_{24} { = }\frac{{I_{21}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\alpha^{2} }}{4} - \frac{{I_{11}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}\frac{{\beta^{2} }}{4}, \hfill \\ \lambda_{15} { = }\frac{{I_{22}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}I_{17}^{*} - \frac{{I_{12}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}I_{27}^{*} , \, \hfill \\ \lambda_{25} { = } - \frac{{I_{21}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}I_{17}^{*} + \frac{{I_{11}^{*} }}{{I_{12}^{*} I_{21}^{*} - I_{11}^{*} I_{22}^{*} }}I_{27}^{*} \hfill \\ \end{aligned} $$