Analysing dynamic deep stall recovery using a nonlinear frequency approach

Abstract

Based on bifurcation theory, nonlinear frequency response analysis is a recent development in the field of flight dynamics studies. Here, we consider how this method can be used to inform us on how to devise the control input such that the system transitions from an undesirable equilibrium solution—an aircraft deep stall solution in our case—to a desirable solution. We show that it is still possible to induce a large-amplitude oscillation via harmonic forcing of the pitch control device and escape the otherwise unrecoverable deep stall, despite very little control power available in such a high angle-of-attack flight condition. The forcing frequencies that excite these resonances are reflected as asymptotically unstable solutions using bifurcation analysis and Floquet theory. Due to the softening behaviour observed in the frequency response, these unstable (divergent) solutions have slightly lower frequencies than the value predicted using linear analysis. Subharmonic resonances are also detected, which are reflected in the time-domain unforced responses. These nonlinear phenomena show strong dependency on the forcing/perturbation amplitude and result in complex dynamics that can impede recovery if the existing procedures are followed. The proposed method is shown to be a useful tool for nonlinear flight dynamics analysis as well as to complement the rather thin literature on deep stall analysis—a topic of relevance for recent research on unconventional landing techniques in unmanned aerial vehicles. A full description of the aircraft model used, the unstable F-16 fighter jet, is provided in the appendix.

1 Introduction

Aircraft can potentially encounter flight conditions in which rich and nonlinear dynamics cause sudden and dangerous responses, especially in high angles-of-attack or sideslip conditions. In order to fully understand these behaviours, bifurcation analysis has regularly been employed in the past four decades in both academia [1,2,3,4] and the industry [5] thanks to its ability to characterise many important phenomena in flight dynamics and control analysis, such as spins, stall, and wing rock. Recent developments in the field saw the use of a harmonic forcing term to generate a ‘nonlinear Bode plot’ (i.e. nonlinear frequency analysis). The advantage of this approach is that it facilitates assessments of the non-stationary nonlinear elements like sub/super-harmonic resonances [6] and actuator rate limiting [7], which only become evident during a manoeuvre where the pilot input is not constant. As a result, the method opens up another dimension of nonlinear analysis that can be of great interests for researchers in flight dynamics and control analysis.

In this paper, nonlinear frequency response is employed to devise a recovery manoeuvre from deep stall—a dangerous condition in which the aircraft is locked into a high angle-of-attack attitude that results in a steep descending trajectory. In serious cases, this descending trajectory is maintained even with the nose horizontal or pointing upward (i.e. the aircraft falls belly-first—see Fig. 1b). A deep stall is deemed unrecoverable (locked-in) when there is insufficient pitch control authority to bring the nose down and reduce the angle-of-attack. This problem has resulted in many accidents of early T-tail airliners—a design that is especially susceptible to deep stall [8]. Although there are many successful safety measures in use to prevent excursion into the deep stall region, most commonly via stick shaker & stick pusher [8] and digital angle-of-attack limiter in full-authority fly-by-wire systems [9, 10], research into deep stall recovery methods are few and of limited scope. These studies either involve simplified flight dynamics models [11,12,13,14,15] or empirical methods [10, 16], making it hard to determine a safe and consistent procedure to guarantee recovery. Moreover, recent research into advanced landing techniques for small unmanned aerial vehicles involves deliberately bringing the aircraft into a deep stall to minimise the landing distance [17,18,19]. These developments emphasise the need to improve our understanding of the flight characteristics in the deep stall regime. Future studies on this topic can also benefit from recent data published by NASA [20,21,22], which provides high-fidelity flight dynamics modelling of a hypothetical T-tail passenger aircraft as part of the global effort to reduce airliner loss-of-control incidents [23, 24].

Fig. 1

A T-tail aircraft in normal flight a and deep stall b*. In panel b, the horizontal tailplane is in the wake of the stalled wing as indicated by the shading. This leads to a significant reduction in pitch control authority and can cause an unrecoverable deep stall

Previous works have indicated that it is possible to rock the aircraft’s nose to gain momentum, making it possible to gain some pitch control and push the nose down below the critical angle-of-attack [10, 13, 16]. We therefore hypothesise and then demonstrate that a nonlinear frequency-domain analysis can provide further insights into this problem to systematically derive a successful recovery manoeuvre. A brief explanation of the deep stall problem is provided in Sect. 2, along with a description of the aircraft model used for this study. Previous investigations on potential recovery methods are discussed in Sect. 3. Then, Sect. 4–5 describes the proposed method, followed by concluding remarks in Sect. 6. All bifurcation analysis was carried out using the Dynamical Systems Toolbox [25], which is a MATLAB/Simulink implementation of the numerical continuation software AUTO [26].

2 Deep stall prediction

The conventional way to predict a deep stall is to examine the relationship between the pitching moment coefficient $C_{{\text{M}}}$ and angle-of-attack $\alpha$. Referring to the pitch rate equation $\dot{q} = \frac{1}{2}\rho V^{2} Sc\frac{{C_{{\text{M}}} }}{{I_{y} }}$, an aircraft in equilibrium (trimmed) will have zero pitch rate ($\dot{q}$ = 0), thereby requiring $C_{{\text{M}}}$ = 0 (see the appendix for the full set of equations of motion and definition of terms). Because $C_{{\text{M}}}$ is a function of angle of attack, a statically stable trim point has $\frac{{\partial C_{{\text{M}}} }}{\partial \alpha } < 0$. Figure 2 shows an example $C_{{\text{M}}} \left( \alpha \right)$ plot of a typical T-tail design. The third trim point at 51° angle-of-attack is stable. If there is not enough pitch control authority to bring the nose down, the aircraft will be stuck in this high $\alpha$ condition, leading to an unrecoverable deep stall.

Fig. 2

Typical pitching moment coefficient plot for the T-tail configuration. Negative slope indicates positive stability

Unrecoverable deep stall due to insufficient pitch control power is usually linked to the following features:

• A T-tail configuration, which puts the pitch control device, such as elevator or stabilator (all-moving tailplane), in the wake of the wing at high angles-of-attack and renders them ineffective (see Fig. 1b).

• An aft centre of gravity, which reduces the elevator/stabilator moment arm. This design is usually found in statically unstable fighter aircraft for improved manoeuvrability, controllability in the presence of shock waves, and reducing trim drag.

To examine how bifurcation analysis can be used to develop recovery manoeuvres from deep stall, this paper considers the dynamics of the F-16 fighter jet. This model is suitable for our analysis because it is unstable at low and stable at high angles-of-attack, meaning that the aircraft has a natural tendency to pitch up into a deep stall when flown manually. Its open-loop dynamics is presented in the rest of this section to provide a basic overview of the airframe under consideration. Using aerodynamic data from [10], we constructed a fourth-order version of the aircraft with the four relevant longitudinal states $\alpha$ (angle-of-attack), $V$ (velocity), $q$ (pitch rate), and $\theta$ (pitch angle), and three inputs $\delta_{{\text{s}}}$ (stabilator deflection), $T$ (thrust), and ${\text{CG}}$ (centre of gravity position), thereby restricting the motion to the longitudinal plane. The equations of motion and aerodynamic data tables for this reduced-order model are provided in the appendix. The use of secondary control surfaces such as leading edge devices, flaps, and speed brake is not considered for simplicity without loss of generality. We use a fixed thrust of 8,785 N and centre of gravity at 37.5% mean aerodynamic chord (MAC). At 30,000 feet altitude, this combination results in a trimmed level flight at Mach 0.6, which matches the most severe test cases done by NASA [10]. Pitch control is achieved using a pair of all-moving horizontal stabilator that can deflect up to 25° in both directions.

Neglecting the impact of change in altitude (and hence air density) on the dynamics of the system, equilibrium bifurcation analysis can be performed on the fourth-order aircraft model. Figure 3 shows the bifurcation diagram with the horizontal stabilator $\delta_{{\text{s}}}$ as the continuation parameter. A negative stabilator deflection corresponds to a nose-up command in a statically stable aircraft due to sign convention. From the angle-of-attack bifurcation diagram in Fig. 3a, it can be seen that the aircraft is statically unstable below 20° angle-of-attack. Normal operation in this regime therefore requires the use of a full-authority feedback controller (which usually limits the maximum $\alpha$ to 25° [10, 11]). There is also a branch of stable solutions at very high angles-of-attack (around 60°) that exists throughout the whole stabilator deflection range. Because this stable high $\alpha$ solution exists at full nose-down elevator (25°), a locked-in deep stall is possible.

Fig. 3

Bifurcation diagram: stabilator continuation. The pitch rate bifurcation diagram is not shown as all equilibrium solutions have $q$=0 deg/s. Solutions beyond ${\delta }_{s}$=25° were found using spline extrapolation to investigate the nature of the isola associated with point B

In this instance, there are actually two possible deep stall trajectories at $\delta_{{\text{s}}}$=25°. Figure 4 illustrates these two possible flight trajectories at deep stall. It can be seen that the aircraft converges to one of the two stable solutions that results in a steep descending trajectory at low speed (refer to the bifurcation diagram in Fig. 3b for the speed at equilibrium)—despite the combination of a slight nose-up attitude, full nose-down stabilator, and a constant thrust adequate for cruise at Mach 0.6 (182 m/s). The existence of the second branch at a slightly lower angle-of-attack of 47° makes recovery more challenging. The reason is that in normal operation with the full-authority flight control system active, the $\alpha$ limiter will detect that the maximum 25° limit has been exceeded and will continually try to push the nose down, thereby keeping the stabilator fixed at 25°. As seen from Fig. 3, two stable deep stall trim points exist at $\delta_{{\text{s}}}$ = 25°, so the aircraft has a high probability of being stuck in one of these two high-$\alpha$ descending trajectories. The pilot loses all command of the aircraft via the fly-by-wire control law in this situation, so direct open-loop control is required to recover from deep stall [10]. Past studies have also not revealed the second deep stall branch connected to point B [10, 11], potentially due to their inclusion of the leading edge device.

Fig. 4

Trajectories of two possible trimmed conditions at deep stall with max nose-down stabilator $({\delta }_{s}$=25°). The vertical axis $z$ is positive down due to sign convention. Aircraft not drawn to scale and are shown 5 s apart, indicating a rapid drop in altitude

The existence of these equilibrium trim points at deep stall can be verified by examining the pitching moment $C_{{\text{M}}} \left( \alpha \right)$ curves in Fig. 5. Noting that the pitching moment coefficient must be zero at equilibrium, there are two stable trim points at full nose-down stabilator ($\delta_{{\text{s}}}$= 25°): $\alpha$ = 47° and $\alpha$ = 57°, which confirms the prediction of deep stall by bifurcation analysis. Furthermore, the $C_{{\text{M}}}$ for ${\delta }_{s}$ = 25° is very close to zero for high angles-of-attack (above 40°), indicating that there is very limited pitch-down capability in this region.

Fig. 5

Pitching moment coefficients for three stabilator deflection values. Trim points exist where ${C}_{M}$=0. Negative slope indicates positive stability

Finally, the link between recoverability and centre of gravity placement is examined. The current deep stall is unrecoverable because the fold bifurcation labelled A in Fig. 3a lies beyond the stabilator deflection physical limit of 25°. Moving the centre of gravity forward will bring point A back within the elevator deflection range, making it possible to push the nose down below the very high $\alpha$ region. Using two-parameter continuation, we can verify this by computing the locus of the fold bifurcations labelled A and B in Fig. 3a as functions of stabilator deflection and centre of gravity position. Figure 6 shows that as the centre of gravity moves forward, the branch associated with point A drops below $\delta_{{\text{s}}}$=25° whereas the one linked to point B increases beyond the deflection limit, indicating that there is no locked-in deep stall for CG at 36.4% MAC or lower.

Fig. 6

Locus of the fold bifurcations labelled A and B in Fig. 3a, calculated using two-parameter continuation. Data beyond $\delta_{{\text{s}}}$=25° are spline-extrapolated

3 Issues with existing deep stall recovery methods

Although past studies have confirmed the existence of deep stall on the F-16 in both simulated [10] and real flights [16] as well as using equilibrium bifurcation analysis [11], their proposed recovery procedures are rather empirical and bring mixed results. A brief summary is provided in this section, along with a discussion on their effectiveness.

Nguyen et al. suggested that upon entering a deep stall, the pilot would observe the transient oscillation as the aircraft settles into the stable high-$\alpha$ trim and pump the stick at the same frequency as that oscillation [10]. The idea is that by matching the forcing input with aircraft’s natural rigid-body frequency, it would be possible to build up some momentum with the little control authority available to push the nose down. An earlier study by NASA on a simplified T-tailed airliner model [13] used a somewhat similar idea (referred to as ‘dynamic recovery’): the elevator is excited in a square wave pattern, which reverses direction when the pitch rate reaches zero. Both methods require close observation of the ensuing transient oscillation in order to match the forcing input with the aircraft’s frequency. In fact, it was noted in [10] that slow or unsuccessful recoveries were attributed to the difficulty of matching the input frequency. There is also the risk of the pilot not reacting fast enough to deep stall entry, meaning that the oscillation is already damped out by the time the pilot initiates the manoeuvre. Furthermore, it was not highlighted in the studies above that the frequency-domain dynamics of the aircraft at such high angles-of-attack is highly nonlinear. Depending on how the aircraft entered the deep stall condition, the ensuing oscillation may have different and varying frequencies, making it more challenging to observe the motion and provide a forcing term. Figure 7 illustrates this point by showing the nonlinear simulations of the open-loop F-16 trimmed at $\delta_{{\text{s}}}$ = 0° ($\alpha$ = 59°) responding to different levels of angle-of-attack perturbation. For a small perturbation of 4°, the response resembles the linear simulation (not shown), and its fast Fourier transform in Fig. 8b indicates a single resonant frequency of 1.35 rad/s. For larger perturbations, Fig. 7 show that their responses are now highly nonlinear as indicated by the non-symmetric oscillation about the trim point and the varying oscillation frequencies. In fact, Fig. 7b shows that after the transient motions have damped out, the ensuing small-amplitude oscillations are not lined up with each other unlike in a linear system. The existence of multiple frequency components can also be highlighted by the fast Fourier transform of time history data. Figure 8c and d indicates not only the additional harmonics but also a reduction in the natural frequency as the perturbation amplitude increases, which is indicative of a softening forced system from a frequency analysis perspective. All of this highlights the nonlinear nature of the dynamics at such a high angle-of-attack. As the oscillation frequency is not constant, the way the aircraft enters a deep stall will affect the ensuing response and consequently the forcing input required from the pilot. If a non-optimal frequency is chosen by the pilot, the recovery process will be more challenging or even unsuccessful [10, 13].

Fig.7

Simulated responses to angle-of-attack perturbation. ${\Delta }\alpha_{0}$ is the perturbation amplitude. The blue line corresponds to the trimmed (unperturbed) aircraft. Both panels show the same sets of simulations but at different time intervals

Fig. 8

Fast fourier transforms of the $\alpha$-perturbed time histories. Perturbation of extremely small amplitude in a is provided as the reference for a linear-like response. The frequency components below 0.1 rad/s can be attributed to the damping and should be ignored

A different recovery procedure was proposed in [11]. It was found that at maximum thrust, the stable trim point at full nose-down stabilator becomes unstable. However, a time history in [11] shows that it takes 60 s of max thrust to take the aircraft out of the deep stall region (i.e. the unstable mode’s divergence is very slow). The method also demands that the engine produces maximum thrust throughout the entire manoeuvre. This is not necessarily a valid assumption as most engines will experience a noticeable performance reduction at such high angles-of-attack. In addition, due to the lack of a publicly-available high-fidelity model of the F-16’s engine, we are unable to further pursue this method.

To conclude, forcing the pitch control device to rock the aircraft’s nose and generate some nose-down momentum is a promising approach for deep stall recovery. The challenges encountered by previous studies on this method have been highlighted, mostly due to high pilot workload and the additional harmonic components in the aircraft’s responses. Nonlinear frequency analysis can provide further insights into the issue. This is discussed in the next section.

4 Nonlinear frequency analysis and the proposed recovery procedure

Nonlinear forced analysis is common in the applied maths community [27,28,29]. However, this approach has only recently been fully exploited in a flight dynamics context [6, 7] after some preliminary works from the 1990s [30,31,32] and 2000s [33]. A summary of the method is now provided. In order to replicate the stick pumping action in [10], we set the stabilator deflection to $\delta_{{\text{s}}} = A\sin \omega t$, where $A$ is the forcing amplitude in deg and $\omega$ is the forcing frequency in rad/s. Numerical continuation requires that all state equations are autonomous (no $t$ on the right-hand side). This condition can be satisfied by replacing $\mathrm{sin}\omega t$ with state ${x}_{5}$ defined as:

$$ \dot{x}_{5} = x_{5} + \omega x_{6} - x_{5} \left( {x_{5}^{2} + x_{6}^{2} } \right) $$

(1)

$$ \dot{x}_{6} = - \omega x_{5} + x_{6} - x_{6} \left( {x_{5}^{2} + x_{6}^{2} } \right) $$

(2)

It can be shown that $x_{5} = \sin \omega t$ and $x_{6} = \cos \omega t$ are asymptotically stable solutions of Eqs. (1–2) (see appendix of [34] for proof). The ensuing oscillation may be nonlinear (non-sinusoidal), thereby containing multiple harmonics like the example shown in Fig. 9. In such instances, we approximate the gain relative to the forcing input as follows:

$$ {\text{gain in dB = }}20\,{ }log_{10} \left( {\frac{{Y_{3} - Y_{4} }}{{Y_{1} - Y_{2} }}} \right) $$

(3)

where $Y_{i}$ refers to the y-coordinate of the point $i$ in Fig. 9. Specifically, points 1 and 3 are the peaks and points 2 and 4 are the troughs. This method of analysing the frequency response of a nonlinear system tends to give identical results to the classical (linear) method when the forcing amplitude is small. In the pitch rocking manoeuvre, a large amplitude is almost certainly used, and this can result in a frequency response that differ significantly from its linear counterpart.

Fig.9

Example of a nonlinear forced response

We will now examine the angle-of-attack-to-stabilator frequency responses of the aircraft trimmed in deep stall at neutral stabilator ($\delta_{{\text{s}}}$=0°). A linear model was also obtained by numerically linearising the nonlinear model at this operating point for comparison, which has the transfer function:

$$ \frac{\alpha \left( s \right)}{{\delta_{s} \left( s \right)}} = \frac{{ - 0.0044843 \left( {s + 114.9} \right) \left( {s^{2} + 0.3006s + 0.03046} \right)}}{{\left( {s^{2} + 0.3017s + 0.03056} \right) \left( {s^{2} + 0.04681s + 1.731} \right)}} \left( {\frac{{{\text{deg}}}}{{{\text{deg}}}}} \right) $$

(4)

For a very small forcing amplitude like $A$ = 0.1°, Fig. 10a shows that the linear and nonlinear frequency responses are identical, which is expected. What is more notable is that there is only one prominent peak from the short-period (fast) mode at 1.32 rad/s, whereas the contribution from the slow (phugoid) mode in the $\alpha$ response is almost negligible. This is very different from the typical frequency response at low angles-of-attack, where both the fast and slow modes are distinctively visible. The non-standard shape of the frequency response also agrees with the time simulations observed in Fig. 7, where only one lightly damped mode is visible (even though there are technically two).

Fig. 10

Linear and nonlinear frequency responses at four different forcing amplitudes. The two ‘x’ marks in d are the points at which the numerical solver failed due to the large-amplitude solutions that exceed the viable aerodynamic data region

When $A$ is increased slightly to 1° (which is still very small), Fig. 10b shows that the resonant peak now leans to the left, indicating a nonlinear softening system with an amplitude dependency. At $A$ = 8° in Fig. 10c, the leaning increases considerably, and the subharmonic components at low frequencies are now visible. This explains the time-domain responses in Fig. 7 and their Fourier analysis in Fig. 8, where increasing the amplitude led to a gradual reduction in the oscillation frequency (as well as making the additional harmonics more prominent). From the pilot’s perspective, these behaviours bring the following implications:

• Different ways of entering the deep stall will result in oscillations with different natural frequencies. This requires active monitoring from the pilot if the current recovery procedures are followed, resulting in very high workload with possibilities of unsuccessful recovery.

• Max-amplitude (stop-to-stop) stabilator movement will be intuitively used by the pilot to achieve the highest oscillation amplitude. Due to the softening behaviour, the best forcing frequency for an optimal recovery may be lower than the frequency observed at deep stall entry.

We verify the hypothesis made in the second point by examining the nonlinear frequency response at $A$=25°, which is the value for stop-to-stop stabilator movement in Fig. 10d. At such a large amplitude, there are a few intervals of $\omega$ where no stable solution exists due to various period-doubling and torus bifurcations. Time simulations at some randomly chosen frequencies below 1.32 rad/s (the linear resonant frequency) verify that the oscillation amplitude diverges to infinity in most cases, which is exactly what we need to escape the deep stall. In practice, once the angle-of-attack drops to a reasonably low value (e.g. below the 25° limit imposed by the control system, where Fig. 5 indicates the return of substantial pitch control power), the pilot can stop the harmonic forcing input, turn the flight control computer back on, and resume normal flight. Furthermore, it is not recommended to rely on linear analysis to devise an escape manoeuvre. If we force the aircraft at the linear resonant frequency of 1.32 rad/s, then the magnified view of the $A$=25° frequency response in Fig. 11a shows that the nonlinear solution at this frequency is stable, suggesting it may not be an optimal frequency for escaping this flight regime. This is verified by time simulation in Fig. 11b, where the forced responses at 1.32 rad/s (linear resonant frequency) and 1.0 rad/s (a nearby frequency with no stable solution) are compared. The latter clearly has a much larger amplitude, which successfully reduces the angle-of-attack to below 25^o in less than 15 s and exhibits exponentially growing oscillation amplitude. In practice, the pilot would stop pumping the stick and resume normal flight at low $\alpha$ by turning the flight control computer back on as soon as the angle-of-attack drops to a reasonable value. On the other hand, the 1.32 rad/s response is stable and never dropped below 37° angle-of-attack. Its steady-state oscillation troughs are still above $\alpha$=50°—well within the deep stall regime.

Fig. 11

Magnified view of the max-amplitude frequency response in Fig. 10d a and simulated responses with two different forcing frequencies b

The recovery method presented here relies on there being an unstable region in the nonlinear frequency response which can then be exploited to initiate recovery. Deep stall requires pitch instability, as reflected in the pitching moment variations with $\alpha$ in Fig. 5 for the F-16 aircraft (positive slope unstable, negative slop stable). This type of pitching moment trend is a characteristic of deep stall and always involves ranges of alpha in which the aircraft is statically unstable. Hence it can be anticipated that for any aircraft in deep stall, harmonic forcing at a large enough amplitude is likely to result in the aircraft experiencing excursions sufficiently far into the unstable region as to provoke divergence from deep stall. The nonlinear frequency response approach, derived from numerical bifurcation analysis, provides the necessary information on the range(s) of forcing frequency at which the aircraft is indeed unstable.

Referring back to the nonlinear frequency response, there is also a region of unstable solutions between 1.81 and 4.24 rad/s as seen in Fig. 10d, which is bounded by a pair of torus bifurcations. It may be tempting to use them since they are higher than the resonant frequency and therefore may promise a faster recovery. However, time simulation at 3.0 rad/s forcing in (Fig. 12) shows that the motion is not divergent but are probably bounded quasi-periodic oscillations. The amplitude also grows rather slowly comparing to the response at 1.0 rad/s, making this unstable region unsuitable for our purpose. The lesson learned here is similar to any previous work using bifurcation methods: that time simulation must supplement the analysis to ensure that the transient dynamics is satisfactory.

Fig. 12

Forced $\alpha$ response at $\omega$=3.0 rad/s

Based on the results presented in this section, it is likely that an appropriate value to select for $\omega$ will be below the linear resonant frequency due to the softening characteristic. The proposed procedure for deep stall recovery analysis is then to use nonlinear frequency analysis at stop-to-stop stabilator movements (max amplitude) to determine a range of harmonic forcing frequencies where only unstable solutions exist. This list can be further narrowed down using time simulation to determine the frequencies that diverge the aircraft quickly. When a deep stall is encountered, either the pilot or the pre-programmed flight control computer will force the pitch control device at one of these frequencies to gain momentum and bring the nose down. Unlike in [10], this method allows the manoeuvre to be done in an open-loop manner with reduced workload and results in a higher chance of recovery. The proposed low-frequency manoeuvre also minimises the chance of encountering actuator rate limiting and does not rely on quick, square wave stabilator movements as proposed in [13], which cannot be achieved physically.

5 Nonlinear dynamics near resonance

Section 4 has revealed that the dynamics near resonance is highly nonlinear. A more detailed understanding of these behaviours can uncover the nature of these divergent oscillations and quantify the robustness our proposed deep stall recovery method. In this section, the forcing frequency $\omega$ is fixed at 0.7 rad/s, which is well below the linear resonance frequency of 1.32 rad/s, while the forcing amplitude $A$ is the continuation parameter. The resulting bifurcation diagram is shown in Fig. 13. As the forcing amplitude increases, two period-2 branches are detected, covering $A$ between 10.85 and 23.14 deg in addition to 24.48 deg and above. Stable solutions are detected in both period-2 branches, but they exist over small intervals before undergoing period-doubling cascades (not shown for clarity) that result in divergent oscillations.

Fig. 13

Bifurcation diagram—continuation in forcing amplitude. Both upper and lower bounds of the oscillations are shown. $\omega$ is fixed at 0.7 rad/s. Inset shows magnified view near the maximum amplitude

The existence of stable solutions at high forcing amplitudes, especially the period-1 branch covering $A$ between 23.14 and 24.48 deg, plus the fact that all period-doubling bifurcations are supercritical, may raise doubts on the effectiveness of the pitch rocking manoeuvre. However, time simulations reveal that these stable solutions are weak attractors because unless the state trajectories are sufficiently close to these stable solutions, the aircraft still diverges. This can be demonstrated by comparing two time simulations with same forcing input but different initial conditions. Figure 14 shows the resulting oscillations at $A$=11 deg, which is predicted to be period-2 stable. When the initial condition is set to be trimmed flight at stick neutral ($\delta_{{\text{s}}}$=0°), the aircraft still diverges as shown in Fig. 14a. In fact, the stable period-2 oscillation is only observable when the initial trajectory is sufficiently close as shown in Fig. 14b. Divergent oscillation is therefore still possible despite the significantly smaller forcing amplitude (11 deg instead of the maximum 25 deg) and the presence of stable attractors, as long as the forcing frequency is near resonance. Although time simulations are required to determine whether the aircraft would diverge, continuation-based analysis can provide an indication of where divergent behaviour might be possible, i.e. when unstable solutions and bifurcations start to appear beyond $A$=10.85° in Fig. 13.

Fig. 14

Forced response at $A$=11 deg with different initial conditions: from trimmed flight a and from a point close to the stable period-2 solution b

The fact that stable attractors have little effect on deep stall recovery is further demonstrated in Fig. 15. At a forcing amplitude of 24.2 deg, bifurcation analysis predicted a stable period-1 response. However, time simulation from trim (Fig. 15a) shows that the aircraft still diverges. The predicted stable period-1 response seen in Fig. 15b can be observed by setting initial conditions close to the stable attractor.

Fig.15

Forced response at $A$=24.2 deg with different initial conditions: from trimmed flight a and from a point close to the stable period-1 solution b

6 Conclusions

In this paper, we have shown show how bifurcation theory and nonlinear frequency analysis can facilitate a systematic study on identifying possible deep stall escape manoeuvres. Despite very limited pitch control authority at high angles-of-attack, it is still possible to initiate recovery by forcing the pitch control device at one of the nonlinear resonant frequencies, which results in large-amplitude oscillation that eventually rocks the aircraft out of the previously unrecoverable deep stall. These large-amplitude resonances are reflected as asymptotically unstable solutions, and their frequencies can be identified using our method. Furthermore, this paper also provides another example of how nonlinear-based analysis can be a useful tool for flight dynamics studies.

Previous research into deep stall recovery has encountered numerous difficulties due to the nonlinear nature of flight dynamics at high angle-of-attack. Many promising procedures also require a dynamic (nonstationary) approach, which further stretches the limits of existing analysis techniques and highlights the need for a more nonlinear-based method. With future aircraft designs continuing to stretch the operating envelope, it is also crucial that the toolbox is expanded accordingly in order to correctly predict the flight dynamics at these highly nonlinear regimes.

For further studies, the transition from two to one effective resonance frequency in the frequency response should be examined. This can be done by examining the eigenvectors of equilibrium solutions in the unforced bifurcation diagram, which provides a quantifiable metric to assess the merging of the short period and phugoid peak. A preliminary analysis of the F-16 dynamics (albeit not in the deep stall region) can be found in [35].

Appendix

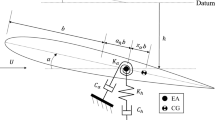
This section presents the steps to construct the 4th-order longitudinal F-16 simulation. The model contains only longitudinal aerodynamic data from reference [10] and is valid for angles-of-attack between − 20° and 90°. The use of leading edge device, flaps, and speed brake is not considered. This model and the Dynamical Systems Toolbox can be download from (https://www.researchgate.net/profile/Duc-Nguyen-38/publications). Both have been tested on MATLAB R2019a. A schematic of the simulation is shown in Fig. 16.

Fig.16

Schematic of the F-16 simulation

Aircraft parameters

$S$	Wing area	28.87 m2
$c$	Mean aerodynamic chord	3.4503 m
$m$	Mass	9,294 kg
$\rho$	Air density (at 30,000 ft)	0.45831 kg/m3
$I_{y}$	Pitch moment of inertia	75,643 kg m2
$g$	Gravitational acceleration	9.81 m/s2

Input parameters

$\delta_{s}$	Stabiliser deflection	–25° ≤ $\delta_{S}$ ≤ 25o
$T$	Thrust	8,785 N
$cg$	C.G. position	37.5 (% MAC)

Equations of motion

$\alpha$	Angle-of-attack	(rad)
$V$	Velocity	(m/s)
$q$	Pitch rate	(rad/s)
$\theta$	Pitch angle	(rad)

$$ \dot{\alpha } = \frac{1}{mV}\left[ {\frac{1}{2}\rho V^{2} S\left( {C_{Z} \cos \alpha - C_{X} \sin \alpha } \right) - T\sin \alpha + mg\cos \left( {\theta - \alpha } \right)} \right] + q $$

(5)

$$ \dot{V} = \frac{1}{m}\left[ {\frac{1}{2}\rho V^{2} S\left( {C_{Z} \sin \alpha + C_{X} \cos \alpha } \right) + T\cos \alpha - mg\sin \left( {\theta - \alpha } \right)} \right] $$

(6)

$$ \dot{q} = \frac{1}{2}\rho V^{2} Sc\frac{{C_{M} }}{{I_{y} }} $$

(7)

$$ \dot{\theta } = q $$

(8)

To plot the flight trajectory as in Fig. 4, integrate Eqs. (9–10):

$$ \dot{x} = V\cos \left( {\theta - \alpha } \right) $$

(9)

$$ \dot{z} = - V\sin \left( {\theta - \alpha } \right) $$

(10)

Note that $\theta - \alpha$ equals the flight path angle $\gamma$.

Lookup tables

$$ C_{X} = C_{{X_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right) + \frac{cq}{{2V}}C_{{X_{q} }} \left( \alpha \right) $$

(11)

$$ C_{Z} = C_{{Z_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right) + \frac{cq}{{2V}}C_{{Z_{q} }} \left( \alpha \right) $$

(12)

$$ C_{M} = C_{{M_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right) + \frac{cq}{{2V}}C_{{M_{q} }} \left( \alpha \right) + \Delta C_{{M_{\alpha } }} \left( \alpha \right) + \left( {0.35 - \frac{cg}{{100}}} \right)C_{Z} $$

(13)

The result presented in this paper used MATLAB’s spline interpolation/extrapolation for 2D tables and ‘pchip’ interpolation for 1D tables.

$C_{{X_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right)$		$\delta_{s}$(deg)
		− 25	− 10	0	10	25
$\alpha$(deg)	− 20	− 0.1868	− 0.1223	− 0.0933	− 0.0884	− 0.1141
	− 15	− 0.1875	− 0.1188	− 0.0978	− 0.101	− 0.145
	− 10	− 0.1787	− 0.1147	− 0.0982	− 0.1092	− 0.1633
	− 5	− 0.1432	− 0.0893	− 0.0784	− 0.0902	− 0.1337
	0	− 0.1132	− 0.0617	− 0.0489	− 0.0606	− 0.1075
	5	− 0.0693	− 0.0172	− 0.0066	− 0.02	− 0.0785
	10	− 0.012	0.0399	0.049	0.0313	− 0.0336
	15	0.0537	0.1027	0.1072	0.0829	0.0212
	20	0.0951	0.1322	0.1283	0.0971	0.0187
	25	0.1111	0.1407	0.13	0.0949	0.0198
	30	0.1435	0.1651	0.1536	0.1104	0.0381
	35	0.1663	0.1795	0.1605	0.1201	0.0479
	40	0.1739	0.1798	0.1552	0.1127	0.0418
	45	0.1659	0.1671	0.1382	0.0996	0.0363
	50	0.1693	0.1544	0.1281	0.1071	0.0472
	55	0.1804	0.1488	0.12	0.103	0.0484
	60	0.1718	0.1383	0.1147	0.0914	0.046
	70	0.1695	0.1328	0.1025	0.119	0.0641
	80	0.1598	0.1211	0.0821	0.0519	− 0.0173
	90	0.166	0.1247	0.0864	0.0504	− 0.0173

$C_{{Z_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right)$		$\delta_{s}$(deg)
		− 25	− 10	0	10	25
$\alpha$(deg)	− 20	1.315	1.228	1.116	1.039	0.71
	− 15	1.171	1.059	0.959	0.849	0.476
	− 10	0.925	0.815	0.692	0.596	0.205
	− 5	0.469	0.356	0.287	0.205	0.125
	0	0.155	0.064	− 0.025	− 0.114	− 0.228
	5	− 0.189	− 0.287	− 0.367	− 0.49	− 0.578
	10	− 0.53	− 0.65	− 0.75	− 0.849	− 0.946
	15	− 0.856	− 0.98	− 1.112	− 1.177	− 1.253
	20	− 1.169	− 1.306	− 1.418	− 1.442	− 1.554
	25	− 1.446	− 1.594	− 1.658	− 1.789	− 1.814
	30	− 1.717	− 1.863	− 2.008	− 2.082	− 2.108
	35	− 1.909	− 2.09	− 2.2	− 2.308	− 2.248
	40	− 2.037	− 2.216	− 2.328	− 2.411	− 2.337
	45	− 1.985	− 2.263	− 2.311	− 2.306	− 2.327
	50	− 1.959	− 2.097	− 2.326	− 2.261	− 2.261
	55	− 2.01	− 2.088	− 2.252	− 2.231	− 2.231
	60	− 1.916	− 2.051	− 2.208	− 2.185	− 2.174
	70	− 1.957	− 2.027	− 2.134	− 2.268	− 2.259
	80	− 1.816	− 1.916	− 2.004	− 1.94	− 1.899
	90	− 1.978	− 1.998	− 2.14	− 2.057	− 2.069

$C_{{M_{{\alpha ,\delta_{s} }} }} \left( {\alpha ,\delta_{s} } \right)$		$\delta_{s}$(deg)
		− 25	− 10	0	10	25
α(deg)	− 20	0.175	0.0864	0.0127	− 0.0835	− 0.2093
	− 15	0.1584	0.0328	− 0.0755	− 0.1719	− 0.3079
	− 10	0.159	0.0041	− 0.1025	− 0.2153	− 0.3391
	− 5	0.1216	0.0076	− 0.0774	− 0.1888	− 0.274
	0	0.1409	0.043	− 0.0598	− 0.161	− 0.2527
	5	0.158	0.0501	− 0.0498	− 0.1606	− 0.2562
	10	0.1845	0.0553	− 0.0437	− 0.1548	− 0.2554
	15	0.2087	0.0706	− 0.0407	− 0.1452	− 0.216
	20	0.2152	0.0674	− 0.0342	− 0.1264	− 0.2165
	25	0.1978	0.0492	− 0.0507	− 0.153	− 0.2325
	30	0.2022	0.0528	− 0.0459	− 0.144	− 0.174
	35	0.1814	0.0278	− 0.0605	− 0.1411	− 0.1401
	40	0.1478	− 0.0094	− 0.0835	− 0.145	− 0.132
	45	0.0922	− 0.0411	− 0.0923	− 0.1411	− 0.1113
	50	0.0745	− 0.0129	− 0.0826	− 0.1008	− 0.1234
	55	0.0713	0.0202	− 0.0738	− 0.0679	− 0.0929
	60	− 0.054	− 0.0708	− 0.1414	− 0.1556	− 0.1584
	70	− 0.2244	− 0.3137	− 0.3216	− 0.1983	− 0.2303
	80	− 0.3389	− 0.4236	− 0.4678	− 0.4721	− 0.4716
	90	− 0.4723	− 0.5718	− 0.6184	− 0.6083	− 0.5886

		$C_{{X_{q} }} \left( \alpha \right)$	$C_{{Z_{q} }} \left( \alpha \right)$	$C_{{M_{q} }} \left( \alpha \right)$	${\Delta }C_{{M_{\alpha } }} \left( \alpha \right)$
$\alpha$(deg)	− 20	0.953	− 23.9	− 6.84	0.019
	− 15	0.953	− 23.9	− 6.84	0.019
	− 10	0.953	− 23.9	− 6.84	0.019
	− 5	1.55	− 29.5	− 3.42	0.019
	0	1.9	− 29.5	− 5.48	0.019
	5	2.46	− 30.5	− 5.45	0.019
	10	2.92	− 31.3	− 6.02	0.02
	15	3.3	− 30.1	− 6.7	0.04
	20	2.76	− 27.7	− 5.69	0.04
	25	2.05	− 28.2	− 6	0.05
	30	1.5	− 29	− 6.2	0.06
	35	1.49	− 29.8	− 6.4	0.06
	40	1.83	− 38.3	− 6.6	0.06
	45	1.21	− 35.3	− 6	0.06
	50	1.33	− 32.3	− 5.5	0.06
	55	1.61	− 27.3	− 5	0.06
	60	0.91	− 25.2	− 4.5	0.06
	70	3.43	− 27.3	− 3.5	0.06
	80	0.617	− 9.35	− 5.6	0.06
	90	0.273	− 2.16	− 4.04	0.06

Linear analysis

The following state-space model was obtained from the trimmed aircraft in deep stall at $\delta_{{\text{s}}}$ = 0°, $T$ = 8785 N, $cg$=37.5,$q$=0 deg/s, $\alpha$=58.5 deg, $V$=79.8 m/s, and $\theta$=8.5 deg. Note that $q$, $\alpha$, and $\theta$ have units rad/s or rad in the state-space matrices.

$$ {\varvec{x}} = \left[ {q,\alpha ,V,\theta } \right]^{T} {\varvec{u}} = \delta_{{\text{s}}} $$

$$ \begin{gathered} {\varvec{A}} = \left[ {\begin{array}{*{20}c} { - 0.16093} & { - 1.77576} & {4.40366e - 07} & 0 \\ {0.98316} & {0.01311} & { - 0.00173} & {0.09415} \\ { - 2.00203} & {1.25473} & { - 0.20067} & { - 6.30705} \\ 1 & 0 & 0 & 0 \\ \end{array} } \right]\;{\varvec{B}} = \left[ {\begin{array}{*{20}c} { - 0.00920} \\ { - 7.82661e - 05} \\ { - 0.03019} \\ 0 \\ \end{array} } \right] \hfill \\ {\varvec{C}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\,{\varvec{D}} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] \hfill \\ \end{gathered} $$