Hard versus soft impact modeling of vibro-impact systems with a moving base

Abstract

Soft and hard impact models applied to modeling of vibro-impact systems with a moving base are discussed. The conditions under which two collision models are equivalent in terms of equal energy dissipation are derived. These conditions differ from those presented in the literature. It is shown that in the case of a stiff, harmonically moving base with a low rate of energy dissipation, both methods yield the same results, but an application of the soft impact model to either the base with low stiffness or even the stiff base with a high rate of energy dissipation leads to different results from the ones for the hard impact model.

1 Introduction

Mechanical systems with elements impacting on one another during operation are an important field of investigations in dynamics. These systems are represented by pneumatic hammers, impact print hammers [1], and heat exchangers [2, 3], in which impact is a desirable effect, but also by gearboxes [4], where it is disadvantageous or even destructive. Characteristics of the impacting motion and its accompanying dynamical phenomena originally investigated by Goldsmith [5], Feigin [6], Peterka [7] and Fillippov [8] have been thoroughly studied ever since by numerous researchers.

A crucial difficulty in modeling of vibro-impact systems lies in a selection of the appropriate impact model. Within the classical approach to the collision process, referred to as Newton’s or hard collision model, an infinitely short contact of non-deformable bodies at impact and a constant value of the coefficient of restitution that defines the energy dissipation are assumed. As might be expected, assumptions of a hard impact model can be met only approximately and in certain situations. For example, they are reasonably valid for an analysis of moderate velocity collisions of sufficiently stiff bodies, whose shapes (e.g., two spheres or a sphere and a large rigid mass) ensure slight deformations, short impact durations and conversion of negligible fractions of energy dissipated during impacts into vibrations of the impacting bodies [5]. When the finite nonzero contact time and the deformation of colliding bodies are considered, it leads to a soft impact model, which describes more accurately the process of collision. This model allows an application of different types of elastic-damping constructions to simulate impacts. An introduction of various impact rheological elements has made it possible to describe a wider range of physical processes taking place in impact systems [9,10,11,12]. For a comprehensive survey of the current methods of vibro-impact systems modeling, see, e.g., the monograph by Ibrahim [13].

A harmonically forced linear oscillator with an amplitude constraint is considered to be the simplest model to investigate impacting systems. It has been widely explored as regards both rigid (e.g., [14,15,16,17,18]) and soft constraints (e.g., [19,20,21,22,23,24,25,26,27]), with particular attention paid to stability of periodic solutions, bifurcations and singularities in vibro-impact dynamics. Intensive tests of impact systems have led to the development of a set of tools to identify and assess qualitatively and quantitatively the dynamic phenomena occurring in piecewise smooth systems (see, e.g., [28,29,30,31,32,33,34]).

The applicability of soft and hard impact models in modeling of vibro-impact systems with a moving base is discussed. The conditions under which both methods are equivalent in terms of equal energy dissipation are described. It should be stressed that the conditions presented here differ from those obtained in the same context in [35]. In fact, they are body-base analogues of the conditions for two finite mass bodies presented in [36]. It is shown that in the case of a stiff moving base with a low rate of energy dissipation, both methods of impact modeling yield the same results, but for a base with low stiffness as well as for a stiff base with a high rate of energy dissipation, an application of hard and soft impact models leads to different results.

The paper is organized as follows. In Sect. 2, we investigate the dynamical behavior of the body (material point) which collides orthogonally against a vertical base when hard and soft impacts are considered, and we derive the conditions which allow the same energy dissipation in both models. An influence of impact modeling on the dynamics of a one degree-of-freedom system with a moving base, whose mathematical model is introduced in Sect. 3 and which, in addition to being interesting on its own, represents an impacting cantilever beam system, is discussed in Sect. 4. Finally, the results obtained are summarized in Sect. 5.

2 Impact models

Collision of a rigid body of the mass $m$ with a base can be modeled in two qualitatively different ways. The body is assumed to move along the horizontal straight line toward the vertical base, with a constant velocity v₀. If both the colliding body and the base are stiff, then on the basis of the definition of the coefficient of restitution at inelastic impact, the velocity of the mass $m$ before collision v₀ and its velocity after collision v₁ satisfies the following relation:

$$ v_{1} = - rv_{0} , $$

(1)

where r is the restitution coefficient. Relation (1) is known as the Newton’s law of impacts.

Within the second approach to impact modeling, the mass m is assumed to collide against the base modeled as a light fender supported by a light spring with the stiffness coefficient k_s and a light viscous damper with the damping coefficient c_s, which is illustrated in Fig. 1. Here, the time of collision is positive and the base can be penetrated by the colliding body. As a result, different dynamical behaviors with hard and soft impacts of vibro-impact systems can be observed.

Fig. 1

Soft model of the colliding body with the base modeled as a light barrier

Our objective now is to estimate a relation between the coefficients k_s, c_s and r, which enables the same energy dissipation. Let u(t) denote the displacement of the body, measured from the reference point on the line, along which the body moves and let $\dot{u}(t)$ stand for the corresponding velocity. Hereafter, the dot denotes differentiation with respect to time.

Without loss of generality, we will assume that the body collides with the base at $t_{0} = 0$ with $u(t_{0} ) = 0$ and $\dot{u}(t_{0} )$ = $v_{0} ,$ where $v_{0} < 0$. The dynamics of the body during collision is governed by the following equation:

$$ m\ddot{u} + c_{{\text{s}}} \dot{u} + k_{{\text{s}}} u = 0 $$

(2)

with the initial conditions:

$$ u(0) = 0,\dot{u}(0) = v_{0} . $$

(3)

The general solution to Eq. (2) can be written in the form:

$$ u(t) = e^{{ - \beta _{s} t}} A\sin (\lambda _{s} t + \psi ), $$

(4)

where $\lambda _{s} = \sqrt {\alpha _{s} ^{2} - \beta _{s} ^{2} }$, in which $\alpha _{s} = \sqrt {k_{s} /m}$ and $\beta _{s} = c_{s} /(2m)$, is the frequency of free vibrations of the damped system, whereas the amplitude A and the phase shifting ψ are constants depending on the initial conditions. The velocity of the oscillator can be written as:

$$ \dot{u}(t) = - \beta _{s} e^{{ - \beta _{s} t}} A\sin (\lambda _{s} t + \psi ) + \lambda _{s} e^{{ - \beta _{s} t}} A\cos (\lambda _{s} t + \psi ). $$

(5)

From Eqs. (3), (4) and (5), it follows that:

$$ u(t) = e^{{ - \beta _{s} t}} \frac{{v_{0} }}{{\lambda _{s} }}\sin (\lambda _{s} t) $$

(6)

and

$$ \dot{u}(t) = - \beta _{s} e^{{ - \beta _{s} t}} \frac{{v_{0} }}{{\lambda _{s} }}\sin (\lambda _{s} t) + v_{0} e^{{ - \beta _{s} t}} \cos (\lambda _{s} t). $$

(7)

After the initiation of collision at $t_{0} = 0$, the body will be in contact with the base and they will separate at the first instant $t_{1} > 0$, when the displacement $u(t_{1} )$ = 0 and the velocity $\dot{u}(t_{1} )$ > 0. In view of Eqs. (6) and (7), these conditions are satisfied for

$$ t_{1} = \pi /\lambda _{s} . $$

(8)

and the velocity of the body at the instant $t_{1}$ equals

$$ v_{1} = \dot{u}(t_{1} ) = - v_{0} e^{{ - \beta _{s} \frac{\pi }{{\lambda _{s} }}}} > 0. $$

(9)

as, by assumption, $v_{0} < 0.$ Since the kinetic energy of the body at the beginning of impact is the same for both types of impact models, in order to have the same energy losses, it suffices to equate the kinetic energies at the end of impact, or equivalently, to equate the velocities at the end of impact. Combining (1) and (9), it can be concluded that:

$$ r = e^{{ - \frac{{\beta _{s} }}{{\lambda _{s} }}\pi }} , $$

and, consequently

$$ r = e^{{ - \frac{{\xi _{s} }}{{\sqrt {1 - \xi _{s} ^{2} } }}\pi }} , $$

(10)

in which

$$ \xi _{s} = \frac{{c_{s} }}{{2\sqrt {k_{s} m} }} $$

(11)

is the dimensionless damping, related to the critical one. As shown in Eq. (10), the energy dissipated during the soft collision depends monotonically on the value of the parameter ξ_s, i.e., with an increase in ξ_s, the rate of energy dissipation becomes lower. On the other hand, it follows from Eq. (11) that the amount of energy dissipated for two various bases with the coefficients k_s,1, c_s,1 and the coefficients k_s,2, c_s,2, correspondingly, is equal, provided the relation (c_s,1/c_s,2)² = k_s,1/k_s,2 is satisfied.

From Eqs. (10) and (11), finally the desired relation is obtained:

$$ c_{s} = 2\xi _{s} \sqrt {k_{s} m} $$

(12)

with

$$ \xi _{s} = \frac{{ - \ln r}}{{\sqrt {\pi ^{2} + (\ln r)^{2} } }}. $$

(13)

Hence, for any given value of the restitution coefficient $r$, Eqs. (12) and (13) allow one to determine the base parameters k_s and c_s, which makes the two models equivalent in terms of energy losses. Note that the obtained relation (13) between $\xi _{s}$ and r for a finite mass body hitting the base is identical to the relation between $\xi _{s}$ and r for two finite mass bodies hitting each other (see Eq. 2 in [36]). Clearly, a decrease in the restitution coefficient $r$ results in an increase in the damping coefficient c_s. It should be also noted that relation (10) is different from the one presented in [35], i.e.:

$$ r^{\prime} = \sqrt {1 - (1 + \xi ^{2} )(1 - e^{{ - 2\pi \xi }} )} , $$

(14)

where $\xi ^{2} = \xi _{s} /(1 - \xi _{s}^{2} )$, which is only valid for $\xi _{s}$ not greater than approximately 0.33. The values of r and $r^{\prime}$ versus $\xi _{s}$ are shown in Fig. 2. Notice that the graph of r is situated above the graph of $r^{\prime}$. For low values of $\xi _{s}$, the graphs are close to each other, but for larger values of ξ_s, they differ significantly.

Fig. 2

Relations between the parameters r (line 1) and $r^{\prime}$ (line 2) versus $\xi _{s}$

In the situation under consideration, where neither the body nor the base is subjected to external forces, equivalent impact models lead to the same velocities after impact and the only difference is the soft bumper response time lag, equal to the duration of contact $\tau = \sqrt {m(\pi ^{2} + (\ln r)^{2} )/k_{s} }$. In the next sections, it will be examined what effect will be exerted on the behavior of both systems by an application of an additional elastic-damping element to the body and external forcing to the base. It should be emphasized that in the case under consideration, it is not possible to determine analytically the counterpart of the relation given by Eqs. (12)-(13). The main obstacle to achieve such a relation lies in an inability to derive closed-form expressions for the moments at which collisions occur.

3 Model of the system

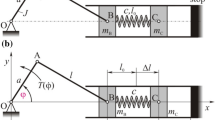
A linear oscillator of mass m, coefficient of viscous damping c and spring stiffness coefficient k (Fig. 3a) is subject to investigation. External forcing is applied to the oscillator, i.e., the spring upper end moves with a harmonic motion $a\sin (\eta t)$ of given amplitude a and frequency $\eta$. During the motion, the oscillator bottom surface can collide against a moving base. The base and the upper end of the spring move in the same way. When the system reaches the static equilibrium position, the distance between its impacting surface and the base is equal to d. The coordinate x describes the motion of the oscillator around its static equilibrium position.

Fig. 3

Impacting oscillator with damping and kinematic external excitation: hard contact model (a), soft contact model (b)

The equation of the impactless motion of the above-described system is as follows:

$$ m\ddot{x} + c\dot{x} + kx = ka\sin (\eta t). $$

(15)

For some system parameters, there is a possibility of contact of the mass with the stops, i.e., a deflection of the mass of -d (Fig. 3a). In the rest of this paper, an influence of impact modeling on the system behavior is discussed.

In the hard impact case, when the contact of non-deformable bodies is assumed to be negligibly short and the energy dissipation during this impact is described by a constant coefficient of restitution, the oscillator behavior between successive impacts is governed by Eq. (15), whereas at the instants of impact, the following Newton transition conditions are used:

$$ v_{r}^{ + } = - rv_{r}^{ - } , $$

(16)

in which r is the coefficient of restitution, $v_{r}^{ - }$ denotes the relative velocity of the oscillator before impact and $v_{r}^{ + }$ stands for the relative velocity after impact, where the relative velocity $v_{r}$ is given as $v_{r} (t) = \dot{x}(t) - a\eta \cos (\eta t)$.

To consider the impact duration and deformation of the colliding bodies, impact forces have to be modeled properly. The linear model presented in Sect. 2 (cf. [35]) is a possible solution. The system with a soft impact model (equivalent to a hard impact model as far as identical energy dissipation is concerned), which corresponds to the system described by Eqs. (15) and (16), is as follows:

$$ m\ddot{x} + c\dot{x} + kx + F_{d} = ka\sin (\eta t), $$

(17)

where $F_{{\text{d}}}$ stands for the collision force (Fig. 3b), i.e.:

$$ \begin{array}{*{20}l} {F_{d} = 0} \hfill & {x - a\sin (\eta t) - d \ge 0,} \hfill \\ {F_{d} = k_{s} \left( {x - a\sin (\eta t) - d} \right) + c_{s} \left( {\dot{x} - a \eta \cos (\eta t)} \right)} \hfill & {x - a\sin (\eta t) - d < 0,} \hfill \\ \end{array} $$

(18)

in which k_s denotes the coefficient of stiffness of the constraint, c_s is the coefficient of damping of the constraint, related to the coefficient of restitution r by equating the energy losses during impact, defined by the relationship given by Eqs. (12) and (13), whereas the remaining quantities are expressed as in formula (15).

The equations of motion (15) and (17), (18) were integrated within the Runge–Kutta–Gill method, whereas a method of successive numerical approximations was employed to define the moments of impacts. The dynamic behavior of the system was determined by time series, phase trajectories, an average number of impacts per excitation period, average energy dissipation during impacts per excitation period and bifurcation diagrams of relative displacements, relative velocities at impact moments and spectra of Lyapunov exponents, obtained during the integration procedure. The spectra of Lyapunov exponents were determined according to Müller’s method [31] for a piecewise smooth time-varying system, i.e., a system which evolves according to the equations:

$$ {t_{i - 1}} < t < {t_i}:\quad {\mathbf{\dot x}} = {{\mathbf{f}}_i}({\mathbf{x}},t),\quad {\mathbf{x}}({t_{i - 1}}) = {{\mathbf{x}}^{(i - 1) + }}, $$

(19)

$$t = {t_i}:\quad {\text{0}} = {\mathbf{h}}{\text{(}}{\mathbf{x}}({t_i}), {t_i}{\text{)}} = {\text{0,}}\quad {{\mathbf{x}}^{i + }} = {\mathbf{g}}({{\mathbf{x}}^{i - }},{t_i}), $$

(20)

$$ {t_i} < t < {t_{i + 1}}:\quad {\mathbf{\dot x}} = {{\mathbf{f}}_{i + 1}}({\mathbf{x}},t),\quad {\mathbf{x}}{\text{(}}{t_i}{\text{)}} = {{\mathbf{x}}^{i + }}, $$

(21)

where $i = {\text{1,2,}} \ldots {\text{,}}{\mathbf{x}}^{{0 + }} = {\mathbf{x}}_{0} {\text{,}}{\mathbf{f}}_{i} ,\user2{g},\user2{h}$, are continuously differentiable, ${\mathbf{x}}^{{i - }} = \lim _{{t \uparrow t_{i} }} {\mathbf{x}}(t)$ and ${\mathbf{x}}^{{i + }} = \lim _{{t \downarrow t_{i} }} {\mathbf{x}}(t)$, combined with the classical method for smooth systems proposed by Benettin et al. [37]). Müller [31] shows that the transition conditions of the linearized equations of motion corresponding to (19) and (21) at the instant of the ith singularity take the following form:

$$ \delta {\mathbf{x}}^{{i + }} = \frac{{\partial {\mathbf{g}}}}{{\partial {\mathbf{x}}}}({\mathbf{x}}^{{i - }} ,t_{i} ) \delta {\mathbf{x}}^{{i - }} + \left( {\frac{{\partial {\mathbf{g}}}}{{\partial {\mathbf{x}}}}({\mathbf{x}}^{{i - }} ,t_{i} ) {\mathbf{f}}_{i} \left( {{\mathbf{x}}^{{i - }} ,t_{i} } \right) - {\mathbf{f}}_{{i + 1}} \left( {{\mathbf{x}}^{{i + }} ,t_{i} } \right) + \frac{{\partial {\mathbf{g}}}}{{\partial t}}({\mathbf{x}}^{{i - }} ,t_{i} )} \right) \delta t_{i} {\text{ ,}} $$

(22)

where $\delta {\mathbf{x}}^{{i - }}$ and $\delta {\mathbf{x}}^{{i + }}$, respectively, denote the value of the perturbation immediately before and immediately after the moment of the ith singularity, and

$$ \delta t_{i} = - \frac{{\frac{{\partial {\mathbf{h}}}}{{\partial {\mathbf{x}}}}({\mathbf{x}}^{{i - }} ,t_{i} )\delta {\mathbf{x}}^{{i - }} }}{{\frac{{\partial {\mathbf{h}}}}{{\partial {\mathbf{x}}}}({\mathbf{x}}^{{i - }} ,t_{i} ) {\mathbf{f}}_{i} \left( {{\mathbf{x}}^{{i - }} } \right) + \frac{{\partial {\mathbf{h}}}}{{\partial t}}({\mathbf{x}}^{{i - }} ,t_{i} )}}. $$

In the case of Newton’s contact model, the functions ${\mathbf{f}}_{{2i - 1}}$ and ${\mathbf{f}}_{{2i}}$ in (19) and (21) are equal to:

$$ {\mathbf{f}}(x_{1} ,x_{2} ) = \left( {x_{1} ,\,\frac{{ka}}{m}\sin ({{\eta }}t) - \frac{c}{m}x_{2} - \frac{k}{m}x_{1} } \right), $$

and the Jacobi matrices of the transition functions ${\mathbf{h}}({\mathbf{x}}) = x_{1} - a\sin (\eta t) - d$ and ${\mathbf{g}}({\mathbf{x}}) = \left[ {x_{1} , - rx_{2} } \right]$ at the instant immediately before the ith singularity are as follows:

$$ \frac{{\partial {\mathbf{h}}}}{{\partial {\mathbf{x}}}} ({\mathbf{x}}^{i-}, t) = [1, 0],\,\,\frac{{\partial {\mathbf{h}}}}{{\partial {\mathbf{x}}}}({\mathbf{x}}^{i-}, t) = \left [\begin{array}{cc}1 & 0 \\ 0 & -r \end{array} \right].$$

(23)

In the case of the soft contact model (18), we have:

$$ {\mathbf{f}}_{{2i - 1}} (x_{1} ,x_{2} ) = \left( {x_{1} , \frac{{ka}}{m}\sin (\eta t) - \frac{c}{m}x_{2} - \frac{k}{m}x_{1} } \right), $$

$$ {\mathbf{f}}_{{2i}} (x_{1} ,x_{2} ) = \left( {x_{1} , \frac{{ka}}{m}\sin (\eta t) - \frac{c}{m}x_{2} - \frac{k}{m}x_{1} - \frac{{k_{s} }}{m}\left( {x_{1} - a\sin (\eta t) - d} \right) - \frac{{c_{s} }}{m}\left( {x_{2} + a\eta \cos (\eta t)} \right)} \right), $$

and the Jacobi matrices of the transition functions ${\mathbf{h}}({\mathbf{x}}) = x_{1} - a\sin (\eta t) - d$ and ${\mathbf{g}}({\mathbf{x}}) = \left[ {x_{1} ,x_{2} } \right]$ are given by (23) with − 1 written instead of r, whereas the values of the perturbations immediately after and immediately before the instant of singularity are related as in (22). The basic criterion used to distinguish between various kinds of periodic motion was the quantity z = p/n, where p denotes the number of impacts in the motion period and n stands for the number of the excitation force periods T in the motion period, i.e., $T = 2\pi /\eta$.

4 Dynamic behavior of hard vs soft impact models

The numerical investigations dealt with a comparison of the dynamic behavior of the harmonically excited system with a hard impact model with selected values of the restitution coefficient to the dynamic behaviors of the corresponding systems with equivalent (in terms of equal energy dissipation) soft impact models. The values of the coefficients of stiffness and damping of the constraint were chosen according to Eqs. (12) and (13).

4.1 Undamped hard vs soft impacts

The first model investigated was a hard impact model with the restitution coefficient r = 1. The distance d = 0.0 was assumed, and the following typical system parameters were chosen: m = 1, k = 1 and c = 0.23, where the value of the damping coefficient corresponds to the value of the damping logarithmic decrement Δ = ln(2). The values of all physical quantities appearing in the paper are given in the SI base units.

Diagrams presenting the above-described model are to found in Fig. 4a–c. Vibrations were excited with the harmonic force $a\sin (\eta t)$, where it was assumed that a = 0.0025 and the circumferential frequency was in the range from η = 2.0 to η = 10.0. The graduation on the vertical axis in Fig. 4a corresponds to values of the relative displacement $x_{r} = x_{1} - a\sin (\eta t)$ of the mass at the time instants defined by the equation sin(ηt) = 0.0, whereas the graduations on both sides of the vertical axis in Fig. 4b depict values of both Lyapunov exponents λ₁ and λ₂ (thin lines) and an average value of changes in kinetic energy of the body during impacts in the excitation period a_e (thick line), and the graduations on the vertical axes of Fig. 4c – a value of an average number of impacts in the excitation period a_i (the left axis, thin lines) and values of the relative velocity v_r of the mass at moments of impact (the right axis, points). A dependence between the nature of the system motion and the excitation force frequency values is plotted. Regions of period -1, -2, -3, 4 and -5 motions can be localized on these plots. As regards the remaining values of η, non-periodic vibrations can be observed.

Fig. 4

Bifurcation diagrams for the system with the hard contact model with r = 1; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

The corresponding diagrams calculated for four undamped soft impact models with the base stiffness coefficient k_s equal to 200,000, 2000, 500 and 100 are depicted in Figs. 5, 6, 7 and 8, correspondingly. The value of the mass m, the coefficients k and c, the way vibrations were excited and the parameter d was identical as in the hard impact model.

Fig. 5

Bifurcation diagrams for the system with the soft contact model with r = 1, k_s = 200,000; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 6

Bifurcation diagrams for the system with the soft contact model with r = 1, k_s = 2000; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 7

Bifurcation diagrams for the system with the soft contact model with r = 1, k_s = 500; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 8

Bifurcation diagrams for the system with the soft contact model with r = 1, k_s = 100; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Comparing the graphs in Fig. 4 plotted for the hard impact model to the corresponding graphs in Fig. 5 for the soft impact model with k_s = 200,000, we can observe not only their qualitative but also quantitative agreement. For identical values of the excitation force, this agreement is exemplified by an appearance of chaotic and periodic solutions with almost the same values of the respective Lyapunov exponents, as well as a very good conformity of the values of the corresponding relative displacements x_r, average numbers of impacts a_i, relative velocities v_r at the moments of impact and average changes in kinetic energy of the body during impacts a_e, which could be expected for models with considerable stiffness of the base. For example, for η = 7.1, the Lyapunov exponents of a chaotic solution to the system with soft-type collisions take the values λ₁ = 0.279972 and λ₂ = − 0.509972, whereas the Lyapunov exponents of the corresponding chaotic solution to the system with Newton-type collisions are equal to λ₁ = 0.272637 and λ₂ = − 0.502637. Thus, within chaotic zones, the corresponding rates of divergence of adjacent trajectories are almost the same, irrespective of the impact model assumed. Further information on the nature of these similarities is provided in Figs. 9 and 10, which show phase portraits for two selected values of excitation frequency. Figure 9a, b presents plots of the period-2 motion (z = 1/2) of the hard impact model (λ₁ = − 0.114979, λ₂ = − 0.115021) and the soft impact model (λ₁ = − 0.112269, λ₂ = − 0.117731) for η = 4, while Fig. 10a, b—plots of the period-4 motion (z = 1/4) of hard (λ₁ = − 0.112269, λ₂ = − 0.117731) and soft (λ₁ = − 0.111880, λ₂ = − 0.118120) impact models for η = 8. They confirm a very good conformity of the corresponding periodic phase trajectories for the hard impact model and the soft impact model with a stiff base.

Fig. 9

Phase trajectories of period-2 motion solutions (z = 1/2) for η = 4, r = 1; hard contact model (a), soft contact model for k_s = 200,000 (b)

Fig. 10

Phase trajectories of period-4 motion solutions (z = 1/4) for η = 8, r = 1; hard contact model (a), soft contact model for k_s = 200,000 (b)

While analyzing the diagrams with a decreasing value of the coefficient k_s, some minor differences between the plots for the hard impact model and the plots for the soft impact models, equivalent in terms of energy dissipation, were observed no sooner than for the system of k_s = 2000. A comparison of the bifurcation diagrams in Figs. 4 and 6 still shows a good conformity of both the ranges of periodic and non-periodic motion, relative displacements and values of both Lyapunov exponents. A decrease in the base stiffness results in inconsiderable alternations in the ranges of periodic motion, a slightly narrower range of the period-4 motion and lower average numbers of impacts a_i in chaos zones, as well as an inconsiderable decrease in values of v_r and a_e, only. Some information on the nature of these differences is provided in Fig. 11a, b presenting phase trajectories of the period-2 motion (z = 1/2) and the period-4 motion (z = 1/4) of the soft impact model calculated for η = 4 and η = 8, respectively (cf. Figs. 9a and 10a).

Fig. 11

Phase trajectories for the soft contact model with r = 1, k_s = 2000; period-2 motion solutions for η = 4 (a), period-4 motion solutions for η = 8 (b)

A comparison of the bifurcation diagrams for the hard impact model and the soft impact model with k_s = 500 (Figs. 4 and 7) reveals significant differences in the magnitude and regularity of ranges of periodic behaviors—the ranges of the period-3 and period-4 motion are considerably wider for the soft impact model, as well as the values of Lyapunov exponents in the regions of irregular behaviors—they are distinctly less extensive for the soft impact model. The values of the coefficients v_r, a_i and a_e in chaos zones are for this model significantly lower than for the hard impact model.

A further decrease in k_s leads to a sharper increase in the above-mentioned differences—an occurrence of wider ranges of regular behaviors in regions of chaotic motion, which become narrower (cf. Figs. 4a, b and 8a, b calculated for k_s = 100) and are accompanied by flatter and flatter plots of the coefficients a_i, a_e and v_r (cf. Figs. 4b, c and 8b, c). The described divergences result from the external forces, namely the excitation force and the elastic-damping force, acting on the colliding body during the nonzero contact time.

4.2 Influence of the impact energy dissipation

Systems with a decreasing value of the restitution coefficient were subject to further investigation. During the analysis of the diagrams representing this tendency of the restitution coefficient, while maintaining unaltered values of the remaining parameters, some differences between the plots for the hard impact model and the plots for the soft impact model, equivalent in terms of energy dissipation, with the base stiffness coefficient k_s = 200,000, were noticed for the system with r = 0.8—see Figs. 12 and 13. A comparison of the diagrams in Figs. 12 and 13 shows still a good coexistence of both the ranges of periodic and non-periodic motion, as well as a good conformity of the values of the corresponding values of Lyapunov exponents and the values of the characteristics x_r, v_r, and a_e. The main difference lies in noticeable larger average numbers of impacts a_i within chaotic zones for the hard impact model. Although a decrease in the base stiffness coefficient (from the value of k_s = 200,000 to k_s = 2000, k_s = 500 and k_s = 100) leads to apparently more significant discrepancies in values of all the corresponding characteristics, it was followed by a very similar effect on soft impact system behaviors as the one discussed for the case of undamped impact models. Due to the fact that the general structure of the corresponding bifurcation diagrams calculated for r = 0.8 is identical as in the case when r = 1.0 and a high similarity of the evolution of behaviors observed for r = 1.0 and k_s = 2000, k_s = 500 and k_s = 100, an inclusion of the drawings illustrating these changes for r = 0.8 and k_s = 2000, k_s = 500 and k_s = 100 was abandoned.

Fig. 12

Bifurcation diagrams for the system with the hard contact model with r = 0.8; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 13

Bifurcation diagrams for the system with the soft contact model with r = 0.8, k_s = 200,000; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Next, a hard impact model with the restitution coefficient r = 0.6 and its corresponding soft impact models with k_s = 200,000, k_s = 2000, k_s = 500 and k_s = 100 were investigated. The values of the stiffness and damping coefficients k and c, the way vibrations were excited, and the parameter d was identical as in the models with r = 0.8 and r = 1.0.

First of all, let us draw attention to considerable differences between the currently investigated hard impact model (Fig. 14) and the soft impact model even for the value of the base stiffness coefficient k_s = 200,000 (Fig. 15) when compared to the hard impact models and their corresponding soft impact models for the restitution coefficient r equal to 1.0 (Figs. 4 and 5) and 0.8 (Figs. 12 and 13). In particular, let us notice that, despite apparently similar shapes of the bifurcation diagrams of the relative displacement (cf. Figs. 14a and 15a) and the relative velocity at the moments of impact (Figs. 14c and 15c), as well as the diagrams of the average impact energy dissipation (cf. Figs. 14b and 15b), the corresponding bifurcation diagrams of Lyapunov exponents reveal an occurrence of wide ranges of chaos for the hard impact model, which are localized within the ranges of the period-1, period-2, period-3 and period-4 motion for the soft impact model. These differences are supposed to be caused by drastically distinct average numbers of impacts per the excitation period $a_{{\text{i}}}$ exhibited by both the models within the mentioned zones (cf. Figs. 14c and 15c). For instance, at $\eta = 3$, the value $a_{{\text{i}}} = 201$ was observed for the hard impact model, in contrast to $a_{{\text{i}}} = 2.25$ for the soft impact model. Since on the diagrams in Figs. 14b and 15b, identical degrees of the average impact energy dissipation can be observed for both the models, it can be concluded that the great majority of impacts of the hard impact model are, in fact, impacts with the relative velocity v_r close to zero. If the body is slow enough in comparison to the moving rigid base, then the base catches up with it, which results in an extra impact or even a series of impacts occurring one after another (in the real system, this behavior can be interpreted as an instantaneous continuous contact of the mass m with the base). As a consequence of these impacts, the system motion is non-periodic. Figures 16 present vibrations of the hard (Fig. 16a) and soft (Fig. 16b) impact models for η = 6.9, the relative displacement of $x_{r}$ versus time, where the symbol N on the horizontal axis denotes the number of periods of the excitation force. We can observe that in the case of an elastic base, a single slow impact corresponding to a series of slow hard impacts (a_i = 142.74) can lead to periodic motion (a_i = 0.7, z = 7/10). And this is the reason of a qualitative difference in the behavior of hard and soft impact models.

Fig. 14

Bifurcation diagrams for the system with the hard contact model with r = 0.6; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 15

Bifurcation diagrams for the system with the soft contact model with r = 0.6, k_s = 200,000; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

Fig. 16

Time diagrams for the systems and a zoom window at r = 0.6; hard contact model (a), soft contact model with k_s = 200,000 (b)

It was checked that a decrease in the value of the base stiffness coefficient from k_s = 200,000 to k_s = 2000 was not followed by any considerable differences arising between the diagrams made for those models; one could not see any significant differences in the position of ranges of the periodic motion and the values of the characteristics v_r, a_i and a_e. Due to a high similarity to the graphs in Fig. 15 for k_s = 200,000, an inclusion of the drawings for k_s = 2000 was abandoned.

A further decrease in the base stiffness coefficient k_s causes displacements of the thresholds of the low periodic behavior toward lower values of the frequency η and an occurrence of wider ranges of regular behaviors in narrower regions of chaotic motion and flatter plots of the coefficients v_r, a_i and a_e (see Fig. 17 calculated for k_s = 100).

Fig. 17

Bifurcation diagrams for the system with the soft contact model with r = 0.6, k_s = 100; the relative displacement x_r (a), the Lyapunov exponents λ₁, λ₂ (thin lines)—left axis (b) and an average value of impact energy dissipation a_e (thick line)—right axis (b), an average number of impacts a_i (thin line)—left axis (c) and the relative velocity v_r at moments of impact (points)—right axis (c)

5 Conclusions

Two different methods of impact modeling, namely hard and soft impact models, and their influence on the dynamical behavior of vibro-impact systems, in which a rigid body collides with an elastic base, are compared. The conditions ensuring the same energy losses during soft and hard impacts are derived. They enable a generation of various soft impact models equivalent to hard impact models with a given restitution coefficient, which are more widely known and studied. An introduction of impact elements of the spring-dumper type may be the only possible solution when more than two masses in series collide at the same instant. The obtained results yield the following conclusions.

For large values of the stiffness coefficient of the moving base with a low rate of energy dissipation, both models produce the same results. This agreement manifests itself in: (i) an appearance, for almost the same values of the excitation force, of chaotic motions with identical values of both the corresponding Lyapunov exponents, (ii) an existence, in a wide range of the control parameter, of periodic motions with impacts, for which the corresponding Lyapunov exponents are very close to each other, (iii) a very good conformity of the values of the corresponding relative displacements, average numbers of impacts, relative velocities at moments of impacts and average changes in kinetic energy of the body during impacts, as well as a very good conformity of the corresponding periodic phase trajectories for the hard and soft impact model.

For lower values of the stiffness coefficient of the base, when the duration of body contact cannot be neglected, as well as for large values of the stiffness coefficient of the base with a high rate of energy dissipation, when a single soft impact can correspond to a series of hard impacts, the results of both methods diverge from each other. These differences occur as a result of external forces, such as external excitation and an additional elastic-damping force, which act on the colliding body during the contact. In hard impact modeling, this effect is neglected.

In soft impact models, one has to choose two independent parameters k_s and c_s. The explicit equations presented herein allow the determination of the dumping coefficient of an impact element in terms of the stiffness coefficient and the restitution coefficient of this element. One can select these parameters as regards the contact time and the velocities before and after impact as observed in the real experiment.

When the base stiffness in the soft impact modeling is decreased, it is followed by simplification in the system behavior in a wide range of the external excitation frequency. For the same rate of energy dissipation, low periodic solutions can be observed only, which allows for suppressing chaos in real engineering systems.

Models of the system under investigation, with hard and soft impacts against a movable base and kinematic excitation, show a considerably higher sensitivity to a decrease in the stiffness of the base when compared to models with impacts on an unmovable base and with dynamic excitation.