Bifurcations in a Hamiltonian system with two degrees of freedom associated with the reversible hyperbolic umbilic

Abstract

We deal with Hamiltonian bifurcations associated with the reversible umbilic in two degrees of freedom systems defined by 0:1 resonance, i.e. the unperturbed equilibrium has two purely imaginary eigenvalues and a semisimple double-zero one. The Hamiltonian is written as the sum of integrable Hamiltonian $N\big (\frac{1}{2}(x^{2}+y^{2}),q,p;\lambda \big )$ and a small perturbation $P(x,y,q,p;\lambda )$ by the normalization procedure. The phase portrait of N on each level of the integral $I_{1}=\frac{1}{2}(x^{2}+y^{2})$ is then studied in detail, obtaining an unfolding related to the reversible hyperbolic umbilic catastrophe. The persistence of 2-tori (i.e. two-dimensional tori) for the full system is analysed via KAM theory pointed out just as in Broer et al. (Z Angew Math Phys 44: 389–432, 1993), (in: Langford, Nagata (eds) Normal forms and homoclinic chaos, Waterloo, (1992), Fields Institute Communications 4 (1995)). In a sense, our results can be seen as a four-dimensional extension of a planar problem studied by Hanßmann (Phys D 112: 81–94, 1998).

Appendices

A Appendix: Cardano’s formula for solving cubic equation

Here, we will use the Cardano’s formula to calculate the q-coordinate values of the intersection points of the q-axis and the energy curve $\Gamma$. According to (2.7), when $p=0$, the expression of the energy curve $\Gamma$ is changed to

$$\begin{aligned} E(q):=q^{3}-3\lambda _{1}q^{2}+3(\lambda _{2}+\lambda _{3}I_{1})q-3h=0, \end{aligned}$$

(A.1)

where h denotes the energy value at the point (q, 0). The square member may be removed by the substitution $q=t+\lambda _{1}$, and (A.1) can be rewritten as the canonical form of the cubic equation

$$\begin{aligned} t^{3}+mt+n=0, \end{aligned}$$

(A.2)

where

$$\begin{aligned}&m=-3\lambda _{1}^{2}+3(\lambda _{2}+\lambda _{3}I_{1}),\nonumber \\&n=3\lambda _{1} (\lambda _{2}+\lambda _{3}I_{1})-3h-2\lambda _{1}^{3}, \end{aligned}$$

(A.3)

the expression $\Delta :=\frac{1}{4}n^{2}+\frac{1}{27}m^{3}$ is called the discriminant of the cubic equation (A.2).

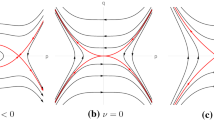
Using Cardano’s formula[11, 27] for the cubic equation (A.1), we obtain the q-coordinate values of the intersection points of the q-axis and the energy curve $\Gamma$ shown in Figs. 2 and 3 (note that in Figs. 2 and 3, we only marked some of the q-coordinate values involved in the proof of Theorems 3.5 and 3.11, while ignored other q-coordinate values). In fact, the q-coordinate value $q_{ij}(h)$ depends on the energy value h. To simplify the notation, we abbreviate $q_{ij}(h)$ as $q_{ij}$ in this appendix.

Lemma 4.1

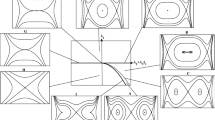
If $m=n=0(\Leftrightarrow h=h_{\eta _{+}}=h_{\eta _{-}}=\frac{1}{3}\lambda _{1}^{3})$, then the cubic equation (A.1) has one triple root, namely $q_{1,2,3}=\lambda _{1}$. This situation corresponds to the q-coordinate value of the only parabolic equilibrium point (i.e. subgraph F and subgraph H in Fig. 1) when $\lambda _{2}+\lambda _{3}I_{1}=\lambda _{1}^{2}$. Otherwise, we have the following three situations:

• (i) If $\Delta <0(\Leftrightarrow h\in (h_{\eta _{+}},h_{\eta _{-}}))$, then (A.1) has three distinct real roots, namely $q_{1i}<q_{2i}<q_{3i}$ ($i=0$ if $\lambda \in \Pi ^{A};$ $i=1,2$ if $\lambda \in \Pi ^{B}$) (cf.[10, 19]):

  $$\begin{aligned}&\left\{ \begin{array}{ll} q_{1i}=\lambda _{1}+\frac{-1+\sqrt{-1}\sqrt{3}}{2}\root 3 \of {-\frac{n}{2}+\sqrt{\Delta }}+\frac{-1-\sqrt{-1}\sqrt{3}}{2}\root 3 \of {-\frac{n}{2}-\sqrt{\Delta }}=\lambda _{1}+2\sqrt{-\frac{m}{3}}\cos (\frac{\phi }{3}+\frac{2\pi }{3})\\ q_{2i}=\lambda _{1}+\frac{-1-\sqrt{-1}\sqrt{3}}{2}\root 3 \of {-\frac{n}{2}+\sqrt{\Delta }}+\frac{-1+\sqrt{-1}\sqrt{3}}{2}\root 3 \of {-\frac{n}{2}-\sqrt{\Delta }}=\lambda _{1}+2\sqrt{-\frac{m}{3}}\cos (\frac{\phi }{3}-\frac{2\pi }{3})\\ q_{3i}=\lambda _{1}+\root 3 \of {-\frac{n}{2}+\sqrt{\Delta }}+\root 3 \of {-\frac{n}{2}-\sqrt{\Delta }}=\lambda _{1}+2\sqrt{-\frac{m}{3}}\cos \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

  (A.4)

  where

  $$\begin{aligned} \phi =\arccos \frac{-n\sqrt{-27m}}{2m^{2}} \end{aligned}$$

  (A.5)

  depends on the energy value h; 

• (ii) If $\Delta =0$ and $(m,n)\ne (0,0)(\Leftrightarrow h=h_{\eta _{-}}~\mathrm{or}~h_{\eta _{+}}~(h_{\eta _{+}}\ne h_{\eta _{-}}))$, then (A.1) has three real roots, whereby at least two of them are equal. If $h=h_{\eta _{-}}$, (A.1) has three real roots $q_{4,5}<q_{6}:$

  $$\begin{aligned} \left\{ \begin{array}{ll} q_{4,5}=\lambda _{1}+\root 3 \of {\frac{n}{2}}=\lambda _{1}-\sqrt{\lambda _{1}^{2}-(\lambda _{2}+\lambda _{3}I_{1})}:=q_{\eta _{-}}\\ q_{6}=\lambda _{1}-2\root 3 \of {\frac{n}{2}}=\lambda _{1}+2\sqrt{\lambda _{1}^{2}-(\lambda _{2}+\lambda _{3}I_{1})}; \end{array} \right. \end{aligned}$$

  If $h=h_{\eta _{+}}$, (A.1) has three real roots $q_{9}<q_{7,8}$:

  $$\begin{aligned} \left\{ \begin{array}{ll} q_{7,8}=\lambda _{1}+\root 3 \of {\frac{n}{2}}=\lambda _{1}+\sqrt{\lambda _{1}^{2}-(\lambda _{2}+\lambda _{3}I_{1})}:=q_{\eta _{+}}\\ q_{9}=\lambda _{1}-2\root 3 \of {\frac{n}{2}}=\lambda _{1}-2\sqrt{\lambda _{1}^{2}-(\lambda _{2}+\lambda _{3}I_{1})}; \end{array} \right. \end{aligned}$$

• (iii) If $\Delta >0(\Leftrightarrow h\in (-\infty ,h_{\eta _{+}})\bigcup (h_{\eta _{-}},+\infty ))$, then (A.1) has only one simple real root:

  $$\begin{aligned} q=\lambda _{1}+\root 3 \of {-\frac{n}{2}+\sqrt{\Delta }}+\root 3 \of {-\frac{n}{2}-\sqrt{\Delta }}. \end{aligned}$$

Remark 4.2

We are easy to obtain the extreme points of E(q) are $q_{\eta _{\pm }}=\lambda _{1}\pm \sqrt{\lambda _{1}^{2}-(\lambda _{2}+\lambda _{3}I_{1})}.$ It is easy to show that E(q) is strictly monotonously increasing when $q<q_{\eta _{-}}$ and $q>q_{\eta _{+}}$, strictly monotonously decreasing when $q_{\eta _{-}}<q<q_{\eta _{+}}$, and that $q_{\eta _{-}}$ and $q_{\eta _{+}}$ are the maximum and minimum points of E(q), respectively. Therefore, we imply that for the energy value $h_{\kappa }$ of the point $(q_{\kappa },0)$ on the q-axis,

$$\begin{aligned}&h_{\eta _{+}}<h_{10}=h_{20}=h_{30}<h_{\eta _{-}}=h_{6},~~~\mathrm{if} ~\lambda \in \Pi ^{A};\\&h_{\eta _{+}}<h_{1i}=h_{2i}=h_{3i}<h_{\eta _{-}},~~~i=1,2,~~~\mathrm{if} ~\lambda \in \Pi ^{B}. \end{aligned}$$

B Appendix: Some calculations involved in subsection 3.1

1.1 B.1 Formulas of $\widetilde{q}_{i0}~(i=1,2,3)$ in (3.11)

For $\lambda \in \Pi ^{A}$, we have

$$\begin{aligned} \lambda _{1}>0,~~~\frac{\lambda _{2}+\lambda _{3}I_{1}}{\lambda _{1}^{2}}=:\lambda _{A}\in (-3,1). \end{aligned}$$

(B.1)

According to Lemma 4.1 in Appendix A, the existence condition of the three q-coordinate values $q_{i0}~(i=1,2,3)$ in Case A is $h\in (h_{\eta _{+}},h_{\eta _{-}})$. From (2.5) and (B.1), it follows

$$\begin{aligned} \left\{ \begin{array}{ll} h_{\eta _{+}}=\lambda _{1}^{3}\big [-\frac{2}{3}(1-\lambda _{A})^{\frac{3}{2}}+\lambda _{A}-\frac{2}{3}\big ]:=\lambda _{1}^{3}\widetilde{h}_{\eta _{+}},\\ h_{\eta _{-}}=\lambda _{1}^{3}\big [\frac{2}{3}(1-\lambda _{A})^{\frac{3}{2}}+\lambda _{A}-\frac{2}{3}\big ]:=\lambda _{1}^{3}\widetilde{h}_{\eta _{-}}. \end{array} \right. \end{aligned}$$

(B.2)

Thus, we have

$$\begin{aligned} \lambda _{1}^{-3}h=:\widetilde{h}\in (\widetilde{h}_{\eta _{+}},\widetilde{h}_{\eta _{-}}). \end{aligned}$$

(B.3)

By (A.3) and (B.1), we can rewrite m and n as

$$\begin{aligned} m=-3\lambda _{1}^{2}(1-\lambda _{A}),~~n=\lambda _{1}^{3}(3\lambda _{A}-3\widetilde{h}-2). \end{aligned}$$

(B.4)

Noting (B.2), (B.3) and inserting (B.4) into (A.5) yields

$$\begin{aligned} \phi =\arccos \left( -n\sqrt{\frac{-27}{4m^{3}}}\right) :=\arccos F_{1}(\lambda _{A},\widetilde{h}), \end{aligned}$$

(B.5)

where

$$\begin{aligned}&F_{1}(\lambda _{A},\widetilde{h})=\frac{ \frac{3}{2}\widetilde{h} -\frac{3}{2}\lambda _{A}+1}{(1-\lambda _{A})^{\frac{3}{2}}} \\&\quad \in (F_{1}(\lambda _{A},\widetilde{h}_{\eta _{+}}),F_{1} (\lambda _{A},\widetilde{h}_{\eta _{-}}))=(-1,1). \end{aligned}$$

Therefore, $\phi \in (0,\pi )$ and depends on $\lambda _{A}$ and $\widetilde{h}$.

From Remark 3.4 and Remark 3.6, in order to prove Theorem 3.5, we need to take

$$\begin{aligned} \left\{ \begin{array}{ll} h\in (h_{1},h_{2})\subset (h_{\eta _{+}},h_{\eta _{-}}),\\ \lambda _{A}\in (-2.9,0.9)\subset (-3,1), \end{array} \right. \end{aligned}$$

(B.6)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_{1}=\lambda _{1}^{3}\big [\frac{\sqrt{2}}{3}(1-\lambda _{A})^{\frac{3}{2}}+\lambda _{A}-\frac{2}{3}\big ]:=\lambda _{1}^{3}\widetilde{h}_{1},\\ h_{2}=\lambda _{1}^{3}\big [\frac{2}{3}(1-\lambda _{A})^{\frac{3}{2}}\cos \frac{\pi }{8}+\lambda _{A}-\frac{2}{3}\big ]:=\lambda _{1}^{3}\widetilde{h}_{2}. \end{array} \right. \end{aligned}$$

(B.7)

Thus,

$$\begin{aligned} \widetilde{h}\in (\widetilde{h}_{1},\widetilde{h}_{2})\subset (\widetilde{h}_{\eta _{+}},\widetilde{h}_{\eta _{-}}). \end{aligned}$$

(B.8)

Noting (B.5)-(B.8), we have $F_{1}(\lambda _{A},\widetilde{h})\in (F_{1}(\lambda _{A},\widetilde{h}_{1}),F_{1}(\lambda _{A},\widetilde{h}_{2}))=(\frac{\sqrt{2}}{2},\cos \frac{\pi }{8})\subset (-1,1)$. Therefore, we get

$$\begin{aligned} \phi \in (\frac{\pi }{8},\frac{\pi }{4})\subset (0,\pi ) \end{aligned}$$

(B.9)

and depends on $\lambda _{A}$ and $\widetilde{h}$.

Inserting (B.4) into (A.4) yields

$$\begin{aligned} \left\{ \begin{array}{ll} \widetilde{q}_{10}=\frac{q_{10}}{\lambda _{1}}=1+2\sqrt{1-\lambda _{A}}\cos (\frac{\phi }{3}+\frac{2\pi }{3}),\\ \widetilde{q}_{20}=\frac{q_{20}}{\lambda _{1}}=1+2\sqrt{1-\lambda _{A}}\cos (\frac{\phi }{3}-\frac{2\pi }{3}),\\ \widetilde{q}_{30}=\frac{q_{30}}{\lambda _{1}}=1+2\sqrt{1-\lambda _{A}}\cos \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

(B.10)

where the expression of $\phi$ is shown in (B.5). By (B.6), (B.9) and (B.10), we have

$$\begin{aligned}&\frac{(\widetilde{q}_{20}+1)(\widetilde{q}_{20}-\widetilde{q}_{10})}{(\widetilde{q}_{30}+1)(\widetilde{q}_{30}-\widetilde{q}_{10})}\nonumber \\&\quad =\frac{\left( 1+\sqrt{1-\lambda _{A}}\cos (\frac{\phi }{3}-\frac{2\pi }{3})\right) \sin \frac{\phi }{3}}{\left( 1+\sqrt{1-\lambda _{A}}\cos \frac{\phi }{3}\right) \sin (\frac{\phi }{3}+\frac{\pi }{3})}\nonumber \\&\qquad \in (0.0112,0.1968), \end{aligned}$$

(B.11)

where we use these facts that $\cos (\frac{\phi }{3}-\frac{2\pi }{3})\in (-0.3827,-0.2590)$, $\cos \frac{\phi }{3}\in (0.9660,0.9914)$, $\sin \frac{\phi }{3}\in (0.1305,0.2586)$ and $\sin (\frac{\phi }{3}+\frac{\pi }{3})\in (0.9239,0.9659)$.

1.2 B.2 Formulas of a, b and c in (3.17) and their estimates

Noting (B.6), (B.7) and (B.8), by (A.5), (B.4) and (B.10), we can get

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial \widetilde{q}_{10}}{\partial h}=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h})\sin \left( \frac{\phi }{3}+\frac{2\pi }{3}\right) ,\\ \frac{\partial \widetilde{q}_{20}}{\partial h}=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h}) \sin \left( \frac{\phi }{3}-\frac{2\pi }{3}\right) ,\\ \frac{\partial \widetilde{q}_{30}}{\partial h}=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h})\sin \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

(B.12)

where

$$\begin{aligned}&F_{2}(\lambda _{A},\widetilde{h})=\Big [(1-\lambda _{A})^{2} -(1-\lambda _{A})^{-1}\nonumber \\&\quad \left( \frac{3}{2}\widetilde{h}-\frac{3}{2} \lambda _{A}+1\right) ^{2}\Big ]^{-\frac{1}{2}}\nonumber \\&\quad \in \left( \frac{\sqrt{2}}{1-\lambda _{A}},\frac{1}{(1-\lambda _{A}) \sqrt{1-(\cos \frac{\pi }{8})^2}}\right) \nonumber \\&\quad \subset (0.3626,26.1313)~~\mathrm{for~all}~\widetilde{h}\in \left( \widetilde{h}_{1},\widetilde{h}_{2}\right) ,\nonumber \\&\quad ~\lambda _{A}\in (-2.9,0.9). \end{aligned}$$

(B.13)

Noting (B.9), inserting (B.10), (B.12) into (3.17) and simplifying, we have

$$\begin{aligned} \left\{ \begin{array}{ll} a=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h})\sqrt{1-\lambda _{A}}f_{1}(\phi ),\\ b=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h})\big (f_{2}(\phi )+\sqrt{1-\lambda _{A}}f_{3}(\phi )\big ),\\ c=\lambda _{1}^{-3}F_{2}(\lambda _{A},\widetilde{h})\big (f_{4}(\phi )+\sqrt{1-\lambda _{A}}f_{5}(\phi )\big ), \end{array} \right. \end{aligned}$$

(B.14)

where $f_{1}(\phi ):=-6\sin (\frac{2\phi }{3}-\frac{2\pi }{3})$, $f_{2}(\phi ):=2\sqrt{3}\cos (\frac{\phi }{3}-\frac{\pi }{3})$, $f_{3}(\phi ):=4\sqrt{3}\cos (\frac{2\phi }{3}-\pi )-2\sqrt{3}\cos (\frac{2\phi }{3}+\frac{\pi }{3})$, $f_{4}(\phi ):=-2\sqrt{3}\cos \frac{\phi }{3}$ and $f_{5}(\phi ):=-2\sqrt{3}\cos (\frac{2\phi }{3}-\frac{2\pi }{3})$.

From (B.9), we can get the facts: $f_{1}(\phi )\in (5.7956,6)$, $f_{4}(\phi )\in (-3.4345,-3.3463)$, $f_{5}(\phi )\in (0.0016,0.8966)$, $f_{2}(\phi )+f_{4}(\phi )\in (-1.3257,-0.8974)$ and $f_{1}(\phi )+f_{3}(\phi )+f_{5}(\phi )\in (-0.8966,-0.0016)$. Finally, applying (B.6) and (B.13) to (B.14), we have

$$\begin{aligned} \left\{ \begin{array}{ll} a=\lambda _{1}^{-3}C_{a}>0,\\ c=\lambda _{1}^{-3}C_{c}<0,\\ a+b+c=\lambda _{1}^{-3}C_{a+b+c}<0, \end{array} \right. \end{aligned}$$

(B.15)

where

$$\begin{aligned}&C_{a}:=F_{2}(\lambda _{A},\widetilde{h})\sqrt{1-\lambda _{A}}f_{1}(\phi )\in (0.6645,309.6245),\\&C_{c}:=F_{2}(\lambda _{A},\widetilde{h})\big (f_{4}(\phi )\\&\quad +\sqrt{1-\lambda _{A}}f_{5}(\phi )\big )\in (-89.7349,-0.5713),\\&C_{a+b+c}:=F_{2}(\lambda _{A},\widetilde{h})\big [f_{2}(\phi )+f_{4}(\phi )\\&\quad +\sqrt{1-\lambda _{A}}\left( f_{1}(\phi )+f_{3}(\phi )+f_{5}(\phi )\right) \big ]\\&\quad \in (-80.9103,-0.3256). \end{aligned}$$

C. Appendix: Some calculations involved in subsection 3.2

1.1 C.1 Formulas of $\widehat{q}_{i1}~(i=1,2,3)$ in (3.34)

For $\lambda \in \Pi ^{B}$, we have

$$\begin{aligned} \mu :=-(\lambda _{2}+\lambda _{3}I_{1})>0,~~\lambda _{B}:=\frac{\lambda _{1}^{2}}{\lambda _{2}+\lambda _{3}I_{1}}\in (-\frac{1}{3},0]. \end{aligned}$$

(C.1)

According to Lemma 4.1 in Appendix A, the condition on the existence of the three q-coordinate values $q_{i1}~(i=1,2,3)$ in Case B is $h\in (h_{\mathrm{het}},h_{\eta _{-}})\subset (h_{\eta _{+}},h_{\eta _{-}})$. By (2.5) and (2.6), it follows

$$\begin{aligned} h_{\mathrm{het}}= \left\{ \begin{array}{ll} \mu ^{\frac{3}{2}}\big [-\frac{4}{3}(-\lambda _{B})^{\frac{3}{2}}+(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{\mathrm{het}}^{1}~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ \mu ^{\frac{3}{2}}\big [\frac{4}{3}(-\lambda _{B})^{\frac{3}{2}}-(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{\mathrm{het}}^{2}~~\mathrm{for}~\lambda _{1}<0, \end{array} \right. \nonumber \\ \end{aligned}$$

(C.2)

$$\begin{aligned} h_{\eta _{-}}= \left\{ \begin{array}{ll} \mu ^{\frac{3}{2}}\big [\frac{2}{3}(1-\lambda _{B})^{\frac{3}{2}}-\frac{2}{3}(-\lambda _{B})^{\frac{3}{2}}-(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{\eta _{-}}^{1}~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ \mu ^{\frac{3}{2}}\big [\frac{2}{3}(1-\lambda _{B})^{\frac{3}{2}}+\frac{2}{3}(-\lambda _{B})^{\frac{3}{2}}+(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{\eta _{-}}^{2}~~\mathrm{for}~\lambda _{1}<0. \end{array} \right. \nonumber \\ \end{aligned}$$

(C.3)

Then we have

$$\begin{aligned} \mu ^{-\frac{3}{2}}h=:\widehat{h}\in (\widehat{h}_{\mathrm{het}}^{i},\widehat{h}_{\eta _{-}}^{i})~~(i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0). \end{aligned}$$

(C.4)

By (A.3) and (C.1), we rewrite m and n as

$$\begin{aligned}&m=\mu (3\lambda _{B}-3),\nonumber \\&n= \left\{ \begin{array}{ll} \mu ^{\frac{3}{2}}\big [-3(-\lambda _{B})^{\frac{1}{2}}-3\widehat{h}-2(-\lambda _{B})^{\frac{3}{2}}\big ]~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ \mu ^{\frac{3}{2}}\big [3(-\lambda _{B})^{\frac{1}{2}}-3\widehat{h}+2(-\lambda _{B})^{\frac{3}{2}}\big ]~~\mathrm{for}~\lambda _{1}<0. \end{array} \right. \nonumber \\ \end{aligned}$$

(C.5)

By (C.1)-(C.4), inserting (C.5) into (A.5) yields

$$\begin{aligned} \phi =\left\{ \begin{array}{ll} \arccos \left( \frac{\frac{3}{2}\widehat{h}+\frac{3}{2}(-\lambda _{B})^{\frac{1}{2}}+(-\lambda _{B})^{\frac{3}{2}}}{(1-\lambda _{B})^{\frac{3}{2}}}\right) :=\arccos G_{1}^{1}(\lambda _{B},\widehat{h})~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ \arccos \left( \frac{\frac{3}{2}\widehat{h}-\frac{3}{2}(-\lambda _{B})^{\frac{1}{2}}-(-\lambda _{B})^{\frac{3}{2}}}{(1-\lambda _{B})^{\frac{3}{2}}}\right) :=\arccos G_{1}^{2}(\lambda _{B},\widehat{h})~~\mathrm{for}~\lambda _{1}<0, \end{array} \right. \end{aligned}$$

(C.6)

where

$$\begin{aligned} \left\{ \begin{array}{ll} G_{1}^{1}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{1})=\frac{3(-\lambda _{B})^{\frac{1}{2}}-(-\lambda _{B})^{\frac{3}{2}}}{(1-\lambda _{B})^{\frac{3}{2}}}\in (0,1),~~G_{1}^{1}(\lambda _{B},\widehat{h}_{\eta _{-}}^{1})\equiv 1~~\mathrm{for~all}~\lambda _{B}\in (-\frac{1}{3},0],~\lambda _{1}\geqslant 0,\\ G_{1}^{2}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{2})=\frac{-3(-\lambda _{B})^{\frac{1}{2}}+(-\lambda _{B})^{\frac{3}{2}}}{(1-\lambda _{B})^{\frac{3}{2}}}\in (-1,0),~~G_{1}^{2}(\lambda _{B},\widehat{h}_{\eta _{-}}^{2})\equiv 1~~\mathrm{for~all}~\lambda _{B}\in (-\frac{1}{3},0],~\lambda _{1}<0. \end{array} \right. \end{aligned}$$

Thus, $G_{1}^{1}(\lambda _{B},\widehat{h})\in (G_{1}^{1}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{1}),G_{1}^{1}(\lambda _{B},\widehat{h}_{\eta _{-}}^{1}))\subset (0,1),$ $G_{1}^{2}(\lambda _{B},\widehat{h})\in (G_{1}^{2}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{2}),G_{1}^{2}(\lambda _{B},\widehat{h}_{\eta _{-}}^{2}))\subset (-1,1).$ Therefore, if $\lambda _{1}\geqslant 0$, then $\phi \in (0,\frac{\pi }{2})$ and if $\lambda _{1}<0$, then $\phi \in (0,\pi )$.

From Remark 3.10 and Remark 3.12, in order to prove Theorem 3.11, we need to take

$$\begin{aligned} \left\{ \begin{array}{ll} h\in (h_{3}^{i},h_{4}^{i})\subset (h_{\mathrm{het}},h_{\eta _{-}}),\\ \lambda _{B}\in (-\frac{7}{30},0]\subset (-\frac{1}{3},0], \end{array} \right. \end{aligned}$$

(C.7)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_{3}^{i}=\mu ^{\frac{3}{2}}\widehat{h}_{3}^{i}~~(i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0),\\ h_{4}^{1}=\mu ^{\frac{3}{2}}\big [\frac{2}{3}(1-\lambda _{B})^{\frac{3}{2}}\cos \frac{\pi }{100}-\frac{2}{3}(-\lambda _{B})^{\frac{3}{2}}-(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{4}^{1}~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ h_{4}^{2}=\mu ^{\frac{3}{2}}\big [\frac{2}{3}(1-\lambda _{B})^{\frac{3}{2}}\cos \frac{\pi }{100}+\frac{2}{3}(-\lambda _{B})^{\frac{3}{2}}+(-\lambda _{B})^{\frac{1}{2}}\big ]:=\mu ^{\frac{3}{2}}\widehat{h}_{4}^{2}~~\mathrm{for}~\lambda _{1}<0, \end{array} \right. \end{aligned}$$

(C.8)

$\widehat{h}_{3}^{i}(\in (\widehat{h}_{\mathrm{het}}^{i},\widehat{h}_{4}^{i}),~i=1,2)$ are two functions depending on $\lambda _{B}$ and satisfy the condition:

$$\begin{aligned} G_{1}^{i}(\lambda _{B},\widehat{h}_{3}^{i})\in (\cos \frac{\pi }{55},\cos \frac{\pi }{100})~~\mathrm{for~all}~\lambda _{B}\in (-\frac{7}{30},0]. \end{aligned}$$

(C.9)

Thus,

$$\begin{aligned}&\widehat{h}\in (\widehat{h}_{3}^{i},\widehat{h}_{4}^{i})\subset (\widehat{h}_{\mathrm{het}}^{i},\widehat{h}_{\eta _{-}}^{i})\nonumber \\&\quad (i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0). \end{aligned}$$

(C.10)

By (C.6)-(C.10) and $G_{1}^{i}(\lambda _{B},\widehat{h}_{4}^{i})\equiv \cos \frac{\pi }{100}~(i=1,2)$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} G_{1}^{1}(\lambda _{B},\widehat{h})\in (G_{1}^{1}(\lambda _{B},\widehat{h}_{3}^{1}),G_{1}^{1}(\lambda _{B},\widehat{h}_{4}^{1}))\subset (\cos \frac{\pi }{55},\cos \frac{\pi }{100})\subset (0,1)~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ G_{1}^{2}(\lambda _{B},\widehat{h})\in (G_{1}^{2}(\lambda _{B},\widehat{h}_{3}^{2}),G_{1}^{2}(\lambda _{B},\widehat{h}_{4}^{2}))\subset (\cos \frac{\pi }{55},\cos \frac{\pi }{100})\subset (-1,1)~~\mathrm{for}~\lambda _{1}<0. \end{array} \right. \end{aligned}$$

Therefore, for all $\lambda _{1}\in \mathbb {R}^{1}$ and $\lambda _{B}\in (-\frac{7}{30},0]$, we have

$$\begin{aligned} \phi \in (\frac{\pi }{100},\frac{\pi }{55})\subset (0,\frac{\pi }{2}) \end{aligned}$$

(C.11)

and depends on $\lambda _{B}$ and $\widetilde{h}$.

Substituting (C.5) into (A.4) gives that if $\lambda _{1}\geqslant 0$, then

$$\begin{aligned} \left\{ \begin{array}{ll} \widehat{q}_{11}=\mu ^{-\frac{1}{2}}q_{11}=(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}+\frac{2\pi }{3}),\\ \widehat{q}_{21}=\mu ^{-\frac{1}{2}}q_{21}=(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}-\frac{2\pi }{3}),\\ \widehat{q}_{31}=\mu ^{-\frac{1}{2}}q_{31}=(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

(C.12)

and if $\lambda _{1}<0$, then

$$\begin{aligned} \left\{ \begin{array}{ll} \widehat{q}_{11}=\mu ^{-\frac{1}{2}}q_{11}=-(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}+\frac{2\pi }{3}),\\ \widehat{q}_{21}=\mu ^{-\frac{1}{2}}q_{21}=-(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}-\frac{2\pi }{3}),\\ \widehat{q}_{31}=\mu ^{-\frac{1}{2}}q_{31}=-(-\lambda _{B})^{\frac{1}{2}}+2\sqrt{1-\lambda _{B}}\cos \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

(C.13)

where the expression of $\phi$ is given in (C.6). Due to (C.7), (C.11)-(C.13) and facts $\cos (\frac{\phi }{3}-\frac{2\pi }{3})\in (-0.4909,-0.4834)$, $\cos (\frac{\phi }{3}+\frac{2\pi }{3})\in (-0.5164,-0.5090)$, $\sin (\frac{\phi }{3}-\frac{\pi }{3})\in (-0.8607,-0.8563)$ and $\sin (\frac{\phi }{3}+\frac{\pi }{3})\in (0.8712,0.8754)$, it is easy to obtain that

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{(\widehat{q}_{21}+(-\lambda _{B})^{\frac{1}{2}})(\widehat{q}_{21}-\widehat{q}_{31})}{(\widehat{q}_{11}+(-\lambda _{B})^{\frac{1}{2}})(\widehat{q}_{11}-\widehat{q}_{31})}=\frac{\left[ (-\lambda _{B})^{\frac{1}{2}}+\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}-\frac{2\pi }{3})\right] \sin (\frac{\phi }{3}-\frac{\pi }{3})}{-\big [(-\lambda _{B})^{\frac{1}{2}}+\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}+\frac{2\pi }{3})\big ]\sin (\frac{\phi }{3}+\frac{\pi }{3})}\in (6.8217\times 10^{-4},20.6696)~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ \frac{(\widehat{q}_{21}-(-\lambda _{B})^{\frac{1}{2}})(\widehat{q}_{21}-\widehat{q}_{31})}{(\widehat{q}_{11}-(-\lambda _{B})^{\frac{1}{2}})(\widehat{q}_{11}-\widehat{q}_{31})}=\frac{\left[ -(-\lambda _{B})^{\frac{1}{2}}+\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}-\frac{2\pi }{3})\right] \sin (\frac{\phi }{3}-\frac{\pi }{3})}{-\big [-(-\lambda _{B})^{\frac{1}{2}}+\sqrt{1-\lambda _{B}}\cos (\frac{\phi }{3}+\frac{2\pi }{3})\big ]\sin (\frac{\phi }{3}+\frac{\pi }{3})}\in (0.4475,1.9959)~~\mathrm{for}~\lambda _{1}<0. \end{array} \right. \end{aligned}$$

(C.14)

1.2 C.2 Formulas of $a_{i},b_{i}$ and $c_{i}~(i=1,2)$ in (3.40)–(3.42) and their estimates

By (A.3), (A.5), (C.5), differentiating (C.12) (and (C.13)) with respect to h and simplifying the equalities, we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial \widehat{q}_{11}}{\partial h}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\sin (\frac{\phi }{3}+\frac{2\pi }{3}),\\ \frac{\partial \widehat{q}_{21}}{\partial h}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\sin (\frac{\phi }{3}-\frac{2\pi }{3}),\\ \quad (i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0))\\ \frac{\partial \widehat{q}_{31}}{\partial h}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\sin \frac{\phi }{3}, \end{array} \right. \end{aligned}$$

(C.15)

where

$$\begin{aligned}&\left\{ \begin{array}{ll} G_{2}^{1}(\lambda _{B},\widehat{h})=\Big [(1-\lambda _{B})^{2}-(1-\lambda _{B})^{-1}\left( \frac{3}{2}\widehat{h}+\frac{3}{2}(-\lambda _{B})^{\frac{1}{2}}+(-\lambda _{B})^{\frac{3}{2}}\right) ^{2}\Big ]^{-\frac{1}{2}}~~\mathrm{for}~\lambda _{1}\geqslant 0,\\ G_{2}^{2}(\lambda _{B},\widehat{h})=\Big [(1-\lambda _{B})^{2}-(1-\lambda _{B})^{-1}\left( \frac{3}{2}\widehat{h}-\frac{3}{2}(-\lambda _{B})^{\frac{1}{2}}-(-\lambda _{B})^{\frac{3}{2}}\right) ^{2}\Big ]^{-\frac{1}{2}}~~\mathrm{for}~\lambda _{1}<0. \end{array} \right. \end{aligned}$$

Combining (C.2), (C.7) and (C.8), we have

$$\begin{aligned}&\left\{ \begin{array}{ll} G_{2}^{i}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{i})=\Big [(1-\lambda _{B})^{2}-(1-\lambda _{B})^{-1}\left( 3(-\lambda _{B})^{\frac{1}{2}}-(-\lambda _{B})^{\frac{3}{2}}\right) ^{2}\Big ]^{-\frac{1}{2}}\in ( 1, 3.7019),\\ G_{2}^{i}(\lambda _{B},\widehat{h}_{4}^{i})=\frac{1}{(1-\lambda _{B})\sqrt{1-(\cos \frac{\pi }{100})^2}}\in (25.8132,31.8362) \end{array} \right. \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0). \end{aligned}$$

Thus,

$$\begin{aligned}&G_{2}^{i}(\lambda _{B},\widehat{h})\in (G_{2}^{i}(\lambda _{B},\widehat{h}_{3}^{i}),\nonumber \\&\quad G_{2}^{i}(\lambda _{B},\widehat{h}_{4}^{i}))\subset (G_{2}^{i}(\lambda _{B},\widehat{h}_{\mathrm{het}}^{i}),G_{2}^{i}(\lambda _{B},\widehat{h}_{4}^{i}))\subset (1,31.8362) \nonumber \\&~~~~~~\mathrm{for~all}~\widehat{h}\in (\widehat{h}_{3}^{i},\widehat{h}_{4}^{i})~{\mathrm{and}}~\lambda _{B}\in (-\frac{7}{30},0]\nonumber \\&\quad (i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0). \end{aligned}$$

(C.16)

Noting (C.11), inserting (C.12) (or (C.13)), (C.15) into (3.40)-(3.42), we have

$$\begin{aligned} \left\{ \begin{array}{ll} a_{i}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\sqrt{1-\lambda _{B}}g_{1}^{i}(\phi ),\\ b_{i}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\left( (-\lambda _{B})^{\frac{1}{2}}g_{2}^{i}(\phi )+\sqrt{1-\lambda _{B}}g_{3}^{i}(\phi )\right) ,\\ \quad (i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0)\\ c_{i}=\mu ^{-\frac{3}{2}}G_{2}^{i}(\lambda _{B},\widehat{h})\left( (-\lambda _{B})^{\frac{1}{2}}g_{4}^{i}(\phi )+\sqrt{1-\lambda _{B}}g_{5}^{i}(\phi )\right) ,\\ \end{array} \right. \end{aligned}$$

(C.17)

where $g_{1}^{1}(\phi )=g_{1}^{2}(\phi ):=-6\sin \frac{2\phi }{3}\in ( -0.2284,-0.1257)$, $g_{2}^{1}(\phi ):=-2\sqrt{3}\cos \frac{\phi }{3}\in ( -3.4639, -3.4635)$, $g_{2}^{2}(\phi )=-g_{2}^{1}(\phi )\in ( 3.4635, 3.4639)$, $g_{3}^{1}(\phi )=g_{3}^{2}(\phi ):=-4\sqrt{3}\cos (\frac{2\phi }{3}-\frac{2\pi }{3})-2\sqrt{3}\cos \frac{2\phi }{3}\in (-0.2284, -0.1257)$, $g_{4}^{1}(\phi ):=-2\sqrt{3}\cos (\frac{\phi }{3}-\frac{\pi }{3})\in ( -1.7888, -1.7634)$, $g_{4}^{2}(\phi )=-g_{4}^{1}(\phi )\in (1.7634, 1.7888)$ and $g_{5}^{1}(\phi )=g_{5}^{2}(\phi ):=-2\sqrt{3}\cos (\frac{2\phi }{3}-\pi )\in (3.4616,3.4633)$.

Applying (C.7) and (C.16) to (C.17), we have

$$\begin{aligned} \left\{ \begin{array}{ll} a_{i}=\mu ^{-\frac{3}{2}}C_{a_{i}}<0,\\ c_{i}=\mu ^{-\frac{3}{2}}C_{c_{i}}>0, &{}\quad (i=1~\mathrm{if}~\lambda _{1}\geqslant 0;~i=2~\mathrm{if}~\lambda _{1}<0),\\ a_{i}-b_{i}+c_{i}=\mu ^{-\frac{3}{2}}C_{a_{i}-b_{i}+c_{i}}>0, \end{array} \right. \end{aligned}$$

(C.18)

where

$$\begin{aligned}&C_{a_{1}}:=G_{2}^{1}(\lambda _{B},\widehat{h})\sqrt{1-\lambda _{B}}g_{1}^{1}(\phi )\in (-8.0756,-0.1257),\\&C_{a_{2}}:=G_{2}^{2}(\lambda _{B},\widehat{h})\sqrt{1-\lambda _{B}}g_{1}^{2}(\phi )\in (-8.0756,-0.1257),\\&C_{c_{1}}:=G_{2}^{1}(\lambda _{B},\widehat{h})\big ((-\lambda _{B})^{\frac{1}{2}}g_{4}^{1}(\phi )\\&\quad +\sqrt{1-\lambda _{B}}g_{5}^{1}(\phi )\big )\in (1.9536,122.4529),\\&C_{c_{2}}:=G_{2}^{2}(\lambda _{B},\widehat{h})\big ((-\lambda _{B})^{\frac{1}{2}}g_{4}^{2}(\phi )\\&\quad +\sqrt{1-\lambda _{B}}g_{5}^{2}(\phi )\big )\in (3.4616,170.4605),\\&C_{a_{1}-b_{1}+c_{1}}:=G_{2}^{1}(\lambda _{B},\widehat{h})\big [(-\lambda _{B})^{\frac{1}{2}}(-g_{2}^{1}(\phi )+g_{4}^{1}(\phi ))\\&\quad +\sqrt{1-\lambda _{B}}\left( g_{1}^{1}(\phi )-g_{3}^{1}(\phi )+g_{5}^{1}(\phi )\right) \big ]\\&\in (3.4616,168.0908),\\&C_{a_{2}-b_{2}+c_{2}}:=G_{2}^{2}(\lambda _{B},\widehat{h})\big [(-\lambda _{B})^{\frac{1}{2}}(-g_{2}^{2}(\phi )+g_{4}^{2}(\phi ))\\&\quad +\sqrt{1-\lambda _{B}}\left( g_{1}^{2}(\phi )-g_{3}^{2}(\phi )+g_{5}^{2}(\phi )\right) \big ]\\&\in (2.0281,122.4529). \end{aligned}$$

D Appendix: A KAM theorem for nearly integrable Hamiltonian systems

Consider the following Hamiltonian systems

$$\begin{aligned} \frac{{\mathrm {d}}q}{{\mathrm {d}}t}=\frac{\partial H}{\partial p},~~\frac{{\mathrm {d}}p}{{\mathrm {d}}t}=-\frac{\partial H}{\partial q}, \end{aligned}$$

(D.1)

with Hamiltonian $H(q,p)=h(p)+\varepsilon f(q,p)$, $(q,p)\in \mathbb {T}^{n} \times D$, $n\geqslant 2$, where $p=(p_{1},p_{2},\ldots ,p_{n})$ are action variables in some bounded connected domain $D\subset \mathbb {R}^{n}$, and $q=(q_{1},q_{2},\ldots ,q_{n})\in \mathbb {T}^{n}:=\mathbb {R}^{n}/(2\pi \mathbb {Z})^{n}$ are conjugate angular variables.

Lemma 4.3

[28, Theorem A] Suppose that $H(q,p)=h(p)+\varepsilon f(q,p)$ is analytic in $\mathbb {T}^{n}\times \overline{D}$, where $\overline{D}$ is the closure of D. If for each $p\in D$

$$\begin{aligned} {\mathrm{rank}}\left\{ \omega ,\frac{\partial ^{\mid k\mid }\omega }{\partial p^{k}}\big |\forall k\in \mathbb {Z}_{+}^{n},|k|\leqslant n-1\right\} =n, \end{aligned}$$

(D.2)

where $\omega (p)=\frac{\partial h(p)}{\partial p}$ and $\frac{\partial ^{\mid k\mid }\omega }{\partial p^{k}}=(\frac{\partial ^{\mid k\mid }\omega _{1}}{\partial p^{k}},\frac{\partial ^{\mid k\mid }\omega _{2}}{\partial p^{k}},\ldots ,\frac{\partial ^{\mid k\mid }\omega _{n}}{\partial p^{k}})$, then for $\forall \gamma >0$ sufficiently small, there exists $\varepsilon _{0}=\varepsilon _{0}(\gamma )>0$ such that if $|\varepsilon |<\varepsilon _{0}$, there exists a nonempty Cantorian-like subset $D_{\gamma }\subset D$ such that (D.1) admits a family of invariant n-tori $\{{\mathcal {T}}_{p}^{n} : p\in D_{\gamma }\}$, whose frequencies $\omega _{*}(p)$ satisfy $|\omega _{*}(p)-\omega (p)|\leqslant c\varepsilon$ with c being a constant independent of $\varepsilon$. Moreover, $\mathrm{Meas}(D\backslash D_{\gamma })=O(\gamma )$, where $O(\gamma )\rightarrow 0$ as $\gamma \rightarrow 0$.