1 Introduction

In the present article, we study a two-body problem with quick loss of mass which was proposed by Verhulst in [14]:

$$\begin{aligned} \ddot{x}+x&=u, \end{aligned}$$
(1a)
$$\begin{aligned} \varepsilon \dot{u}&=-f(t,x,\dot{x},\varepsilon )u^n, \end{aligned}$$
(1b)

with initial conditions

$$\begin{aligned} x(0)=x_0,\quad \dot{x}(0)=y_0,\quad \text {and}\quad u(0)=u_0>0. \end{aligned}$$
(2)

Here, the dot denotes differentiation with respect to time \(t\in \mathbb {R}^+\), while \(0<\varepsilon \ll 1\) is a small parameter and \(n>1\) is a real exponent. The function f is assumed to be continuously differentiable in \((t,x,\dot{x},\varepsilon )\) with bounded derivatives for \(t\in [0,L]\), where L is a positive, \(\varepsilon \)-independent constant; moreover, it may be assumed that

$$\begin{aligned}&0<m<f(t,x,\dot{x},\varepsilon )\qquad \text {for all }(t,x,\dot{x},\varepsilon )\in \mathbb {R}^+\nonumber \\&\quad \times \mathbb {R}^2\times [0,\varepsilon _0], \end{aligned}$$
(3)

with m and \(\varepsilon _0\) constant.

Equation (1) arises in the study of modifications of the classical two-body problem from celestial mechanics, such as in the modelling of binary stars with rapid loss of mass. There, the two stars interact by Newtonian gravitational forces, whereby their motion is confined to a plane by conservation of momentum, with mass being ejected isotropically. The variables x and t are then associated with \(r^{-1}\) and \(\theta \), respectively, in that orbital plane, where \((r,\theta )\) denotes standard polar coordinates. The variable u represents the total mass in the system; crucially, the large parameter \(\varepsilon ^{-1}\) encodes the initial rate of loss of mass, while the exponent n in (1b) determines the rate at which mass decays in time. For a detailed derivation of Eq. (1), the reader is referred to [13].

Equation (1) represents a classical singular perturbation problem that exhibits a boundary layer at \(u=0\) due to the presence of the small parameter \(\varepsilon \) in (1b). Correspondingly, in [14], Verhulst derives asymptotic solution expansions for (1) by applying matched asymptotics in the formulation of Vasil’eva [12], as well as the method of multiple scales that is due to O’Malley [9]. In the process, he observes that the case where \(n=2\) in (1b) is distinguished due to the presence of logarithmic (“switchback”) terms in \(\varepsilon \) in the resulting expansions for \((x,\dot{x})(t)\).

Here, we showcase how the classical asymptotic analysis of the boundary layer problem in Eq. (1), as presented in [14], can be re-interpreted within a dynamical systems framework. Specifically, we combine the geometric singular perturbation theory due to Fenichel [5] with the desingularization technique known as “blow-up” [4] to obtain rigorous asymptotic expansions for (1). In particular, we identify the reason for why the case of \(n=2\) in (1b) is distinguished, and we justify rigorously the structure of the corresponding expansions via a resonance phenomenon in one of the coordinate charts after blow-up. For definiteness, we focus on the case where \(f\equiv 1\) in Eq. (1) which was also considered by Verhulst [14]. As will become apparent in the following, that choice of f allows for a relatively explicit analysis while being representative of the asymptotics of (1) under the more general assumption in Eq. (3).

The article is structured as follows. In Sect. 2, we formulate the fast-slow system in standard form on which our analysis is based. In Sect. 3, we introduce the blow-up transformation which allows us to desingularize the flow of that system; in particular, we construct a singular orbit \(\Gamma \), and we show the persistence thereof for \(\varepsilon \) sufficiently small. In Sect. 4, we derive asymptotic solution expansions for our system; we discuss the resonant case where \(n=2\), and we compare our results with those of Verhulst [14]. Finally, we conclude in Sect. 5 with a summary, and an outlook to potential future research.

2 Fast-slow analysis

In this section, we reformulate Eq. (1) as a first-order system of ordinary differential equations that is amenable to our geometric approach: we introduce the new variable \(y=\dot{x}\) in Eq. (1) to obtain

$$\begin{aligned}&\dot{x} =y, \end{aligned}$$
(4a)
$$\begin{aligned}&\dot{y} =u-x, \end{aligned}$$
(4b)
$$\begin{aligned}&\varepsilon \dot{u} =-f(t,x,y,\varepsilon )u^n, \end{aligned}$$
(4c)

which will be the starting point for our analysis. Given our assumption in (3), Eq. (4) has a unique steady state at the origin in (x, y, u)-space. Henceforth, we will assume that for \(t\in \mathbb {R}^+\), the dynamics of (4) evolves on a compact set \(D:=[-X,X]\times [-Y,Y]\times [-U,U]\subset \mathbb {R}\), with X, Y, and U positive and sufficiently large; in particular, \((0,0,0)\in D\).

Equation (4) is a fast-slow system in standard form, written on the slow time scale t, where (x, y) are slow variables and u is fast; the corresponding fast system on the fast time scale \(\tau =\frac{t}{\varepsilon }\) takes the form

$$\begin{aligned} x'&=\varepsilon y, \end{aligned}$$
(5a)
$$\begin{aligned} y'&=\varepsilon (u-x), \end{aligned}$$
(5b)
$$\begin{aligned} u'&=-f(\varepsilon \tau ,x,y,\varepsilon )u^n, \end{aligned}$$
(5c)

where the prime denotes differentiation with respect to \(\tau \).

Setting \(\varepsilon =0\) in Eqs. (4) and (5) yields two limiting systems, the “reduced problem”

$$\begin{aligned} \dot{x}&=y, \end{aligned}$$
(6a)
$$\begin{aligned} \dot{y}&=u-x, \end{aligned}$$
(6b)
$$\begin{aligned} 0&=-f(t,x,y,0)u^n \end{aligned}$$
(6c)

and the “layer problem”

$$\begin{aligned} x'&=0, \end{aligned}$$
(7a)
$$\begin{aligned} y'&=0, \end{aligned}$$
(7b)
$$\begin{aligned} u'&=-f(0,x,y,0)u^n. \end{aligned}$$
(7c)

The critical manifold for Eq. (6), which we denote by \(\mathcal {S}\), is obtained from (6c): since f is bounded away from zero, by Eq. (3), \(\mathcal {S}\) is given by \(\{u=0\}\), i.e., by the (x, y)-plane; linearization of (7c) gives

$$\begin{aligned}&\frac{\partial }{\partial u}\big [-f(0,x,y,0)u^n\big ]\Big |_{\{u=0\}}\nonumber \\&\quad =-nf(0,x,y,0)u^{n-1}\Big |_{\{u=0\}}=0 \end{aligned}$$
(8)

due to \(n>1\). Hence, the manifold \(\mathcal {S}\) is not normally hyperbolic; in other words, the mass u of the system decays to zero algebraically in time, rather than exponentially. (We emphasize that \(\mathcal {S}\) is still weakly attracting, as well as that the decrease in u is monotonic, by (7c).) It follows that standard geometric singular perturbation theory [5, 6] is not applicable; to remedy the loss of normal hyperbolicity, we apply the blow-up technique in its formulation due to [4, 7]. (For the reader’s reference, the “regular” case where \(n=1\) in Eq. (4) is discussed briefly in Appendix A.)

Throughout the remainder of the article, we restrict to the case where \(f\equiv 1\) in (4): given that f is uniformly bounded away from zero in general, by (3), other choices of f can be considered in a similar fashion; details can be found in Sect. 5. Under that restriction, the general solution to Eqs. (6) and (7) then reads

$$\begin{aligned} x(t)&=x_0\cos (t)+y_0\sin (t), \end{aligned}$$
(9a)
$$\begin{aligned} y(t)&=y_0\cos (t)-x_0 \sin (t), \end{aligned}$$
(9b)
$$\begin{aligned} u(t)&=0 \end{aligned}$$
(9c)

and

$$\begin{aligned} x(\tau )&=x_0, \end{aligned}$$
(10a)
$$\begin{aligned} y(\tau )&=y_0, \end{aligned}$$
(10b)
$$\begin{aligned} u(\tau )&=\big [(n-1)\tau +u_0^{1-n}\big ]^{\frac{1}{1-n}}, \end{aligned}$$
(10c)

respectively. In particular, the solution of the reduced problem in (9) is usually known as the (leading-order) “outer” solution, while the solution to the layer problem in (10) is referred to as the “inner” solution. However, for \(\varepsilon \) positive and sufficiently small, neither solution perturbs to a uniformly valid solution for Eq. (4); that deficiency is traditionally overcome by asymptotic matching in an “intermediate” region. Equation (4) is hence naturally studied in three regions I, II, and III; here, regions I and III correspond to the inner and outer regions, respectively, in the language of matched asymptotics, while region II represents the overlap between those two regions. We emphasize that, while the manifold \(\mathcal {S}\) is non-hyperbolic, the existence of a slow manifold \(\mathcal {S}_\varepsilon \equiv \mathcal {S}\) follows from the invariance of \(\mathcal {S}\) for any \(\varepsilon \). (Correspondingly, Eq. (9) then also gives the exact solution to (4) on \(\mathcal {S}_\varepsilon \) for arbitrary \(\varepsilon \in [0,\varepsilon _0]\).) Therefore, blow-up does not yield the existence of \(\mathcal {S}_\varepsilon \) in our case; rather, it will allow us to desingularize the flow of Eq. (4) in the vicinity of \(\mathcal {S}_\varepsilon \), i.e., in regions II and III, and to justify rigorously the small-\(\varepsilon \) asymptotics derived in [13] .

Fig. 1
figure 1

Numerical simulation of Eq. (4) for varying n and \(\varepsilon \), \(t\in [0,35]\), \(f\equiv 1\), and initial condition \((x_0,y_0,u_0)=(1.5,1,2)\)

Full size image
Fig. 2
figure 2

Numerical simulation of Eq. (4) for varying n and \(\varepsilon \), \(t\in [0,35]\), \(f(x)=2+\cos (x)\) (top row), \(f(y)=1+\mathrm{e}^{-y^2}\) (middle row), \(f(t)=1+10t^2\) (bottom row), and initial condition \((x_0,y_0,u_0)=(1.5,1,2)\)

Full size image

In Fig. 1, we visualize the fast-slow dynamics of Eq. (4) for various values of n and \(\varepsilon \) and \(f\equiv 1\); the intermediate time scale which is observed is due to the non-hyperbolicity of \(\mathcal {S}_\varepsilon \), and the resulting algebraic decay of u, for \(n>1\). Figure 2 shows dynamics with different choices of f in (4); comparison with Fig. 1 indicates that the dependence of f on x, y, and t, respectively, does not affect the qualitative dynamics of Eq. (4).

Remark 1

In [14], Tikhonov’s theorem [15, Theorem 8.1] is applied to show that, for \(\varepsilon \rightarrow 0\), solutions of Eq. (4) converge to those of the reduced problem, Eq. (6), uniformly in time (t). In particular, the resulting leading-order outer approximation for the corresponding solution to (4) agrees with Eq. (9) above. Here, we will argue that convergence to \(\mathcal {S}_\varepsilon \) under the fast flow of Eq. (5) is, in fact, exponential in suitably chosen “blow-up” coordinates.

2.1 Dynamics in region I

We begin by considering the dynamics in region I, where \(u=\mathcal {O}(1)\); to that end, we first append the trivial equation \(\varepsilon '=0\) to (5), where we recall that \(f\equiv 1\):

$$\begin{aligned} x'&=\varepsilon y, \end{aligned}$$
(11a)
$$\begin{aligned} y'&=\varepsilon (u-x), \end{aligned}$$
(11b)
$$\begin{aligned} u'&=-u^n, \end{aligned}$$
(11c)
$$\begin{aligned} \varepsilon '&=0. \end{aligned}$$
(11d)

For \(\varepsilon \in (0,\varepsilon _0]\) fixed, with \(\varepsilon _0\) sufficiently small, the steady states of Eq. (11) are now found at \(Q_{\varepsilon }^+:\ (0,0,0,\varepsilon )\); for future reference, we define the corresponding line of steady states by \(\ell ^+:=\big \{ (0,0,0,\varepsilon ) \, \big | \, \varepsilon \in [0,\varepsilon _0] \big \}\). (For \(\varepsilon =0\), any point on the critical manifold \(\mathcal {S}\) is also a steady state, as required.)

In the singular limit as \(\varepsilon \rightarrow 0\), Eq. (11) reduces to

$$\begin{aligned} x'&=0, \end{aligned}$$
(12a)
$$\begin{aligned} y'&=0, \end{aligned}$$
(12b)
$$\begin{aligned} u'&=-u^n, \end{aligned}$$
(12c)
$$\begin{aligned} \varepsilon '&=0; \end{aligned}$$
(12d)

given the initial state \(Q^-:\ (x_0,y_0,u_0,0)\), recall (2), we easily obtain the general solution to (12), as given in Sect. 2. Let us now introduce the following notation: we denote by \(\Sigma ^{\mathrm{in}}\) the hyperplane \(\{u=r_0\}\) in \((x,y,u,\varepsilon )\)-space, where \(r_0>0\) is chosen sufficiently small, but fixed, i.e., we choose \(\Sigma ^{\mathrm{in}}\) to define the boundary between regions I and II. In particular, since \(r_0<u_0\) and as u is monotonically decreasing in \(\tau \), by (7c), we may determine the time \(\tau ^{\mathrm{in}}>0\) such that \(u(\tau ^{\mathrm{in}})=r_0\):

$$\begin{aligned} \tau ^{\mathrm{in}}=\frac{1}{n-1}\big (r_0^{1-n}-u_0^{1-n}\big ). \end{aligned}$$
(13)

Hence, the segment \(\Gamma ^{\mathrm{I}}\) of the singular orbit \(\Gamma \) in region I can be written as follows:

$$\begin{aligned}&\Gamma ^{\mathrm{I}}:=\big \{ (x,y,u,0) \, \big | \, x=x(\tau ), y=y(\tau ),\ \text {and}\nonumber \\&\quad u=u(\tau )\ \text {for}\ \tau \in [0,\tau ^{\mathrm{in}}] \big \}, \end{aligned}$$
(14)

where \((x,y,u)(\tau )\) are as stated in Eq. (10) and \(\tau ^{\mathrm{in}}\) is defined in (13). Moreover, we label the point of intersection of \(\Gamma ^{\mathrm{I}}\) with \(\Sigma ^{\mathrm{in}}\) as \(P^{\mathrm{in}}:\ (x_0,y_0,r_0,0)\).

Next, we study the persistence of the orbit \(\Gamma ^{\mathrm{I}}\), for \(\varepsilon \) positive and sufficiently small. Correspondingly, we denote by \(Q_\varepsilon ^-:\ (x_0,y_0,u_0,\varepsilon )\) the initial point for the flow of Eq. (11), with \(\varepsilon \) fixed; finally, we define the corresponding line of initial states in the extended \((x,y,u,\varepsilon )\)-space as \(\ell ^-:=\big \{ (x_0,y_0,u_0,\varepsilon ) \, \big | \, \varepsilon \in [0,\varepsilon _0] \big \}\).

By regular perturbation theory, \(\Gamma ^{\mathrm{I}}\) will persist as an orbit \(\Gamma _\varepsilon ^{\mathrm{I}}\) that is initiated in \(Q_\varepsilon ^-\): for \(n\ne 2\), we find

$$\begin{aligned} x(\tau ,\varepsilon )&=x_0+\varepsilon y_0\tau +\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(15a)
$$\begin{aligned} y(\tau ,\varepsilon )&=y_0-\varepsilon \bigg \{x_0\tau -\frac{\big [(n-1)\tau +u_0^{1-n}\big ]^{1+\frac{1}{1-n}}}{n-2}\nonumber \\&\quad -\frac{u_0^{2-n}}{n-2}\bigg \}+\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(15b)

whereas for \(n=2\), we have

$$\begin{aligned} x(\tau ,\varepsilon )&=x_0+\varepsilon y_0\tau +\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(16a)
$$\begin{aligned} y(\tau ,\varepsilon )&=y_0-\varepsilon [x_0\tau -\ln (1+u_0\tau )]+\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(16b)

which, together with (10c), implies that, for \(\varepsilon \) fixed, \(\Gamma _\varepsilon ^{\mathrm{I}}\) is given by

$$\begin{aligned}&\Gamma _\varepsilon ^{\mathrm{I}}:=\big \{ (x,y,u,\varepsilon ) \, \big | \, x=x(\tau ,\varepsilon ), y=y(\tau ,\varepsilon ),\ \text {and}\nonumber \\&\quad u=u(\tau )\ \text {for}\ \tau \in [0,\tau ^{\mathrm{in}}]\ \text {and}\ \varepsilon \in (0,\varepsilon _0] \big \}; \end{aligned}$$
(17)

here, \(x(\tau ,\varepsilon )\) and \(y(\tau ,\varepsilon )\) are defined in (15) and (16) for \(n\ne 2\) and \(n=2\), respectively, while \(u(\tau )\) is as in (10c). (We remark that we have stated explicitly the \(\varepsilon \)-dependence of x and y, for clarity.)

Remark 2

We note that the union \(\bigcup _{\varepsilon \in [0,\varepsilon _0]}\Gamma _\varepsilon ^{\mathrm{I}}\) defines a manifold in \((x,y,u,\varepsilon )\)-space, which is hence tracked from the inner region I into the outer region III via the intermediate region II. However, for ease of comparison with [13], we will take an orbit-focused approach in the following.

Finally, we define the point of intersection of \(\Gamma _\varepsilon ^{\mathrm{I}}\) with \(\Sigma ^{\mathrm{in}}\) as \(P_\varepsilon ^{\mathrm{in}}:\ (x^{\mathrm{in}},y^{\mathrm{in}},r_0,\varepsilon )\); given Eqs. (15) and (16), respectively, we find

$$\begin{aligned} \begin{aligned} x^{\mathrm{in}}&=x_0+\varepsilon \frac{y_0}{n-1}\big (r_0^{1-n}-u_0^{1-n}\big )+\mathcal {O}(\varepsilon ^2)\quad \text {and}\\ y^{\mathrm{in}}&=y_0-\varepsilon \Big [\frac{x_0}{n-1}\big (r_0^{1-n}-u_0^{1-n}\big )-\frac{r_0^{2-n}-u_0^{2-n}}{n-2}\Big ]\\&\quad +\mathcal {O}(\varepsilon ^2) \end{aligned} \end{aligned}$$
(18)

for \(n\ne 2\), as well as

$$\begin{aligned}&x^{\mathrm{in}}=x_0+\varepsilon y_0\big (r_0^{-1}-u_0^{-1}\big )+\mathcal {O}(\varepsilon ^2)\quad \text {and}\nonumber \\&\quad y^{\mathrm{in}}=y_0-\varepsilon \Big [x_0\big (r_0^{-1}-u_0^{-1}\big )-\ln \frac{u_0}{r_0}\Big ]+\mathcal {O}(\varepsilon ^2) \end{aligned}$$
(19)

for \(n=2\), respectively. (Here, \(x^{\mathrm{in}}=x(\tau ^{\mathrm{in}},\varepsilon )\) and \(y^{\mathrm{in}}=y(\tau ^{\mathrm{in}},\varepsilon )\), where \(\tau ^{\mathrm{in}}\) is defined as in Eq. (13).)

Remark 3

Equations (15) and (16) correspond to Eqs. (17) through (19) and (24) through (26), respectively, in [14].

3 Geometric desingularization

In this section, we desingularize the dynamics in a neighborhood of the critical manifold \(\mathcal {S}\) for Eq. (11). Our analysis will proceed in two steps: first, we will blow up the (x, y)-plane in the extended \((x,y,u,\varepsilon )\)-space, which will allow us to give a rigorous description of the dynamics for \(\varepsilon =0\); in particular, we will define a singular orbit \(\Gamma \) in that limit. The dynamics that is obtained in the various coordinate charts will then be combined into a global description of the flow of Eq. (11) near the degenerate (x, y)-plane which is uniformly valid in \(\varepsilon \), and which hence shows the persistence of \(\Gamma \) for \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0\) positive and sufficiently small.

We introduce the quasi-homogeneous blow-up transformation \(\Phi :\ B\rightarrow \mathbb {R}^4\) in Eq. (11):

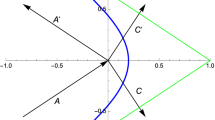
$$\begin{aligned} x = \bar{x}, y = \bar{y},\quad u=\bar{r}\bar{u},\quad \text {and}\quad \varepsilon =\bar{r}^{n-1}\bar{\varepsilon }; \end{aligned}$$
(20)

here, \(B=\mathbb {R}^2\times \mathbb {S}^1\times [0,r_0]\), where \((\bar{u},\bar{\varepsilon })\in \mathbb {S}^1\), with \(\mathbb {S}^1\) the unit circle, and \(r_0\) is positive and fixed. As the preimage of the hyperplane \(\{u=0\}\) under \(\Phi \) equals \(\mathbb {R}^2\times \mathbb {S}^1\times \{0\}\), \(\mathcal {S}\) is hence blown up to a cylinder in \(\mathbb {R}^4\); see Fig. 3 for a visualization.

We will require two coordinate charts in our analysis, which we denote by \(K_1\) and \(K_2\); these charts are obtained for \(\bar{u}=1\) and \(\bar{\varepsilon }=1\) in (20), respectively, which implies

$$\begin{aligned} \Phi _1:\ x=x_1,\quad y=y_1,\quad u=r_1,\quad \text {and}\quad \varepsilon =r_1^{n-1}\varepsilon _1 \end{aligned}$$
(21)

and

$$\begin{aligned} \Phi _2:\ x=x_2,\quad y=y_2,\quad u=r_2u_2,\quad \text {and}\quad \varepsilon =r_2^{n-1} \end{aligned}$$
(22)

for the blow-up transformation \(\Phi \) therein. Loosely speaking, the phase-directional chart \(K_1\) covers a neighborhood of the equator of the blow-up cylinder \(\mathbb {R}^2\times \mathbb {S}^1\times \{0\}\), while the top of that cylinder is covered by the rescaling chart \(K_2\); cf. again Fig. 3. The change-of-coordinates transformation \(\kappa _{12}\) between charts \(K_1\) and \(K_2\) is given by

$$\begin{aligned} \kappa _{12}: (x_1, y_1, r_1,\varepsilon _1)\mapsto \big (x_2,\, y_2,\,r_2u_2,\,u_2^{1-n}\big ); \end{aligned}$$
(23)

its inverse \(\kappa _{21}=\kappa _{12}^{-1}\) reads

$$\begin{aligned} \kappa _{21}: (x_2, y_2,u_2, r_2)\mapsto \Big (x_1,\, y_1,\,\varepsilon _1^{\frac{1}{1-n}},\,r_1\varepsilon _1^{\frac{1}{n-1}}\Big ). \end{aligned}$$
(24)

We define several sections for the flow of Eq. (11) – or, rather, of the corresponding blown-up systems in charts \(K_1\) and \(K_2\):

$$\begin{aligned} \Sigma _1^{\mathrm{in}}&:=\Big \{ (x_1,y_1,r_0,\varepsilon _1) \, \Big | \, \ x_1\in [-X,X],\nonumber \\&\quad y_1\in [-Y,Y],\text { and }\varepsilon _1\in [0,1]\, \Big \}, \end{aligned}$$
(25a)
$$\begin{aligned} \Sigma _1^{\mathrm{out}}&:=\Big \{ (x_1,y_1,r_1,1) \, \Big | \, \ x_1\in [-X,X],\nonumber \\&\quad y_1\in [-Y,Y],\text { and }r_1\in [0,r_0] \Big \}, \end{aligned}$$
(25b)
$$\begin{aligned} \Sigma _2^{\mathrm{in}}&:=\Big \{ (x_2,y_2,1,r_2) \, \Big | \, \ x_2\in [-X,X],\nonumber \\&\quad y_2\in [-Y,Y],\text { and }r_2\in \Big [0,\varepsilon _0^{\frac{1}{n-1}}\Big ] \Big \}. \end{aligned}$$
(25c)

Here, X and Y, as well as \(r_0\), are positive constants that are defined as before. The sections \(\Sigma _1^{\mathrm{in}}\) and \(\Sigma _1^{\mathrm{out}}\) clearly correspond to the respective boundaries between the inner region I and the intermediate region II and between the intermediate region II and the outer region III, respectively, when expressed in the original \((x,y,u,\varepsilon )\)-coordinates; recall Sect. 1. For future reference, we note that the section \(\Sigma _1^{\mathrm{in}}\) is equivalent to \(\Sigma ^{\mathrm{in}}\), after blow-up and transformation to chart \(K_1\), while \(\Sigma _1^{\mathrm{out}}\) corresponds to the section \(\Sigma _2^{\mathrm{in}}\) under the change of coordinates \(\kappa _{12}\) defined in (23): \(\Sigma _1^{\mathrm{out}}=\kappa _{12}(\Sigma _2^{\mathrm{in}})\).

We emphasize that \(K_1\) is the natural entry chart for the flow of Eq. (4) after blow-up due to \(u(=r_1)\) decaying monotonically to zero; recall Sect. 2.1, where “inner” expansions for the corresponding solutions were derived. Hence, any orbit of the associated blown-up vector field will intersect the section \(\Sigma _1^{\mathrm{in}}\) in finite time. As will become apparent below, orbits will enter chart \(K_2\) through \(\Sigma _2^{\mathrm{in}}\) after passage through \(K_1\); that step is the direct geometric analogue of asymptotic matching between the “outer” and “inner” solution expansions for (4). In particular, the asymptotics in the rescaling chart \(K_2\) will be regular in \(r_2\), and will correspond to the “outer” solution expansion.

Fig. 3
figure 3

Geometry of the blow-up transformation \(\Phi \) in Eq. (20). (For illustrative purposes, x and y are graphed on a single axis.)

Full size image

Remark 4

For any object \(\square \) in \((x,y,u,\varepsilon )\)-space, we denote the corresponding blown-up object by \(\overline{\square }\). Moreover, in chart \(K_{i}\) \((i=1,2)\), that object will be denoted by \(\square _{i}\).

Remark 5

The blow-up transformation defined in (20) is homogeneous in \(\bar{r}\). In general, one may make a quasi-homogeneous ansatz of the form \(x=\bar{r}^{\alpha _1}\bar{x}\), \(y=\bar{r}^{\alpha _2}\bar{y}\), \(u=\bar{r}^{\alpha _3}\bar{u}\), and \(\varepsilon =\bar{r}^{\alpha _4}\bar{\varepsilon }\), where \(\alpha _i\) \((i=1,\dots ,4)\) are positive integers; see e.g. [4]. One typically determines \(\alpha _i\) by finding a distinguished limit in the resulting rescaling chart, i.e., by balancing powers of \(\bar{r}\) there. An alternative, more systematic approach is produced by the method of Newton polygons [1].

3.1 Dynamics in region III

The dynamics in the “inner” region III is naturally described in the rescaling chart \(K_2\), where the blow-up transformation defined in (20) is expressed as in (22), corresponding to a rescaling of (x, y, u) in powers of \(\varepsilon \); substituting into Eq. (11), we find

$$\begin{aligned} x_2'&=r_2^{n-1}y_2, \end{aligned}$$
(26a)
$$\begin{aligned} y_2'&=r_2^{n-1}(r_2u_2-x_2), \end{aligned}$$
(26b)
$$\begin{aligned} u_2'&=-r_2^{n-1}u_2^n, \end{aligned}$$
(26c)
$$\begin{aligned} r_2'&=0 \end{aligned}$$
(26d)

in the coordinates of that chart.

By dividing out a factor of \(r_2^{n-1}\) from the right-hand sides in Eq. (26), we obtain the desingularized equations

$$\begin{aligned} x_2'&=y_2, \end{aligned}$$
(27a)
$$\begin{aligned} y_2'&=r_2u_2-x_2, \end{aligned}$$
(27b)
$$\begin{aligned} u_2'&=-u_2^n, \end{aligned}$$
(27c)
$$\begin{aligned} r_2'&=0, \end{aligned}$$
(27d)

where the prime now denotes differentiation with respect to a new rescaled time \(\tau _2\). Next, we define the line \(\ell _2^+=\big \{ (0,0,0,r_2) \, \big | \, r_2 \in [0,\varepsilon _0^{\frac{1}{n-1}} \big \}\); for \(r_2 = \varepsilon ^{\frac{1}{n-1}}\) positive and fixed, the associated point on \(\ell _2^+\) corresponds to the point \(Q_\varepsilon ^+\) before blow-up.

A direct calculation yields

Lemma 1

Any point on \(\ell _2^+\) is a non-hyperbolic steady state for Eq. (27), with eigenvalues \(\pm i\) and 0.

We remark that the degeneracy of \(\ell _2^+\) is immaterial to us, as the flow in chart \(K_2\) will not be affected thereby; rather, generic orbits of Eq. (27) will bypass \(\ell _2^+\) entirely, as follows.

For \(r_2 = 0 (=\varepsilon )\), the solution to (27) is given as in (9); hence, orbits reduce to concentric circles in the \((x_2,y_2)\)-plane, i.e., on \(\mathcal {S}_2\), in the singular limit. For \(u_2\) positive and \(r_2=0\), we observe a drift of that family with decreasing \(u_2\) as \(\tau _2\rightarrow \infty \). In fact, we can easily solve Eq. (27c) to find \(u_2(\tau _2)=\big [(n-1)(c+\tau _2)\big ]^{\frac{1}{1-n}}\), where c is a constant that is determined by matching—or, rather, “patching” —with the incoming orbit from chart \(K_1\), as \(\Sigma _2^{\mathrm{in}}=\kappa _{12}(\Sigma _1^{\mathrm{out}})\). Let \(\Gamma _2\) denote the segment of the singular orbit \(\Gamma \) that is located in chart \(K_2\), and label the point of intersection of that orbit with \(\Sigma _2^{\mathrm{in}}\) as \(P_2^{\mathrm{in}} :\ (x_2^{\mathrm{in}},y_2^{\mathrm{in}},1,0)\), which implies \(u_2^{\mathrm{in}}=1\) and

$$\begin{aligned} u_2(\tau _2)=[1+(n-1)\tau _2]^{\frac{1}{1-n}}; \end{aligned}$$
(28)

recall Eq. (10c).

In sum, \(\Gamma _2\) can be written as

$$\begin{aligned}&\Gamma _2:=\big \{ (x_2,y_2,u_2,0) \, \big | \, x_2=x_2(\tau _2), y_2\nonumber \\&\quad =y_2(\tau _2),\ \text {and}\ u_2(\tau _2)\ \text {for}\ \tau _2\in [0,\infty ) \big \}, \end{aligned}$$
(29)

where \(x_2(\tau _2)=x_2^{\mathrm{in}}\cos (\tau _2)+y_2^{\mathrm{in}}\sin (\tau _2)\) and \(y_2(\tau _2)=y_2^{\mathrm{in}}\cos (\tau _2)-x_2^{\mathrm{in}}\sin (\tau _2)\), by (9), and where \(u_2(\tau _2)\) is as given in (28).

The smooth persistence of \(\Gamma _2\) for \(r_2\) positive and sufficiently small then follows from regular perturbation theory: substituting \(u_2(\tau _2)\) into (27b) and taking \(r_2(\tau _2)\equiv r_2\) constant, we can solve for \(x_2(\tau _2,r_2)\) and \(y_2(\tau _2,r_2)\) as follows:

$$\begin{aligned}&x_2(\tau _2,r_2) =x_2^{\mathrm{in}}\cos (\tau _2)+y_2^{\mathrm{in}}\sin (\tau _2)\nonumber \\&\quad +r_2\int _{0}^{\tau _2}\sin (\tau _2-\sigma ) [1+(n-1)\sigma ]^{\frac{1}{1-n}}\,d\sigma , \end{aligned}$$
(30a)
$$\begin{aligned}&y_2(\tau _2,r_2) =y_2^{\mathrm{in}}\cos (\tau _2)-x_2^{\mathrm{in}}\sin (\tau _2)\nonumber \\&\quad +r_2\int _{0}^{\tau _2}\cos (\tau _2-\sigma ) [1+(n-1)\sigma ]^{\frac{1}{1-n}}\,d\sigma . \end{aligned}$$
(30b)

The orbit \(\Gamma _2\) hence perturbs in a smooth fashion, for \(r_2\in [0,r_0]\) and \(\tau _2\in [0,T_2]\), with \(T_2>0\) arbitrary, to an orbit \(\Gamma _{2\varepsilon }\) for Eq. (27) that is initiated in a point \(P_{2\varepsilon }^{\mathrm{in}}:\ \big (x_2^{\mathrm{in}},y_2^{\mathrm{in}},1,\varepsilon ^{\frac{1}{n-1}}\big )\in \Sigma _2^{\mathrm{in}}\).

Remark 6

Equation (30) can alternatively be obtained from Green’s function theory [3], as \(G(\tau _2,\sigma )=\sin (\tau _2-\sigma )\) is a Green’s function for the differential operator \(\frac{d^2}{d\tau _2^2}+1\). Alternatively still, one may make use of the fact that Eq. (27) is near-integrable to derive the asymptotics in (30); see, e.g., [8] for details and references.

The geometry in chart \(K_2\) is illustrated in Fig. 4.

Fig. 4
figure 4

Dynamics in chart \(K_2\): singular orbit \(\Gamma _2\) (blue) and perturbed orbit \(\Gamma _{2\varepsilon }\) (red). (Color figure online)

Full size image

3.2 Dynamics in region II

The dynamics in the “intermediate” region II is naturally described in chart \(K_1\), where the blow-up transformation defined in (20) is expressed as in (21); substituting into Eq. (11) and dividing out a factor of \(r_1^{n-1}\) from the resulting equations, we obtain

$$\begin{aligned} x_1'&=\varepsilon _1 y_1, \end{aligned}$$
(31a)
$$\begin{aligned} y_1'&=\varepsilon _1 (r_1-x_1), \end{aligned}$$
(31b)
$$\begin{aligned} r_1'&=-r_1, \end{aligned}$$
(31c)
$$\begin{aligned} \varepsilon _1'&=(n-1)\varepsilon _1, \end{aligned}$$
(31d)

where the prime denotes differentiation with respect to a new rescaled time \(\tau _1\).

The steady states of Eq. (31) are located in the plane

$$\begin{aligned}&\pi _1:=\big \{ (x_1,y_1 ,0,0) \, \big | \, x_1\in [-X,X]\text { and }\\&\quad y_1\in [-Y,Y] \big \}; \end{aligned}$$

here, X and Y are suitably chosen, positive constants, as before.

Linearization of (31) about \(\pi _1\) shows

Lemma 2

Any point in \(\pi _1\) is a partially hyperbolic steady state for Eq. (31), with eigenvalues \(-1\), 0 (double), and \(n-1\).

Blow-up has hence resulted in a partial desingularization of the flow of (11) in a neighborhood of \(\mathcal {S}_\varepsilon \), as we have gained two hyperbolic directions, by Lemma 2.

3.2.1 Singular limit

The singular limit of \(\varepsilon =0\) in (11) yields two limiting systems, which are obtained by setting \(r_1=0\) and \(\varepsilon _1=0\), respectively, in Eq. (31):

$$\begin{aligned} x_1'&=\varepsilon _1y_1, \end{aligned}$$
(32a)
$$\begin{aligned} y_1'&=-\varepsilon _1 x_1, \end{aligned}$$
(32b)
$$\begin{aligned} \varepsilon _1'&=(n-1)\varepsilon _1 \end{aligned}$$
(32c)

and

$$\begin{aligned} x_1'&=0, \end{aligned}$$
(33a)
$$\begin{aligned} y_1'&=0, \end{aligned}$$
(33b)
$$\begin{aligned} r_1'&=-r_1, \end{aligned}$$
(33c)

respectively. Let \(P_1^{\mathrm{in}}:\ (x_0,y_0,r_0,0)\), which corresponds to the point \(P^{\mathrm{in}}\) after blow-up and transformation to chart \(K_1\); recall Sect. 2.1. The segment of the singular orbit \(\Gamma \) in the invariant hyperplane \(\{\varepsilon _1=0\}\), which we label \(\Gamma _1^-\), will connect \(P_1^{\mathrm{in}}\) to a point \((x_0,y_0,0,0)\in \pi _1\), by (33):

$$\begin{aligned} \Gamma _1^-:=\big \{ (x_0,y_0,r_1,0) \, \big | \, r_1\in [0,r_0] \big \}. \end{aligned}$$
(34)

Here, we note that \(\Gamma _1^-\) corresponds to the leading-order inner solution, initiated in the point \(Q^-\), after transformation to chart \(K_1\): in particular, after blow-up, we thus observe exponential decay toward \(\{r_1=0\}\), i.e., to the equivalent of the critical manifold \(\mathcal {S}\) in \(K_1\).

Similarly, in the invariant hyperplane \(\{r_1=0\}\), we identify the segment of the singular orbit \(\Gamma \) which corresponds to the leading-order outer solution through the point \(Q_1=(x_0,y_0,0,0)\); we label that segment \(\Gamma _1^+\). To derive a representation for \(\Gamma _1^+\), we rewrite Eq. (32) by introducing \(\varepsilon _1\) as the independent variable:

$$\begin{aligned} \frac{dx_1}{d\varepsilon _1}&=\frac{ y_1}{n-1}, \end{aligned}$$
(35a)
$$\begin{aligned} \frac{dy_1}{d\varepsilon _1}&=-\frac{ x_1}{n-1}, \end{aligned}$$
(35b)

which can be solved explicitly with \(x_1(0)=x_0\) and \(y_1(0)=y_0\) to give

$$\begin{aligned} x_1(\varepsilon _1)&=x_0\cos \Big (\frac{\varepsilon _1}{n-1}\Big )+y_0\sin \Big (\frac{\varepsilon _1}{n-1}\Big ), \end{aligned}$$
(36a)
$$\begin{aligned} y_1(\varepsilon _1)&=y_0\cos \Big (\frac{\varepsilon _1}{n-1}\Big )-x_0\sin \Big (\frac{\varepsilon _1}{n-1}\Big ). \end{aligned}$$
(36b)

Hence, the orbit \(\Gamma _1^+\) can be expressed as

$$\begin{aligned}&\Gamma _1^+:=\big \{ (x_1,y_1,0,\varepsilon _1) \, \big | \, x_1=x_1(\varepsilon _1)\ \text {and}\ y_1\nonumber \\&\quad =y_1(\varepsilon _1)\ \text {for}\ \varepsilon _1\in [0,1] \big \}. \end{aligned}$$
(37)

In summary, the portion of \(\Gamma \) that lies in the intermediate region II consists of the union of the two orbits \(\Gamma _1^-\) and \(\Gamma _1^+\) and the steady state at \(Q_1\). The geometry in chart \(K_1\) is illustrated in Fig. 5.

Fig. 5
figure 5

Dynamics in chart \(K_1\): singular orbit \(\Gamma _1^\mp \) (blue) and perturbed orbit \(\Gamma _{1\varepsilon }\) (red). (Color figure online)

Full size image

3.2.2 Transition through region II

Next, we establish the persistence of the singular heteroclinic orbit \(\Gamma \) for \(\varepsilon \) positive and sufficiently small. To that end, we need to connect the two persistent orbits \(\Gamma _\varepsilon ^{\mathrm{I}}\) and \(\Gamma _{2\varepsilon }\), as constructed in Sects. 3.1 and 3.2, respectively, via the orbit segment \(\Gamma _{1\varepsilon }\) that is located in region II. Thus, we need to describe the transition between the sections \(\Sigma _1^{\mathrm{in}}\) and \(\Sigma _1^{\mathrm{out}}\) under the flow of (31); recall (25). Specifically, we will approximate the transition map \(\Pi _1\), with

$$\begin{aligned} \Pi _1:\ {\left\{ \begin{array}{ll} \Sigma _1^{\mathrm{in}}\rightarrow \Sigma _1^{\mathrm{out}}, \\ \big (x_1^{\mathrm{in}},y_1^{\mathrm{in}},r_0,r_0^{1-n}\varepsilon \big )\mapsto \Big (x_1^{\mathrm{out}},y_1^{\mathrm{out}},\varepsilon ^{\frac{1}{n-1}},1\Big ); \end{array}\right. } \end{aligned}$$
(38)

in other words, \(\Pi _1\) maps the point \(P_{1\varepsilon }^{\mathrm{in}}:=\Gamma _{1\varepsilon }\cap \Sigma _1^{\mathrm{in}}\) to the point \(P_{1\varepsilon }^{\mathrm{out}}:=\Gamma _{1\varepsilon }\cap \Sigma _1^{\mathrm{out}}\), where \(x_1^{\mathrm{in}}=x_0+\mathcal {O}(\varepsilon )\) and \(y_1^{\mathrm{in}}=y_0+\mathcal {O}(\varepsilon )\) are defined as in Eqs. (18) and (19) for \(n\ne 2\) and \(n=2\), respectively.

We will distinguish between the three cases of \(1<n<2\), \(n=2\), and \(n>2\) in Eq. (31), which we discuss in turn now. We begin by considering the case where \(1<n<2\).

Proposition 1

Let \(1<n<2\) in Eq. (31), and let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small. Then, there holds

$$\begin{aligned}&x_1^{\mathrm{out}} =x_0\cos \Big (\frac{1}{n-1}\Big )+y_0\sin \Big (\frac{1}{n-1}\Big )\nonumber \\&\quad -\varepsilon \bigg [\frac{y_0}{n-1}u_0^{1-n}\cos \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\frac{x_0}{n-1}u_0^{1-n}\sin \Big (\frac{1}{n-1}\Big )\nonumber \\&\quad +\frac{u_0^{2-n}}{n-2}\sin \Big (\frac{1}{n-1}\Big )\bigg ]\nonumber \\&\quad +\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big ), \end{aligned}$$
(39a)
$$\begin{aligned}&y_1^{\mathrm{out}} =y_0\cos \Big (\frac{1}{n-1}\Big )-x_0\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad +\varepsilon \bigg [\frac{x_0}{n-1}u_0^{1-n}\cos \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad +\frac{y_0}{n-1}u_0^{1-n}\sin \Big (\frac{1}{n-1}\Big )\nonumber \\&\quad -\frac{u_0^{2-n}}{n-2}\cos \Big (\frac{1}{n-1}\Big )\bigg ]\nonumber \\&\quad +\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big ), \end{aligned}$$
(39b)
$$\begin{aligned}&r_1^{\mathrm{out}} =\varepsilon ^{\frac{1}{n-1}} \end{aligned}$$
(39c)

in Eq. (38).

Proof

In a first step, we introduce \(\varepsilon _1\) as the independent variable in Eq. (31), which gives

$$\begin{aligned} \frac{dx_1}{d\varepsilon _1}&=\frac{1}{n-1}y_1, \end{aligned}$$
(40a)
$$\begin{aligned} \frac{dy_1}{d\varepsilon _1}&=\frac{1}{n-1}(r_1-x_1), \end{aligned}$$
(40b)
$$\begin{aligned} \frac{dr_1}{d\varepsilon _1}&=-\frac{1}{n-1}\frac{r_1}{\varepsilon _1}; \end{aligned}$$
(40c)

clearly, Eq. (40c) can be solved explicitly for \(r_1(\varepsilon _1)\), as it decouples from the \((x_1,y_1)\)-subsystem in (40): imposing \(r_1(r_0^{1-n}\varepsilon )=r_0\) in \(\Sigma _1^{\mathrm{in}}\), we find

$$\begin{aligned} r_1(\varepsilon _1)=\varepsilon ^{\frac{1}{n-1}}\varepsilon _1^{\frac{1}{1-n}}, \end{aligned}$$
(41)

which immediately implies (39c), as \(\varepsilon _1=1\) in \(\Sigma _1^{\mathrm{out}}\), by (25). In particular, the flow of (40) hence enters chart \(K_1\) through the section \(\Sigma _1^{\mathrm{in}}\), evolves with increasing \(\varepsilon _1\), and leaves via the section \(\Sigma _1^{\mathrm{out}}\).

Substituting (41) into (40), we can solve the resulting equations for \(x_1(\varepsilon _1)\) and \(y_1(\varepsilon _1)\), with initial condition \((x_1,y_1)\big |_{\{\varepsilon _1=r_0^{1-n}\varepsilon \}}=(x_1^{\mathrm{in}},y_1^{\mathrm{in}})\); thus, we find \(x_1(\varepsilon _1)=x_{1h}(\varepsilon _1)+x_{1p}(\varepsilon _1)\) and \(y_1(\varepsilon _1)=y_{1h}(\varepsilon _1)+y_{1p}(\varepsilon _1)\) for the solution to (40a) and (40b), where the homogeneous solution is given by

$$\begin{aligned}&\begin{aligned}&x_{1h}(\varepsilon _1) =\Big [x_1^{\mathrm{in}}\cos \Big (\frac{\varepsilon _1}{n-1}\Big )\\&\quad +y_1^{\mathrm{in}}\sin \Big (\frac{\varepsilon _1}{n-1}\Big )\Big ] \cos \Big (\frac{r_0^{1-n}\varepsilon }{n-1}\Big ) \\&\quad -\Big [y_1^{\mathrm{in}}\cos \Big (\frac{\varepsilon _1}{n-1}\Big )\\&\quad -x_1^{\mathrm{in}}\sin \Big (\frac{\varepsilon _1}{n-1}\Big )\Big ] \sin \Big (\frac{r_0^{1-n}\varepsilon }{n-1}\Big ), \end{aligned} \end{aligned}$$
(42a)
$$\begin{aligned}&\begin{aligned}&y_{1h}(\varepsilon _1) =\Big [y_1^{\mathrm{in}}\cos \Big (\frac{\varepsilon _1}{n-1}\Big )\\&\quad -x_1^{\mathrm{in}}\sin \Big (\frac{\varepsilon _1}{n-1}\Big )\Big ] \cos \Big (\frac{r_0^{1-n}\varepsilon }{n-1}\Big ) \\&\quad +\Big [x_1^{\mathrm{in}}\cos \Big (\frac{\varepsilon _1}{n-1}\Big )\\&\quad +y_1^{\mathrm{in}}\sin \Big (\frac{\varepsilon _1}{n-1}\Big )\Big ] \sin \Big (\frac{r_0^{1-n}\varepsilon }{n-1}\Big ). \end{aligned} \end{aligned}$$
(42b)

We first assume that \(n\ne \frac{k+1}{k}\), with \(k=2,3,\dots \) integer; then, the particular solution reads

$$\begin{aligned}&\begin{aligned}&x_{1p}(\varepsilon _1) =-\frac{1}{(n-1)(2n-3)}\\&\quad \Big [\varepsilon ^{\frac{1}{n-1}}\varepsilon _1^{\frac{2n-3}{n-1}} \, _{1}F_2\Big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{\varepsilon _1^2}{4(n-1)^2}\Big )\\&\quad -r_0^{3-2n}\varepsilon ^2\, _{1}F_2\Big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{r_0^{2-2n}\varepsilon ^2}{4(n-1)^2}\Big )\Big ]\\&\quad \times \cos \Big (\frac{\varepsilon _1}{n-1}\Big ) \\&\quad +\frac{1}{n-2}\Big [\varepsilon ^{\frac{1}{n-1}}\varepsilon _1^{\frac{n-2}{n-1}} \, _{1}F_2\Big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{\varepsilon _1^2}{4(n-1)^2}\Big ) \\&\quad -r_0^{2-n}\varepsilon \, _{1}F_2\Big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{r_0^{2-2n}\varepsilon ^2}{4(n-1)^2}\Big )\Big ]\\&\quad \times \sin \Big (\frac{\varepsilon _1}{n-1}\Big ), \end{aligned} \end{aligned}$$
(43a)
$$\begin{aligned}&\begin{aligned}&y_{1p}(\varepsilon _1) =\frac{1}{n-2}\\&\quad \Big [\varepsilon ^{\frac{1}{n-1}}\varepsilon _1^{\frac{n-2}{n-1}} \, _{1}F_2\Big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{\varepsilon _1^2}{4(n-1)^2}\Big )\\&\quad -r_0^{2-n}\varepsilon \, _{1}F_2\Big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{r_0^{2-2n}\varepsilon ^2}{4(n-1)^2}\Big )\Big ]\\&\quad \times \cos \Big (\frac{\varepsilon _1}{n-1}\Big ) \\&\quad +\frac{1}{(n-1)(2n-3)}\\&\quad \Big [\varepsilon ^{\frac{1}{n-1}}\varepsilon _1^{\frac{2n-3}{n-1}} \,_{1}F_2\Big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{\varepsilon _1^2}{4(n-1)^2}\Big ) \\&\quad -r_0^{3-2n}\varepsilon ^2\, _{1}F_2\Big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{r_0^{2-2n}\varepsilon ^2}{4(n-1)^2}\Big )\Big ]\\&\quad \times \sin \Big (\frac{\varepsilon _1}{n-1}\Big ), \end{aligned} \end{aligned}$$
(43b)

where \(_{1}F_2\) denotes the generalized hypergeometric function [2, Chapter 16].

Given the definition of \(\Pi _1\) in Eq. (38), we need to evaluate (42) and (43) in \(\Sigma _1^{\mathrm{out}}\), i.e., for \(\varepsilon _1=1\), to obtain the sought-after asymptotics of \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\), as stated in (39). We only outline the argument for \(x_1^{\mathrm{out}}\) here, leaving the approximation of \(y_1^{\mathrm{out}}\) to the reader: expanding the contribution to \(x_1(1)\) from the homogeneous solution \(x_{1h}\) in (42a) and recalling the expansions for \(x_1^{\mathrm{in}}\) and \(y_1^{\mathrm{in}}\) from (18), we find

$$\begin{aligned}&x_{1h}(1)=x_0\cos \Big (\frac{1}{n-1}\Big )+y_0\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\varepsilon \bigg [\frac{y_0}{n-1}u_0^{1-n}\cos \Big (\frac{1}{n-1}\Big )\nonumber \\&\quad -\frac{x_0}{n-1}u_0^{1-n}\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\frac{r_0^{2-n}-u_0^{2-n}}{n-2}\sin \Big (\frac{1}{n-1}\Big )\bigg ]+\mathcal {O}(\varepsilon ^2). \end{aligned}$$
(44)

It remains to estimate the particular solution in (43a); to that end, we expand

$$\begin{aligned}&x_{1p}(1)=-\varepsilon \frac{r_0^{2-n}}{n-2}\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\varepsilon ^{\frac{1}{n-1}}\bigg [\frac{1}{(n-1)(2n-3)}\, _{1}F_2\big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};\nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big ) \cos \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\frac{1}{n-2}\, _{1}F_2\big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};\nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big ) \sin \Big (\frac{1}{n-1}\Big )\bigg ]+\mathcal {O}(\varepsilon ^2). \end{aligned}$$
(45)

Since, however, \(1<n<2\) implies that \(\mathcal {O}(\varepsilon ^{\frac{1}{n-1}})={\scriptstyle \mathcal {O}}(\varepsilon )\), only the first term in (45) contributes to the order considered here. Combining Eqs. (44) and (45), we hence obtain Eq. (39a), as claimed; we note that the error is \(\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big )\) due to the fact that \(2<\frac{1}{n-1}\) for \(1<n<\frac{3}{2}\), whereas the reverse is true for \(\frac{3}{2}<n<2\). Moreover, we remark that (39a) is \(r_0\)-independent, as is to be expected.

Finally, the case where \(n=\frac{k+1}{k}\) in (40) has to be studied separately, as was also done in [14], since the hypergeometric functions occurring in (43) are not defined then. It can be shown that the particular solutions \(x_{1p}(\varepsilon _1)\) and \(y_{1p}(\varepsilon _1)\) can be expressed in terms of the Sine Integral and the Cosine Integral [2, Chapter 6] in that case, with

$$\begin{aligned} \mathrm{Si}(x)&=\int _0^x\frac{\sin (s)}{s}\,ds\quad \text {and}\quad \mathrm{Ci}(x)\\&=-\int _x^\infty \frac{\cos (s)}{s}\,ds. \end{aligned}$$

Since the corresponding expressions are algebraically involved, we do not reproduce them; however, a straightforward adaptation of the above argument show that the resulting asymptotics of \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) is again given by Eq. (39) to the order considered here, which completes the proof. \(\square \)

Remark 7

Equation (40) can equally be solved by combining (40a) and (40b) into the second-order equation

$$\begin{aligned} \frac{d^2x_1}{d\varepsilon _1^2}+\frac{1}{(n-1)^2}x_1=\frac{\varepsilon ^{\frac{1}{n-1}} \varepsilon _1^{\frac{1}{1-n}}}{(n-1)^2}; \end{aligned}$$

the Green’s function for the above differential operator is given by \(G(s)=(n-1)\sin \big (\frac{s}{n-1}\big )\), which implies the particular solution

$$\begin{aligned} \frac{\varepsilon ^{\frac{1}{n-1}}}{n-1}\int _{r_0^{1-n}\varepsilon }^{\varepsilon _1}\sin \Big (\frac{\varepsilon _1-s}{n-1} \Big )s^{\frac{1}{1-n}}ds. \end{aligned}$$

Expanding that integral, as well as the corresponding homogeneous solution, in \(\varepsilon _1\) and evaluating the result in \(\Sigma _1^{\mathrm{out}}\), one may then again approximate \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) as above.

Next, we consider the borderline case of \(n=2\); in particular, we prove the occurrence of logarithmic “switchback” terms (in \(\varepsilon \)) in the resulting asymptotics:

Proposition 2

Let \(n=2\) in Eq. (31), and let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small. Then, there holds

$$\begin{aligned} x_1^{\mathrm{out}}&=x_0\cos (1)+y_0\sin (1)-\sin (1)\varepsilon \ln \varepsilon +\mathcal {O}(\varepsilon ), \end{aligned}$$
(46a)
$$\begin{aligned} y_1^{\mathrm{out}}&=y_0\cos (1)-x_0\sin (1)-\cos (1)\varepsilon \ln \varepsilon +\mathcal {O}(\varepsilon ), \end{aligned}$$
(46b)
$$\begin{aligned} r_1^{\mathrm{out}}&=\varepsilon . \end{aligned}$$
(46c)

Proof

For \(n=2\), Eq. (40c) admits the solution \(r_1(\varepsilon _1)=\frac{\varepsilon }{\varepsilon _1}\); substituting into (40a) and (40b) and solving, we find the following expressions for \(x_1(\varepsilon _1)=x_{1h}(\varepsilon _1)+x_{1p}(\varepsilon _1)\) and \(y_1(\varepsilon _1)=y_{1h}(\varepsilon _1)+y_{1p}(\varepsilon _1)\):

$$\begin{aligned}&x_{1h}(\varepsilon _1) =\big [x_1^{\mathrm{in}}\cos (\varepsilon _1)+y_1^{\mathrm{in}}\sin (\varepsilon _1)\big ]\cos \Big (\frac{\varepsilon }{r_0}\Big )\nonumber \\&\quad -\big [y_1^{\mathrm{in}}\cos (\varepsilon _1)-x_1^{\mathrm{in}}\sin (\varepsilon _1)\big ]\sin \Big (\frac{\varepsilon }{r_0}\Big ), \end{aligned}$$
(47a)
$$\begin{aligned}&x_{1p}(\varepsilon _1) =\varepsilon \Big [\mathrm{Si}\Big (\frac{\varepsilon }{r_0}\Big )-\mathrm{Si}(\varepsilon _1)\Big ]\cos (\varepsilon _1)\nonumber \\&\quad -\varepsilon \Big [\mathrm{Ci}\Big (\frac{\varepsilon }{r_0}\Big )-\mathrm{Ci}(\varepsilon _1)\Big ]\sin (\varepsilon _1), \end{aligned}$$
(47b)
$$\begin{aligned}&y_{1h}(\varepsilon _1) =\big [y_1^{\mathrm{in}}\cos (\varepsilon _1)-x_1^{\mathrm{in}}\sin (\varepsilon _1)\big ]\cos \Big (\frac{\varepsilon }{r_0}\Big )\nonumber \\&\quad +\big [x_1^{\mathrm{in}}\cos (\varepsilon _1)+y_1^{\mathrm{in}}\sin (\varepsilon _1)\big ]\sin \Big (\frac{\varepsilon }{r_0}\Big ), \end{aligned}$$
(47c)
$$\begin{aligned}&y_{1p}(\varepsilon _1) =-\varepsilon \Big [\mathrm{Ci}\Big (\frac{\varepsilon }{r_0}\Big )-\mathrm{Ci}(\varepsilon _1)\Big ]\cos (\varepsilon _1)\nonumber \\&\quad -\varepsilon \Big [\mathrm{Si}\Big (\frac{\varepsilon }{r_0}\Big )-\mathrm{Si}(\varepsilon _1)\Big ]\sin (\varepsilon _1) \end{aligned}$$
(47d)

for the solution to (40) with initial condition \((x_1,y_1)\big |_{\{\varepsilon _1=r_0^{-1}\varepsilon \}}=(x_1^{\mathrm{in}},y_1^{\mathrm{in}})\). Here, \(\mathrm{Si}\) and \(\mathrm{Ci}\) denote the Sine Integral and the Cosine Integral, respectively, as before; in particular, we have the expansions

$$\begin{aligned} \mathrm{Si}(x)&=\sum _{k=1}^\infty (-1)^{k-1}\frac{x^{2k-1}}{(2k-1)(2k-1)!}\\&=x-\frac{1}{18}x^3+\mathcal {O}(x^5)\quad \text {and} \\ \mathrm{Ci}(x)&=\gamma +\ln x+\sum _{k=1}^\infty (-1)^k\frac{x^{2k}}{2k(2k)!}\\&=\gamma +\ln x-\frac{1}{4}x^2+\mathcal {O}(x^4) \end{aligned}$$

at \(x=0\), where \(\gamma =\lim _{n\rightarrow \infty }\big (-\ln n+\sum _{k=1}^n\frac{1}{k}\big )\) denotes the Euler-Mascheroni constant [2, Chapter 6]. Substituting for \(x_1^{\mathrm{in}}\) and \(y_1^{\mathrm{in}}\) from (19) in (47), evaluating the result at \(\varepsilon _1=1\), and expanding in \(\varepsilon \), we obtain the expansion for \(x_1^{\mathrm{out}}\) in (46a), as claimed. The derivation of (46b) is analogous. \(\square \)

Finally, we consider the case of \(n>2\).

Proposition 3

Let \(n>2\) in Eq. (31), and let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small. Then, there holds

$$\begin{aligned}&x_1^{\mathrm{out}} =x_0\cos \Big (\frac{1}{n-1}\Big )+y_0\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\varepsilon ^{\frac{1}{n-1}}\bigg [\frac{1}{(n-1)(2n-3)}\, _{1}F_2\big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};\nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big ) \cos \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad -\frac{1}{n-2}\, _{1}F_2\big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};\nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big ) \sin \Big (\frac{1}{n-1}\Big )\bigg ] +\mathcal {O}(\varepsilon ), \end{aligned}$$
(48a)
$$\begin{aligned}&y_1^{\mathrm{out}} =y_0\cos \Big (\frac{1}{n-1}\Big )-x_0\sin \Big (\frac{1}{n-1}\Big ) \nonumber \\&\quad +\varepsilon ^{\frac{1}{n-1}}\bigg [\frac{1}{n-2} \, _{1}F_2\big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};\nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big )\cos \Big (\frac{1}{n-1}\Big )\nonumber \\&\qquad +\frac{1}{(n-1)(2n-3)}\, _{1}F_2\big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2}; \nonumber \\&\quad -\tfrac{1}{4(n-1)^2}\big ) \sin \Big (\frac{1}{n-1}\Big )\bigg ] +\mathcal {O}(\varepsilon ), \end{aligned}$$
(48b)
$$\begin{aligned}&r_1^{\mathrm{out}} =\varepsilon ^{\frac{1}{n-1}} \end{aligned}$$
(48c)

in Eq. (38); here, \(_{1}F_2\) again denotes the generalized hypergeometric function.

Proof

The proof is similar to that of Proposition 1; in particular, the closed-form solution in (42) is still valid when \(n>2\). As was done there, we evaluate that solution at \(\varepsilon _1=1\), i.e., in \(\Sigma _1^{\mathrm{out}}\). Again, we only outline the argument for \(x_1^{\mathrm{out}}\) here, leaving the approximation of \(y_1^{\mathrm{out}}\) to the reader: the contribution to \(x_1^{\mathrm{out}}\) from the homogeneous and particular solutions is given by (44) and (45), respectively, as before; however, since \(n>2\) now, it follows that the \(\mathcal {O}(\varepsilon )\)-correction therein is \({\scriptstyle \mathcal {O}}(\varepsilon ^{\frac{1}{n-1}})\) due to \(\frac{1}{n-1}>1\). Hence, only the \(\mathcal {O}(\varepsilon ^{\frac{1}{n-1}})\)-term in (45) contributes to \(x_1^{\mathrm{out}}\) to the order considered here, which implies Eq. (48a), as claimed. (A similar observation was made in Sect. 5 of [14].) \(\square \)

The transition through chart \(K_1\) is the geometric analogue of the matching procedure performed by Verhulst in [14]; correspondingly, the occurrence of logarithmic (“switchback”) terms in the resulting asymptotic expansions for \(n=2\) was observed there already. From a geometric point of view, these terms can be shown to be due to resonances between the eigenvalues of the linearization of Eq. (31) about \(\pi _1\); recall Lemma 2. To motivate that observation, we note that the term \(r_1\varepsilon _1(=\varepsilon )\) in (31b) is resonant of order 2. We can then perform a sequence of near-identity normal form transformations in Eq. (31) in order to remove any non-resonant terms therefrom, which yields an approximation for the transition map \(\Pi _1\); see [16] for details.

Lemma 3

Let \(n=2\); then, there exists a sequence of near-identity transformations, with \((x_1,y_1)\mapsto (\xi ,\eta )\), such that Eq. (31) can be written as

$$\begin{aligned} \xi '&=\mathcal {O}(3), \end{aligned}$$
(49a)
$$\begin{aligned} \eta '&=\varepsilon +\mathcal {O}(3), \end{aligned}$$
(49b)
$$\begin{aligned} r_1'&=-r_1, \end{aligned}$$
(49c)
$$\begin{aligned} \varepsilon _1'&=\varepsilon _1. \end{aligned}$$
(49d)

Solving Eq. (3) with a transformed initial condition \((\xi ^{\mathrm{in}},\eta ^{\mathrm{in}},r_0,r_0^{-1}\varepsilon )\), we find

$$\begin{aligned} (\xi ,\eta ,r_1,\varepsilon _1)(\tau _1)=\big (\xi ^{\mathrm{in}},\eta ^{\mathrm{in}}+\varepsilon \tau _1,r_0\mathrm e^{-\tau _1},r_0^{-1}\varepsilon \mathrm e^{\tau _1}\big ) \end{aligned}$$
(50)

to the order considered here. Now, the transition time \(T_1\) between the (transformed) sections \(\Sigma _1^{\mathrm{in}}\) and \(\Sigma _1^{\mathrm{out}}\) can be determined by solving \(1=\varepsilon _1(T_1)=\frac{\varepsilon }{r_0}\mathrm e^{T_1}\), cf. Eq. (38), which gives \(T_1=-\ln \varepsilon +\mathcal {O}(1)\). Thus, \(\eta (T_1)=\eta _0-\varepsilon \ln \varepsilon +\mathcal {O}(\varepsilon )\) contains a logarithmic switchback term of the order \(\mathcal {O}(\varepsilon \ln \varepsilon )\), in agreement with Proposition 2 above.

Remark 8

Incidentally, logarithmic terms of the order \(\mathcal {O}(\varepsilon ^k\ln \varepsilon )\) are also found in the asymptotics resulting for \(n=\frac{k+1}{k}\), with \(k=2,3,4,\dots \), in the statement of Proposition 1; for \(k=2\), for instance, we have

$$\begin{aligned}&x_1 (\varepsilon _1)=\big [x_1^{\mathrm{in}}\cos (2\varepsilon _1)+y_1^{\mathrm{in}}\sin (2\varepsilon _1)\big ]\cos \big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )\\&\quad -\big [y_1^{\mathrm{in}}\cos (2\varepsilon _1)-x_1^{\mathrm{in}}\sin (2\varepsilon _1)\big ]\sin \big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big ) \\&\quad +2\sqrt{r_0}\varepsilon \sin \big (2\varepsilon \big (\tfrac{1}{\sqrt{r_1}}-\tfrac{1}{\sqrt{r_0}}\big )\big )+4\varepsilon ^2\big [\mathrm{Ci}\big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )\\&\quad -\mathrm{Ci}(2\varepsilon _1)\big ]+4\varepsilon ^2\big [\mathrm{Si}\big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )-\mathrm{Si}(2\varepsilon _1)\big ], \\&y_1 (\varepsilon _1)=\big [y_1^{\mathrm{in}}\cos (2\varepsilon _1)-x_1^{\mathrm{in}}\sin (2\varepsilon _1)\big ]\cos \big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )\\&\quad +\big [x_1^{\mathrm{in}}\cos (2\varepsilon _1)+y_1^{\mathrm{in}}\sin (2\varepsilon _1)\big ]\sin \big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big ) \\&\quad +2\sqrt{r_0}\varepsilon \cos \big (2\varepsilon \big (\tfrac{1}{\sqrt{r_1}}-\tfrac{1}{\sqrt{r_0}}\big )\big )+4\varepsilon ^2\big [\mathrm{Si}\big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )\\&\quad -\mathrm{Si}(2\varepsilon _1)\big ]-4\varepsilon ^2\big [\mathrm{Ci}\big (\tfrac{2\varepsilon }{\sqrt{r_0}}\big )-\mathrm{Ci}(2\varepsilon _1)\big ]-\frac{1}{2\varepsilon _1}. \end{aligned}$$

Evaluating the above at \(\varepsilon _1=1\), i.e., in \(\Sigma _1^{\mathrm{out}}\), and expanding the result in \(\varepsilon \), we find that the asymptotics of \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) contain the switchback terms \(4\cos (2)\varepsilon ^2\ln \varepsilon \) and \(-4\sin (2)\varepsilon ^2\ln \varepsilon \), respectively. These terms can be shown to be due to resonances at higher order in the governing equations in chart \(K_1\) via a higher-order normal transformation that specifies the \(\mathcal {O}(3)\)-terms in Eq. (3).

3.3 Summary

To summarize, the singular heteroclinic orbit \(\Gamma \) that connects the initial point \(Q^-\) to the critical manifold \(\mathcal {S}\)—or, rather, its analogue \(\bar{\Gamma }\) in the blow-up space—is defined as the union of the orbits \(\Gamma ^I\), \(\Gamma _1^-\), \(\Gamma _1^+\), and \(\Gamma _2\) obtained in Sects. 2.1, 3.1, and 3.2, respectively, as well as of the steady state at \(Q_1\). Similarly, for \(\varepsilon \) positive and sufficiently small, the orbit \(\bar{\Gamma }_{\bar{\varepsilon }}\) is obtained as the union of the corresponding persistent orbits \(\Gamma _\varepsilon ^I\), \(\Gamma _{1\varepsilon }\), and \(\Gamma _{2\varepsilon }\). The global geometry in the blow-up space is illustrated in Fig.  6.

Fig. 6
figure 6

Global geometry in the blow-up space: singular orbit \(\bar{\Gamma }\) (blue) and perturbed orbit \(\bar{\Gamma }_{\bar{\varepsilon }}\) (red). (Color figure online)

Full size image

4 Asymptotic expansions

Finally, we derive asymptotic solution expansions for Eq. (4) in regions I, II, and III; to that end, we recall that any orbit of (4) will terminate in the rescaling chart \(K_2\) (region III) after passage through chart \(K_1\) (region II) and the inner region I. It follows, in particular, that an expansion for \((x,y,u)(t,\varepsilon )\) which is valid for sufficiently large times t can be derived by tracking a given orbit \(\Gamma _\varepsilon \) that is initiated in region I through region II and into region III. (Correspondingly, the solution to the governing equations in \(K_2\), as given in Eq. (30), is bounded for \(\tau _2\rightarrow \infty \).) We denote by \(\Gamma _\varepsilon ^{\mathrm{II}}\) and \(\Gamma _\varepsilon ^{\mathrm{III}}\) the orbits that are obtained from \(\Gamma _{1\varepsilon }\) and \(\Gamma _{2\varepsilon }\), respectively, after blow-down, i.e., in the original \((x,y,u,\varepsilon )\)-space.

In a first step, we determine the value of the time variable \(\tau \) in the section \(\Sigma ^{\mathrm{out}}\), which is obtained from \(\Sigma _1^{\mathrm{out}}\)—or, equivalently, from \(\Sigma _2^{\mathrm{in}}\)—after blow-down; that section is defined as \(\big \{u=\varepsilon ^{\frac{1}{n-1}}\big \}\), by (22).

Lemma 4

Let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small, and let \(\tau ^{\mathrm{out}}\) be defined by \(u(\tau ^{\mathrm{out}})=\varepsilon ^{\frac{1}{n-1}}\) in \(\Sigma ^{\mathrm{out}}\); then,

$$\begin{aligned} \tau ^{\mathrm{out}}=\frac{1}{n-1}\Big (\frac{1}{\varepsilon }-u_0^{1-n}\Big ). \end{aligned}$$
(51)

Proof

Recalling the exact solution for \(u(\tau )\) from Eq. (10c), we solve \(u(\tau ^{\mathrm{out}})=\varepsilon ^{\frac{1}{n-1}}\) for \(\tau ^{\mathrm{out}}\) to obtain (51), as claimed. \(\square \)

As before, we consider separately the cases where \(1<n<2\), \(n=2\), and \(n>2\) in Eq. (4); moreover, we restrict to \(f(t,x,y,\varepsilon )\equiv 1\) throughout.

Proposition 4

Let \(1<n<2\) in Eq. (4), let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small, and let \(t\ge T>0\), with T sufficiently large. Then, the solution \((x,y,u)(t,\varepsilon )\) to (4) satisfies

$$\begin{aligned} x(t,\varepsilon )&=x_0\cos (t)+\Big (y_0-\varepsilon \frac{u_0^{2-n}}{n-2}\Big )\sin (t)\nonumber \\&\quad +\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big ), \end{aligned}$$
(52a)
$$\begin{aligned} y(t,\varepsilon )&=\Big (y_0-\varepsilon \frac{u_0^{2-n}}{n-2}\Big )\cos (t)-x_0\sin (t)\nonumber \\&\quad +\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big ), \end{aligned}$$
(52b)
$$\begin{aligned} u(t,\varepsilon )&=\varepsilon ^{\frac{1}{n-1}}[(n-1)t]^{\frac{1}{1-n}}+\mathcal {O}\big (\varepsilon ^{\frac{n}{n-1}}\big ), \end{aligned}$$
(52c)

where \(x_0\), \(y_0\), and \(u_0\) are defined as in Eq. (2).

Proof

We recall the expressions for \(x_2(\tau _2,r_2)\) and \(y_2(\tau _2,r_2)\) from Eq. (30); moreover, we observe that \(x_2\equiv x\), \(y_2\equiv y\), and \(r_2=\varepsilon ^{\frac{1}{n-1}}\), as well as that \(x_2^{\mathrm{in}}\equiv x_1^{\mathrm{out}}\) and \(y_2^{\mathrm{in}}\equiv y_1^{\mathrm{out}}\). Finally, we note that the transformation from \(\tau \) to \(\tau _2\) in \(K_2\) is defined through \(r_2^{n-1}\frac{d}{d\tau _2}=\frac{d}{d\tau }\), which implies \(\tau (\tau _2)-\tau ^{\mathrm{out}}=r_2^{1-n}\tau _2=\frac{\tau _2}{\varepsilon }\), by Eq. (22). Hence, it follows from Lemma 4 that

$$\begin{aligned} \tau (\tau _2)&=\frac{1}{n-1}\Big (\frac{1}{\varepsilon }-u_0^{1-n}\Big )+\frac{\tau _2}{\varepsilon }\quad \text {or}\\ \tau _2&=t-\frac{1}{n-1}\big (1-\varepsilon u_0^{1-n}\big ), \end{aligned}$$

where we recall that \(t=\varepsilon \tau \) denotes the slow time. Substituting the above into (30), i.e., integrating in t now, we find

$$\begin{aligned}&x(t,\varepsilon ) =x_1^{\mathrm{out}}\cos \Big (t-\frac{1}{n-1}+\varepsilon \frac{u_0^{1-n}}{n-1}\Big ) \nonumber \\&\quad +y_1^{\mathrm{out}}\sin \Big (t-\frac{1}{n-1}+\varepsilon \frac{u_0^{1-n}}{n-1}\Big ) \nonumber \\&\quad +\varepsilon ^{\frac{1}{n-1}}\int _{\frac{1}{n-1}(1-\varepsilon u_0^{1-n})}^t\sin (t-s)\big [(n-1)s\nonumber \\&\quad +\varepsilon u_0^{1-n}\big ]^{\frac{1}{1-n}}ds, \end{aligned}$$
(53a)
$$\begin{aligned}&y(t,\varepsilon ) =y_1^{\mathrm{out}}\cos \Big (t-\frac{1}{n-1}+\varepsilon \frac{u_0^{1-n}}{n-1}\Big )\nonumber \\&\quad -x_1^{\mathrm{out}}\sin \Big (t-\frac{1}{n-1}+\varepsilon \frac{u_0^{1-n}}{n-1}\Big ) \nonumber \\&\quad +\varepsilon ^{\frac{1}{n-1}}\int _{\frac{1}{n-1}(1-\varepsilon u_0^{1-n})}^t\cos (t-s)\big [(n-1)s\nonumber \\&\quad +\varepsilon u_0^{1-n}\big ]^{\frac{1}{1-n}}ds. \end{aligned}$$
(53b)

Making use of the expansions for \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) from (39), expanding the resulting expressions to first order in \(\varepsilon \), and applying the trigonometric identities \(\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )\) and \(\cos (\alpha +\beta )=\cos (\alpha )\cos (\beta )-\sin (\alpha )\sin (\beta )\), we find Eqs. (52a) and (52b), as claimed. Here, we note that the particular solution in (53) only contributes a correction of the order \(\mathcal {O}(\varepsilon ^{\frac{1}{n-1}})\), which is \({\scriptstyle \mathcal {O}}(\varepsilon )\) for \(1<n<2\), as well as that the overall error is \(\mathcal {O}\big (\varepsilon ^{\min \{2,\frac{1}{n-1}\}}\big )\), as in (39).

Finally, to show Eq. (52c), we rewrite (28) in terms of t to find \(u_2(t)=\big [(n-1)t+\varepsilon u_0^{1-n}\big ]^{\frac{1}{1-n}}\), which is consistent with the particular solution in (53); expanding \(u_2(t)\) in \(\varepsilon \), we obtain (52c), as claimed. \(\square \)

Remark 9

The expansions in Eq. (52) agree with the leading-order asymptotics from Sect. 5 of [14]; cf. in particular Eqs. (20) through (22).

Proposition 5

Let \(n=2\) in Eq. (4), let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small, and let \(t\ge T>0\), with T sufficiently large. Then, the solution \((x,y,u)(t,\varepsilon )\) to (4) satisfies

$$\begin{aligned} x(t,\varepsilon )&=x_0\cos (t)+(y_0-\varepsilon \ln \varepsilon )\sin (t)+\mathcal {O}(\varepsilon ), \end{aligned}$$
(54a)
$$\begin{aligned} y(t,\varepsilon )&= (y_0-\varepsilon \ln \varepsilon )\cos (t)-x_0\sin (t)+\mathcal {O}(\varepsilon ), \end{aligned}$$
(54b)
$$\begin{aligned} u(t,\varepsilon )&=\frac{\varepsilon }{t}+\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(54c)

where \(x_0\) and \(y_0\) are defined as in Eq. (2).

Proof

The proof is analogous to that of Proposition 4: substituting the expansions for \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) from (46) into Eq. (53), applying the same trigonometric identities as there, and noting that the particular solution in (53) contributes an \(\mathcal {O}(\varepsilon )\)-correction, we obtain (5). \(\square \)

Remark 10

The expansion in (5) can also be derived via a Green’s function approach: rewriting Eqs. (27a) and (27b) as a second-order equation and making use of (28), we find \(x_2''+x_2=\frac{r_2}{t+1}\), which has the particular solution

$$\begin{aligned}&r_2\int _0^t\frac{\sin (t-s)}{1+s}\,ds=-[\mathrm{Si}(t+1)-\mathrm{Si}(1)]\cos (t+1)\\&\quad +[\mathrm{Ci}(t+1)-\mathrm{Ci}(1)]\sin (t+1). \end{aligned}$$

(Here, \(\mathrm{Si}\) and \(\mathrm{Ci}\) denote the Sine Integral and the Cosine Integral, respectively, as before.)

Proposition 6

Let \(n>2\) in Eq. (4), let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small, and let \(t\ge T>0\), with T sufficiently large. Then, the solution \((x,y,u)(t,\varepsilon )\) to (4) satisfies

$$\begin{aligned}&\begin{aligned}&x(t,\varepsilon ) =\bigg \{x_0-\varepsilon ^{\frac{1}{n-1}}\frac{n-1}{2n-3}t^2[(n-1)t]^{\frac{1}{1-n}}\,\\&\quad _1F_2\big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{t^2}{4}\big )\bigg \}\cos (t) \\&\quad +\bigg \{y_0+\varepsilon ^{\frac{1}{n-1}}\frac{n-1}{n-2}t[(n-1)t]^{\frac{1}{1-n}}\\&\quad _1F_2\big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{t^2}{4}\big )\bigg \}\sin (t)+\mathcal {O}(\varepsilon ), \end{aligned} \end{aligned}$$
(55a)
$$\begin{aligned}&\begin{aligned}&y(t,\varepsilon ) =\bigg \{y_0+\varepsilon ^{\frac{1}{n-1}}\frac{n-1}{n-2}t[(n-1)t]^{\frac{1}{1-n}}\\&\quad _1F_2\big (\tfrac{n-2}{2n-2},\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{t^2}{4}\big )\bigg \}\cos (t) \\&\quad -\bigg \{x_0-\varepsilon ^{\frac{1}{n-1}}\frac{n-1}{2n-3}t^2[(n-1)t]^{\frac{1}{1-n}}\\&\quad _1F_2\big (\tfrac{2n-3}{2n-2},\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{t^2}{4}\big )\bigg \}\sin (t)+\mathcal {O}(\varepsilon ), \end{aligned} \end{aligned}$$
(55b)
$$\begin{aligned}&u(t,\varepsilon ) =\varepsilon ^{\frac{1}{n-1}}[(n-1)t]^{\frac{1}{1-n}}+\mathcal {O}\big (\varepsilon ^{\frac{n}{n-1}}\big ), \end{aligned}$$
(55c)

where \(x_0\) and \(y_0\) are defined as in Eq. (2).

Table 1 Asymptotic expansions for Eq. (4) (Region III) and (5) (Regions I and II)
Full size table

Proof

As in the proof of Proposition 4, we consider the expressions for \((x,y)(t,\varepsilon )\) in Eq. (53); however, the particular solution now cannot be neglected, as \(\mathcal {O}(\varepsilon )={\scriptstyle \mathcal {O}}(\varepsilon ^{\frac{1}{n-1}})\) due to \(n>2\). To account for the contribution therefrom to (53a), for instance, we expand the integrand and then evaluate the resulting leading-order integral to find

$$\begin{aligned} \begin{aligned}&\int _{\frac{1}{n-1}(1-\varepsilon u_0^{1-n})}^t \sin (t-s)\big [(n-1)s+\varepsilon u_0^{1-n}\big ]^{\frac{1}{1-n}}\,ds \\&\quad =\frac{n-1}{n-2}t[(n-1)t]^{\frac{1}{1-n}}{_1}F_2\big (\tfrac{n-2}{2n-2};\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{t^2}{4}\big )\sin (t) \\&\qquad -\frac{n-1}{2n-3}t^2[(n-1)t]^{\tfrac{1}{1-n}}{_1}F_2\big (\tfrac{2n-3}{2n-2};\tfrac{3}{2},\tfrac{4n-5}{2n-2};-\tfrac{t^2}{4}\big )\cos (t) \\&\qquad -\frac{1}{n-2}{_1}F_2\big (\tfrac{n-2}{2n-2};\tfrac{1}{2},\tfrac{3n-4}{2n-2};-\tfrac{1}{4(n-1)^2}\big )\sin (t) \\&\qquad +\frac{1}{(n-1)(2n-3)}{_1}F_2\big (\tfrac{2n-3}{n-2};\tfrac{3}{2},\tfrac{4n-5}{2n-2};\\&\qquad -\tfrac{1}{4(n-1)^2}\big )\cos (t)+\mathcal {O}(\varepsilon ). \end{aligned} \end{aligned}$$
(56)

Substituting (56), as well as the expansions for \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) from (48), into (53a) and expanding the result in \(\varepsilon \), we obtain the expansion for \(x(t,\varepsilon )\) in Eq. (55a), as claimed. The expansion for \(y(t,\varepsilon )\) in (55b) is derived in an analogous fashion. Finally, Eq. (55c) is obtained as in the proof of Proposition 4; recall (52c). \(\square \)

Fig. 7
figure 7

Absolute error between the asymptotics in Eqs. (52) (\(1<n<2\)), (5) (\(n=2\)), and (6) (\(n>2\)) and a numerical solution of Eq. (4) for \(\varepsilon \in [0.0023,0.012]\) and \(t_*=50\)

Full size image
Fig. 8
figure 8

Representative time series of \(y(t,\varepsilon )\), as obtained from the asymptotics in Eqs. (52), (5), and (6) (magenta) and a numerical solution of Eq. (4) (red), for varying values of n and \(\varepsilon \)

Full size image

We emphasize that the expansions derived in Propositions 1 through 3 do not depend on the arbitrary definition of the intermediate sections \(\Sigma _1^{\mathrm{in}}(\equiv \Sigma ^{\mathrm{in}})\) and \(\Sigma _1^{\mathrm{out}}(\equiv \Sigma _2^{\mathrm{in}})\), as is to be expected; in particular, there is no \(r_0\)-dependence in these expansions.

We summarize our asymptotic expansions for the solutions to Eqs. (4) and (5) in regions I, II, and III in the following Table 1; here, we recall that \(\tau ^{\mathrm{in}}=\frac{1}{n-1}\big (r_0^{1-n}-u_0^{1-n}\big )\) and \(t^{\mathrm{out}}=\varepsilon \tau ^{\mathrm{out}}=\frac{1}{n-1}(1-\varepsilon u_0^{1-n})\). Moreover, we note that, in order to be able to write \((x_1,y_1,r_1)(\varepsilon _1)\) in terms of the original variables \((\tau ,\varepsilon )\) from Eqs. (42) and (47), we need to express \(\varepsilon _1\) as a function of those variables:

Lemma 5

Let \(\varepsilon \in (0,\varepsilon _0]\), with \(\varepsilon _0>0\) sufficiently small, and let \(\varepsilon _1\) be defined as in Eq. (21); then,

$$\begin{aligned} \varepsilon _1(\tau ,\varepsilon )=\varepsilon \big [(n-1)\tau +u_0^{1-n}\big ]. \end{aligned}$$
(57)

Proof

We recall that \(\varepsilon _1=\frac{\varepsilon }{r_1^{n-1}}=\frac{\varepsilon }{u^{n-1}}\), by (21); substituting for \(u(\tau )\) from Eq. (10c), we obtain (57), as claimed. \(\square \)

To reiterate, the “inner” expansion obtained in region I is a regular perturbation expansion for the solution to the fast system, Eq. (5); it is valid on an \(\mathcal {O}(1)\)-interval in the fast time \(\tau \) or, equivalently, for \(t=\mathcal {O}(\varepsilon )\), capturing the rapid initial decay toward \(\{u=0\}\). The long-time behavior of solutions is captured by the “outer” expansion in region III, which is uniformly valid in the slow time t, for \(t=\mathcal {O}(1)\) as \(\varepsilon \rightarrow 0\). These expansions are matched in the “intermediate” region II; in particular, the expressions for \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) that are obtained in the transition through that region correspond to the matching conditions given in [14].

5 Conclusions

In this article, we have presented a geometric analysis of a singularly perturbed two-body problem with quick loss of mass that was first proposed by Verhulst in [14]. Our aim was two-fold: first, we wanted to show that geometric singular perturbation theory [5, 6], in combination with geometric desingularization (“blow-up”) [4, 7], is well-suited to the analysis of such problems. Second, we wanted to explain geometrically the matching conditions imposed in [14], in the derivation of Verhulst’s matched asymptotic expansions. Our conclusions can be summarized as follows.

  1. (1)

    In contrast to the asymptotic matching performed in [14], whereby “inner” and “outer” expansions are assumed without much justification, the unexpected-seeming scaling in powers of \(\varepsilon ^{\frac{1}{n-1}}\) in the resulting asymptotics appears naturally here after blow-up. Furthermore, the occurrence of logarithmic switchback terms in \(\varepsilon \) is explained through resonances between the eigenvalues of the linearization of the governing equations in the phase-directional chart \(K_1\) in the blow-up space [11]. The matching procedure applied in [14] is thus justified rigorously via our description of the transition through region II in \(K_1\), which establishes the connection between regions I and III. That region corresponds to an “intermediate” scaling in (5) which is equivalent to the domain of overlap that is conventionally introduced in matching. Our analysis complements that in [16], in the sense that no explicit small-\(\varepsilon \) approximation for \(x_1^{\mathrm{out}}\) and \(y_1^{\mathrm{out}}\) was derived there, which precluded a detailed comparison with [14]. Correspondingly, our asymptotic expansions for \(1<n<2\) and \(n=2\) agree with those of Verhulst after blow-down, i.e., after transformation to the original state variables x and \(\dot{x}\); for \(n>2\), we obtain more explicit expansions than are given in [14].

  2. (2)

    Numerical simulation confirms the expected error of our “outer” asymptotics in \(\varepsilon \), as stated in Eqs. (52), (5), and (6), respectively; cf. Fig. 7, where \(\varepsilon \) up to \(\mathcal {O}(10^{-2})\) is considered. Here, \(\Delta x(t_*,\varepsilon )\) and \(\Delta y(t_*,\varepsilon )\) denote the absolute error in x and y, respectively, between our asymptotics for \(x(t,\varepsilon )\) and \(y(t,\varepsilon )\), respectively, and a numerical solution of (4) that was obtained in Mathematica with 8-digit relative and absolute precision, where we have chosen \(t_*=50\). Throughout, we observe agreement with the expected order of the error in \(\varepsilon \). We emphasize that, when \(1<n<2\), the error behaves like \(\mathcal {O}(\varepsilon ^2)\) as \(\varepsilon \rightarrow 0\) for \(1<n<\frac{3}{2}\) and like \(\mathcal {O}(\varepsilon ^{\frac{1}{n-1}})\) for \(\frac{3}{2}<n<2\), which is in agreement with Eq. (52); see again Fig. 7. (The magnitude of the absolute error is due to the numerical value of the corresponding coefficient, which can well be of the order 10 for some values of n.) For illustrative purposes, we also visualize representative time series of \(y(t,\varepsilon )\) for various values of n and \(\varepsilon \) in Fig. 8; here, our asymptotics is displayed in magenta, whereas the numerical solution, which was obtained in Matlab using the standard solver ode45 with default parameters, is plotted in red. We note good agreement on the scale of the figure for moderate values of \(\varepsilon \), as well as an apparent increase in the accuracy of our asymptotics with increasing n.

  3. (3)

    On a related note, we emphasize that we do not address the question of the optimal truncation of the asymptotic expansions in the various regions, as summarized in Table 1. Since the derivation of these expansions is based on singular perturbation techniques, with \(\varepsilon \) the (small) perturbation parameter, they are only guaranteed to approximate the solution to (4) well for sufficiently small \(\varepsilon \); being asymptotic series, they are expected to diverge. Unlike in the theory of convergent power series, one hence does not automatically obtain a better approximation by including more terms in the truncation. The optimal truncation point, which will typically depend on \(\varepsilon \), can be determined by investigating the so-called Gevrey properties of these series expansions; see, e.g. [10] for details and references.

  4. (4)

    While the singularly perturbed system in Eq. (5) is atypical, in that it admits an explicit solution in terms of (generalized) hypergeometric functions in the phase-directional chart, the geometric approach showcased here can equally be applied to systems where no such solutions are available; as is common practice in the application of blow-up, the corresponding transition maps through those charts can be approximated using well-adapted normal forms and invariant manifold techniques.

  5. (5)

    Finally, it may appear that our simplifying assumption of \(f\equiv 1\) in Eq. (1) is restrictive. However, it can be shown that our analysis will remain valid for more general f provided (3) holds, in agreement also with [14]. If f is time-independent, a regular expansion as in Eq. (16) can still be found in region I; due to the fact that no explicit expression for u will be available in general, that expansion will depend on the Taylor series of f about \((x,y,\varepsilon )=(x_0,y_0,0)\). In region III, the f-dependence of \(u_2\)—and, correspondingly, of the integral terms in Eq. (30)—will merely introduce higher-order corrections (in \(r_2\)) in the resulting asymptotics. Similarly, in region II, the dynamics of \(r_1\) will be f-dependent, affecting our description of the transition through that region at higher order in \(\varepsilon _1\); in particular, the corresponding Eq. (40) may no longer be solvable exactly in terms of special functions. If, additionally, f is permitted to depend on time in (3), further complications arise due to the vector field in (4) being non-autonomous then; however, those can be remedied by including time as an artificial dependent variable both in Eq. (4) and in the blow-up transformation in (20), and by expanding the function f about \((t,x,y,\varepsilon )=(0,x_0,y_0,0)\). In sum, the qualitative dynamics of (1) will remain unaffected by the specific choice of f given Eq. (3), which is corroborated by numerical simulation; recall Figs. 1 and 2.