1 Introduction

The dynamic behavior of coupled vehicle–bridge systems is a topic of increasing interest. A main reason for that is the vast expansion of high-speed railway (HSR) networks worldwide [1]. As of 2019, China possesses the world’s most extensive HSR network (35,000 km) [2] and plans to further expand it to over 80,000 km [3] by 2030. A characteristic of contemporary HSR lines is the large proportion of bridges they are made up of [4]. In some cases, bridges constitute over 90% of the total length of an HSR line [4]. For example, the Guangzhou–Zhuhai intercity railway line in China, with total length 142.3 km, consists of 94.2% bridges [4]. The increasing ratio of bridges in HSR lines, in conjunction with the high speeds at which HSR trains operate (about 300-350 km/h) [5], has led to a proliferating research on the vehicle–bridge interaction (VBI) phenomenon [6,7,8,9,10,11,12,13], as well as to code provisions that aim at the safety and comfort of HSR transportation [14,15,16].

To elucidate the coupling mechanisms between vehicles and bridges, seminal studies [8, 17, 18] investigated analytically simple VBI configurations. Pesterev et al. [18] examined a moving oscillator traversing a simple beam and identified the oscillator’s stiffness as a major coupling parameter. That study illustrated that for very low and very high spring stiffness, the moving oscillator problem reduces, respectively, to the moving load problem and the moving mass problem. Yang et al. [8] showed that for small vehicle-to-bridge mass ratio, the vehicle acts as a moving load to the supporting bridge. Subsequent studies [19, 20] confirmed these findings [8, 18] numerically through parametric analyses for various vehicle and bridge systems. A recent study by the authors [21] stressed the importance of the impedance ratio, defined as the ratio of the vehicle’s damping and bridge’s mechanical impedance, as a dominant coupling parameter.

For the purpose of bridge design, it is beneficial to decouple vehicle–bridge systems. The simplest approach is the well-known moving load approximation, which treats vehicles as moving loads on the supporting bridge [22, 23]. As an improvement, Eurocode proposes combining the moving load approximation with a damping ratio, in addition to the structural damping of the bridge, to account for the favorable damping effect of VBI [20, 24,25,26]. This additional damping method (ADM) [14] applies to simply supported bridges and recommends an additional damping ratio [14] that is merely a function of the bridge’s length. Later studies [24,25,26] showed that the ADM does not accurately estimate the additional damping effect of VBI on a bridge, as this actually depends on the dynamic characteristics of both vehicle and bridge. These studies [25, 26] also offer analytical formulas to estimate the additional damping ratio for different types of bridges. Furthermore, Eurocode suggests an amplification factor \({\varphi }''\) to estimate the increase in the vibration of a bridge due to the irregularities in the rails [14]. However, in many cases, \({\varphi }''\) underestimates the effect of rail irregularities on the bridge response, and especially acceleration [21, 27].

Recently, the authors [21] proposed an approach to characterize and decouple the VBI problem for simply supported bridges—the Modified Bridge System (MBS) method. This method captures both additional damping and effect of irregularities, as well as, the additional stiffness effect of VBI on the response of the supporting bridge. The MBS method is limited by (a) the assumption of solely a single degree of freedom (SDOF) for the vehicle and an SDOF for the bridge, and (b) by the exclusion of the effect of the mass of the wheels. As a result, the MBS is insufficient for estimating the response of more complicated bridge models (e.g., continuous bridges), as well as to capture the acceleration of even simple bridges (e.g., simply supported), due to higher-order effects. The importance of the bridge deck acceleration is evident in contemporary design standards, such as Eurocode [14], the Chinese Code for Design of High-Speed Railway [15] and the International Union of Railways (UIC) code [16], which set deck acceleration limits to ensure riding comfort and ballast stability (as pertinent serviceability limit states (SLS)).

The present study extends the previous work of the authors [21, 26], to the case of multi-degree of freedom (MDOF) vehicle–MDOF bridge systems, representative of practical (conventional and high speed) train–bridge systems. The study decouples the VBI dynamics, in the vertical plane, through an asymptotic expansion analysis of the response of the coupled system [28], and proposes decoupling formulations applicable to any bridge type. Different to the formerly presented MBS method [21], the consideration of MDOF vehicle and MDOF bridge models also enables the accurate prediction of the bridge deck acceleration.

Fig. 1
figure 1

A 10-DOF train vehicle traversing a generic bridge (notation is given in “Appendix B”)

Full size image

2 Vehicle–bridge interaction: problem formulation

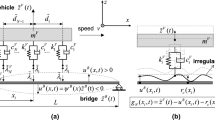
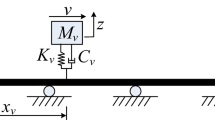
This section formulates the equations of motion (EOMs) of an MDOF vehicle traversing a generic MDOF bridge (Fig. 1). The goal is to examine the dynamics of vehicle–bridge systems in the vertical plane and break down the coupling mechanisms of VBI of MDOF vehicle–MDOF bridge systems.

2.1 Vehicle subsystem

The EOM of the vehicle is considered about its statically deformed configuration under its self-weight. To facilitate the decoupling of the vehicle–bridge system, the EOM of the MDOF vehicle of Fig. 1 is partitioned into the degrees of freedom (DOFs) not in contact with the bridge—upper part  \({\tilde{\mathbf {u}}}^{u}\left( t \right) \)—and the DOFs in contact with the bridge—wheels part  \({\tilde{\mathbf {u}}}^{w}\left( t \right) \):

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{{{\mathbf {m}}}^u}}&{}{{\mathbf {0}}} \\ {{\mathbf {0}}}&{}{{{{\mathbf {m}}}^{\textit{w}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{{\ddot{\tilde{\mathbf {u}}}}}}^u}} \\ {{{{{\ddot{\tilde{\mathbf {u}}}}}}^{\textit{w}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\mathbf {c}}}^u}}&{}{{{{\mathbf {c}}}^{u,\textit{w}}}} \\ {{ {{{{\mathbf {c}}}^{w,\textit{u}}}}}}&{}{{{{\mathbf {c}}}^{\textit{w}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{{\dot{\tilde{\mathbf {u}}}}}}^u}} \\ {{{{{\dot{\tilde{\mathbf {u}}}}}}^{\textit{w}}}} \end{array}} \right] \nonumber \\&\quad + \left[ {\begin{array}{*{20}{c}} {{{{\mathbf {k}}}^u}}&{}{{{{\mathbf {k}}}^{u,{\textit{w}}}}} \\ {{ {{{{\mathbf {k}}}^{w,\textit{u}}}} }}&{}{{{{\mathbf {k}}}^{\textit{w}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{{\tilde{\mathbf {u}}}}}^u}} \\ {{{{{\tilde{\mathbf {u}}}}}^{\textit{w}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathbf {0}}} \\ {{{{\mathbf {W}}}^{\textit{w}}}} \end{array}} \right] {{\tilde{\varvec{\lambda }} }} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf {f}}}^u}} \\ {{{{\mathbf {f}}}^{\textit{w}}}} \end{array}} \right] \end{aligned}$$
(1)

\({{\mathbf {m}}}\), \({{\mathbf {c}}}\) and \({{\mathbf {k}}}\) denote the mass, damping and stiffness matrices of the upper part (superscript \(()^u\)) and of the wheels part (superscript \(()^{\textit{w}}\)) of the vehicle, and the coupling submatrices between the two parts (superscripts \(()^{u,w}\) and \(()^{w, u}\)). \(\varvec{\tilde{\lambda } }\left( t \right) \) is the vector of the contact forces between the vehicle and bridge subsystems. \({{\mathbf {W}}}^{w}\) is the contact direction matrix (of the wheels part) associating the contact forces with the DOFs of the vehicle. Note that the upper part of the vehicle is not in contact with the bridge; hence, the corresponding contact direction matrix is zero. \({\mathbf {{{f}}}}^{u}\) and  \({\mathbf {{{f}}}}^{w}\) are the external force vectors of the two parts of the vehicle. The focus herein is on VBI; thus, no external excitation is considered, and vectors \({\mathbf {{f}}}^{u}\) and  \({\mathbf {{f}}}^{w}\) are henceforth zero vectors. The tilde is used to distinguish dimensional from the corresponding dimensionless quantities, when needed (later on).

2.2 Bridge subsystem

Similar to the vehicle subsystem, the EOM of the bridge is:

$$\begin{aligned} {{{\mathbf {m}}}^{B}}{{{\ddot{\tilde{\mathbf {u}}}}}^{B}}+{{{\mathbf {c}}}^{B}}{{{\dot{\tilde{\mathbf {u}}}}}^{B}} +{{{\mathbf {k}}}^{B}}{{{{\tilde{\mathbf {u}}}}}^{B}}+{{{\mathbf {W}}}^{B}}\varvec{\tilde{\lambda }}={{{\mathbf {{f}}}}^{B}} \end{aligned}$$
(2)

where \({{{\mathbf {m}}}^{B}}\), \({{{\mathbf {c}}}^{B}}\) and  \({{{\mathbf {k}}}^{B}}\) are, respectively, the mass, damping and stiffness matrices of the bridge, and  \({{\tilde{\mathbf {u}}}^{B}}\left( t \right) \) is the response vector of the bridge’s DOFs. \({{{\mathbf {W}}}^{B}}\left( x \right) \) is the contact direction matrix of the bridge connecting the contact forces with the DOFs of the bridge (“Appendix A”). \({{{\mathbf {W}}}^{B}}\left( x \right) \) is time-dependent [11], as the location of the vehicle \(x=vt\) changes with time t. \({{\mathbf {{f}}}^B}\) is the external force vector acting on the bridge, including the forces due to the self-weight of the vehicle.

Throughout the study, an overdot indicates differentiation with respect to the dimensional time t, while prime denotes differentiation with respect to the dimensional location of the vehicle x.

2.3 Coupled VBI system

The EOM of the coupled vehicle–bridge system (Eqs. (1) to (2)) is:

$$\begin{aligned} \mathbf {m}\ddot{\tilde{\mathbf {u}}}+\mathbf {c}\dot{\tilde{\mathbf {u}}}+\mathbf {k}\tilde{\mathbf {u}}-{\mathbf {W}}\varvec{\tilde{\lambda }}=\mathbf {{f}} \end{aligned}$$
(3)

where \({{\tilde{\mathbf {u}}}}\left( t \right) \) is the displacement vector of the whole (coupled) system:

$$\begin{aligned} {{{\tilde{\mathbf {u}}}}^{T}}={{\left[ \begin{matrix} \left[ \begin{matrix} ({{{\tilde{\mathbf {u}}}}^{u}})^T&{} ({{{\tilde{\mathbf {u}}}}^{\textit{w}}})^T \\ \end{matrix} \right] &{} ({{{\tilde{\mathbf {u}}}}^{B}})^T \\ \end{matrix} \right] }}. \end{aligned}$$
(4)

Superscript \(()^{\text {T}}\) denotes the transpose of a vector or matrix. \({{{\mathbf {m}}}}\), \({{{\mathbf {c}}}}\) and  \({{{\mathbf {k}}}}\) are the corresponding mass, damping and stiffness matrices of the entire system:

$$\begin{aligned} {{\mathbf {m}}}= & {} \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf {m}}}^u}}&{}{{\mathbf {0}}} \\ {{\mathbf {0}}}&{}{{{{\mathbf {m}}}^{\textit{w}}}} \end{array}} \right] }&{}{{\mathbf {0}}} \\ {{\mathbf {0}}}&{}{{{{\mathbf {m}}}^B}} \end{array}} \right] , \nonumber \\ {{\mathbf {c}}}= & {} \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf {c}}}^u}}&{}{{\mathbf {c}}}^{u,w} \\ {{\mathbf {c}}}^{w,u}&{}{{\mathbf {c}}}^{w} \end{array}} \right] }&{}{{\mathbf {0}}} \\ {{\mathbf {0}}}&{}{{{{\mathbf {c}}}^B}} \end{array}} \right] ,\\ {{\mathbf {k}}}= & {} \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf {k}}}^u}}&{}{{\mathbf {k}}}^{u,w} \\ {{\mathbf {k}}}^{w,u}&{}{{{{\mathbf {k}}}^{{w}}}} \end{array}} \right] }&{}{{\mathbf {0}}} \\ {{\mathbf {0}}}&{}{{{{\mathbf {k}}}^B}}\nonumber \end{array}} \right] . \end{aligned}$$
(5)

For the generic 2D vehicle of Fig. 1,  \({{\tilde{\mathbf{u}}}}^{{w}}\) contains only translational DOFs along the vertical direction (“Appendix B”); thus,  \({{{\mathbf {W}}}^{{w}}} = {{\mathbf{E}}}\), where \({\mathbf{{E}}}\) is the identity matrix. The contact direction matrix \({\mathbf {W}}\left( x \right) \) and the external force vector \({{\mathbf {{f}}}}\) of the entire system take, respectively, the form:

$$\begin{aligned} {\mathbf {W}}=\left[ \begin{matrix} \left[ \begin{matrix} {\mathbf {0}} \\ {{{\mathbf {E}}}} \\ \end{matrix} \right] \\ -{{{\mathbf {W}}}^{B}} \\ \end{matrix} \right] \ \ \text {and}\ \ \mathbf {{f}}=\left[ \begin{matrix} \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {0}} \\ \end{matrix} \right] \\ {{{\mathbf {{f}}}}^{B}} \\ \end{matrix} \right] . \end{aligned}$$
(6)

To estimate the contact force \(\varvec{\tilde{\lambda } }\), the study assumes “rigid contact” between the wheels and the rails [11]. This assumption implies continuous contact, and subsequently zero relative displacement/acceleration  \({\mathbf {g}}_{N}\left( x,t \right) ={{{\ddot{\mathbf {g}}}}_{N}}\left( x,t \right) ={\mathbf {0}}\), between the wheels and the rails at all times [11]. The relative displacement between the two subsystems is:

$$\begin{aligned} {{{\mathbf {g}}}_{N}}={{{\mathbf {W}}}^{\text {T}}}\tilde{\mathbf {u}}-{{{\mathbf {r}}}_{c}}={{{\tilde{\mathbf {u}}}}^{w}}-{{\left( {{{\mathbf {W}}}^{B}} \right) }^{\text {T}}}{{{\tilde{\mathbf {u}}}}^{B}}-{{{\mathbf {r}}}_{c}} \end{aligned}$$
(7)

where \({{{\mathbf {r}}}_c}\left( {x} \right) \) is the irregularities vector, consisting of the irregularities  \({r_{c}}\left( x_i \right) \) at each contact point (Fig. 2).

The irregularities are simulated as stationary stochastic processes with the spectral representation method [8]. The relative velocity \({{\dot{\mathbf {g}}}_{N}}\left( x,t \right) \) results by differentiating the relative displacement vector (Eq. (7)) with respect to time t:

$$\begin{aligned} \begin{aligned} {{\dot{\mathbf {g}}}_N}&= {{{\mathbf {W}}}^{\text {T}}}{{\dot{\tilde{\mathbf {u}}}}} + v{{{\mathbf {W'}}}^{\text {T}}}{{\tilde{\mathbf {u}}}} - v{{{\mathbf {r}}}}'_c \\&= {{{{\dot{\tilde{\mathbf {u}}}}}}^{{w}}} - v{\left( {{{{\mathbf {W}}}^B}} \right) ^\prime }^{\text {T}}{{{{\tilde{\mathbf {u}}}}}^B} - {\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}{{{{\dot{\tilde{\mathbf {u}}}}}}^B} - v{{{\mathbf {r}}}}'_c. \end{aligned} \end{aligned}$$
(8)

Accordingly, the relative acceleration is:

$$\begin{aligned} {{{\ddot{\mathbf {g}}}}_{N}}={{{\mathbf {W}}}^{\text {T}}}\ddot{\tilde{\mathbf {u}}}+2v{{{\mathbf {{W}'}}}^{\text {T}}}\dot{\tilde{\mathbf {u}}}+{{v}^{2}}{{{\mathbf {{W}''}}}^{\text {T}}}\tilde{\mathbf {u}}-{{v}^{2}}{{{\mathbf {{r}}}}_{c}''}. \end{aligned}$$
(9)

Applying the kinematic constraint on the acceleration level  \({{{\ddot{\mathbf {g}}}}_{N}}={\mathbf {0}}\) and substituting  \({\ddot{\tilde{\mathbf {u}}}}\) (from Eq. (9)) into the system’s EOM (Eq. (3)) give the contact force:

$$\begin{aligned} {{\tilde{\varvec{\lambda }} }} = - {{{\mathbf {G}}}^{ - 1}}\left[ \begin{array}{l} {{{\mathbf {W}}}^{\text {T}}}{{{\mathbf {m}}}^{ - 1}}\left( {{{\mathbf {f}}} - {\mathbf {c}\dot{\tilde{\mathbf {u}}}} - {\mathbf {k}{\tilde{\mathbf {u}}}}} \right) \\ + 2v{{{\mathbf {W'}}}^{\text {T}}}{{\dot{\tilde{\mathbf {u}}}}} + {v^2}{{{\mathbf {W''}}}^{\text {T}}}{{\tilde{\mathbf {u}}}} - {v^2}{{{\mathbf {r}}}}''_c \end{array}\right] . \end{aligned}$$
(10)

In Eq. (10), \({{{\mathbf {{G}}}}^{-1}}\) is the mass participating in the contact interaction between the wheels and the bridge. Its inverse \({{\mathbf {{G}}}}\) is:

$$\begin{aligned} \mathbf {{G}}={{{\mathbf {W}}}^{\text {T}}}{{{\mathbf {m}}}^{-1}}{\mathbf {W}}={{\left( {{{\mathbf {m}}}^{w}} \right) }^{-1}}+{{\left( {{{\mathbf {W}}}^{B}} \right) }^{\text {T}}}{{\left( {{{\mathbf {m}}}^{B}} \right) }^{-1}}{{{\mathbf {W}}}^{B}}.\nonumber \\ \end{aligned}$$
(11)

Substituting the system matrices \({\tilde{\mathbf {u}}}\),  \({{\mathbf {m}}}\), \({{\mathbf {c}}}\), \({{\mathbf {k}}}\),  \({{\mathbf {W}}}\) and \({\mathbf {{f}}}\) (Eqs. (4) to (6)), as well as the wheels response \({{\tilde{\mathbf {u}}}^{{w}}}\) (from the kinematic constraints \({{{\mathbf {g}}}_{N}}={\mathbf {0}}\) (Eq. (7)) and  \({{{\dot{\mathbf {g}}}}_{N}}={\mathbf {0}}\) (Eq. (8))) into Eq. (10), the contact force  \(\varvec{\tilde{\lambda } }\) becomes:

(12)

Subsequently, substituting \(\varvec{\tilde{\lambda }}\) (Eq. (12)) into Eq. (2), the bridge’s EOM becomes:

(13)
Fig. 2
figure 2

a “Very good” and b “good” quality rail irregularities sample according to the German spectra, with reference to HSR [29]

Full size image

Note that after the introduction of the kinematic constraints (Eqs. (7) and (8)) into the contact force (Eq. (10)), the DOFs of the wheels \({{\tilde{\mathbf {u}}}^{{w}}}\) vanish from Eqs. (12), (13) and henceforth. Thus, the EOM of the bridge (Eq. (13)) includes solely the response of the vehicle’s upper part.

Similarly, the EOM of the upper part of the vehicle becomes:

$$\begin{aligned}&{{{\mathbf {m}}}^u}{{{{\ddot{\tilde{\mathbf {u}}}}}}^u} + {{{\mathbf {c}}}^u}{{{{\dot{\tilde{\mathbf {u}}}}}}^u} + {{{\mathbf {k}}}^u}{{{{\tilde{\mathbf {u}}}}}^u}\nonumber \\&\quad = - {{{\mathbf {c}}}^{u,\textit{w}}}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}{{{{\dot{\tilde{\mathbf {u}}}}}}^B} + v{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}{{{{\tilde{\mathbf {u}}}}}^B} + v{{{\mathbf {r}}}}'_c} \right) \nonumber \\&\qquad - {{{\mathbf {k}}}^{u,\textit{w}}}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}{{{{\tilde{\mathbf {u}}}}}^B} + {{{\mathbf {r}}}_c}} \right) . \end{aligned}$$
(14)

Equations (13) and (14) describe the coupled system in a minimal manner (i.e., with the minimum number of DOFs) [30].

3 Dimensionless description of the problem

To identify the constituent mechanisms of VBI on the mechanical system of the bridge, this section formulates the EOMs of the vehicle and bridge subsystems (Eqs. (13) and (14)) in dimensionless terms. As the interest is mainly on the bridge subsystem, the dimensionless equations are expressed with reference to the length L, eigenfrequency \(\omega ^B\) and generalized mass \(m^B\) of the first mode of the bridge, similar to the previous study of the authors on an SDOF vehicle–SDOF bridge system [21]. Thus, the dimensionless contact force vector \(\varvec{\lambda }\) (Eq. (12)) is:

$$\begin{aligned} {\varvec{\lambda }}= & {} \frac{1}{{{m^B}{\omega ^B}}} {{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {m}}}^{\textit{w}}}} \right) ^{ - 1}}\left( {{{\mathbf {c}}}^{\textit{w},u}}{{\dot{\mathbf {u}}}^u} + {{{\mathbf {c}}}^{\textit{w}}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}{{\dot{\mathbf {u}}}^B} + S_v{{{\mathbf {c}}}^{\textit{w}}}{\left( {{{{\mathbf {W}}}^B}} \right) ^\prime }^{\text {T}}{{{\mathbf {u}}}^B} \right. \nonumber \\&\quad \left. + {S_v}{{{\mathbf {c}}}^{\textit{w}}}{{{\mathbf {R}}}}'_c\right) + \frac{1}{{{m^B}{{\left( {{\omega ^B}} \right) }^2}}}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {m}}}^{\textit{w}}}} \right) ^{ - 1}} \left( {{{\mathbf {k}}}^{\textit{w},u}}{{{\mathbf {u}}}^u} + {{{\mathbf {k}}}^{\textit{w}}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}{{{\mathbf {u}}}^B} + {{{\mathbf {k}}}^{\textit{w}}}{{{\mathbf {R}}}_c} \right) \nonumber \\&\quad + \frac{1}{{{m^B}{\omega ^B}}}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}} \left( \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}L}}{{{\mathbf {f}}}^B} { - {{{\mathbf {c}}}^B}{{\dot{\mathbf {u}}}^B} - \frac{1}{{{\omega ^B}}}{{{\mathbf {k}}}^B}{{{\mathbf {u}}}^B}} \right) \nonumber \\&\quad + \frac{1}{{{m^B}}}{{{\mathbf {G}}}^{ - 1}} \left( {2{S_v}{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}{{\dot{\mathbf {u}}}^B} + S_v^2{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\prime \prime }}^{\text {T}}{{{\mathbf {u}}}^B} + S_v^2{{{\mathbf {R}}}}''_c} \right) \end{aligned}$$
(15)

consisting of the dimensionless contact forces \({\lambda _i}={{{\tilde{\lambda _i }}}}/{\left[ {{m}^{B}}{{\left( {{\omega }^{B}} \right) }^{2}}L \right] }\) at each point i. \({{{\mathbf {u}}}^{B}}={1}/{L}\;{{\tilde{\mathbf {u}}}^{B}}\) and  \({{{\mathbf {u}}}^{u}}={1}/{L}\;{{\tilde{\mathbf {u}}}^{u}}\) are the (dimensionless) displacement vectors of the bridge and of the vehicle’s upper part, respectively, both scaled with respect to  L. \({{S}_{v}}={v}/{\left( {{\omega }^{B}}L \right) }\) is the speed parameter [8] (Table 1), and  \(\tau ={{\omega }^{B}}t\) is the dimensionless time. Lastly,  \({{{\mathbf {R}}}_{c}}={{L}^{-1}}{{{\mathbf {r}}}_{c}}\),  \({{{\mathbf {{R}}}}'_{c}}={{{\mathbf {{r}}}}'_{c}}\) and  \({{{\mathbf {{R}}}}''_{c}}=L{{{\mathbf {r}}}''_{c}}\) are the dimensionless irregularities vectors (Table 1).

Assume \(k_p^V\) is the stiffness and \(c_p^V\) is the damping of the primary suspension system of the generic vehicle of Fig. 1. Then, the stiffness \({{{\mathbf {k}}}^{{w}}}\) and damping \({{{\mathbf {c}}}^{w}}\) submatrices of the vehicle’s wheels part can be written as \({{{\mathbf {k}}}^{{w}}} = diag\left\{ {k_p^V} \right\} \) and \({{{\mathbf {c}}}^{w}} = diag\left\{ {c_p^V} \right\} \), respectively (“Appendix B”). The wheels’ mass matrix is a diagonal matrix \({{{\mathbf {m}}}^{w}}=diag\left\{ {{m}^{w}} \right\} \), where \(m^{{w}}\) is the mass of each wheel. Similarly, the stiffness \({{{\mathbf {k}}}^{u,{w}}}\) and damping  \({{{\mathbf {c}}}^{u,{w}}}\) submatrices, connecting the vehicle’s upper part with the wheels part (“Appendix B”), are accordingly:

$$\begin{aligned} {{{\mathbf {k}}}^{u,{w}}} = k_p^V{{{\mathbf {W}}}^*}\;\;{\text {and}}\;\;{{{\mathbf {c}}}^{u,{w}}} = c_p^V{{{\mathbf {W}}}^*} \end{aligned}$$
(16)

where, for example (“Appendix B”), \( {{{\mathbf {W}}}^*}\) is:

$$\begin{aligned} {{{\mathbf {W}}}^{*}}=\left[ \begin{matrix} 0 &{} 0 &{} -1 &{} {{{l}_{w}}}/{L}\; &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} -{{{l}_{w}}}/{L}\;\ &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -1 &{} {{{l}_{w}}}/{L}\; \\ 0 &{} 0 &{} 0 &{} 0 &{} -1 &{} -{{{l}_{w}}}/{L}\;\ \\ \end{matrix} \right] \end{aligned}$$
(17)

with \({{l}_{w}}\) being half of the wheelbase (Fig. 1).

Matrix \({{{\mathbf {W}}}^*}\) is dimensionless and of order  \(O\left( {{{\mathbf {W}}}^*}\right) = {1}\). Therefore, it allows to capture the scale of the pertinent submatrices  \({{\mathbf {k}}}^{u,{w}}\) and \({{{\mathbf {c}}}^{u,{w}}}\) via the scalar parameters \(k_p^V\) and \(c_p^V\) of the primary suspension, respectively, facilitating the asymptotic expansion analysis of the next section (Sect. 4.1). Substituting the diagonal matrices \({{{\mathbf {k}}}^{{w}}}\), \({{{\mathbf {c}}}^{{w}}}\) and \({{{\mathbf {m}}}^{w}}\), and rewriting  \({{{\mathbf {k}}}^{u,{w}}}\) and \({{{\mathbf {c}}}^{u,{w}}}\) matrices with the aid of \( {{{\mathbf {W}}}^*}\) matrix, the dimensionless contact force (Eq. (15)) becomes:

(18)

\({{C}}={c_{p}^{V}}/{\left( {{m}^{B}}{{\omega }^{B}} \right) }\) is the impedance ratio of the primary suspension system of the vehicle [26], where \({{m}^{B}}{{\omega }^{B}}\) is the bridge’s mechanical impedance, denoting the resistance of the bridge to vibrations because of its mass [26]. \({{K}}={k_{p}^{V}}/{\left[ {{m}^{B}}{{\left( {{\omega }^{B}} \right) }^{2}} \right] }\;={k_{p}^{V}}/{{{k}^{B}}}\) represents the stiffness ratio of the primary suspension system of the vehicle with respect to the stiffness of the fundamental mode of the bridge. Clearly, the contact force (Eq. (18)) depends solely on the primary suspension system of the vehicle, connecting the bogies and the wheels (C and K), and includes the response of the bridge and of the vehicle’s upper part \({{{\mathbf {u}}}^u}\) (but not the response of the wheels part \({{{\mathbf {u}}}^{{w}}}\) (Eq. (12))).

Accordingly, the dimensionless EOM of the bridge (Eq. (13)) becomes:

$$\begin{aligned} \begin{aligned}&{{{\mathbf {M}}}^B}{{{{{\ddot{\mathbf {u}}}}}}^B} + \left( {{{\mathbf {C}}}^B} + C{{\mathbf {W}}}_{{\text {eff}}}^{\textit{w}} + 2{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{B,d} - \frac{1}{{{\omega ^B}}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {c}}}^B} \right) {{\dot{\mathbf {u}}}^B} \\&\quad \qquad + \left( {{{\mathbf {K}}}^B} + C{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{\textit{w},d} + K{{\mathbf {W}}}_{{\text {eff}}}^{\textit{w}}+ S_v^2{{\mathbf {W}}}_{{\text {eff}}}^{B,dd} - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {k}}}^B} \right) {{{\mathbf {u}}}^B} \\&\quad = {{{\mathbf {F}}}^B} - {{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}\left( {\frac{K}{{{m^{\textit{w}}}}}{{{\mathbf {R}}}_c} + \frac{{C{S_v}}}{{{m^{\textit{w}}}}}{{{\mathbf {R}}}}'_c + \frac{{S_v^2}}{{{m^B}}}{{{\mathbf {R}}}}''_c} \right) - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}L}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {f}}}^B} - {{\mathbf {W}}}_{{\text {eff}}}^{\textit{w}*}\left( {K{{{\mathbf {u}}}^u} + C{{\dot{\mathbf {u}}}^u}} \right) \end{aligned} \end{aligned}$$
(19)

where \({{{\mathbf {M}}}^{B}}=\left( {1}/{{{m}^{B}}} \right) {{{\mathbf {m}}}^{B}}\), \({{{\mathbf {C}}}^{B}}={1}/{\left( {{m}^{B}}{{\omega }^{B}} \right) }{{{\mathbf {c}}}^{B}}\) and  \({{{\mathbf {K}}}^{B}}={1}/{\left[ {{m}^{B}}{{\left( {{\omega }^{B}} \right) }^{2}} \right] }{{{\mathbf {k}}}^{B}}=\left( {1}/{{{k}^{B}}} \right) {{{\mathbf {k}}}^{B}}\) are the dimensionless (scaled) mass, damping and stiffness matrices of the bridge, and  \({{{\mathbf {F}}}^{B}}= {1}/{\left( {{k}^{B}}L \right) } {{{\mathbf {f}}}^{B}}\) is the dimensionless force vector acting on the bridge due to the vehicle’s self-weight (Table 1). For brevity, the following dimensionless matrices are introduced in Eq. (19):

$$\begin{aligned} \begin{aligned} {{\mathbf {W}}}_{{\text {eff}}}^B&= \frac{1}{{{m^B}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}, \\ {{\mathbf {W}}}_{{\text {eff}}}^{B,d}&= \frac{1}{{{m^B}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^\prime }^{\text {T}}, \\ {{\mathbf {W}}}_{{\text {eff}}}^{B,dd}&= \frac{1}{{{m^B}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\prime \prime }}^{\text {T}}, \\ {{\mathbf {W}}}_{{\text {eff}}}^{\textit{w}}&= \frac{1}{{{m^{\textit{w}}}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^{\text {T}}}, \\ {{\mathbf {W}}}_{{\text {eff}}}^{w,d}&= \frac{1}{{{m^{\textit{w}}}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{\left( {{{{\mathbf {W}}}^B}} \right) ^\prime }^{\text {T}}, \\ {{\mathbf {W}}}_{{\text {eff}}}^{w*}&= \frac{1}{{{m^{\textit{w}}}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{{{\mathbf {W}}}^*}. \end{aligned} \end{aligned}$$
(20)

Crucially, the response of the vehicle appears solely as loading on the right-hand side (RHS) of the EOM of the bridge (Eq. (19)), in the term  \({\mathbf {W}}_{\text {eff}}^{w*}\left( {{K}}{{{\mathbf {u}}}^{u}}+{{C}}{{{\dot{\mathbf {u}}}}^{u}} \right) \), and depends on the impedance C and stiffness K ratios.

Finally, the dimensionless EOM of the vehicle’s upper part is:

$$\begin{aligned}&\frac{1}{{{m^B}}}{{{\mathbf {m}}}^u}{{{{\ddot{\mathbf {u}}}}}^u} + \frac{1}{{{m^B}{\omega ^B}}}{{{\mathbf {c}}}^u}{{\dot{\mathbf {u}}}^u} + \frac{1}{{{m^B}{{\left( {{\omega ^B}} \right) }^2}}}{{{\mathbf {k}}}^u}{{{\mathbf {u}}}^u} \nonumber \\&\quad = - C{\left( {{{{\mathbf {W}}}^*}} \right) ^{\text {T}}}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}{{\dot{\mathbf {u}}}^B} {+} {S_v}{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}{{{\mathbf {u}}}^B} {+} {S_v}{{{\mathbf {R}}}}'_c} \right) \nonumber \\&\qquad - K{\left( {{{{\mathbf {W}}}^*}} \right) ^{\text {T}}}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}{{{\mathbf {u}}}^B} + {{{\mathbf {R}}}_c}} \right) . \end{aligned}$$
(21)

3.1 Constituent mechanisms of VBI on the mechanical system of the bridge

The EOM of the bridge (Eq. (19)) can be written as:

$$\begin{aligned}&{{{\mathbf {M}}}^B}{{{{\ddot{\mathbf {u}}}}}^B} {+} \left( {{{{\mathbf {C}}}^B} {+} {{{\mathbf {C}}}_{\text {I}}}\left( {x,{S_v}} \right) } \right) {{\dot{\mathbf {u}}}^B} {+} \left( {{{{\mathbf {K}}}^B} {+} {{{\mathbf {K}}}_{\text {I}}}\left( {x,{S_v}} \right) } \right) {{{\mathbf {u}}}^B}\nonumber \\&\quad = {{{\mathbf {F}}}^B} + {{{\mathbf {F}}}_{\text {I}}}\left( {{{{\mathbf {u}}}^u},{{\dot{\mathbf {u}}}^u}} \right) . \end{aligned}$$
(22)

Equation (22) shows that the effect of VBI on the bridge can be expressed via three terms: (a) an additional damping matrix term \({{{\mathbf {C}}}_{\text {I}}}\left( x,{{S}_{v}} \right) \), (b) an additional stiffness matrix term  \({{{\mathbf {K}}}_{\text {I}}}\left( x,{{S}_{v}} \right) \) and (c) an additional loading vector term \({{{\mathbf {F}}}_{\text {I}}}\left( {{{\mathbf {u}}}^{u}},{{{\dot{\mathbf {u}}}}^{u}} \right) \).

The additional damping term is:

$$\begin{aligned} {{{\mathbf {C}}}_{\text {I}}}\left( x,{{S}_{v}} \right) ={{C}}{\mathbf {W}}_{\text {eff}}^{w} + 2{{S}_{v}}{{{\mathbf {W}}_{\text {eff}}^{B,d} -\frac{1}{{{\omega }^{B}}}{\mathbf {W}}_{\text {eff}}^{B}{{\left( {{{\mathbf {m}}}^{B}} \right) }^{-1}}{{{\mathbf {c}}}^{B}} }} \nonumber \\ \end{aligned}$$
(23)

and corresponds to a time-varying additional damping matrix, mainly dependent on the impedance ratio C of the primary suspension system of the vehicle [26]. Details on the additional damping matrix and damping effect of VBI on bridges can be found in the authors’ previous study [26].

The additional stiffness term is also time-varying, as it depends on the location of the vehicle on the bridge:

$$\begin{aligned} \begin{aligned} {{{\mathbf {K}}}_{\text {I}}}\left( {x,{S_v}} \right)&= C{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{w,d} + K{{\mathbf {W}}}_{{\text {eff}}}^{w}+ S_v^2{{\mathbf {W}}}_{{\text {eff}}}^{B,dd} \\&\quad - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {k}}}^B} . \end{aligned} \end{aligned}$$
(24)

\({{{\mathbf {K}}}_{\text {I}}}\left( x,{{S}_{v}} \right) \) can acquire both positive and negative values and constitutes an alternative explanation of the change of the bridge’s natural frequencies during the passage of a vehicle [21, 31, 32]. It depends on both the impedance ratio C and the stiffness ratio  K of the vehicle’s primary suspension system.

Lastly, the additional loading vector is:

$$\begin{aligned} {{{\mathbf {F}}}_{\text {I}}}\left( {{{{\mathbf {u}}}^u},{{\dot{\mathbf {u}}}^u}} \right)&= - {{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}\left( {\frac{K}{{{m^{\textit{w}}}}}{{{\mathbf {R}}}_c} + \frac{{C{S_v}}}{{{m^{\textit{w}}}}}{{{\mathbf {R}}}}'_c + \frac{{S_v^2}}{{{m^B}}}{{{\mathbf {R}}}}''_c} \right) \nonumber \\&\quad - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}L}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {f}}}^B}\nonumber \\&\quad - {{\mathbf {W}}}_{{\text {eff}}}^{w*}\left( {K{{{\mathbf {u}}}^u} + C{{\dot{\mathbf {u}}}^u}} \right) . \end{aligned}$$
(25)

This term includes additional forces acting on the bridge due to irregularities, as well as due to the response of the traversing vehicle. Note that the vehicle response appears solely in the additional loading vector (Eq. (25)).

Table 1 Dimensionless groups of the coupled MDOF vehicle–MDOF bridge system
Full size table

4 A consistent decoupling methodology

The formulation of Eq. (22) is exact and informative regarding the constituent mechanisms of VBI on the mechanical system of the bridge. However, it still involves the fully coupled system, as the vehicle response (\({{{{\mathbf {u}}}}^u}\) and \({{\dot{\mathbf {u}}}^u}\)) appears into the bridge’s EOM (Eq. (22)) via terms associated with the dynamic properties of the vehicle’s primary suspension system (K and C) (Eq. (25)). Furthermore, Eq. (22) does not reveal the relative importance of the different VBI mechanisms.

The present section examines further the MDOF vehicle–MDOF bridge system (Eqs. (19) and (21)) and estimates the response of the bridge as an asymptotic expansion about a small dimensionless parameter \(\varepsilon \) (corresponding to a vehicle-to-bridge frequency ratio \({\varOmega }\)). This allows to determine the relative importance of the constituent VBI mechanisms and decouple the vehicle–bridge system by eliminating the vehicle response from the EOM of the bridge (Eq. (19)). This approach overcomes the limitations of the original MBS method [21], by extending its applicability to MDOF VBI systems.

4.1 Asymptotic expansion of coupled EOMs

Consider a frequency \(\omega ^p\), corresponding to the vehicle’s primary suspension system, defined as:

$$\begin{aligned} {\omega ^p} = \sqrt{\frac{{k_p^V}}{{{m^V}}}} \rightarrow k_p^V = {{{m^V}{{\left( {{\omega ^p}} \right) }^2}}} \end{aligned}$$
(26)

where \(m^V\) is the vehicle’s total mass and \(k_p^V\) is the stiffness of the primary suspension system. Accordingly, the damping of the primary suspension system is:

$$\begin{aligned} c_{p}^{V}=2{{m}^{V}}{{\omega }^{p}}{{\zeta }^{p}}\rightarrow {{\zeta }^{p}}=\frac{c_{p}^{V}}{2{{m}^{V}}{{\omega }^{p}}} \end{aligned}$$
(27)

where \(\zeta ^p\) is the corresponding damping ratio of the primary suspension system of the vehicle (Table 1). Note that  \(\omega ^p\) does not necessarily correspond to any of the natural frequencies of the vehicle.

Let \(M={{{m}^{V}}}/{{{m}^{B}}}\) denote the vehicle-to-bridge mass ratio and \({\varOmega } ={{{\omega }^{p}}}/{{{\omega }^{B}}}\) the eigenfrequency ratio (Table 1). With the aid of \(\zeta ^p\), M and \({\varOmega }\), and considering that \({{C}}=2M{\varOmega } {{\zeta }^{P}}\) and \({{K}}=M{{{\varOmega } }^{2}}\), the EOM of the bridge (Eq. (19)) becomes:

(28)

Accordingly, the EOM of the vehicle’s upper part (Eq. (21)) is:

$$\begin{aligned}&\frac{1}{{{m^B}}}{{{\mathbf {m}}}^{u}}{{{{\ddot{\mathbf {u}}}}}^u} + \frac{1}{{{m^B}{\omega ^B}}}{{{\mathbf {c}}}^u}{{\dot{\mathbf {u}}}^u} + \frac{1}{{{m^B}{{\left( {{\omega ^B}} \right) }^2}}}{{{\mathbf {k}}}^u}{{{\mathbf {u}}}^u}\nonumber \\&=-2M\Omega \zeta ^{p}\left( \mathbf{W} ^{*}\right) ^{\mathrm{T}} \left( \mathbf{W} ^B\right) ^{\mathrm{T}} \dot{\mathbf{u }}^{B}\nonumber \\&-2M\Omega \zeta ^{p}S_{v}\left( \mathbf{W} ^{*}\right) ^{\mathrm{T}} \left( \left( \mathbf{W} ^B\right) ^{'\mathrm{T}} \mathbf{u }^{B}+\mathbf{R} ^{'}_{c}\right) \nonumber \\&\qquad -M\Omega ^{2} \left( \mathbf{W} ^{*}\right) ^{\mathrm{T}}\left( \left( \mathbf{W} ^B\right) ^{'\mathrm{T}} \mathbf{u }^{B}+\mathbf{R} ^{'}_{c}\right) . \end{aligned}$$
(29)

For convenience, Table 1 illustrates all dimensionless groups introduced in this study.

In practice, the frequency ratio \({\varOmega }\) of the vehicle’s primary suspension system with respect to the fundamental frequency of the bridge obtains smalls values (e.g., \(O\left( {\varOmega } \right) = {10^{ - 1}}\)) [14, 33]. That converts the original VBI problem into a perturbation problem with small parameter  \(\varepsilon ={\varOmega }\).

For \(0 < \varepsilon \ll 1\), assume that the bridge response from Eq. (28) has an asymptotic expansion of the form:

$$\begin{aligned} \begin{aligned}&{{{\mathbf {u}}}^B} = {{\mathbf {u}}}_0^B + \varepsilon {{\mathbf {u}}}_1^B + {\varepsilon ^2}{{\mathbf {u}}}_2^B + O\left( {{\varepsilon ^3}} \right) \\&{{\dot{\mathbf {u}}}^B} = \dot{\mathbf {u}}_0^B + \varepsilon \dot{\mathbf {u}}_1^B + {\varepsilon ^2}\dot{\mathbf {u}}_2^B + O\left( {{\varepsilon ^3}} \right) \\&{{{{\ddot{\mathbf {u}}}}}^B} = {{\ddot{\mathbf {u}}}}_0^B + \varepsilon {{\ddot{\mathbf {u}}}}_1^B + {\varepsilon ^2}{{\ddot{\mathbf {u}}}}_2^B + O\left( {{\varepsilon ^3}} \right) \end{aligned} \end{aligned}$$
(30)

and accordingly for the response of the vehicle’s upper part (Eq. (29)), by changing superscript \({{\left( {} \right) }^{B}}\) to \({{\left( {} \right) }^{u}}\). Substituting Eq. (30) into the bridge’s EOM (Eq. (28)) and keeping only the zero-order terms in \(\varepsilon \), the zero-order EOM of the bridge is:

$$\begin{aligned}&{{{\mathbf {M}}}^B}{{\ddot{\mathbf {u}}}}_0^B + \left( {{{{\mathbf {C}}}^B} + 2{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{B,d}} - \frac{1}{{{\omega ^B}}}{{\mathbf {W}}}_{{\text {eff}}}^B{{\left( {{{{\mathbf {m}}}^B}} \right) }^{ - 1}}{{{\mathbf {c}}}^B} \right) \dot{\mathbf {u}}_0^B \nonumber \\&\qquad + \left( {{{{\mathbf {K}}}^B} + S_v^2{{\mathbf {W}}}_{{\text {eff}}}^{B,dd}} - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{{\left( {{{{\mathbf {m}}}^B}} \right) }^{ - 1}}{{{\mathbf {k}}}^B} \right) {{\mathbf {u}}}_0^B\nonumber \\&\quad = {{{\mathbf {F}}}^B} - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}{L^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {f}}}^B} - \frac{{S_v^2}}{{{m^B}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{{{\mathbf {R}}}}''_c \end{aligned}$$
(31)

which includes the external forces acting on the bridge due to the vehicle’s self-weight \({{{\mathbf {F}}}^{B}}\), as well as terms associated with the normalized contact mass \(\left( {1}/{{{m}^{B}}} \right) {{{\mathbf {G}}}^{-1}}\) (Eq. (20)), dependent on the normalized mass of the vehicle’s wheels  \({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\) (Eq. (11)), and the speed parameter \(S_v\). On the other hand, it neglects other dynamic characteristics of the vehicle (e.g., stiffness K and impedance  C ratios) and the vehicle response (Eq. (31)). In conclusion, the only vehicle parameters that affect the zero-order (in \(\varepsilon = {\varOmega }\)) response of the bridge (Eq. (31)) are the vehicle’s mass (through \({{{\mathbf {F}}}^{B}}\) and \({M}^{w}\) (Eq. (11))) and moving speed (through \(S_v\)).

Similarly, the zero-order response of the vehicle’s upper part (Eq. (29)) results from:

$$\begin{aligned} \frac{1}{{{m^B}}}{{{\mathbf {m}}}^u}{{\ddot{\mathbf {u}}}}_0^u + \frac{1}{{{m^B}{\omega ^B}}}{{{\mathbf {c}}}^u}\dot{\mathbf {u}}_0^u + \frac{1}{{{m^B}{{\left( {{\omega ^B}} \right) }^2}}}{{{\mathbf {k}}}^u}{{\mathbf {u}}}_0^u = {{\mathbf {0}}}. \end{aligned}$$
(32)

Equation (32) shows that, in the absence of external excitation, the zero-order response of the vehicle’s upper part is zero \({\mathbf {u}}_{0}^{u}={\mathbf {0}}\). Thus, in this case, the vehicle acts as a moving rigid body on the bridge.

For small mass of the wheels \({m}^{w}\) with respect to the generalized mass of the bridge \(m^B\) (\({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\;\ll 1\)), the dimensionless mass participating in the contact \(\left( {1}/{{{m}^{B}}} \right) {{{\mathbf {G}}}^{-1}}\) (Eq. (11)) converges to the dimensionless mass of the wheels (“Appendix B”), therefore:

$$\begin{aligned} \frac{1}{{{m^B}}}{{{\mathbf {G}}}^{ - 1}}&= \frac{1}{{{m^B}}}{\left( {{{\left( {{{{\mathbf {m}}}^{\textit{w}}}} \right) }^{ - 1}} + {{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}{{\left( {{{{\mathbf {m}}}^B}} \right) }^{ - 1}}{{{\mathbf {W}}}^B}} \right) ^{ - 1}}\nonumber \\&\approx {M^{\textit{w}}}{{\mathbf {E}}} \end{aligned}$$
(33)

where \({\mathbf {E}}\) is the identity matrix. Subsequently, the EOM of the bridge (Eq. (31)) reduces to:

$$\begin{aligned} {{{\mathbf {M}}}^{B}}\ddot{\mathbf {u}}_{0}^{B}+{{{\mathbf {C}}}^{B}}\dot{\mathbf {u}}_{0}^{B}+{{{\mathbf {K}}}^{B}}{\mathbf {u}}_{0}^{B}={{{\mathbf {F}}}^{B}} \end{aligned}$$
(34)

which solely depends on \({{{\mathbf {F}}}^{B}}\), as the terms associated with the dimensionless contact mass \(\left( {1}/{{{m}^{B}}} \right) {{{\mathbf {G}}}^{-1}}\) vanish from Eq. (31). This expression corresponds to the well-known moving load method.

Consequently, Eq. (34) shows that the moving load method is a zero-order (in \(\varepsilon = {\varOmega }\)) approximation of the bridge response (for small stiffness K and impedance C ratios of the primary suspension system of the vehicle), under the additional assumption of small normalized mass of the wheels with respect to the bridge’s generalized mass (\({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\ll 1\)). In other words, the moving load method is valid under multiple assumptions, which often are not (all of them) satisfied.

Next, the first order in \(\varepsilon \) bridge’s EOM (Eq. (28)) is:

$$\begin{aligned}&{{{\mathbf {M}}}^B}{{\ddot{\mathbf {u}}}}_1^B + \left( {{{{\mathbf {C}}}^B} + 2{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{B,d}} - \frac{1}{{{\omega ^B}}}{{\mathbf {W}}}_{{\text {eff}}}^B{{\left( {{{{\mathbf {m}}}^B}} \right) }^{ - 1}}{{{\mathbf {c}}}^B} \right) \dot{\mathbf {u}}_1^B \nonumber \\&\qquad + \left( {{{{\mathbf {K}}}^B} + S_v^2{{\mathbf {W}}}_{{\text {eff}}}^{B,dd}} - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{{\left( {{{{\mathbf {m}}}^B}} \right) }^{ - 1}}{{{\mathbf {k}}}^B} \right) {{\mathbf {u}}}_1^B\nonumber \\&\quad = - 2M{\zeta ^p}\left( {{\mathbf {W}}}_{{\text {eff}}}^{\textit{w}}\dot{\mathbf {u}}_0^B + {S_v}{{\mathbf {W}}}_{{\text {eff}}}^{w,d}{{\mathbf {u}}}_0^B\right. \nonumber \\&\qquad \left. + {{\mathbf {W}}}_{{\text {eff}}}^{w*}\dot{\mathbf {u}}_0^u + \frac{{{S_v}}}{{{m^{\textit{w}}}}}{{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}{{{\mathbf {R}}}}'_c \right) . \end{aligned}$$
(35)

The zero-order response of the vehicle \({\mathbf {u}}_{0}^{u}\) appears in the RHS of Eq. (35) (Eq. (28)), but according to Eq. (32)  \({\mathbf {u}}_{0}^{u}={\mathbf {0}}\). Subsequently,  \({\mathbf {u}}_{0}^{u}\) vanishes from Eq. (35) and the bridge’s EOM remains uncoupled. Thus, the first-order response of the bridge  \({\mathbf {u}}_{1}^{B}\) includes also terms dependent on the impedance ratio \(C=2M{\varOmega }\zeta ^p\) (multiplying all terms of Eq. (35) with \(\varepsilon ={\varOmega }\)), but still ignores the vehicle’s response (Eq. (35)).

Similar to the bridge, the vehicle’s upper part first-order response (Eq. (29)) is:

$$\begin{aligned} \begin{aligned}&\frac{1}{{{m^B}}}{{{\mathbf {m}}}^u}{{\ddot{\mathbf {u}}}}_1^u + \frac{1}{{{m^B}{\omega ^B}}}{{{\mathbf {c}}}^u}\dot{\mathbf {u}}_1^u + \frac{1}{{{m^B}{{\left( {{\omega ^B}} \right) }^2}}}{{{\mathbf {k}}}^u}{{\mathbf {u}}}_1^u \\&\quad = - 2M{\zeta ^p}{\left( {{{{\mathbf {W}}}^*}} \right) ^{\text {T}}}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}\dot{\mathbf {u}}_0^B + {S_v}{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}{{\mathbf {u}}}_0^B + {S_v}{{{\mathbf {R}}}}'_c} \right) \end{aligned}\nonumber \\ \end{aligned}$$
(36)

dependent solely on the zero-order response of the bridge.

Again, for the special case of small normalized mass of the vehicle’s wheels \({{M}^{w}}\) (Eq. (33)), the first-order bridge’s EOM (Eq. (35)) simplifies further to:

$$\begin{aligned} \begin{aligned}&{{{\mathbf {M}}}^B}{{\ddot{\mathbf {u}}}}_1^B + {{{\mathbf {C}}}^B}\dot{\mathbf {u}}_1^B + {{{\mathbf {K}}}^B}{{\mathbf {u}}}_1^B \\&\quad = - 2M{\zeta ^p}{{{\mathbf {W}}}^B}\left( {{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}\dot{\mathbf {u}}_0^B + {S_v}{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}{{\mathbf {u}}}_0^B + {S_v}{{{\mathbf {R}}}}'_c} \right) . \end{aligned}\nonumber \\ \end{aligned}$$
(37)

This asymptotic expansion analysis of the coupled VBI problem shows that the response of the bridge up to first order in \(\varepsilon \) does not depend on the response of the vehicle. In particular, “Appendix C” confirms that the response of the vehicle has a second-order effect on the vibration of the bridge [34].

To demonstrate the effect of different orders of \(\varepsilon \) on bridge response, Fig. 3 illustrates the zero-order (Eq. (31)) and first-order (Eq. (35)) response of the bridge, versus the bridge response from the complete coupled solution (Eq. (28)) of the vehicle–bridge system of Sect. 5.1. Specifically, the VBI system consists of a Pioneer passenger train [35] traversing the simply supported Skidträsk bridge in Sweden [24], with the properties of both subsystems given in Sect. 5.1. Note that all solutions take into account the wheels’ mass \({{M}^{w}}\), as this is not negligible. As expected, smaller orders of the bridge response (e.g., zero order) have a higher effect on the total response of the bridge, compared to higher orders (e.g., first order) (Fig. 3a, c). In addition, the first two orders of the bridge response (\(z_0^B + \varepsilon z_1^B\)) provide a very good approximation of the response of the bridge from the coupled solution (Fig. 3b, d).

Fig. 3
figure 3

Dimensionless response of the midpoint of the Skidträsk bridge [24] traversed by an one-vehicle Pioneer passenger train [35]: a zero-order \(z_0^B\) and first-order \(\varepsilon z_1^B\) displacements, and b sum of the first two orders \(z_0^B + \varepsilon z_1^B\), versus the coupled solution displacement; c zero-order \({\ddot{z}}_0^B\) and first-order \(\varepsilon {\ddot{z}}_1^B\) accelerations, and d sum of the first two orders \({\ddot{z}}_0^B + \varepsilon {\ddot{z}}_1^B\), versus the coupled solution acceleration

Full size image

4.2 Extended Modified Bridge System (EMBS) method

The asymptotic expansion analysis of Sect. 4.1 about the small dimensionless parameter \(\varepsilon ={\varOmega }\) reveals the terms that should be included in the EOM of the bridge to consider at least all terms up to first order in \(\varepsilon \). This allows to eliminate the vehicle response from the EOM of the bridge (Eq. (19)).

In particular, Eq. (31) shows that the only parameters of the vehicle that affect the zero-order response of the bridge \({\mathbf {u}}_{0}^{B}\) are the vehicle’s mass (through  \({{{\mathbf {F}}}^{B}}\) and \({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\)) and moving speed (through \(S_v\)). The dynamic characteristics of the primary suspension system of the vehicle (stiffness  \({{K}}=M{{{\varOmega } }^{2}}\) and impedance \({{C}}=2M{\varOmega } {{\zeta }^{P}}\) ratios) do not appear in the bridge’s zero-order EOM (Eq. (31)), as both are related to the small perturbation parameter \(\varepsilon = {\varOmega }\). (Both are ratios of higher \(\varepsilon \) orders.)

The first-order response of the bridge \({\mathbf {u}}_{1}^{B}\) additionally considers the impedance ratio C of the primary suspension system of the vehicle. Note that the impedance ratio  C is not negligible, especially for railway bridges traversed by locomotives [26]. On the other hand, the stiffness ratio of the vehicle \({{K}}=M{{{\varOmega } }^{2}}\) still does not affect the first-order EOM of the bridge (Eq. (35)) as this is of second order in  \(\varepsilon \): \(\varepsilon ^2 ={\varOmega } ^2\). More importantly,  \({\mathbf {u}}_{1}^{B}\) does not depend on the vehicle response; thus, the first-order EOM of the bridge remains uncoupled (Eq. (35)). Qualitatively, these findings are in accordance with the conclusions derived by the analytical examination of a simple SDOF vehicle–SDOF bridge system [21].

Based on the expressions of the zero- and first-order response of the bridge (Eqs. (31) and (35)), and neglecting higher-order terms with minor influence on the bridge response, this section proposes a decoupled MDOF EOM for the bridge system. The proposed formula depends on the self-weight of the vehicle \({{{\mathbf {F}}}^{B}}\), the impedance ratio of the vehicle’s primary suspension system C, the normalized mass of the wheels \(M_w\) and the speed parameter  \(S_v\) (Eqs. (31) and (35)), while it neglects terms associated with the stiffness ratio K and vehicle’s response  \({{{{\mathbf {u}}}}^u}\) and \({{\dot{\mathbf {u}}}^u}\):

$$\begin{aligned}&{{{\mathbf {M}}}^B}{{{{\ddot{\mathbf {u}}}}}^B} + \left( {{{{\mathbf {C}}}^B} + {{{\mathbf {C}}}_{{\text {EMBS}}}}} \right) {{\dot{\mathbf {u}}}^B} + \left( {{{{\mathbf {K}}}^B} + {{{\mathbf {K}}}_{{\text {EMBS}}}}} \right) {{{\mathbf {u}}}^B}\nonumber \\&\quad = {{{\mathbf {F}}}^B} + {{{\mathbf {F}}}_{{\text {EMBS}}}}. \end{aligned}$$
(38)

In this decoupled bridge EOM (Eq. (38)),  \({{{\mathbf {C}}}_{\text {EMBS}}}\) is the additional damping matrix:

$$\begin{aligned} {{{\mathbf {C}}}_{\text {EMBS}}}={{C}}{\mathbf {W}}_{\text {eff}}^{w} +2{{S}_{v}}{{{\mathbf {W}}_{\text {eff}}^{B,d}}} - \frac{1}{{{\omega }^{B}}}{\mathbf {W}}_{\text {eff}}^{B}{{\left( {{{\mathbf {m}}}^{B}} \right) }^{-1}}{{{\mathbf {c}}}^{B}},\nonumber \\ \end{aligned}$$
(39)

\({{{\mathbf {K}}}_{\text {EMBS}}}\) is the additional stiffness matrix:

$$\begin{aligned} {{{\mathbf {K}}}_{{\text {EMBS}}}}&= C{S_v}{{\mathbf {W}}}_{{\text {eff}}}^{w,d} + S_v^2{{\mathbf {W}}}_{{\text {eff}}}^{B,dd}\nonumber \\&\quad - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {k}}}^B} , \end{aligned}$$
(40)

and \({{{\mathbf {F}}}_{\text {EMBS}}}\) is the uncoupled additional loading vector:

$$\begin{aligned} {{{\mathbf {F}}}_{{\text {EMBS}}}}&= - \frac{1}{{{{\left( {{\omega ^B}} \right) }^2}L}}{{\mathbf {W}}}_{{\text {eff}}}^B{\left( {{{{\mathbf {m}}}^B}} \right) ^{ - 1}}{{{\mathbf {f}}}^B} \nonumber \\&\quad - {{{\mathbf {W}}}^B}{{{\mathbf {G}}}^{ - 1}}\left( {\frac{{C{S_v}}}{{{m^{\textit{w}}}}}{{{\mathbf {R}}}}'_c + \frac{{S_v^2}}{{{m^B}}}{{{\mathbf {R}}}}''_c} \right) . \end{aligned}$$
(41)
Fig. 4
figure 4

Schematic representation of the a coupled VBI analysis, b Extended Modified Bridge System (EMBS) method and c moving load approximation

Full size image

The formulation of Eqs. (38) to (41) constitutes the Extended Modified Bridge System (EMBS) as it extends the previously developed MBS method for SDOF vehicle–SDOF bridge systems [21]. The EMBS method allows an MDOF description of the effects of VBI on the bridge system, via time-varying additional damping, stiffness and loading terms, which are independent of the vehicle response (Fig. 4b). All involved parameters are known a priori; thus, the calculation of the additional matrices does not require a response history analysis. As a result, the proposed approach is applicable to involved bridge configurations, where the consideration of higher modes is preferable, if not necessary. In addition, it allows the accurate estimation of the bridge acceleration, which typically requires a higher number of modes than the displacement, and constitutes an important SLS design consideration according to contemporary railway codes [14,15,16]. At the same time, the EMBS approach is simpler than the coupled VBI analysis (Fig. 4a), as it does not require the modeling of the vehicle system and coupled interaction, making it more practical for bridge design.

The EMBS gives the vehicle response by substituting the independently calculated bridge response into the vehicle’s EOM (Eq. (21)) (schematically illustrated in Fig. 4b). In other words, the response analysis remains uncoupled.

4.3 Decoupled analysis for small mass of the vehicle’s wheels \({{M}^{w}}\ll 1\)

When the normalized mass of the vehicle’s wheels is negligible (\({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\ll 1\)), Eqs. (39) to (41) simplify further to:

$$\begin{aligned}&{{{\mathbf {C}}}_{\text {I}}}\left( x \right) ={{C}}{{{\mathbf {W}}}^{B}}{{\left( {{{\mathbf {W}}}^{B}} \right) }^{\text {T}}}, \end{aligned}$$
(42)
$$\begin{aligned}&{{{\mathbf {K}}}_{\text {I}}} \left( x \right) ={{C}}{{S}_{v}}{{{\mathbf {W}}}^{B}}{{\left( {{{\mathbf {W}}}^{B}} \right) }}'^{\text {T}}, \end{aligned}$$
(43)

and

$$\begin{aligned} {{{\mathbf {F}}}_{\text {I}}}=-{{C}}{{S}_{v}}{{{\mathbf {W}}}^{B}}{{{\mathbf {R}}}}'_{c}. \end{aligned}$$
(44)

Consequently, the dimensionless, decoupled EOM of the bridge (Eq. (38)) becomes:

$$\begin{aligned} \begin{aligned}&{{{\mathbf {M}}}^B}{{{{\ddot{\mathbf {u}}}}}^B} + \left( {{{{\mathbf {C}}}^B} + C{{{\mathbf {W}}}^B}{{\left( {{{{\mathbf {W}}}^B}} \right) }^{\text {T}}}} \right) {{\dot{\mathbf {u}}}^B} \\&\quad + \left( {{{{\mathbf {K}}}^B} + C{S_v}{{{\mathbf {W}}}^B}{{\left( {{{{\mathbf {W}}}^B}} \right) }^\prime }^{\text {T}}} \right) {{{\mathbf {u}}}^B} = {{{\mathbf {F}}}^B} - C{S_v}{{{\mathbf {W}}}^B}{{{\mathbf {R}}}}'_c. \end{aligned} \end{aligned}$$
(45)

This approximation (Eq. (45)) relies on the assumption of both small stiffness ratio K and small normalized mass of the wheels \(M^{{w}}\).

5 EMBS to decouple the VBI problem: numerical examples

Different to most decoupling methods, which are mainly tailored to particular bridge types, e.g., simply supported bridges [14, 26], the proposed EMBS approach is applicable to a variety of MDOF vehicle–MDOF bridge configurations. This constitutes an extension of the previously developed MBS method [21]. In addition, unlike the MBS, the EMBS method enables the accurate approximation of the bridge deck acceleration. The present section demonstrates, via numerical applications, that the proposed scheme can accurately capture the effect of VBI on both displacement and acceleration of the sustaining bridge, outperforming existing decoupling methodologies. In all cases, the benchmark solution is that of the fully coupled system [11].

In the following examples, the solution of the vehicle–bridge system employs the complete finite element (FE) model of the bridge (as opposed to the modal superposition method that typically considers a reduced number of modes), except for the MBS method that considers solely the first mode of the bridge. The time integration follows the Newmark-beta method with \(\gamma ={1}/{2}\) and \(\beta ={1}/{4}\) [36].

5.1 A ten-vehicle Pioneer passenger train traversing a simply supported bridge

The first example considers the \(L=36\ {\text {m}}\) long, simply supported Skidträsk bridge [24] traversed by a ten-vehicle Pioneer passenger train [35] at speed \(v=250\ {\text {km}}/{\text {h}}\). The vehicle is simulated as a 2D multi-body assembly consisting of rigid bodies connected with linear spring and dashpots (Fig. 1). The bridge is modeled with ten 2D Euler–Bernoulli beams, using linear and cubic (Hermitian) shape functions [37]. The properties of both vehicle and bridge are taken from [21]. The study assumes “good” quality of irregularities according to the German spectra [29] (Fig. 2b). Figure 5 illustrates the response of the vehicle–bridge system from the solution of the coupled system (Eq. (19)), the proposed EMBS method (Eq. (38)), the MBS approach [21] and the moving load/virtual path method. The latter first solves the bridge system via the moving load approximation (Eq. (34)) and then substitutes the bridge response into the vehicle’s EOM to estimate the vehicle response [35]. Note that the ADM of Eurocode does not consider any additional damping, as the bridge is longer than 30 m [14]. Also, according to Eurocode an amplification factor \({\varphi }''=0.014\) [14] should be considered to account for the effect of irregularities on the response of the bridge (assuming no carefully maintained rails). In this case, \({\varphi }''\) is very small; hence, it is neglected. Thus, the solution of Eurocode coincides with the moving load approximation.

Fig. 5
figure 5

a Displacement and b acceleration histories of the midpoint of the Skidträsk bridge [24] under the passage of a ten-vehicle Pioneer passenger train [35], c zoom in of (b) between 2 and 3 s for the EMBS method and the coupled solution, and d acceleration history of the car body of the tenth vehicle. “Good” quality of irregularities according to the German spectra (Fig. 2b) [29] is considered. The maximum permitted bridge deck acceleration is \({{a}_{\max }} = 3.5\;{\text {m}}/{{{\text {s}}^{\text {2}}}}\) [14, 15]

Full size image

Other methods available in the literature to capture the effect of VBI on bridge response mainly focus on the favorable damping effect of VBI. A previous study by the authors [26] proposed a method to estimate the time-varying additional damping matrix because of VBI for a variety of bridges, as well as simplified formulas to estimate additional damping ratios for simply supported and continuous bridges. For the Skidträsk bridge traversed by a Pioneer passenger train, this additional damping approach [26] suggests an additional damping ratio \({{\zeta }_{\text {add}}}=0.76\%\). This method, although accurately estimates the favorable damping effect of VBI on bridge response, does not consider the additional stiffness effect and effect of irregularities, as opposed to the MBS and EMBS methods.

The most remarkable difference between the proposed EMBS method and the other three decoupling methodologies (i.e., the MBS, moving load and additional damping approaches) is that the EMBS method offers an excellent approximation of the bridge deck acceleration (Fig. 5b, c). More specifically, the proposed EMBS method is in very good agreement with the solution of the coupled system for both displacement and acceleration (at the midpoint) of the bridge (Fig. 5a–c). Contrarily, the MBS approach is in good agreement with the EMBS method and the coupled solution for the displacement of the bridge (Fig. 5a), but does not capture the acceleration (Fig. 5b), as this requires the consideration of higher modes of the bridge [38]. Also, the MBS method ignores the mass of the vehicle’s wheels, which also affects the bridge response. The additional damping approach [26] offers a good approximation of the bridge displacement (Fig. 5a), but underestimates the acceleration (Fig. 5b), as it does not account for the effect of irregularities. Hence, in cases where the bridge acceleration is of interest (e.g., for SLS checks [14,15,16]), the EMBS approach is preferable over the MBS and additional damping methods, even for simply supported bridges (Fig. 5b). The moving load approximation overestimates the bridge displacement (Fig. 5a) as it neglects the favorable damping effect of VBI. On the other hand, it considerably underestimates the acceleration of the bridge as it ignores the effect of irregularities (Fig. 5b). The results confirm that the effect of irregularities is more evident on the acceleration rather than the displacement of the bridge, which is in agreement with the study of Salcher et al. [27]. Figure 5c also shows the maximum permitted bridge deck acceleration according to Eurocode [14] and the Chinese Code for Design of High-Speed Railway [15], which, in both cases, is  \({{a}_{\max }}=3.5\;{\text {m}}/{{{\text {s}}^{\text {2}}}}\). The acceleration of the bridge satisfies this limitation for the assumed vehicle model, running speed and irregularities profile. Lastly, Fig. 5d illustrates the acceleration history of the car body of the tenth vehicle. The response of the vehicle is very close for all methods examined due to the dominating effect of irregularities [21], which is taken into account in the vehicle’s EOM in all cases (Eq. (21)).

5.2 A ten-vehicle Pioneer passenger train traversing a three-span continuous bridge

This section examines a three-span continuous bridge [39] traversed by a ten-vehicle Pioneer train [35] at speed \(v=255\ {\text {km}}/{\text {h}}\) (Fig. 6a). Each span is \(L=56\ {\text {m}}\) long, with mass per unit length \(m=11.69\ {\text {t}}/{\text {m}}\), Young’s modulus \(E=35.50\ \text {GPa}\) and flexural moment of inertia \(I=10.56\ {{\text {m}}^{4}}\). The bridge model consists of twenty 2D Euler–Bernoulli beams for each span, while the structural Rayleigh damping matrix results by considering damping ratio 2% for the first two modes. The quality of rail irregularities is “good” (Fig. 2b). For this bridge configuration, Eurocode considers neither additional damping (all spans are longer than 30 m) nor amplification of the response because of irregularities. (The determinant length is  \({{L}_{\varphi }}=62.1\ \text {m}>40\ \text {m}\) [14].)

Fig. 6
figure 6

a Three-span continuous bridge [39] traversed by a ten-vehicle Pioneer passenger train [35]: b displacement and c acceleration histories of the midpoint of the middle span of the bridge, and d acceleration history of the car body of the tenth vehicle, for “good” quality of irregularities according to the German spectra (Fig. 2b) [29]. The maximum permitted bridge deck acceleration is \({{a}_{\max }}=3.5\;{\text {m}}/{{{\text {s}}^{\text {2}}}}\) [14, 15]

Full size image

Figure 6 illustrates the response history at the midpoint of the middle span of the continuous bridge (Fig. 6b, c) and the acceleration history of the car body of the tenth vehicle (Fig. 6d). Specifically, it compares the response of the fully coupled vehicle–bridge system, with the EMBS, MBS, additional damping [26] and moving load/virtual path methods. For the additional damping approach, the additional damping ratio is \({{\zeta }_{\text {add,1}}}=2.44\%\) for the first mode and \({{\zeta }_{\text {add,2}}}=1.70\%\) for the second mode [26]. Similar to the simply supported bridge of Fig. 5, the proposed EMBS method is the only decoupling approach in excellent agreement with the coupled solution when it comes to the acceleration of the bridge. As expected, the MBS method, that only accounts for the bridge’s first mode, does not accurately return the bridge response (Fig. 6b, c). The additional damping approach [26] adequately estimates the bridge displacement (Fig. 6b), but does not capture the acceleration (Fig. 6c), as it neglects the effect of irregularities. Again, the moving load approximation overestimates the displacement of the bridge (Fig. 6b), while it underestimates the corresponding acceleration (Fig. 6c). The acceleration of the vehicle is identical for all methods examined (Fig. 6d), despite the inability of the MBS method to adequately return the continuous bridge’s displacement (Fig. 6b), due to the strong effect of irregularities.

5.3 A ten-vehicle Pioneer passenger train traversing an arch bridge

The arch bridge of Fig. 7a is also traversed by a ten-vehicle Pioneer train. The bridge is 142.5 m long, 16 m wide and 30 m high and is derived from the study of Zeng et al. [12]. It consists of parabolic arch ribs, main girders, struts, cross-beams, stringers, suspenders and a concrete deck, each of which modeled with different FEs. The arch ribs, main girders, struts, cross-beams and stringers are simulated with three-dimensional (3D) Euler–Bernoulli beams [12], with linear shape functions for the axial (longitudinal) and torsional DOFs and cubic (Hermitian) shape functions for the flexural DOFs [37]. The suspenders are simulated with two-node uniaxial link elements with three translational DOFs per node, and the bridge deck is modeled with elastic four-node axisymmetric quadrilateral shell elements [12]. For the shell elements, second-order shape functions describe the in-plane translations and fourth-order shape functions the out-of-plane DOFs [12]. Rigid beam elements connect the concrete deck (shell elements) with the main girders and cross-beams (3D Euler–Bernoulli beams) [12]. The first bending frequency of the bridge is \({{f}^{B}}=2.04\ \text {Hz}\), and the Rayleigh damping matrix results by considering damping ratio 2.0% for the first two modes. The vehicle is modeled as a 3D multi-body assembly [12]. The train runs on rails of “good” quality of irregularities (Fig. 2a) at speed \(v=180\ {\text {km}}/{\text {h}}\).

Fig. 7
figure 7

a Arch bridge traversed by a ten-vehicle Pioneer passenger train [12]: b displacement, c torsion and d acceleration histories of the “examined point” of (a), and e acceleration history of the car body of the tenth vehicle, for “good” quality of irregularities according to the German spectra (Fig. 2b) [29]. The maximum permitted bridge deck acceleration, according to Eurocode, is  \({{a}_{\max }}=3.5\;{\text {m}}/{{{\text {s}}^{\text {2}}}}\) [14, 15]

Full size image
Fig. 8
figure 8

a–c Displacement and d–f acceleration histories at the midpoint of the simply supported bridge of Fig. 5a, d, at the midpoint of the middle span of the continuous bridge of Fig. 6b, e, and at the “examined point” of the arch bridge of Fig. 7c, f, for small normalized mass of the train’s wheels (\({{M}^{w}}={{{m}^{w}}}/{{{m}^{B}}}\ll 1\))

Full size image

Figure 7b–d illustrates the displacement \({\tilde{z}}^B\), torsion \({\tilde{\phi }}^B\) and acceleration \({\ddot{\tilde{z}}}^{B}\) histories of the “examined point” of the bridge according to Fig. 7a. The EMBS method is, once again, in perfect agreement with the solution of the coupled VBI system [12]. The MBS approach only accounts for the first vertical mode of the arch bridge and hence considerably underestimates the displacement and acceleration (Fig. 7b, d), while, as expected, it returns zero torsion of the bridge deck (Fig. 7c). For such a complicated bridge model, the additional damping approach considers a time-varying additional damping matrix [26]. However, it neglects the effect of irregularities; thus, in this case, it underestimates both displacement and acceleration of the bridge deck (Fig. 7b–d). The response of the bridge according to the moving load approximation is similar to that from the additional damping approach (Fig. 7b–d). Lastly, Eurocode considers a determinant length \({{L}_{\varphi }}={L}/{2}=71.25\ \text {m}\) for the arch bridge [14]. Consequently, the amplification factor to take into account the effect of irregularities is \({\varphi }''=0\) [14], and the solution of Eurocode coincides with the moving load approximation. This example shows that the EMBS method accurately predicts the bridge response even for complicated bridge configurations, as the proposed formula (Eqs. (38) to (41)) is generic and does not depend on the assumed bridge model. Finally, the vehicle acceleration from the coupled solution, the EMBS approach and the virtual path method [35] is the same (Fig. 7e). Contrarily, the MBS approach, that does not adequately estimate the bridge response, underestimates the vehicle acceleration, despite the strong effect of irregularities (Fig. 7e).

In summary, comparing the response of the simply supported (Fig. 5a, b), continuous (Fig. 6b, c) and arch bridges (Fig. 7b–d) examined, under the passage of the same train and for the same irregularities profile, it becomes evident that the effect of irregularities varies for different types of bridges. In all cases, the acceleration of the bridge from the coupled solution and the EMBS method is larger compared to that from the moving load approximation and the additional damping approach [26] (Figs. 5b, 6c, 7d). This is attributed to the strong effect of irregularities on the acceleration of the bridge, which the last two methods neglect. Irregularities contain high-frequency components that trigger higher bridge modes, which should be taken into account when estimating the acceleration of even simple bridge configurations, such as simply supported bridges [38]. However, this is not the case for the bridge displacement. Although the moving load approximation still underestimates the displacement of the arch bridge (Fig. 7b), it overestimates the displacement of the simply supported and continuous bridges (Figs. 5a, 6b). This stems from the fact that, different to acceleration, the estimation of displacement of simple bridges (e.g., simply supported and continuous) typically requires the consideration of the first few modes [38]. The high-frequency components of irregularities do not affect these low-frequency modes. Contrarily, the additional damping effect of VBI is prominent for such modes [26] and hence significantly affects the displacement of simple bridges (Figs. 5a, 6b). This is also confirmed by the fact that the additional damping approach [26] adequately captures the displacement of both simply supported and continuous bridges (Figs. 5a, 6b). On the other hand, for more involved bridge models, such as the considered arch bridge, higher modes are necessary to accurately predict their displacement (Fig. 7b, c); thus, the effect of irregularities becomes evident in their displacement histories as well (Fig. 7b).

5.4 Decoupled analysis for small normalized mass of the vehicle’s wheels \({{M}^{w}}\ll 1\)

This section brings forward the important effect of wheels’ mass on vehicle–bridge coupling, which, to the best of our knowledge, has not received the attention it deserves in VBI literature. Therefore, unlike Figs. 5, 6 and 7, Fig. 8 illustrates the displacement and acceleration of the previously examined simply supported (Fig. 5), continuous (Fig. 6) and arch bridges (Fig. 7) (Sects. 5.1, 5.2 and 5.3) assuming small normalized mass of the vehicle’s wheels \({{M}^{w}}\ll 1\) (Eq. (45)). Specifically, it shows the response of the bridges from the solution of the coupled system and the proposed EMBS method (Eqs. (38) to (41)), which both take into account the mass of the wheels, and from the decoupled formula of Eq. (45) and the moving load approximation, which both ignore the wheels’ mass. The bridge displacement histories from the decoupled solution assuming small normalized mass of the vehicle’s wheels (Eq. (45)) are close to that from the coupled solution and the EMBS method (Fig. 8a–c). Larger discrepancies appear in the displacement history of the arch bridge (Fig. 8c), but still the decoupled solution of Eq. (45) returns more accurate results compared to the moving load approximation. Thus, when the bridge displacement is of interest, Eq. (45) can give a good estimation, mainly for simple bridge configurations (i.e., simply supported and continuous bridges).

On the other hand, the wheels’ mass appears to have a great impact on bridge acceleration. The decoupled bridge EOM that ignores the mass of the wheels (Eq. (45)) does not adequately estimate the bridge acceleration for any of the examined bridges (Fig. 8d–f). On the contrary, it significantly underestimates the acceleration, which is close to that from the moving load approximation. Thus, when the bridge acceleration is of interest, the decoupled EMBS method is more appropriate, as it is in excellent agreement with the coupled solution (Fig. 8d–f).

6 Conclusions

This study examines analytically an MDOF vehicle–MDOF bridge configuration and proposes a methodology to decouple the vehicle–bridge system. This analytical examination allows an MDOF description of the VBI effects on the response of the bridge and breaks down VBI into an additional stiffness matrix, an additional damping matrix and an additional loading vector. These three constituent VBI mechanisms depend on the dynamic characteristics of both vehicle and bridge, while the vehicle response appears solely in the addition loading term.

An asymptotic expansion analysis of the coupled system response, with respect to a small dimensionless parameter \(\varepsilon \), reveals the major coupling parameters between vehicles and bridges for different orders of the bridge response (e.g., zero and first order in \(\varepsilon \)). This parameter corresponds to the ratio \(\varepsilon = {\varOmega }\) of the frequency of the vehicle’s primary suspension system and the bridge’s fundamental frequency, which for practical train–bridge systems obtains small values. The zero-order response of the bridge depends on the normalized self-weight of the vehicle \({{{\mathbf {F}}}^{B}}\), the normalized mass of the wheels \(M^{{w}}\) and the speed parameter \(S_v\). At the same time, it is independent of the stiffness K and impedance  C ratios of the vehicle’s primary suspension system. The well-known moving load approximation constitutes a special case of the zero-order response of the bridge, under the additional assumption of small normalized mass of the wheels. Compared to the zero-order response, the first-order bridge response considers also coupling effects associated with the impedance ratio C, while also ignores coupling terms related to the stiffness ratio K. More importantly, the first-order response of the bridge is independent of the vehicle response, as the vehicle has a second-order effect on the vibration of the bridge. The latter is in agreement with previous studies.

In between the coupled solution (which considers the higher order effects of the vehicle response) and the moving load approximation (which completely neglects VBI), the study proposes the decoupling Extended Modified Bridge System (EMBS) method. This method stems from the zero- and first-order response of the bridge, which, according to the asymptotic expansion analysis, are independent of the stiffness ratio and vehicle response. Unlike the formerly developed MBS method, the proposed approach accounts for MDOF vehicle and MDOF bridge models. As a result, the EMBS method is applicable to a wide variety of bridges, including simply supported, continuous and arch bridges, and, at the same time, it accurately estimates the bridge deck acceleration. The latter constitutes an important SLS criterion in railway bridges according to current regulations [14,15,16]. Numerical applications on different bridge types indicate that the proposed approach is equally accurate with the coupled solution, while it outperforms existing decoupling methodologies (e.g., the moving load method). In addition, it is simpler than the solution of the fully coupled system, as it does not require the modelling of the vehicle and the interaction between the two subsystems. Subsequently, the proposed EMBS method can be particularly useful in bridge design practice.

Lastly, the study brings forward the effect of irregularities and wheels’ mass on bridge response. It shows that irregularities amplify the bridge acceleration for any bridge type, as well as the displacement of involved bridge configurations, such as arch bridges. On the other hand, the displacement of simple bridge systems, such as simply supported and continuous bridges, appears to be mainly affected by the additional damping effect of VBI, which is more prominent for lower bridge modes. The mass of the wheels primarily affects the acceleration of bridges. Neglecting the mass of the wheels leads to considerable underestimation of bridge acceleration. Contrarily, it does not affect significantly the estimation of displacement, especially for simple bridges (e.g., simply supported and continuous).