Stabilization of the passive walking dynamics of the compass-gait biped robot by developing the analytical expression of the controlled Poincaré map

Abstract

The compass-gait biped robot is a two-DoF legged mechanical system that has been known by its passive dynamic walking. This kind of passive biped robot is modeled by an impulsive hybrid nonlinear system that exhibits complex behaviors. This paper is concerned with the stabilization of the passive dynamic walking of the compass-gait biped robot by designing an analytical expression of the controlled Poincaré map. The suggested analytical method starts with the time-piecewise linearization of the impulsive system augmented with the controller, around a desired one-periodic passive hybrid limit cycle. By virtue of the first-order Taylor series, we design an explicit expression of the controlled Poincaré map. We present also a simplified expression of the controlled Poincaré map having a reduced dimension. In order to accomplish our goal concerned with the stabilization of the passive walking dynamics of the compass-gait biped robot, we develop first the linearized Poincaré map around the period-1 fixed point of the Poincaré map and we adopt a state-feedback control law to stabilize it. Furthermore, in order to enhance the effectiveness and robustness of the stabilization process, we adopt an LMI-based optimization approach by considering the controlled Poincaré map to design the feedback gain. In the end of this work, we provide some numerical and graphical simulation results, to show the validity of the designed control law by means of the controlled Poincaré map in the stabilization of the passive dynamic walking of the compass-gait biped robot.

Appendix A

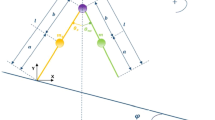
The PDW of the compass-gait biped robot consists of a continuous dynamics modeling the motion during the swing phase and an algebraic/discrete equation describing the instantaneous transition in the state vector during the impact phase [64].

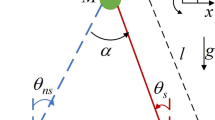
Let us consider the vector $\varvec{\theta }=\left[ \begin{array}{cc} \theta _{ns}&\,\theta _{s} \end{array} \right] ^T$ of generalized coordinates of the compass-gait biped robot. Then, the swing motion is defined by the following dynamics:

$$\begin{aligned} \varvec{{\mathcal {J}}}(\varvec{\theta })\ddot{\varvec{\theta }}+\varvec{{\mathcal {H}}}(\varvec{\theta },\dot{\varvec{\theta }})+\varvec{{\mathcal {G}}}(\varvec{\theta })=\varvec{{\mathcal {B}}}u \end{aligned}$$

(A-1)

where $\varvec{{\mathcal {J}}}$ is the inertia matrix, $\varvec{{\mathcal {H}}}$ includes Coriolis and centrifugal terms, $\varvec{{\mathcal {G}}}$ is the gravitational matrix/vector and $\varvec{{\mathcal {B}}}$ is the input matrix. These matrices are defined as follows:

${\varvec{{\mathcal {J}}}}(\varvec{\theta }) = \left[ \begin{array}{cc} mb^2 &{} -mlb\cos (\theta _{s}-\theta _{ns})\\ -mlb\cos (\theta _{s}-\theta _{ns}) \,\,\,\,\, &{} m_{H}l^2+m(l^2+a^2) \end{array} \right]$,

$\varvec{{{\mathcal {H}}}}(\varvec{\theta },\varvec{{\dot{\theta }}}) = \left[ \begin{array}{c} mlb{\dot{\theta }}_{s}^2\sin (\theta _{s}-\theta _{ns})\\ -mlb{\dot{\theta }}_{ns}^2\sin (\theta _{s}-\theta _{ns}) \end{array} \right]$,

$\varvec{{{\mathcal {G}}}}(\varvec{\theta }) = g\left[ \begin{array}{c} mbsin(\theta _{ns})\\ -(m_{H}l+m(a+l))\sin (\theta _{s}) \end{array} \right]$ and $\varvec{{{\mathcal {B}}}} = \left[ \begin{array}{c} -1\\ 1 \end{array} \right]$.

While descending the inclined walking surface of slope $\varphi$, the swing leg of the compass-gait biped robot is above the ground. Such situation is reformulated by the following set:

$$\begin{aligned} \varOmega =\left\{ \varvec{\theta }\in \mathfrak {R}^2\ :\ {{\mathcal {L}}}_{1}(\varvec{\theta })=l\left( \cos (\theta _{s}+\varphi )-\cos (\theta _{ns}+\varphi )\right) >0\right\} \end{aligned}$$

(A-2)

In addition, the impact phase happens if and only if the following conditions hold:

• 1. the swing leg reaches the walking surface,

• 2. the swing leg is moving downward,

• 3. the swing leg is in front of the stance leg.

These three impact conditions are recast by the following set:

$$\begin{aligned} \varGamma =\left\{ \begin{array}{rl} {{\mathcal {L}}}_{1}(\varvec{\theta }) &{}= l\left( \cos (\theta _{s}+\varphi )-\cos (\theta _{ns}+\varphi )\right) =0\\ {{\mathcal {L}}}_{2}(\varvec{\theta },\dot{\varvec{\theta }}) &{}= \frac{\partial \varPhi _{1}\left( \varvec{\theta }\right) }{\partial \varvec{\theta }} \dot{\varvec{\theta }}<0\\ {{\mathcal {L}}}_{3}(\varvec{\theta }) &{}= l\left( \sin (\theta _{ns})-\sin (\theta _{s})\right) >0 \end{array} \right\} \end{aligned}$$

(A-3)

At the impact phase, and then when the swing leg of the compass-gait biped robot encounters the walking surface, the vector of angular positions $\varvec{\theta }$ and the vector of angular velocities $\dot{\varvec{\theta }}$ undergo an instantaneous transition with respect to the two following algebraic expressions:

$$\begin{aligned}&\varvec{\theta }^{+}=\varvec{{{\mathcal {R}}}_{e}}\varvec{\theta }^{-} \end{aligned}$$

(A-4a)

$$\begin{aligned}&\dot{\varvec{\theta }}^{+}=\varvec{{{\mathcal {S}}}_{e}}\left( \varvec{\theta }^{-}\right) \dot{\varvec{\theta }}^{-} \end{aligned}$$

(A-4b)

where in (A-4), superscribes $^{+}$ and $^{-}$ denote, respectively, just after and just before the impact phase. The two matrices $\varvec{{{\mathcal {R}}}_{e}}$ and $\varvec{{{\mathcal {S}}}_{e}}\left( \varvec{\theta }^{-}\right)$ are expressed as follows: $\varvec{{{\mathcal {R}}}_{e}} {=} \left[ \begin{array}{cc} 0 &{}\ \ 1\\ 1 &{}\ \ 0 \end{array} \right]$, $\varvec{{{\mathcal {S}}}_{e}}\left( \varvec{\theta }^{-}\right) {=} {\varvec{Q}}_{p}^{-1}(\alpha )\,{\varvec{Q}}_{m}(\alpha )$, with

${\varvec{Q}}_{m}(\alpha ) {=} \left[ \begin{array}{cc} -mab \,\,\,\,\,&{} -mab{+}(m_{H}l^2{+}2mal)\cos (2\alpha )\\ 0 &{} -mab \end{array} \right]$,

${\varvec{Q}}_{p}(\alpha ) {=} \left[ \begin{array}{cc} mb(b-l\cos (2\alpha )) \,\,\,\,\, &{} \begin{array}{c}ml(l-b\cos (2\alpha ))+\\ ma^2{+}m_{H}l^2\end{array} \\ mb^2 &{} -mbl\cos (2\alpha ) \end{array} \right]$ Recall that $\alpha$ is the half-interleg angle and is given as $\alpha =\frac{1}{2}(\theta _{s}-\theta _{ns})$.

Hence, the continuous dynamics (A-1) and its constraint (A-2) and the algebraic equations in (A-4) and the set of impact conditions in (A-3) define the IHNLD of the compass-gait biped robot. It can be rewritten under the state representation in (1), where ${\varvec{f}}({\varvec{x}})=\left[ \begin{array}{c} \dot{\varvec{\theta }} \\ -\varvec{{{\mathcal {J}}}}(\varvec{\theta })^{-1}\left( \varvec{{{\mathcal {H}}}}(\varvec{\theta },\dot{\varvec{\theta }})+\varvec{{{\mathcal {G}}}}(\varvec{\theta })\right) \end{array} \right]$, ${\varvec{g}}({\varvec{x}})=\left[ \begin{array}{c} \varvec{{\mathcal {O}}}_{2 \times 1} \\ \varvec{{{\mathcal {J}}}}(\varvec{\theta })^{-1}\varvec{{{\mathcal {B}}}} \end{array} \right]$, ${{\varvec{h}}}\left( {\varvec{x}}\right) =\left[ \begin{array}{cc} \varvec{{{\mathcal {R}}}}_{e} &{}\, \varvec{{\mathcal {O}}}_{2\times 2}\\ \varvec{{\mathcal {O}}}_{2\times 2} &{}\, \varvec{{{\mathcal {S}}}}_{e}\left( \varvec{\theta }^{-}\right) \end{array} \right] {\varvec{x}}$, with $\varvec{{\mathcal {O}}}$ the zero matrix.