An improved quasi-zero stiffness vibration isolation system utilizing dry friction damping

Abstract

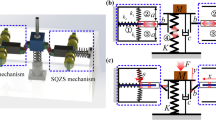
Quasi-zero stiffness (QZS) isolators, a nonlinear vibration isolation technique, enhance the isolation performance, by lowering the natural frequencies of an isolation system while providing higher static load bearing capacity compared to similarly performing linear isolators. Despite its performance improvement, the challenge of implementing QZS isolation systems is due to their highly nonlinear stiffness characteristics as a result of cubic like behavior of stiffness elements used. Although increasing linear damping in the isolation alleviates the input dependency of the QZS isolation systems by reducing the resonance amplitudes, it results in increased transmissibility in the isolation region, which is an adverse effect. Therefore, in this study, in order to overcome this, dry friction damping is implemented on the QZS isolation system. Hysteresis loop for the new QZS dry friction element is obtained and a mathematical model is introduced. For the nonlinear isolation system, harmonic balance method is used to transform the nonlinear differential equations into a set of nonlinear algebraic equations. For single harmonic motion, analytical expressions of Fourier coefficients are obtained in terms of elliptic integrals. Numerical solution of the resulting set of nonlinear algebraic equations is obtained via Newton’s method with arc-length continuation. Performance of the isolation system under periodic base excitation is studied for different base excitation levels and the stability of the periodic steady-state solutions is investigated.

Appendix

$$ f_{\text{ns}} = S_{1} + \frac{{2k_{h} L_{o} }}{\pi X}\left( {\frac{{S_{2} }}{{S_{3} \cos \left( {\psi_{1} } \right)}} - S_{4} E\left[ {\phi ,k} \right] - \frac{{{\mathbf{j}}2aX}}{{S_{4} }}F\left[ {\phi ,k} \right]} \right) $$

$$ f_{\text{nc}} = \frac{{2\mu N\left( { \sin \left( {\psi_{1} } \right) + 1} \right)}}{\pi } $$

where

$$ \begin{aligned} S_{1} & = {{\left( {X\left( {k_{h} + k_{v} } \right)\left( {\cos \psi_{1} + \psi_{1} - \pi /2} \right) - 2\mu N\cos \left( {\psi_{1} } \right)} \right)} \mathord{\left/ {\vphantom {{\left[ {X\left( {k_{h} + k_{v} } \right)\left( {\cos \psi_{1} + \psi_{1} - \pi /2} \right) - 2\mu N\cos \left( {\psi_{1} } \right)} \right]} \pi }} \right. \kern-0pt} \pi }, \\ S_{2} & = 2X^{2} - 6Xw_{0} + 4w_{0}^{2} + \left( {1 - \sin \left( {\psi_{1} } \right)} \right)\left( {a^{2} + w_{0}^{2} } \right) \\ S_{3} & = \sqrt {\left( {X - w_{0} } \right)^{2} + a^{2} } , \\ S_{4} & = \sqrt {\left( {X - ja} \right)^{2} - w0^{2} } \\ \end{aligned} $$

$\begin{aligned} \phi & = \frac{1}{{\cos \psi_{1} }}\sqrt {\frac{{\left( {X - ja} \right)^{2} - w_{0}^{2} }}{{\left( {X - w_{0} } \right)^{2} + a^{2} }}} \left( {\sin \psi_{1} - 1} \right), \\ k & = \sqrt {\frac{{\left( {X + ja} \right)^{2} - w_{0}^{2} }}{{\left( {X - ja} \right)^{2} - w_{0}^{2} }}} ,\,\,\,\,\,j = \sqrt { - 1} . \\ \end{aligned}$.

Incomplete first and second kind Elliptic integrals are defined as

$$ \begin{aligned} E\left[ {\alpha ,\beta } \right] & = \int\limits_{0}^{\alpha } {\frac{{\sqrt {1 - \beta^{2} t^{2} } }}{{\sqrt {1 - t^{2} } }}{\text{d}}t} \\ F\left[ {\alpha ,\beta } \right] & = \int\limits_{0}^{\alpha } {\frac{1}{{\sqrt {1 - t^{2} } \sqrt {1 - t^{2} \beta^{2} } }}{\text{d}}t} \\ K\left[ k \right] & = \int\limits_{0}^{1} {\frac{1}{{\sqrt {1 - t^{2} } \sqrt {1 - t^{2} k^{2} } }}{\text{d}}t} \\ \end{aligned} $$