Crinkled changes of variables for maps on a circle

Abstract

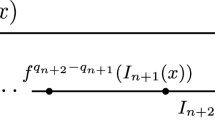
Take a piece of paper, crush it into a ball, and pound it flat onto a surface. The map from the original piece of paper to the surface is a non smooth change of variables $\varPhi$. It maps many points to the same point. This is what we mean by a “crinkled” map. Except that we work in one dimension, not two. Such crinkled change of variables occur naturally in many dynamical systems. One of the simplest dynamical systems with complicated dynamics is $z_{n+1}= 2\cdot z_n \bmod 1$. A general nonlinear map on the circle such as $x_{n+1}= 2\cdot x_n +\sin (2\pi x_n) \bmod 1$ has more complicated dynamics; in particular it has many more period N orbits for all $N>1$. We show there is a continuous change of variables function $z =\varPhi (x)$ that maps the circle onto itself. By $z_n =\varPhi (x_n)$, it converts the x trajectories into the simpler system $z_{n+1}= m\cdot z_n \bmod 1$. This $\varPhi$ serves as a change of variables, which in many cases will be shown to be non monotonic and nowhere differentiable. Our goal is to explain this sophisticated theory which is little known outside the technical dynamics literature. We hope that our examples and proofs will give the reader a better understanding of the outcomes of changes of variables.