Long-term evolution of mid-altitude quasi-satellite orbits

Abstract

Quasi-satellite orbits are of great interest for the exploration of planetary moons because of their dynamical features and close proximity with respect to the surface of scientifically relevant objects like Phobos and Deimos. This paper explores the equations of the elliptical Hill problem, offering a new analytical insight into the long-term evolution of mid-altitude quasi-satellite orbits. Our developments are based on the Yamanaka–Ankersen solution of the Tschauner–Hempel equations and capture the effects of the secondary’s gravity and orbital eccentricity on the shape and orientation of near-equatorial retrograde relative trajectories. The analytical solution of the in-plane and out-of-plane components of the secular motion is achieved by averaging over the relative longitude of a spacecraft as seen from the co-rotating frame of the two primaries. Developments are validated against the numerical integration of quasi-periodic trajectories that densely cover the surface of three-dimensional invariant tori. This analysis confirms the stable nature of quasi-satellite orbits and provides new tools for future spacecraft missions such as the Martian Moons eXploration envisaged by JAXA.

1 Introduction

The study of retrograde relative trajectories around the secondary of two attracting masses has always been of interest to astronomers and orbital mechanicists since their original discovery in 1897 [1]. Already in 1913, Jackson was theorizing that this type of orbits may be more stable than direct trajectories [2], a result that was eventually confirmed by Hénon in his numerical investigations of the restricted three-body problem [3]. Based on the results of Hénon’s analysis, retrograde relative orbits, also known in the literature as distant retrograde or quasi-satellite orbits (QSO), have gained the attention of several space agencies and astrodynamics researchers looking for efficient trajectories to explore the solar system. Many spacecraft missions have recently been proposed to fly on retrograde relative orbits around planetary moons, including the Russian Phobos-Grunt, NASA’s ARM, and the European DePhine [4,5,6]. JAXA is also planning the Martian Moons eXploration mission (MMX) in order to finally settle the debate on the moons’ origin and further deepen our understanding of the Martian system. The spacecraft will be placed on quasi-satellite trajectories near the largest of the Martian moons Phobos, studying its dynamical and geophysical features for more then 3 years [7].

In order to better understand motion near small irregular moons and prepare for the proximity operations of MMX, this paper focuses on the design and long-term evolution of quasi-satellite orbits. Recent developments on this matter can be separated in numerical and analytical investigations of a point mass subject to the gravitational attraction of a massive primary and a much lighter secondary. In the case of numerical investigations, shooting techniques are typically applied to calculate periodic or quasi-periodic solutions in the vicinity of planetary satellites [8,9,10]. Once these particular solutions are obtained, stability analysis can be carried out using Floquet theory and/or chaos indicators [11,12,13,14]. As for analytical developments, disturbing functions and variational equations are typically averaged over the time scales of fast variables to obtain qualitative information on the system dynamics. Belonging to the first category are the contributions inspired by Mikkola and Innanen, who first considered quasi-satellite trajectories as slightly perturbed Keplerian orbits in a 1:1 mean motion resonance [15]. Building on this idea, Namouni, Brasser et al., and Mikkola et al. later found out that transitions between QSOs and other 1:1 resonant orbit types are not only possible but also frequent [16,17,18]. Necessary conditions for transitioning between different 1:1 orbital regimes were recently developed by Sidorenko et al. using Hamiltonian theory and double-averaging [19]. A second approach is to consider quasi-satellite orbits as perturbed relative trajectories that deviate from 2:1 ellipses because of the gravitational attraction of the secondary body. Starting from the equations of the circular restricted three-body problem (CRTBP), Kogan used linearization and averaging to prove the stability of QSO orbits when Phobos is in a circular orbit around Mars [20]. Lidov and Vashkov’yak extended this approach to the elliptical three-body problem, but failed to come up with an analytical solution that was valid in the orbital regime of the Martian moon [21]. Owing to small mass ratios and QSO altitudes, Lara more recently considered Lie–Deprit transformations within the framework of the planar circular Hill problem [22]. Differently from the CRTBP, the Hill problem does not depend on any external parameter and is the ideal laboratory for dynamical investigations of many planetary systems. Cabral recognized this advantage and included eccentricity and out-of-plane oscillations to increase the fidelity of his analytical developments [23]. Unfortunately, despite thorough derivations with the variation of parameters, the differential equations of QSO amplitudes, offsets, and phase angles do not seem to adequately capture the long-term evolution of point masses in this orbital regime.

In this paper, we investigate the long-term evolution of mid-altitude quasi-satellite orbits within the framework of the spatial elliptical Hill problem (EHP). Our developments are also based on the analytical solution of the Tschauner–Hempel equations derived by Yamanaka and Ankersen in [24], but yields different equations than the ones found in Cabral’s thesis. The analytical derivations are validated by comparison with the numerical integration of initial conditions on the surface of three-dimensional quasi-periodic invariant tori [25]. These invariant manifolds are obtained through the invariant tori of a stroboscopic mapping [26, 27] and well represent the equivalent of QSO orbits whenever eccentricity and cross-track oscillations are taken into account. Next, we average over one QSO period and derive a new set of equations of motion for the long-term evolution of satellites in this orbital regime. An analytical solution of these equations is then achieved. A near-identity transformation is implemented to accurately map averaged elements into their osculating counterpart. The solution is finally validated by comparison with the numerical integration of the osculating equations of motion.

The article is organized as follows. First, dynamical models and QSO are introduced in Sect. 2. A novel analytical solution for both the in-plane and out-of-plane components of motion is achieved in Sect. 3 after averaging the dynamical system over one orbital period. The near-identity transformation is presented in Sect. 4, along with the numerical validation of the analytical solution.

2 Dynamical models

Dynamical models and assumptions necessary for the analytical developments of Sect. 3 are hereby introduced. Starting from the equations of the elliptical restricted three-body problem (ERTBP), we linearize the dynamics in the vicinity of the secondary body and discuss validity regions for the equations of the EHP. Examples of quasi-satellite orbits are then illustrated along with their dynamical substitutes when the eccentricity of planetary moon is taken into account (Sect. 2.1). In Sect. 2.2, we momentarily neglect the gravitational attraction of the secondary body to overview the analytical solution of the unperturbed problem as developed by Yamanaka and Ankersen in [24]. We then introduce Gauss variational equations (GVEs) in Sect. 2.3 to discuss the effects of the moon’s gravity on the solution of the integrable problem. The results of this investigation are validated in Sect. 2.4 by comparison with the numerical integration of the EHP over 100 orbital revolutions (i.e., approximately one month in the Mars–Phobos system).

2.1 Elliptical Hill problem

Consider the motion of a massless satellite subject to the gravitational attraction of a moon and its host planet. As seen from the barycenter of the secondary body, the dynamics of the spacecraft is better expressed in a rotating reference frame $\mathcal {S}'$ centered on the moon and such that ${\hat{\varvec{x}}}$ is constantly aligned with the separatrix between the two primaries, ${\hat{\varvec{z}}}$ is parallel to the orbital angular momentum of the moon, and ${\hat{\varvec{y}}} = {\hat{\varvec{z}}} \times {\hat{\varvec{x}}}$ completes the right-handed triad. The equations of motion are given by the equations of ERTBP:

$$\begin{aligned} \ddot{\varvec{r}} + 2\,\left( \dfrac{\dot{\gamma }}{\gamma }\,I + [{\hat{\varvec{z}}}]\right) \,\dot{\varvec{r}} = \nabla \mathcal {U}(\varvec{r}), \end{aligned}$$

(1)

where dots denote differentiation with respect to the true anomaly of the planetary satellite, $\nu$; $\varvec{r}$ and $\dot{\varvec{r}}$ are the position and velocity components of the spacecraft in $\mathcal {S}'$, respectively; I is the identity matrix; $[{\hat{\varvec{z}}}]$ is a skew-symmetric matrix such that $[{\hat{\varvec{z}}}]\,\varvec{r} = {\hat{\varvec{z}}}\times \varvec{r}$; and

$$\begin{aligned} \mathcal {U}(\varvec{r})= & {} \dfrac{1}{\omega ^2}\,\left[ \dfrac{\mathcal {G}\,m}{r} + \dfrac{\mathcal {G}\,M}{r_1} + \dfrac{\mathcal {G}\,M}{r_{12}^3}\,\varvec{r}_{12}^T\,\varvec{r}\right] \nonumber \\&- \dfrac{1}{2}\,\varvec{r}^T\,\left( 2\,\dfrac{\dot{\gamma }}{\gamma }\,[{\hat{\varvec{z}}}] + [{\hat{\varvec{z}}}]\,[{\hat{\varvec{z}}}] \right) \,\varvec{r} \end{aligned}$$

(2)

is the effective potential, with $\mathcal {G}$, m, and M as the gravitational constant, mass of the secondary, and mass of the primary, respectively. Also note that

$$\begin{aligned} \omega = \sqrt{\mathcal {G}\,(M + m)}\,p^{-3/2}\,\gamma ^2 \end{aligned}$$

is the angular velocity of the rotating reference frame (along ${\hat{\varvec{z}}}$), whereas $\varvec{r}_{12} = \dfrac{p}{\gamma }\,{\hat{\varvec{x}}}$ is the relative position vector of the secondary as seen from the barycenter of the primary body. The variables $p = a\,(1-e^2)$ and $\gamma = (1 + e\,\cos {\nu })$ depend on the semimajor axis and eccentricity of the moon, hereby referred to as a and e. Finally, $r_{12} = \Vert \varvec{r}_{12}\Vert = p\,\gamma ^{-1}$ and $r_1 = \Vert \varvec{r}_1\Vert$, where $\varvec{r}_1 = \varvec{r} + \varvec{r}_{12}$ is the relative position vector of the spacecraft as seen from the barycenter of the primary.

It is assumed that the mass of the secondary is significantly smaller than the mass of the primary ($m/M<< 1$), as well as that the relative distance between the spacecraft and the secondary is much smaller than the distance between the two attractors ($r<< r_{12}$). Based on these assumptions, the term proportional to $r_1^{-1}$ in Eq. (2) can be expanded up to the second order in r to obtain

$$\begin{aligned}&\dfrac{\mathcal {G}\,M}{r_1} \simeq \dfrac{\mathcal {G}\,M}{r_{12}} - \dfrac{\mathcal {G}\,M}{r_{12}^3}\varvec{r}_{12}^T\,\varvec{r} + \dfrac{\mathcal {G}\,M}{2\,r_{12}^3}\,\varvec{r}^T\nonumber \\&\quad \left( -I + 3\,{\hat{\varvec{x}}}\,{\hat{\varvec{x}}}^T\right) \,\varvec{r} + \mathcal {O}(r^3). \end{aligned}$$

(3)

Moreover, since $\omega ^2 \simeq \mathcal {G}\,M\,p^{-3}\,\gamma ^4 = \mathcal {G}\,M\,\gamma \,r_{12}^{-3}$, the effective potential may be rewritten as

$$\begin{aligned}&\mathcal {V}(\varvec{r}) = \epsilon ^3\,\left( \dfrac{r_{12}^3}{\gamma \,r}\right) + \dfrac{r_{12}^2}{\gamma } + \dfrac{1}{2\,\gamma }\,\varvec{r}^T\,\left( -I + 3\,{\hat{\varvec{x}}}\,{\hat{\varvec{x}}}^T \right. \nonumber \\&\left. \quad +\, 2\,e\,\sin {\nu }\,[{\hat{\varvec{z}}}] - \gamma \,[{\hat{\varvec{z}}}]\,[{\hat{\varvec{z}}}]\right) \,\varvec{r}, \end{aligned}$$

(4)

where $\epsilon = (m/M)^{1/3}$ is the cubic root of the mass ratio parameter.

Figure 1 illustrates the logarithm of $|\mathcal {V} - \mathcal {U}|/\mathcal {U}$ for several three-body systems and mass ratio parameters when $e = 0$. Red contours mark the boundary of a region where the relative error between the three-body problem and the so-called Hill approximation of the effective potential is four orders of magnitude smaller than the absolute value of $\mathcal {U}$. As a result, the truncation errors can be considered negligible as long as $(m/M) < 10^{-4}$ and $r < 0.05\,a$.

Fig. 1

Relative error between the effective potential of the restricted three-body problem and its Hill approximation. Values are shown in logarithmic scale for different mass ratio parameters and three-body systems assuming $e = 0$. Axes are chosen to match 0.1a of the corresponding three-body system

Within the validity region of the Hill approximation, the equation of motion (1) can be further simplified by introducing pulsating coordinates $\varvec{r} = \epsilon \,p\,\gamma ^{-1}\,\tilde{\varvec{r}}$. This yields the first-order system of ordinary differential equations in $\nu$ known as the EHP [28]:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = u,\\ \dot{y} = v,\\ \dot{z} = w,\\ \dot{u} = \dfrac{1}{\gamma }\,\left( -\dfrac{x}{r^3} + 3\,x\right) \, + 2\,v,\\ \dot{v} = -\dfrac{y}{\gamma \,r^3}\, - 2\,u,\\ \dot{w} = -\dfrac{z}{\gamma \,r^3} - z. \end{array} \right. \end{aligned}$$

(5)

Here, x, y, z and u, v, w are the dimensionless position and velocity components of $\tilde{\varvec{r}}$ and $\dot{\tilde{\varvec{r}}} = \dfrac{\gamma }{\epsilon \,p}\,\left[ \dot{\varvec{r}} + \dfrac{\dot{\gamma }}{\gamma }\,\varvec{r}\right]$, respectively, whereas $\varvec{g} = -\dfrac{\tilde{\varvec{r}}}{\gamma \,\tilde{r}^3}$ stands for the gravitational attraction of the planetary moon in pulsating normalized units.

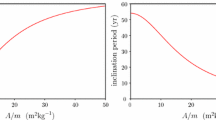
As it can be seen from Eq. (5), the EHP depends explicitly on the independent variable $\nu$ through $\gamma = (1 + e\,\cos {\nu })$. Because of this dependency, periodic orbits must be resonant with $2\,\pi$ and cannot be organized in families as in the circular case [29]. This change of paradigm is illustrated in the chart of Fig. 2, showing the orbital period of QSO of the Mars–Phobos system as a function of their positive x-axis crossing when $e = 0$. Among the infinite family members, only those whose period is resonant with 7.66 hrs—the orbital period of Phobos around Mars—survive when the eccentricity of Phobos, $e = 0.0151$, is taken into account (i.e., intersections with the horizontal lines of Fig. 2).

Fig. 2

Period vs positive x-crossing for the family of quasi-satellite orbits with $e = 0$. Only the periodic orbits whose period is resonant with $2\,\pi$ survive when $e \ne 0$

When the resonant condition is not met, periodic orbits are replaced by two-dimensional quasi-periodic invariant tori that belong to a family of quasi-periodic retrograde orbits [30]. To compute these manifolds, we adapt the numerical algorithm outlined in Gómez & Mondelo [26] and Olikara & Scheeres [27] and hereby referred to as “GMOS”. The main idea of GMOS is that quasi-periodic invariant tori can be calculated via invariant curves of a stroboscopic mapping by solving the boundary value problem described in [31]. The interested reader may find more details on the methodology in the authors’ original papers as well as in [31, 32]. In particular, Olikara provides an exhaustive explanation of the collocation method used in this work to march along the QSO family branch and generate a variety of quasi-periodic invariant tori with $e = 0.0151$ [32]. Several examples of planar quasi-periodic QSO orbits are shown in Fig. 3.

Fig. 3

Family members of the a QSO and b quasi-QSO orbit families

An advantage of the GMOS algorithm is that additional frequencies can be included to search for higher-dimensional solutions of Eq. (5). This feature was demonstrated by Baresi and Scheeres in [25] and is hereby adopted for calculating quasi-periodic QSOs that extend beyond the equatorial plane of Phobos. We refer to this type of orbits as “3D QSOs” and discuss an example of them in Sect. 2.4.

Despite the GMOS algorithm succeeds in generating three-dimensional QSOs, the numerical procedure remains cumbersome and computationally expensive. Accordingly, the purpose of this paper is to study the long-term evolution of 3D QSOs via GVE and the averaging process so as to

• gain analytical insight into the dynamical environment of planetary moons;

• provide high-quality initial guesses for trajectory optimization without GMOS;

• support onboard spacecraft operations with averaged analytical solutions to the relative motion problem.

2.2 General solution of the Keplerian relative motion problem

The EHP admits two equilibrium points in correspondence of $\tilde{\varvec{r}}^* = \begin{bmatrix} \pm (1/3)^{(1/3)}&0&0\end{bmatrix}^T$. These points of equilibrium are often referred to as Lagrangian points and delimit a region of the phase space where the dynamics is dominated by the gravity field of the secondary body. Since the magnitude of the gravitational force due to the secondary is proportional to the inverse squared distance between its barycenter and the spacecraft, the dynamics inside the red curves of Fig. 1 remains dominated by the primary body as long as $r^* = \epsilon \,p\,\gamma ^{-1}\,\tilde{r}^*$ is significantly smaller than $0.05\,a$. As a preliminary rule of thumb, let us consider the cases where

$$\begin{aligned}&r^* = \epsilon \,p\,\gamma ^{-1}\,\left( \dfrac{1}{3}\right) ^{1/3} \le \epsilon \,a\,(1+e)\,\left( \dfrac{1}{3}\right) ^{1/3}\nonumber \\&\quad < 0.005\,a, \end{aligned}$$

(6)

so that motion above $0.01\,a$ would be only slightly perturbed by the gravity field of the moon. This implies $\left( \dfrac{m}{3\,M}\right) ^{1/3}< \dfrac{0.005}{1 + e} < 0.005$ or $(m/M) < 3.75\times 10^{-7}$ like in the Mars–Phobos, Saturn–Enceladus, Sun–Mars, and many other three-body problems of the solar system.

In what follows, we consider the Mars–Phobos case as an example of a large class of three-body systems that comply with the assumptions of the elliptical Hill problem while satisfying the negligible mass conditions given by Eq. (6). Our goal is to describe the long-term evolution of mid-altitude quasi-satellite orbits crossing the positive x-axis between $0.01\,a$ and $0.025\,a$. We note that this corresponds to 93.77 km and 234.425 km for the Mars–Phobos system, which is the orbital region under consideration for the proximity operations of the Martian Moons eXploration mission [7].

Assuming that the gravitational attraction of Phobos is negligible, the dynamics of a satellite near the planetary satellite would be governed by the simplified set of equations given by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = u,\\ \dot{y} = v,\\ \dot{z} = w,\\ \dot{u} = 3\,\dfrac{x}{\gamma }\, + 2\,v,\\ \dot{v} = - 2\,u,\\ \dot{w} = -z. \end{array} \right. \end{aligned}$$

(7)

System (7) is equivalent to the Tschauner–Hempel equations describing the relative motion of two neighboring satellites in eccentric Keplerian orbits and was analytically solved by Yamanaka and Ankersen [24, 33]. The authors provide an expression for the relative position and velocity vectors in terms of the six integrals of motion $K_1$, $K_2$, $K_3$, $K_4$, $K_5$, $K_6$. The solution reads as

$$\begin{aligned} \left\{ \begin{array}{l} x(\nu ) = K_2\,\gamma \,\sin {\nu } + K_3\,\gamma \,\cos {\nu } \\ \quad + K_4\,(2 - 3\,e\,J\,\gamma \,\sin {\nu }),\\ y(\nu ) = K_1 + K_2\,(1 + \gamma )\,\cos {\nu } \\ \quad - K_3\,(1 + \gamma )\,\sin {\nu } - 3\,K_4\,J\,\gamma ^2,\\ z(\nu ) = K_5\,\sin {\nu } + K_6\,\cos {\nu },\\ u(\nu ) = K_2\,s^* + K_3\,c^* - 3\,e\,K_4\,\left( \dfrac{\sin {\nu }}{\gamma } + J\,s^*\right) ,\\ v(\nu ) = - 2\,K_2\,\gamma \,\sin {\nu } - K_3\,(2\,\gamma \,\cos {\nu } - e) \\ \quad - 3\,K_4\,(1 - 2\,e\,J\,\gamma \,\sin {\nu }),\\ w(\nu ) = K_5\,\cos {\nu } - K_6\,\sin {\nu }, \end{array}\right. \end{aligned}$$

(8)

where $s^* = \cos {\nu } + e\,\cos {2\,\nu }$, $c^* = -(\sin {\nu } + e\,\sin {2\,\nu })$, and J is an integral term defined as $J = \int _{\nu _0}^\nu \,1/\gamma (\tau )^2\,\text {d}\,\tau$.

Equation (8) can be easily rewritten in matrix form as $\varvec{X}(\nu ) = \varPhi (\varvec{r},\varvec{v},\nu )\,\varvec{K}$, with $\varvec{K} = \begin{bmatrix} K_1,&K_2,&K_3,&K_4,&K_5,&K_6\end{bmatrix}^T$. We note that the determinant of $\varPhi (\varvec{r},\varvec{v},\nu )$ is equal to $(e^2 - 1)$, so that the matrix is nonsingular for any $e \in [0, 1)$. It follows that the values of $\varvec{K}$ can be inferred from rectangular coordinates through the inverse transformation [34]

$$\begin{aligned} \varvec{K} = \varPhi (\varvec{r}\,\varvec{v},\nu )^{-1}\,\varvec{X}(\nu ). \end{aligned}$$

(9)

Following Cabral [23], auxiliary variables can be now introduced to gain geometrical insight into the analytical solution of the Tschauner–Hempel equations. Specifically, let

$$\begin{aligned} A_x&= K_3,\end{aligned}$$

(10a)

$$\begin{aligned} A_y&= K_2 - 3\,e\,J\,K_4, \end{aligned}$$

(10b)

$$\begin{aligned} \delta _x&= 2\,K_4,\end{aligned}$$

(10c)

$$\begin{aligned} \delta _y&= K_1 - 3\,J\,K_4,\end{aligned}$$

(10d)

$$\begin{aligned} A&= \sqrt{A_x^2 + A_y^2},\end{aligned}$$

(10e)

$$\begin{aligned} \alpha&= \arctan {\left( \dfrac{-A_y}{A_x}\right) },\end{aligned}$$

(10f)

$$\begin{aligned} B&= \sqrt{K_5^2 + K_6^2},\end{aligned}$$

(10g)

$$\begin{aligned} \beta&= \arctan {\left( \dfrac{K_6}{K_5}\right) } \end{aligned}$$

(10h)

so that

$$\begin{aligned} \left\{ \begin{array}{l} x(\nu ) = \gamma \,A\,\cos {(\nu + \alpha )} + \delta _x,\\ y(\nu ) = -(1 + \gamma )\,A\,\sin {(\nu + \alpha )} + \delta _y,\\ z(\nu ) = B\,\sin {(\nu + \beta )}.\\ \end{array}\right. \end{aligned}$$

(11)

Equation (11) reveals that a mass particle in orbit around a massless Phobos would remain in the vicinity of the Martian moon if A, $\delta _x$, and $\delta _y$ have no secular growth. This is guaranteed when $K_4 = 0$ as $A_y$ and $\delta _y$ would both remain constant regardless of the integral term appearing in Eqs. (10b) and (10d). If $K_4 = 0$, the trajectory described by the spacecraft in the equatorial plane becomes a pulsating ellipse with frequency $\omega _{xy} = 1$ and semimajor and semiminor axes equal to $(1 + \gamma )\,A$ and $\gamma \,A$, respectively. The phase angles $\alpha$ and $\beta$ represent the longitude and latitude of the satellite at periarion, i.e., when $\nu = 0$, as specified in Fig. 4. Meanwhile, the out-of-plane motion is decoupled from the planar one and follows an harmonic oscillation with amplitude B and frequency $\omega _z = 1$.

Fig. 4

Orbital evolution of a satellite in a 100-km quasi-QSO orbit with $\delta _x = \delta _y = 0$. The red point illustrates the position of the spacecraft at periarion, i.e., when $\nu = 0$

2.3 Gauss variational equations

As specified in Eq. (9), values of $\varvec{K}$ can be inferred from the Cartesian coordinates of a spacecraft while knowing the true anomaly of Phobos around Mars. In consequence, the total differential of $\varvec{K} = \varvec{K}(\varvec{r},\varvec{v},\nu )$ reads as

$$\begin{aligned} \dot{\varvec{K}} = \dfrac{\partial \varvec{K}}{\partial \varvec{r}}\,\dot{\varvec{r}} + \dfrac{\partial \varvec{K}}{\partial \varvec{v}}\,\dot{\varvec{v}} + \dfrac{\partial \varvec{K}}{\partial \nu }\, \end{aligned}$$

(12)

and must be equal to zero when the dynamics is governed by the unperturbed system (7), where $\dot{\varvec{v}} = \varvec{a} = \begin{bmatrix} 3\,\dfrac{x}{\gamma }\, + 2\,v,&-2\,u,&-z\end{bmatrix}^T$.

Let us now consider the perturbed dynamics

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\varvec{r}} = \varvec{v},\\ \dot{\varvec{v}} = \varvec{a} + \varvec{u}, \end{array} \right. \end{aligned}$$

(13)

where $\varvec{u} = \begin{bmatrix} u_x,&u_y,&u_z\end{bmatrix}^T$ is a vector of disturbing forces per unit mass in the pulsating synodic reference frame $S'$. Substituting Eq. (13) in Eq. (12) yields the GVE for the $\varvec{K}$ integrals of motion given by $\dot{\varvec{K}} = \dfrac{\partial \varvec{K}}{\partial \varvec{v}}\,\varvec{u}$ [34].

The rates of change for orbit elements A, $\alpha$, $\delta _x$, $\delta _y$, B, and $\beta$ can be deduced from the application of the chain rule and yield

$$\begin{aligned} \dot{A}&= - \left[ \dfrac{\gamma \,\sin {(\nu +\alpha )} - 2\,e\,\sin {\alpha }}{1 - e^2}\right] \,u_x \nonumber \\&\quad - \left[ \dfrac{e\,\cos {\alpha } + (1+\gamma )\,\cos {(\nu + \alpha )}}{1 - e^2}\right] \,u_y \nonumber \\&\quad + \dfrac{3\,e\,\sin {\alpha }}{2\,\gamma ^2}\,\delta _x, \end{aligned}$$

(14a)

$$\begin{aligned} \dot{\alpha }&= -\left[ \dfrac{\gamma \,\cos {(\nu +\alpha )} - 2\,e\,\cos {\alpha }}{A\,(1 - e^2)}\right] \,u_x \nonumber \\&\quad + \left[ \dfrac{e\,\sin {\alpha } + (1+\gamma )\,\sin {(\nu + \alpha )}}{A\,(1 - e^2)}\right] \,u_y\nonumber \\&\quad + \dfrac{3\,e\,\cos {\alpha }}{2\,A\,\gamma ^2}\,\delta _x,\end{aligned}$$

(14b)

$$\begin{aligned} \dot{\delta }_x&= \left( \dfrac{2\,e\,\gamma \,\sin {\nu }}{1-e^2}\right) \,u_x + \left( \dfrac{2\,\gamma ^2}{1-e^2}\right) \,u_y,\end{aligned}$$

(14c)

$$\begin{aligned} \dot{\delta }_y&= \left[ \dfrac{e\,\gamma \,\cos {\nu } - 2}{1 - e^2}\right] \,u_x - \left[ \dfrac{e\,(1+\gamma )\,\sin {\nu }}{1 - e^2}\right] \,u_y \nonumber \\&\quad - \dfrac{3}{2\,\gamma ^2}\,\delta _x,\end{aligned}$$

(14d)

$$\begin{aligned} \dot{B}&= \cos {(\nu + \beta )}\,u_z,\end{aligned}$$

(14e)

$$\begin{aligned} \dot{\beta }&= -\dfrac{\sin {(\nu + \beta )}}{B}\,u_z. \end{aligned}$$

(14f)

We note that the rate of change of the latitude at periarion is inversely proportional to the magnitude of the out-of-plane motion B. To avoid singularities, we consider

$$\begin{aligned} \dot{K_5}&= (\cos {\nu })\,u_z,\end{aligned}$$

(15a)

$$\begin{aligned} \dot{K_6}&= -(\sin {\nu })\,u_z. \end{aligned}$$

(15b)

instead of Eqs. (14e) and (14f) when studying the dynamical evolution of planar QSO orbits such as the one in Fig. 4. The final set of equations of motion for the osculating orbit elements becomes

(16)

where $\mathcal {M}$ is the phase space of the orbit elements ,

(17)

and is a six-by-three matrix with nonzero components

$$\begin{aligned} G_{1,1}&= -\dfrac{\gamma \,\sin {(\nu +\alpha )} - 2\,e\,\sin {\alpha }}{1 - e^2},\end{aligned}$$

(18a)

$$\begin{aligned} G_{1,2}&= -\dfrac{e\,\cos {\alpha } + (1+\gamma )\,\cos {(\nu + \alpha )}}{1 - e^2},\end{aligned}$$

(18b)

$$\begin{aligned} G_{2,1}&= -\dfrac{\gamma \,\cos {(\nu +\alpha )} - 2\,e\,\cos {\alpha }}{A\,(1 - e^2)},\end{aligned}$$

(18c)

$$\begin{aligned} G_{2,2}&= \dfrac{e\,\sin {\alpha } + (1+\gamma )\,\sin {(\nu + \alpha )}}{A\,(1 - e^2)},\end{aligned}$$

(18d)

$$\begin{aligned} G_{3,1}&= \dfrac{2\,e\,\gamma \,\sin {\nu }}{1-e^2},\end{aligned}$$

(18e)

$$\begin{aligned} G_{3,2}&= \dfrac{2\,\gamma ^2}{1-e^2},\end{aligned}$$

(18f)

$$\begin{aligned} G_{4,1}&= \dfrac{e\,\gamma \,\cos {\nu } - 2}{1 - e^2},\end{aligned}$$

(18g)

$$\begin{aligned} G_{4,2}&= -\dfrac{e\,(1+\gamma )\,\sin {\nu }}{1 - e^2},\end{aligned}$$

(18h)

$$\begin{aligned} G_{5,3}&= \cos {\nu },\end{aligned}$$

(18i)

$$\begin{aligned} G_{6,3}&= -\sin {\nu }. \end{aligned}$$

(18j)

Equation (16) can be now integrated to obtain the evolution of the osculating orbit elements without converting from the Cartesian coordinates adopted in Eq. (13). The system of ordinary differential equations will be referred to as GVE and validated against the numerical integration of the EHP in the next section. Furthermore, analytical expressions for the effects of Phobos’ gravity can be now derived and analyzed. The result of these investigations will produce a linear model that will be averaged and solved analytically in Section 6 to grasp the secular evolution of the QSO mean relative orbit elements.

2.4 The effects of Phobos’ gravity

Let us replace the terms $u_x$, $u_y$, $u_z$ appearing in (16) with the gravitational attraction of a spherical object with mass m significantly smaller than the mass of the primary ($M>> m$) in the pulsating reference frame $\mathcal {S}'$:

$$\begin{aligned} \varvec{u} = -\dfrac{1}{\gamma }\,\begin{bmatrix} x/r^3\\ y/r^3\\ z/r^3\end{bmatrix}, \end{aligned}$$

(19)

where $r(\nu ) = \sqrt{x(\nu )^2 + y(\nu )^2 + z(\nu )^2}$. Based on Eq. (11), r changes as a function of the relative orbit elements through a fairly complicated expression that yields the instantaneous relative distance between the satellite and the barycenter of the secondary body, e.g., Phobos. Nevertheless, a satellite on a QSO orbit remains close to the equatorial plane of the Martian moon if $\delta _x$ and $\delta _y$ are close to zero. In addition, the eccentricity of the Phobos is relatively small and allows for simplifications in the expressions of the GVE presented in Sect. 3. These considerations justify the first-order expansion of the equations of motion in e, $\delta = \left( \dfrac{\delta _x}{A}\right)$, $\chi = \left( \dfrac{\delta _y}{A}\right)$, $\eta _5 = \left( \dfrac{K_5}{A}\right)$, $\eta _6 = \left( \dfrac{K_6}{A}\right)$ under the assumption that $\delta , \chi , \eta _5, \eta _6 ~ \mathcal {O}(e)<< 1$. This assumption was investigated by Cabral in [23] and seems to be reliable for mid-altitude QSO orbits based on numerical experiments. In this orbital regime, the expressions of x, y, and z in Eq. (11) imply

$$\begin{aligned}&r(\varvec{e}) \simeq A\,\left\{ d^2 + 2\,e\,\cos {\nu }\,\left[ \cos ^2{\theta } + 2\,\sin ^2{\theta }\right] \right. \nonumber \\&\left. \quad +\, 2\,\delta \,\cos {\theta } - 4\, \chi \,\sin {\theta }\right\} ^{1/2}, \end{aligned}$$

(20)

where $\varvec{e} = \begin{bmatrix} e,&\delta ,&\chi \end{bmatrix}^T$, $d = \sqrt{\cos ^2{\theta } + 4\,\sin ^2{\theta }}$, and $\theta = \nu + \alpha$.

Replacing the $u_x$, $u_y$, and $u_z$ terms of Eq. (14c) with (19) then yields

$$\begin{aligned}&\dot{\delta }_x \simeq \dfrac{2\,A}{[r(\varvec{e})]^3}\,\left\{ 2\,\sin {\theta } + e\,\left[ 3\,\cos {\nu }\,\sin {\theta } - \sin {\nu }\,\cos {\theta }\right] - \chi \right\} ,\nonumber \\&\quad \simeq \dfrac{2}{A^2}\,\left\{ \left[ \dfrac{2\,\sin {\theta } + e\,\left[ 3\,\cos {\nu }\,\sin {\theta } - \sin {\nu }\,\cos {\theta }\right] - \chi }{d^3}\right] \right. \nonumber \\&\quad \left. -6\,\sin {\theta }\,\left[ \dfrac{e\,\cos {\nu }\,\left[ \cos ^2{\theta } {+} 2\,\sin ^2{\theta }\right] {+} \delta \,\cos {\theta } {-} 2\,\chi \,\sin {\theta }}{d^5}\right] \right\} . \end{aligned}$$

(21)

Similarly, the other GVEs become

$$\begin{aligned} \dot{A}&\simeq \dfrac{1}{A^2\,d^3}\,\left\{ -\dfrac{3}{2}\,\sin {(2\,\theta )} - 2\,e\,\left[ \sin {(\nu + 2\,\alpha )} - 0.25\,\cos {\nu }\,\sin {(2\,\theta )}\right] + \delta \,\sin {\theta } + 2\,\chi \,\cos {\theta }\right. \nonumber \\&\quad \left. +\dfrac{9}{2}\,\sin {(2\,\theta )}\,\left[ \dfrac{e\,\cos {\nu }\,\left( \cos ^2{\theta } + 2\,\sin ^2{\theta }\right) + \delta \,\cos {\theta } - 2\,\chi \,\sin {\theta }}{d^2}\right] \right\} , \end{aligned}$$

(22a)

$$\begin{aligned} \dot{\alpha }&\simeq \dfrac{1}{A^3}\,\left\{ \dfrac{1}{d} - e\,\dfrac{\cos {\nu }}{d}- \dfrac{e\,\left[ 2\,\cos {(\nu + 2\,\alpha )} + \cos {\nu }\,(\cos ^2{\theta } + 2\,\sin ^2{\theta })\right] + 2\,\delta \,\cos {\theta } - 4\,\chi \,\sin {\theta }}{d^3}\right\} , \end{aligned}$$

(22b)

$$\begin{aligned} \dot{\delta }_y&\simeq \dfrac{1}{A^2\,d^3}\,\left\{ 2\,\cos {\theta } - e\,\left[ \cos {\nu }\,\cos {\theta } + 4\,\sin {\nu }\,\sin {\theta }\right] \right. \nonumber \\&\left. \quad + \delta \,\left( \dfrac{4 - 3\,A^3\,d^3}{2}\right) -6\,\cos {\theta }\,\left[ \dfrac{e\,\cos {\nu }\,\left( \cos ^2{\theta } + 2\,\sin ^2{\theta }\right) + \delta \,\cos {\theta } - 2\,\chi \,\sin {\theta }}{d^2}\right] \right\} , \end{aligned}$$

(22c)

$$\begin{aligned} \dot{K}_5&\simeq -\dfrac{\cos {\nu }}{A^2}\,\left( \dfrac{\eta _5\,\sin {\nu } + \eta _6\,\cos {\nu }}{d^3}\right) , \end{aligned}$$

(22d)

$$\begin{aligned} \dot{K}_6&\simeq \dfrac{\sin {\nu }}{A^2}\,\left( \dfrac{\eta _5\,\sin {\nu } + \eta _6\,\cos {\nu }}{d^3}\right) , \end{aligned}$$

(22e)

or

(23)

in vectorial form.

Equation (23) summarizes a linear model (LM) in e, $\delta$, $\chi$, $\eta _5$, and $\eta _6$ that accurately predicts the dynamics of mass particles in mid- and high-altitude QSO orbits for several orbital periods around Phobos. This claim is supported by Figs. 5 6 7 and 8, which compare trajectories of the original and linearized systems obtained by numerical integration of the same set of initial conditions:

(24)

in Cartesian coordinates and osculating orbit elements, respectively, with $\nu _0 = 324.8780$ deg. Table 1 summarizes the models and relevant assumptions introduced throughout these subsections.

Table 1 Dynamical models and corresponding assumptions

As depicted in Fig. 8a, the error between the integration of Eqs. (16) and (13) is purely numerical and negligible after 100 orbital revolutions of Phobos around Mars (i.e., almost 32 days). In contrast, the position error of the linearized model exhibits a secular growth, but never exceeds 5 kilometers over the same interval of time. Such an error is deemed reasonable for the purpose of this article, as navigation errors and mismodeled dynamics would likely overtake the inaccuracies of the linearized model over the time span of a few days. Accordingly, the LM is considered as a good candidate for describing the long-term evolution of satellites in mid-altitude QSO orbits and can be used for the analysis of the secular motion as described in the following section.

Fig. 5

Quasi-QSO orbit integrated over 100 Phobos revolution with the LM (blue) and GVEs (red) models

Fig. 6

Variables A, $\alpha$, $\delta _x$, $\delta _y$ obtained with the LM (blue) and GVEs (red) models

Fig. 7

Variables $K_5$, $K_6$, B, $\beta$ obtained with the LM (blue) and GVEs (red) models

Fig. 8

a Position error between the GVEs and EHP models. b Position error between the LM and EHP models

3 Averaged equations

The long-term evolution of quasi-QSO orbits is now analyzed by averaging Eq. (23) over one orbital period around Phobos, i.e., . We find that the averaged orbit elements $\bar{A}$, $\bar{\alpha }$, $\bar{\delta }_x$, $\bar{\delta }_y$, $\bar{K}_5$, and $\bar{K}_6$ evolve with the true anomaly as

$$\begin{aligned} \dot{\bar{A}}&= 0, \end{aligned}$$

(25a)

$$\begin{aligned} \dot{\bar{\alpha }}&= \dfrac{\mathcal {K}}{\pi \,\bar{A}^3}, \end{aligned}$$

(25b)

$$\begin{aligned} \dot{\bar{\delta }}_x&= -2\,\dfrac{e}{\bar{A}^2}\,\left( \dfrac{\mathcal {K} - 7\,\mathcal {E}}{9\,\pi }\right) \,\sin {\bar{\alpha }} + 2\,\dfrac{\bar{\delta }_y}{\bar{A}^3}\,\left( \dfrac{\mathcal {K} - \mathcal {E}}{3\,\pi }\right) ,\end{aligned}$$

(25c)

$$\begin{aligned} \dot{\bar{\delta }}_y&= \dfrac{e}{\bar{A}^2}\,\left( \dfrac{\mathcal {K} - 52\,\mathcal {E}}{9\,\pi }\right) \,\cos {\bar{\alpha }} -\dfrac{3}{2}\,\bar{\delta }_x \nonumber \\&\quad + 2\,\dfrac{\bar{\delta }_x}{\bar{A}^3}\,\left( \dfrac{\mathcal {K} - 4\,\mathcal {E}}{3\,\pi }\right) ,\end{aligned}$$

(25d)

$$\begin{aligned} \dot{\bar{K}}_5&= -\dfrac{\bar{K}_5}{\bar{A}^3}\,\left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi }\right) \,\sin {(2\,\bar{\alpha })} - \dfrac{\bar{K}_6}{\bar{A}^3}\,\dfrac{\mathcal {E}}{2\,\pi } \nonumber \\&\quad + \dfrac{\bar{K}_6}{\bar{A}^3}\,\left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi }\right) \,\cos {(2\,\bar{\alpha })}, \end{aligned}$$

(25e)

$$\begin{aligned} \dot{\bar{K}}_6&= \dfrac{\bar{K}_5}{\bar{A}^3}\,\dfrac{\mathcal {E}}{2\,\pi } + \dfrac{\bar{K}_5}{\bar{A}^3}\,\left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi }\right) \,\cos {(2\,\bar{\alpha })}\nonumber \\&\quad + \dfrac{\bar{K}_6}{\bar{A}^3}\,\left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi }\right) \,\sin {(2\,\bar{\alpha })}, \end{aligned}$$

(25f)

where $\mathcal {K} \simeq 2.156516$ and $\mathcal {E} \simeq 1.211056$ are the complete elliptical integrals of the first and second kind, respectively, evaluated with modulus $k = \sqrt{3}/2$ [35].

We note here that our expressions approach the ones of Kogan [20] whenever $e \rightarrow 0$, but differ from the ones found in Cabral’s thesis [23]. There, the author derived secular equations using Lagrange planetary equations on the averaged disturbing potential due to the gravity field of Phobos, omitting the $-\dfrac{3}{2}\,\bar{\delta }_x$ term appearing in Eq. (25d). Coefficients that model the long-term evolution of the relative orbit elements are also presented differently and in terms of different elliptical integrals, leading to erroneous frequencies of motion.

Equation (25) exhibits cross-coupling between some of the orbit elements, as well as long-term oscillations due to the secular growth of $\alpha$, i.e., the longitude at periarion. Such a growth causes the geometry between the spacecraft, Mars, and Phobos, to change at every periarion passage, i.e., when the gravitational attraction of Mars is at its strongest. To grasp the secular effects of this phenomenon, observe that $\bar{\alpha }$ grows linearly with the true anomaly and with a rate $\omega _\alpha = (\mathcal {K}/\pi )\,\bar{A}^{-3} \simeq 0.686440\,\bar{A}^{-3}$ that depends on the amplitude of the in-plane motion:

$$\begin{aligned} \bar{\alpha }(\nu ) = \omega _\alpha \,(\nu - \nu _0) + \bar{\alpha }_0, \end{aligned}$$

(26)

where $\bar{\alpha }_0 = \bar{\alpha }(\nu _0)$, and $\nu _0$ is the true anomaly of Phobos at epoch.

Observe that $\omega _\alpha$ is constant due to Eq. (25a). Furthermore, the value of $\omega _\alpha$ defines the period of the QSO orbit via $T = 2\,\pi /n_{QSO}$ and $n_{QSO} = \dot{\theta } = \dot{\nu } + \dot{\alpha } \simeq 1 + \omega _\alpha$. This relationship is demonstrated with the chart of Fig. 9, illustrating the comparison between the analytical prediction of $n_{QSO}$ and the numerical value computed with the GMOS algorithm of Sect. 2.1. We find that the proposed linearization and averaging approach are valid as long as $\bar{A} > 3.36$, corresponding to 80 km for the Mars–Phobos system.

Fig. 9

Comparison between the numerical value of $n_{QSO}$ and its theoretical prediction $1 + \dot{\bar{\alpha }}$. The time unit TU is equal to 1.288 h

In the validity regime of Eq. (25), the in-plane and out-of-plane components of motion can be decoupled and reduced to the linear systems

$$\begin{aligned} \begin{bmatrix} \dot{\bar{\delta }}_x\\ \dot{\bar{\delta }}_y\end{bmatrix}= & {} \begin{bmatrix} 0 &{} D_x\\ D_y &{} 0\end{bmatrix}\,\begin{bmatrix}\bar{\delta }_x\\ \bar{\delta }_y \end{bmatrix} - e\,\begin{bmatrix} d_x\,\sin {\bar{\alpha }}\\ d_y\,\cos {\bar{\alpha }}\end{bmatrix}, \end{aligned}$$

(27)

$$\begin{aligned} \begin{bmatrix} \dot{\bar{K}}_5\\ \dot{\bar{K}}_6\end{bmatrix}= & {} \begin{bmatrix} -\zeta \,\sin {(2\,\bar{\alpha })} &{} -\varUpsilon + \zeta \,\cos {(2\,\bar{\alpha })}\\ \varUpsilon + \zeta \,\cos {(2\,\bar{\alpha })} &{} \zeta \,\sin {(2\,\bar{\alpha })}\end{bmatrix}\, \begin{bmatrix} \bar{K}_5\\ \bar{K}_6\end{bmatrix},\nonumber \\ \end{aligned}$$

(28)

where

$$\begin{aligned} D_x&= 2\,\left( \dfrac{\mathcal {K} - \mathcal {E}}{3\,\pi \,\bar{A}^3}\right) > 0,\end{aligned}$$

(29a)

$$\begin{aligned} D_y&= -\dfrac{3}{2} + 2\,\left( \dfrac{\mathcal {K} - 4\,\mathcal {E}}{3\,\pi \,\bar{A}^3}\right) < 0,\end{aligned}$$

(29b)

$$\begin{aligned} d_x&= 2\,\left( \dfrac{\mathcal {K} - 7\,\mathcal {E}}{9\,\pi \,\bar{A}^2}\right) < 0,\end{aligned}$$

(29c)

$$\begin{aligned} d_y&= \left( \dfrac{52\,\mathcal {E} - \mathcal {K}}{9\,\pi \,\bar{A}^2}\right) > 0, \end{aligned}$$

(29d)

and

$$\begin{aligned} \zeta&= \left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi \,\bar{A}^3}\right) ,\end{aligned}$$

(30a)

$$\begin{aligned} \varUpsilon&= \dfrac{\mathcal {E}}{2\,\pi \,\bar{A}^3}. \end{aligned}$$

(30b)

Fig. 10

Maximum $\bar{\delta }_x$ deviations as a function of the initial conditions $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$ when $e = 0$

Using the Laplace transform, we find that the secular evolution of $\bar{\delta }_x$ and $\bar{\delta }_y$ becomes

$$\begin{aligned} \bar{\delta }_x(\nu )&= \left[ \bar{\delta }_{x,0} - e\,d_1\,\cos {(\bar{\alpha }_0)}\right] \,\cos {(\omega _d\,\tilde{\nu })} \ldots \nonumber \\&\,\quad + \left[ \bar{\delta }_{y,0}\,\left( \dfrac{D_x}{\omega _d}\right) + e\,\left( \dfrac{\omega _d}{D_y}\right) \,d_2\,\sin {(\bar{\alpha }_0)}\right] \nonumber \\&\qquad \sin {(\omega _d\,\tilde{\nu })} + e\,d_1\,\cos {(\bar{\alpha })},\end{aligned}$$

(31a)

$$\begin{aligned} \bar{\delta }_y(\nu )&= \left[ \bar{\delta }_{x,0}\,\left( \dfrac{D_y}{\omega _d}\right) + e\,\left( \dfrac{\omega _d}{D_x}\right) \,d_1\,\cos {(\bar{\alpha }_0)}\right] \nonumber \\&\qquad \sin {(\omega _d\,\tilde{\nu })} \ldots \nonumber \\&\,\quad + \left[ \bar{\delta }_{y,0} - e\,d_2\,\sin {(\bar{\alpha }_0)}\right] \,\cos {(\omega _d\,\tilde{\nu })}\nonumber \\&\quad + e\,d_2\,\sin {(\bar{\alpha })}, \end{aligned}$$

(31b)

where $\tilde{\nu } = (\nu - \nu _0)$, $\bar{\delta }_{x,0} = \bar{\delta }_x(\nu _0)$, $\bar{\delta }_{y,0} = \bar{\delta }_{y}(\nu _0)$,

$$\begin{aligned} d_1&= \left( \dfrac{D_x\,d_y + \omega _\alpha \,d_x}{\omega _\alpha ^2 - \omega _d^2}\right) ,\end{aligned}$$

(32a)

$$\begin{aligned} d_2&= \left( \dfrac{D_y\,d_x - \omega _\alpha \,d_y}{\omega _\alpha ^2 - \omega _d^2}\right) , \end{aligned}$$

(32b)

and

$$\begin{aligned} \omega _d^2= & {} -D_x\,D_y = \dfrac{\mathcal {K} - \mathcal {E}}{\pi \,\bar{A}^3} - \dfrac{4}{9}\,\left( \dfrac{\mathcal {K}^2 - 5\,\mathcal {K}\,\mathcal {E} + 4\,\mathcal {E}^2}{\pi ^2\,\bar{A}^6}\right) \nonumber \\\simeq & {} 0.30095\,\bar{A}^{-3} - 0.11443\,\bar{A}^{-6}. \end{aligned}$$

(33)

The motion of the center of the in-plane ellipse is therefore characterized by two frequencies whose ratio is given by $\omega _\alpha /\omega _d \simeq 1.251283\,\bar{A}^{-1.5}$. In the limiting case $e \rightarrow 0$, such a center traces out ellipses in the $(\bar{\delta }_x, \bar{\delta }_y)$ plane with period $2\,\pi /\omega _d$. The maximum deviations in $\bar{\delta }_x$ and $\bar{\delta }_y$ occur at $(\omega _d\,\tilde{\nu })_{\bar{\delta }_x} = \arctan {\left( \dfrac{D_x\,\bar{\delta }_{y,0}}{\omega _d\,\bar{\delta }_{x,0}}\right) }$ and $(\omega _d\,\tilde{\nu })_{\bar{\delta }_y} = \arctan {\left( \dfrac{D_y\,\bar{\delta }_{x,0}}{\omega _d\,\bar{\delta }_{y,0}}\right) }$, respectively, and can be quantified numerically for different values of $\bar{A}$ as in Figs. 10 and 11. In the plots of Figs. 10 and 11, we ignore those combinations of $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$, and $\bar{A}$ for which the maximum values of $\bar{\delta }_x$, $\bar{\delta }_y$ violate the linearization assumptions of Sect. 5, i.e., $\delta \simeq \dfrac{\bar{\delta }_x}{\bar{A}} < 0.1$, $\chi \simeq \dfrac{\bar{\delta }_y}{\bar{A}} < 0.1$. As a result, we obtain a preliminary visualization of the $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$ values that comply with the validity requirements of Eq. (31).

Fig. 11

Maximum $\bar{\delta }_y$ deviations as a function of the initial conditions $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$ when $e = 0$

Within this region, the eccentricity of the secondary body plays an important role by introducing $\bar{\delta }_x$ and $\bar{\delta }_y$ oscillations regardless of the initial conditions $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$, $\bar{\alpha }_0$. To quantify these effects, we investigate the magnitudes of the terms proportional to the eccentricity in Eq. (31) over a uniform grid of $\bar{A} \in [3.36\,,\,7]$ values (corresponding to approximately 80 and 160 km for the Mars–Phobos system). The results of this analysis are portrayed in Fig. 12 and reveal that $\bar{\delta }_y/\bar{A}$ oscillations can be as large as $4.45\,e$ even when $\bar{\delta }_{x,0} = \bar{\delta }_{y,0} = 0$. In the worst-case scenario, $\bar{\alpha }_0 = \pm \pi /2$, the validity of Eq. (31) holds as long as the eccentricity of the secondary is no larger than 0.022. In contrast, when $\bar{\alpha }_0 = 0$ or $\pi$, librations of $\bar{\delta }_y/\bar{A}$ do not violate the linearization assumptions of Sect. 5 for eccentricities up to 0.044.

Fig. 12

Relative magnitude of the terms proportional to the eccentricity of the secondary body as a function of $\bar{A}$. The top panel refers to terms in $\bar{\delta }_x$, whereas the bottom panel is for terms in $\bar{\delta }_y$

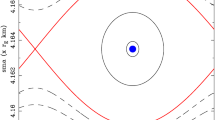
Assuming the validity of Eq. (31) with $\bar{\delta }_{x,0} = \bar{\delta }_{y,0} = 0$, the eccentricity of the secondary body causes quasi-periodic oscillations in $\bar{\delta }_x$ and $\bar{\delta }_y$ that densely cover the surface of a two-dimensional invariant torus with frequencies $\omega _\alpha < \omega _d$. The general case (e, $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0} \ne 0$) is a linear combination of the two limiting scenarios in which the center of the in-plane relative trajectories remains bounded with respect to the origin of the coordinate system. An interesting situation occurs for those values of $\bar{A}$ for which $\omega _d / \omega _\alpha$ is rational. In this resonant case, the motion of the center becomes fully periodic in the $\bar{\delta }_x$, $\bar{\delta }_y$ plane as illustrated in Fig. 13d.

Fig. 13

Examples of $\bar{\delta }_x$, $\bar{\delta }_y$ motion for different combinations of e, $\bar{\delta }_{x,0}$, $\bar{\delta }_{y,0}$ and $\bar{A}$ values. All of the trajectories have been computed assuming $\bar{\alpha }_0 = 0$ rad. Note the different scales of the axes as well as that the value of $\bar{A}$ in the bottom right panel has been computed so that $\omega _d/\omega _\alpha = 5$

Concerning the out-of-plane component, we observe that neither of Eqs. (22d), (22e), (25e), and (25f) depend on the eccentricity of Phobos’ orbit. The same situation occurs when considering the expressions of $\dot{B}$ and $\dot{\beta }$ instead of Eqs. (22d) and (22e):

$$\begin{aligned} \dot{B}&\simeq -\dfrac{B}{2\,A^3\,d^3}\,\sin {[2\,(\theta - \varphi )]} \end{aligned}$$

(34a)

$$\begin{aligned} \dot{\beta }&\simeq \dfrac{\sin ^2{(\theta - \varphi )}}{A^3\,d^3}\,\bigg \{1 - 4\,e\,\cos {(\theta - \alpha )} \nonumber \\&\quad + \dfrac{6\,e\,\cos {(\theta {-} \alpha )}\sin ^2{(\theta )} {+} 6\,\delta \,\sin {\theta } {-} 3\,\chi \cos {\theta }}{d^2} \bigg \}, \end{aligned}$$

(34b)

where $\varphi = (\alpha - \beta )$ is the relative phase between the longitude and latitude at periarion.

By averaging over one orbital period, the differential equations of $\bar{B}$ and $\bar{\beta }$ read as

$$\begin{aligned} \dot{\bar{B}}&= -\left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi \,\bar{A}^3}\right) \,\bar{B}\,\sin {(2\,\bar{\varphi })} \end{aligned}$$

(35a)

and

$$\begin{aligned} \dot{\bar{\beta }}&= \dfrac{\mathcal {E}}{2\,\pi \,\bar{A}^3} + \left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi \,\bar{A}^3}\right) \,\cos {(2\,\bar{\varphi })}, \end{aligned}$$

(35b)

respectively. The true anomaly rate of change of $\bar{\varphi }$ becomes

$$\begin{aligned} \dot{\bar{\varphi }} = \left( \dfrac{2\,\mathcal {K} - \mathcal {E}}{2\,\pi \,\bar{A}^3}\right) - \left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\pi \,\bar{A}^3}\right) \,\cos {(2\,\bar{\varphi })} \end{aligned}$$

(36)

and admits

$$\begin{aligned} \bar{\varphi }(\nu ) = \arctan {\left\{ \dfrac{1}{2}\,\sqrt{\dfrac{2\,\mathcal {K} + \mathcal {E}}{\mathcal {K} - \mathcal {E}}}\,\tan {\left[ \omega _\varphi \,(\nu - \nu _0) + \phi \right] }\right\} } \end{aligned}$$

(37)

as an analytical solution with

$$\begin{aligned} \omega _\varphi= & {} 2\,\dfrac{\sqrt{2\,\mathcal {K}^2 - \mathcal {K}\,\mathcal {E} - \mathcal {E}^2}}{3\,\pi \,\bar{A}^3}\nonumber \\= & {} 0.70649\,\omega _\alpha \simeq 0.484965\,\bar{A}^{-3}, \end{aligned}$$

(38)

$\phi = \arctan {\left[ 2\,\sqrt{\dfrac{\mathcal {K} - \mathcal {E}}{2\,\mathcal {K} - \mathcal {E}}}\,\tan {\bar{\varphi }_0}\right] }$, and $\bar{\varphi }_0 = \bar{\varphi }(\nu _0)$. By plugging Eq. (37) in Eq. (35), we find

$$\begin{aligned} \bar{B}(\nu ) = \mathcal {B}_0\,\left[ 1 - B_\varphi \,\cos {(2\,\bar{\varphi })}\right] ^{-1/2}, \end{aligned}$$

(39)

where $B_\varphi = \left( \dfrac{2\,\mathcal {K} - 5\,\mathcal {E}}{6\,\mathcal {K} - 3\,\mathcal {E}}\right) \simeq -0.18722$, $\mathcal {B}_0 = \bar{B}_0\,\sqrt{1 - B_\varphi \,\cos {(2\,\bar{\varphi }_0)}}$, and $\bar{B}_0 = \bar{B}(\nu _0)$. This result illustrates that the amplitude of the out-of-plane motion oscillates with a frequency of $2\,\omega _\varphi \simeq 1.4\,\omega _\alpha$ and is bounded by $\bar{B}_{max} = \bar{B}_0\,\sqrt{\frac{1 - B_\varphi }{1 + B_\varphi }} \simeq 1.20859\,\bar{B}_0$. Accordingly, in order to satisfy the linearization assumptions of Sect. 5, $\bar{B}_0$ must be less than or equal to $0.08274\,\bar{A}$ (corresponding to approximately 8 km in the Mars–Phobos system when $\bar{A} = 4.18 \simeq 100$ km). Also notice that $\bar{\beta }$ varies with a time-varying frequency $\omega _\beta \in \begin{bmatrix} \dfrac{\mathcal {K} - \mathcal {E}}{3\,\pi \,\bar{A}^3}\,,\,\dfrac{4\,\mathcal {E} - \mathcal {K}}{3\,\pi \,\bar{A}^3}\end{bmatrix}$ that is always smaller than $\omega _\alpha$. Moreover, analytical expressions for the evolution of $\bar{K}_5$ and $\bar{K}_6$ can be finally derived:

$$\begin{aligned}&\bar{K}_5(\nu ) = \bar{B}(\nu )\,\cos {\bar{\beta }(\nu )} \nonumber \\&\quad = \mathcal {B}_0\,\left[ 1 - B_\varphi \,\cos {(2\,\bar{\varphi })}\right] ^{-1/2}\,\cos {(\bar{\alpha } - \bar{\varphi })}, \end{aligned}$$

(40a)

and

$$\begin{aligned}&\bar{K}_6(\nu ) = \bar{B}(\nu )\,\sin {\bar{\beta }(\nu )} \nonumber \\&\quad = \mathcal {B}_0\,\left[ 1 - B_\varphi \,\cos {(2\,\bar{\varphi })}\right] ^{-1/2}\,\sin {(\bar{\alpha } - \bar{\varphi })}, \end{aligned}$$

(40b)

respectively.

We note that both of Eqs. (31) and (40) depend on sines and cosines multiplied by time-periodic amplitudes at worst. This observation confirms that 3D quasi-QSO orbits are stable for as long as the assumptions of the LM model are valid. To validate this hypothesis, we apply the analytical solution of System (25) to obtain the dynamical evolution of a spacecraft under the assumption that . Figure 14 shows the behavior of the mean orbit elements $\bar{\delta }_x$ and $\bar{\delta }_y$ obtained from the osculating orbit elements of Eq. (24) over 400 orbital revolutions. Although the secular evolutions of $\bar{\delta }_x$ and $\bar{\delta }_y$ differ quite significantly from the osculating values, we find that the trajectory of the spacecraft does not drift away from the vicinity of Phobos’ orbit. This shows that, in the averaged system, trajectories are bounded even when $\bar{\delta }_x$ is not exactly zero. At the same time, we can also conclude that an appropriate transformation between osculating and mean orbit element is mandatory in order to adequately capture the secular evolution of spacecraft in mid-altitude QSOs. The problem of finding accurate initial conditions for the averaged system is addressed in the next section along with the numerical validation and analysis of Eqs. (31) and (40).

Fig. 14

Evolution of the in-plane center of motion over 400 Phobos revolutions with

4 Mean-to-osculating orbit element mapping

In order to provide a detailed mapping between mean and osculating orbit elements, different methods of perturbation theories can be considered (see for instance [22, 36] and references therein). We choose to introduce the near-identity transformation $T: [0, 2\,\pi ] \times \mathcal {M} \rightarrow \mathcal {M}$ so as to reconstruct the unbiased oscillations of motion of the original system from the averaged trajectories. That is,

(41)

where $\epsilon$ is a formal small parameter (consider $\epsilon \simeq A^{-2}$ for practical purposes) emphasizing the slow evolution of the mean orbit elements with respect to the fast variables $\nu$. Under this assumption, the averaged dynamics given by Eq. (25) may be rewritten in vectorial form as , whereas

(42)

in agreement with Eq. (23) and the formal definition . From the true anomaly rate of change of Eq. (41), it now follows that

(43a)

which implies

(44)

up to the first order in $\epsilon$. To obtain unbiased oscillations, let us also impose the integral constraint

(45)

so that the analytical solution of the problem (44)–(45) may be written as [37]:

(46)

Equation (46) is a Fourier series that depends on the Fourier coefficients $\varvec{g}_{\epsilon }^{(k)}$ of . The series is practically truncated at the N-th order in computer implementations, where N is an adequate high number.

We highlight that transforming $\delta _x$ first is mandatory for the problem at hand. On the one hand, the oscillations of $\bar{\delta }_x$ are $\epsilon$-small as long as the satellite remains on a mid-altitude 3D QSO orbit like the one in Fig. 5. This argument can be verified by inspection of the osculating and averaged evolution of $\delta _x$ portrayed in Fig. 6. On the other hand, the differential equation of $\dot{\bar{\delta }}_y$ contains a linear term in $\bar{\delta }_x$ that is not multiplied by $\epsilon$-small coefficients, i.e., $\dfrac{3}{2}\,\bar{\delta }_x$. Hence, an $\epsilon$-small error would be introduced in the $\epsilon$-slow dynamics of $\bar{\delta }_y$ if $\bar{\delta }_x$ is not properly handled (i.e., if oscillations of $\delta _x$ are biased with respect to $\bar{\delta }_x$ at epoch).

To improve the accuracy of the near-identity transformation, we propose the nested transformation

(47)

where $T_{\delta _x}$ and $T_{\delta _y}$ represent the $\delta _x$ and $\delta _y$ components of the T map. The advantages of the nested approach are illustrated in the plots of Fig. 15, portraying the reconstruction of $\delta _y$ from $\bar{\delta }_y$ with and without the preemptive transformation of $\delta _x$ (Fig. 15a, b, respectively). As it can be seen, the nested transformation performs much better than the classic one by accurately reconstructing the short-periodic oscillations of $\delta _y$ up to 25 Phobos revolutions around Mars (8 days circa). In contrast, the biased value of $\bar{\delta }_x(\nu _0)$ at the epoch of Fig. 15b causes larger oscillations in $\bar{\delta }_y$ that translate into inaccurate osculating values.

Fig. 15

a Osculating (black), mean (red) and reconstructed (dashed red) values of $\delta _y$ with preemptive transformation of $\delta _x$. b Osculating (black), mean (blue) and reconstructed (dashed blue) values of $\delta _y$ without the preemptive transformation of $\delta _x$

Based on this result, we apply the nested approach to calculate an approximate value of and compare the numerical integration of (25) with Eqs. (31) and (40). The averaged initial conditions obtained from Eq. (24) are

(48)

and yield the relative errors of Fig. 16. We find that the relative error is negligible and use this information to validate our analytical developments.

We can also investigate the long-term evolution of mid-altitude QSO orbits and compare it with the osculating orbit elements obtained in Section 2.4. Starting from the in-plane component of motion, it is found that satellites in orbit around Phobos trace out prolate ellipses whose center oscillates in the $\delta _y$ direction. This is verified in the plot of Fig. 17, illustrating the evolution of a typical QSO orbit in the $\delta _x$–$\delta _y$ plane along with the analytical solution presented in Eq. (31).

Fig. 16

Relative error between numerically integrated and analytical mean orbit elements

Fig. 17

In-plane offset evolution over 100 Phobos orbits

Fig. 18

Out-of-plane motion over 400 Phobos orbits

Similar comparisons can be carried out for the values of $K_5$ and $K_6$ by noting that the out-of-plane component of motion should follow a pulsating circle with radius $\bar{B}(\nu )$. This behavior is demonstrated in the chart of Fig. 18 after integrating the initial conditions of Fig. 5 for 400 orbital periods of Phobos (128 days circa). The numerical simulation provides us with the time histories of the $\alpha$, $\beta$, and $\varphi$ angles disclosed in Fig. 19, thus proving that the true anomaly rate of change of the $\alpha$ and $\varphi$ angles is also in good agreement with the analytical values derived in Eqs. (26) and (38), respectively.

Fig. 19

$\alpha$, $\beta$, and $\varphi$ angles evolution over 100 Phobos orbits

Finally, Fig. 20 shows the osculating and averaged values of the in-plane amplitude A, thereby demonstrating that the secular evolution of mid-altitude 3D QSOs can be adequately captured by Eq. (46).

Fig. 20

Mean (red) and osculating (black) values of A over 100 Phobos orbits

5 Conclusions

This paper investigated quasi-satellite orbits around small secondary bodies to gain analytical insight into the elliptical restricted three-body problem. Starting from gravitational perturbation of the Tschauner–Hempel equations, we considered small eccentricities, in-plane, and out-of-plane oscillations to simplify the expressions of the QSO relative orbit elements rates of change with respect to the true anomaly of the secondary body. The linearized model obtained through these developments depends on the relative longitude between the spacecraft and the secondary attractor, which is a fast variable comparing to QSO orbit amplitude, offsets, and phase angles at epoch. Based on this observation, the equations of motion were averaged over one orbital period and solved analytically. We found that the eccentricity of the secondary body plays a key role by triggering librations in the radial and along-track directions of the primaries co-rotating frame. It was also verified that the amplitude of the relative motion remains constant as long as the assumptions of the linearized model are valid. These results extend the stability of near-equatorial retrograde orbits to the elliptical Hill problem, thereby validating the selection of QSO orbits for the proximity operations of future spacecraft missions to eccentric planetary moons (e.g., the Phobos sample retrieval MMX mission).

Future work will explore the advantages offered by the analytical solution of the averaged relative motion problem to the mission design and operations around small eccentric bodies. Apart from providing better initial guesses for trajectory design in full-ephemeris model, our analytical derivations will be used for onboard spacecraft operations and orbit maintenance analyses of the MMX mission. Indeed, avoiding numerical integrations is crucial because of the limited computational resources of satellites’ processors. New guidance algorithms based on mean relative orbit elements will be studied to deal with knowledge and dynamical errors in complex deep-space environments. Unfortunately, questions remain whether similar derivations can be carried out for low-altitude QSOs, which is why future research will be focused on extending the applicability of the averaged approach near the surface of the target bodies.