Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part I—linear problem

Abstract

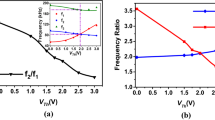
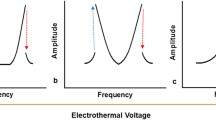
We investigate, experimentally and theoretically, the linear mode coupling between the first symmetric and antisymmetric modes of an electrothermally tuned and electrostatically actuated micromachined arch resonator. The arch is excited using an antisymmetric partial electrode to activate both modes of vibrations. Theoretically, we explore the static and dynamic behavior using the Galerkin method. When tuning the electrothermal voltage, the first symmetric frequency increases while the first antisymmetric frequency decreases until they cross. The results show linear coupling and hybridization of both modes near crossing only in the presence of the perturbation from the electrostatic force using the partial electrode. We show the linear merging of both modes at crossing. Also, the eigenfrequency variation around crossing shows a ratio of 2:1 between the second symmetric mode and the first symmetric/antisymmetric modes, which can lead to simultaneous 1:1 and 2:1 internal resonances.

Appendix

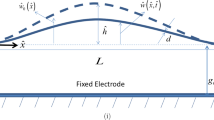
Here, we present the procedure of solving the eigenvalue problem of the arch beam when varying the electrothermal and the DC bias voltages. The static deflection of the arch beam, due to $V_\mathrm{Th}$ and $V_\mathrm{DC}$, is governed by

$$\begin{aligned}&\frac{\mathrm{d}^{4}w_s }{\mathrm{d}x^{4}}=\left( \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \right. \nonumber \\&\quad \left. \left[ {N+\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2}+2\frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] \mathrm{d}x} } \right] \right) \nonumber \\&\quad +\,\alpha _2 \frac{V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{2}}u(x-0.5) \end{aligned}$$

(A.1)

with the associated boundary conditions

$$\begin{aligned} w_s (0)=w_s (1)=0\hbox { and }\left. {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right| _{x=0} =\left. {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right| _{x=1} =0\nonumber \\ \end{aligned}$$

(A.2)

To solve the eigenvalue problem, we drop the AC bias voltage and the damping terms from the equation of motion (Eq. (8)). Next, we assume that the total deflection is the sum of the static configuration, $w_{s}(x)$, and a small dynamic deflection of the arch beam, $w_{d}(x,t)$, around $w_{s}(x)$. The linearized equation of motion describing $w_{d}(x,t)$ is derived by substituting $w(x,t)=w_{d}(x,t)+w_{s}(x)$ into Eq. (8) and dropping the terms representing the equilibrium position and the nonlinear terms. This yields

$$\begin{aligned}&\frac{\partial ^{2}w_d }{\partial t^{2}}+\frac{\partial ^{4}w_d }{\partial x^{4}}\nonumber \\&\quad =\left[ {N+\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2}+2\frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] dx} } \right] \frac{\partial ^{2}w_d }{\partial x^{2}} \nonumber \\&\quad \quad +\,2\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}+\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right) \frac{\partial w_d }{\partial x}} \right] \mathrm{d}x} \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \nonumber \\&\quad \quad +\,2\alpha _2 \frac{V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{3}}u(x-0.5)w_d \end{aligned}$$

(A.3)

with the associated boundary conditions

$$\begin{aligned}&w_d (0,t)=w_d (1,t)=0\nonumber \\&\quad \hbox { and }\left. {\frac{\partial w_d }{\partial x}} \right| _{x=0,t} =\left. {\frac{\partial w_d }{\partial x}} \right| _{x=1,t} =0 \end{aligned}$$

(A.4)

We solve the eigenvalue problem of the arch beam under electrothermal voltage and electrostatic voltage [15, 34] by using the Galerkin discretization. Toward this, we let

$$\begin{aligned} w_d (x,t)=\sum _{i=0}^n {u_i (t)\varphi _i (x)} \end{aligned}$$

(A.5)

where $u_{i}{(t) (i=0,1,2\ldots n)}$ denotes the nondimensional modal coordinates and ${\varphi }_{i}(x) (i=0,1,2\ldots n)$ denotes the mode shape of the unactuated clamped–clamped arch beam. Next, we substitute Eq. (A.5) into Eq. (A.3), multiply the outcome by the mode shape ${\varphi }_{j}$ and integrate over the beam domain (from 0 to 1), which yield the below equation [15, 34]:

$$\begin{aligned} \ddot{u}_j= & {} -\int _0^1 {\varphi _j \left( {\sum _{i=0}^n {u_i \varphi _i ^{(iv)}} } \right) } \mathrm{d}x \nonumber \\&+\left[ N+\alpha _1 \int _0^1 \left[ \left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2} \right. \right. \nonumber \\&+\,2\left. \left. \frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x} \right] \mathrm{d}x \right] \int _0^1 {\varphi _j \left( {\sum _{i=0}^n {u_i \varphi _i {\prime }{\prime }} } \right) } \mathrm{d}x \nonumber \\&+\,2\alpha _1 \int _0^1 {\left[ {\left( {\frac{dw_s }{\mathrm{d}x}+\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right) \sum _{i=0}^n {u_i \varphi _i {\prime }} } \right] \mathrm{d}x} \nonumber \\&\quad \quad \int _0^1 {\varphi _j \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \mathrm{d}x} \nonumber \\&+\int _0^1 {\varphi _j \frac{2\alpha _2 V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{3}}\left( {\sum _{i=0}^n {u_i \varphi _i } } \right) u(x-0.5)\mathrm{d}x}\nonumber \\ \end{aligned}$$

(A.6)

Using four modes, we compute the Jacobian of the system of the four obtained equations, for each $V_\mathrm{Th}$ and $V_\mathrm{DC}$, and find the corresponding eigenvalues and eigenvectors (new mode shapes). Then, we compute the natural frequencies of the resonators, at constant $V_\mathrm{Th}$ and $V_\mathrm{DC}$, by taking the square root of these eigenvalues.