Skip to main content
SpringerLink
Log in

A high-order nonlinear Schrödinger equation as a variational problem for the averaged Lagrangian of the nonlinear Klein–Gordon equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

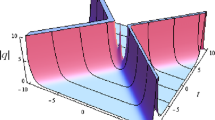
We use Whitham’s averaged Lagrangian method extended with the multiple-scale formalism to derive a sixth-order nonlinear Schrödinger equation for the complex amplitude of the envelope of the slowly modulated wave trains whose evolution is governed by the nonlinear Klein–Gordon equation with polynomial nonlinearity. Such a high-order nonlinear Schrödinger equation is obtained as a variational problem for the Lagrangian averaged over the rapid oscillations of the carrier wave train. As compared to classical Whitham’s approach, we take into account the derivatives of the complex amplitude with respect to slow timescales and long coordinate in the averaged Lagrangian. The coefficients of the high-order nonlinear Schrödinger equation derived in this work identically coincide with those derived by us earlier by the method of multiple scales applied directly to the original nonlinear Klein–Gordon equation. Finally, we consider the sine-Gordon equation as a partial case of the nonlinear Klein–Gordon equation and demonstrate one example of the numerical solution to the corresponding sixth-order nonlinear Schrödinger equation in the form of the envelope quasi-soliton.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Polyanin, A.D., Zaitsev, V.F.: Handbook of Nonlinear Partial Differential Equations, 2nd edn. CRC Press, Boca Raton (2012)

    MATH  Google Scholar 

  2. Scott, A. (ed.): Encyclopedia of Nonlinear Science. Routledge, New York (2005)

    MATH  Google Scholar 

  3. Nayfeh, A.H.: Perturbation Methods. Wiley, New York (1973)

    MATH  Google Scholar 

  4. Dodd, R.K., Eilbeck, J.C., Gibbon, J.D., Morris, H.C.: Solitons and Nonlinear Wave Equations. Academic, London (1982)

    MATH  Google Scholar 

  5. Agrawal, G.P.: Nonlinear Fiber Optics, 5th edn. Academic, Oxford (2013)

    MATH  Google Scholar 

  6. Kivshar, Yu.S., Agrawal, G.P.: Optical Solitons: From Fibers to Photonic Crystals. Academic, San Diego (2003)

    Chapter  Google Scholar 

  7. Ankiewicz, A., Wang, Y., Wabnitz, S., Akhmediev, N.: Extended nonlinear Schrödinger equation with higher-order odd and even terms and its rogue wave solutions. Phys. Rev. E 89, 012907 (2014)

    Article  Google Scholar 

  8. Ankiewicz, A., Kedziora, D.J., Chowdury, A., Bandelow, U., Akhmediev, N.: Infinite hierarchy of nonlinear Schrödinger equations and their solutions. Phys. Rev. E 93, 012206 (2016)

    Article  MathSciNet  Google Scholar 

  9. Sedletsky, Yu.V., Gandzha, I.S.: A sixth-order nonlinear Schrödinger equation as a reduction of the nonlinear Klein–Gordon equation for slowly modulated wave trains. Nonlinear Dyn. 94, 1921–1932 (2018)

    Article  Google Scholar 

  10. Kodama, Y., Hasegawa, A.: Nonlinear pulse propagation in a monomode dielectric guide. IEEE J. Quant. Electr. 23, 510–524 (1987)

    Article  Google Scholar 

  11. Zakharov, V.E., Kuznetsov, E.A.: Optical solitons and quasisolitons. JETP 86, 1035–1046 (1998)

    Article  Google Scholar 

  12. Gandzha, I.S., Sedletsky, Yu.V., Dutykh, D.S.: High-order nonlinear Schrödinger equation for the envelope of slowly modulated gravity waves on the surface of finite-depth fluid and its quasi-soliton solutions. Ukr. J. Phys. 59(12), 1201–1215 (2014)

    Article  Google Scholar 

  13. Craig, W., Guyenne, P., Sulem, C.: A Hamiltonian approach to nonlinear modulation of surface water waves. Wave Motion 47, 552–563 (2010)

    Article  MathSciNet  Google Scholar 

  14. Gramstad, O., Trulsen, K.: Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth. J. Fluid Mech. 670, 404–426 (2011)

    Article  MathSciNet  Google Scholar 

  15. Dysthe, K.B.: Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A 369, 105–114 (1979)

    Article  Google Scholar 

  16. Craig, W., Guyenne, P., Sulem, C.: Hamiltonian higher-order nonlinear Schrödinger equations for broader-banded waves on deep water. Eur. J. Mech. B 32, 22–31 (2012)

    Article  MathSciNet  Google Scholar 

  17. Borich, M.A., Kobelev, A.V., Smagin, A.V., Tankeyev, A.P.: Evolution of the surface magnetostatic wave envelope solitons in a ferromagnetic-dielectric-metal structure. J. Phys. Condens. Matter. 15, 8543–8559 (2003)

    Article  Google Scholar 

  18. Tsitsas, N.L., Rompotis, N., Kourakis, I., Kevrekidis, P.G., Frantzeskakis, D.J.: Higher-order effects and ultrashort solitons in left-handed metamaterials. Phys. Rev. E 79, 037601 (2009)

    Article  Google Scholar 

  19. Lü, X., Ma, W.-X., Yu, J., Khalique, C.M.: Solitary waves with the Madelung fluid description: a generalized derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 31, 40–46 (2016)

    Article  MathSciNet  Google Scholar 

  20. Sulem, C., Sulem, P.-L.: The Nonlinear Schrödinger Equation, Self-focusing and Wave Collapse. Springer, New York (1999)

    MATH  Google Scholar 

  21. Whitham, G.B.: Non-linear dispersion of water waves. J. Fluid Mech. 27, 399–412 (1967)

    Article  MathSciNet  Google Scholar 

  22. Whitham, G.B.: Two-timing, variational principles and waves. J. Fluid Mech. 44, 373–395 (1970)

    Article  MathSciNet  Google Scholar 

  23. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  24. Yuen, H.C., Lake, B.M.: Nonlinear deep water waves: theory and experiment. Phys. Fluids 18, 956–960 (1975)

    Article  Google Scholar 

  25. Sedletsky, Yu.V.: Addition of dispersive terms to the method of averaged Lagrangian. Phys. Fluids 24, 062105 (2012)

    Article  Google Scholar 

  26. Sedletsky, Yu.V.: Inclusion of dispersive terms in the averaged Lagrangian method: turning to the complex amplitude of envelope. Nonlinear Dyn. 81, 383–393 (2015)

    Article  MathSciNet  Google Scholar 

  27. Zakharov, V.E.: The Hamiltonian formalism for waves in nonlinear media having dispersion. Radiophys. Quantum Electron. 17(4), 326–343 (1974)

    Article  Google Scholar 

  28. Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of deep fluid. J. Appl. Mech. Tech. Phys. 9(2), 190–194 (1968)

    Article  Google Scholar 

  29. Stiassnie, M., Shemer, L.: On modifications of the Zakharov equation for surface gravity waves. J. Fluid Mech. 143, 47–67 (1984)

    Article  MathSciNet  Google Scholar 

  30. Gramstad, O.: The Zakharov equation with separate mean flow and mean surface. J. Fluid Mech. 740, 254–277 (2014)

    Article  MathSciNet  Google Scholar 

  31. Dyachenko, A.I., Lushnikov, P.M., Zakharov, V.E.: Non-canonical Hamiltonian structure and Poisson bracket for two-dimensional hydrodynamics with free surface. J. Fluid Mech. 869, 526–552 (2019)

    Article  MathSciNet  Google Scholar 

  32. Lukomsky, V.P., Gandzha, I.S.: Two-parameter method for describing the nonlinear evolution of narrow-band wave trains. Ukr. J. Phys. 54(1–2), 207–215 (2009)

    Google Scholar 

  33. Selezov, I.T., Kryvonos, Yu.G., Gandzha, I.S.: Spectral methods in the theory of wave propagation and diffraction. In: Wave Propagation and Diffraction: Mathematical Methods and Applications. Springer, Singapore (2018). Chap. 2

  34. Scott, A.C.: A nonlinear Klein–Gordon equation. J. Math. Phys. 37, 52–61 (1969)

    Google Scholar 

  35. Wazwaz, A.M.: The tanh and the sine–cosine methods for compact and noncompact solutions of the nonlinear Klein–Gordon equation. Appl. Math. Comp. 167, 1179–1195 (2005)

    Article  MathSciNet  Google Scholar 

  36. Cuevas-Maraver, J., Kevrekidis, P.G., Williams, F. (eds.): The sine-Gordon Model and Its Applications: From Pendula and Josephson Junctions to Gravity and High-Energy Physics. Springer, New York (2014)

    MATH  Google Scholar 

  37. Dehghan, M., Shokri, A.: A numerical method for solution of the two-dimensional sine–Gordon equation using the radial basis functions. Math. Comput. Simul. 79, 700–715 (2008)

    Article  MathSciNet  Google Scholar 

  38. Dehghan, M., Shokri, A.: Numerical solution of the nonlinear Klein–Gordon equation using radial basis functions. J. Comput. Appl. Math. 230, 400–410 (2009)

    Article  MathSciNet  Google Scholar 

  39. Sassaman, R., Biswas, A.: Topological and non-topological solitons of the Klein–Gordon equations in \(1+2\) dimensions. Nonlinear Dyn. 61, 23–28 (2010)

    Article  MathSciNet  Google Scholar 

  40. Gelfand, I.M., Fomin, S.V.: Calculus of Variations. Prentice-Hall, Englewood Cliffs (1963)

    MATH  Google Scholar 

  41. Bridges, T.J.: Breakdown of the Whitham modulation theory and the emergence of dispersion. Stud. Appl. Math. 135, 277–294 (2015)

    Article  MathSciNet  Google Scholar 

  42. Bridges, T.J., Ratliff, D.J.: On elliptic-hyperbolic transition in Whitham modulation theory. SIAM J. Appl. Math. 77, 1989–2011 (2017)

    Article  MathSciNet  Google Scholar 

  43. Bridges, T.J.: Symmetry, Phase Modulation and Nonlinear Waves. Cambridge University Press, New York (2017)

    Book  Google Scholar 

  44. Chowdury, A., Kedziora, D.J., Ankiewicz, A., Akhmediev, N.: Soliton solutions of an integrable nonlinear Schrödinger equation with quintic terms. Phys. Rev. E 90, 032922 (2014)

    Article  Google Scholar 

  45. Chowdury, A., Kedziora, D.J., Ankiewicz, A., Akhmediev, N.: Breather-to-soliton conversions described by the quintic equation of the nonlinear Schrödinger hierarchy. Phys. Rev. E 91, 032928 (2015)

    Article  MathSciNet  Google Scholar 

  46. Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34(1), 62–69 (1972)

    MathSciNet  Google Scholar 

  47. Sharma, A.S., Buti, B.: Envelope solitons and holes for sine–Gordon and non-linear Klein–Gordon equations. J. Phys. A Math. Gen. 9(11), 1823–1826 (1976)

    Article  MathSciNet  Google Scholar 

  48. Karpman, V.I., Rasmussen, J.J., Shagalov, A.G.: Dynamics of solitons and quasisolitons of the cubic third-order nonlinear Schrödinger equation. Phys. Rev. E 64, 026614 (2001)

    Article  Google Scholar 

Download references

Acknowledgements

Dr. Ivan Gandzha is grateful to Wolfram Research for providing him with a free contemporary licence for the use of Mathematica 12.

Author information

Authors and Affiliations

  1. Institute of Physics, National Academy of Sciences of Ukraine, Prosp. Nauky 46, Kyiv, 03028, Ukraine

    Ivan S. Gandzha & Yuri V. Sedletsky

Authors
  1. Ivan S. Gandzha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuri V. Sedletsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ivan S. Gandzha.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gandzha, I.S., Sedletsky, Y.V. A high-order nonlinear Schrödinger equation as a variational problem for the averaged Lagrangian of the nonlinear Klein–Gordon equation. Nonlinear Dyn 98, 359–374 (2019). https://doi.org/10.1007/s11071-019-05197-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05197-x

Keywords

Search

Navigation