Skip to main content
SpringerLink
Log in

Security performance analysis of a chaotic stream cipher

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

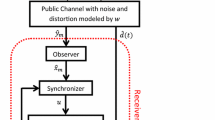
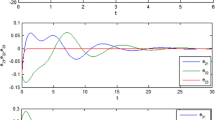
In this paper, the security performance analysis for a self-synchronization and closed-loop feedback-based chaotic stream cipher is given. According to the chosen-ciphertext attack method, it is found that under the condition of selecting the ciphertext as fixed value, the original chaotic iterative equation is degenerated into an asymptotically stable iterative one, so that the explicit function of state variables and key parameters can be obtained. Based on this idea, and according to the chosen-ciphertext attack method, a single key decipher algorithm is further investigated. Firstly, multiple pairs of plaintext–ciphertext are obtained by choosing the corresponding multiple frames of ciphertext as fixed values. Secondly, a set of possible estimated values for this single key is acquired by utilizing among one pair of plaintext–ciphertext. Finally, the only estimated value that satisfies all the conditions of multiple pairs of plaintext–ciphertext is determined, as an estimated value from the set of all possible estimated values. Security performance analysis results have shown that, under the condition that only one unknown key needs to be deciphered while the remaining keys are all known, the proposed algorithm can, respectively, decipher each individual key accurately. In addition, the attack complexity of the proposed method is lower than that of the exhaustive attack.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Chen, Z., Yuan, X., Yuan, Y., Iu, H.H.C., Fernando, T.: Parameter identification of chaotic and hyper-chaotic systems using synchronization-based parameter observer. IEEE Trans. Circuits Syst. I Regul. Pap. 63(9), 1464–1475 (2016)

    Article  MathSciNet  Google Scholar 

  2. Gan, Q., Yu, S., Li, C., Lü, J., Lin, Z., Chen, P.: Design and ARM-embedded implementation of a chaotic map-based multicast scheme for multiuser speech wireless communication. Int. J. Circuit Theory Appl. 45, 1849–1872 (2017)

    Article  Google Scholar 

  3. Gao, F., Tong, H.Q.: Parameter estimation for chaotic system based on particle swarm optimization. Acta Physica Sin. 55(2), 577–582 (2006)

    Google Scholar 

  4. Gao, T., Chen, Z.: A new image encryption algorithm based on hyper-chaos. Phys. Lett. A 372(4), 394–400 (2008)

    Article  MATH  Google Scholar 

  5. Hu, G., Feng, Z., Ruiling, M.: Chosen ciphertext attack on chaos communication based on chaotic synchronization. IEEE Trans. Circuits and Syst. I: Fundam. Theory Appl. 50(2), 275–279 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kerckhoffs, A.: La cryptographie militaire. J. Des Sci. Mil. 9, 5–83 (1883)

    Google Scholar 

  7. Li, C., Chen, G.: On the security of a class of image encryption schemes. In: 2008 IEEE International Symposium on Circuits and Systems, pp. 3290–3293. IEEE (2008)

  8. Li, C., Liu, Y., Zhang, L.Y., Chen, M.Z.: Breaking a chaotic image encryption algorithm based on modulo addition and xor operation. Int. J. Bifurc. Chaos 23(04), 1350075 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Li, C., Lo, K.T.: Optimal quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks. Sig. Process. 91(4), 949–954 (2011)

    Article  MATH  Google Scholar 

  10. Li, S., Li, C., Chen, G., Bourbakis, N.G., Lo, K.T.: A general quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks. Sig. Process. Image Commun. 23(3), 212–223 (2008)

    Article  Google Scholar 

  11. Lin, Z., Yu, S., Lü, J., Cai, S., Chen, G.: Design and arm-embedded implementation of a chaotic map-based real-time secure video communication system. IEEE Trans. Circuits Syst. Video Technol. 25(7), 1203–1216 (2015)

    Article  Google Scholar 

  12. Lü, J., Chen, G.: A new chaotic attractor coined. Int. J. Bifurc. Chaos 12(03), 659–661 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Matthews, R.: On the derivation of a “chaotic” encryption algorithm. Cryptologia 13(1), 29–42 (1989)

    Article  MathSciNet  Google Scholar 

  14. Rao, K.D.D., Gangadhar, C.: Modified chaotic key-based algorithm for image encryption and its VLSI realization. In: 15th International Conference on Digital Signal Processing, pp. 439–442. IEEE (2007)

  15. Van Den Bergh, F.: An analysis of particle swarm optimizers. Ph.D. thesis, University of Pretoria (2007)

  16. Wang, J., Jiang, G.: Cryptanalysis of a hyper-chaotic image encryption algorithm and its improved version. Acta Physica Sin. 60(6), 83–93 (2011)

    MATH  Google Scholar 

  17. Wang, L., He, W.P., Wan, S.Q., Liao, L.J., He, T., Center, N.C.: Evolutionary modeling for parameter estimation for chaotic system. Acta Physica Sin. 63(1), 247–254 (2014)

    Google Scholar 

  18. Wu, C.W., Chua, L.O.: A simple way to synchronize chaotic systems with applications to secure communication systems. Int. J. Bifurc. Chaos 3(06), 1619–1627 (1993)

    Article  MATH  Google Scholar 

  19. Xu, Y., Zhou, W., Fang, J., Sun, W.: Adaptive lag synchronization and parameters adaptive lag identification of chaotic systems. Phys. Lett. A 374(34), 3441–3446 (2010)

    Article  MATH  Google Scholar 

  20. Yen, J., Guo, J.: Efficient hierarchical chaotic image encryption algorithm and its vlsi realisation. IEE Proc.-Vision, Image Signal Process. 147(2), 167–175 (2000)

    Article  Google Scholar 

  21. Yu, S., Lü, J., Li, C.: Some progresses of chaotic cipher and its applications in multimedia secure communications. J. Electron. Inf. Technol. 38(3), 735–752 (2016)

    Google Scholar 

  22. Zhu, C., Sun, K.: Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms. Acta Physica Sin. 61(12), 76–87 (2012)

    MATH  Google Scholar 

Download references

Funding

This work was supported by the National Key Research and Development Program of China (No. 2016YFB0800401), and the National Natural Science Foundation of China (Nos. 61771176, 61401134, 61532020, 61671161).

Author information

Authors and Affiliations

  1. School of Electronics and Information, Hangzhou Dianzi University, Hangzhou, 310018, China

    Zhuosheng Lin, Guangyi Wang, Xiaoyuan Wang & Simin Yu

  2. College of Automation, Guangdong University of Technology, Guangzhou, 510006, China

    Zhuosheng Lin & Simin Yu

  3. Institute of Systems Science, Academy of Mathematics and Systems Sciences, Chinese Academy of Sciences, Beijing, 100190, China

    Jinhu Lü

Authors
  1. Zhuosheng Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guangyi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaoyuan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Simin Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jinhu Lü
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guangyi Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Z., Wang, G., Wang, X. et al. Security performance analysis of a chaotic stream cipher. Nonlinear Dyn 94, 1003–1017 (2018). https://doi.org/10.1007/s11071-018-4406-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4406-8

Keywords

Search

Navigation