Two-parameter bifurcation analysis of limit cycles of a simplified railway wheelset model

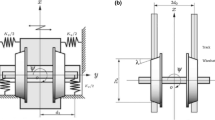
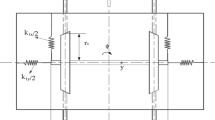
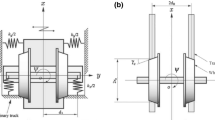
Abstract

The effect of the nonlinear terms on bifurcation behaviors of limit cycles of a simplified railway wheelset model is investigated. At first, the stable equilibrium state loses its stability via a Hopf bifurcation. The bifurcation curve is divided into a supercritical branch and a subcritical one by a generalized Hopf point, which plays a key role in determining the occurrence of flange contact and derailment of high-speed railway vehicles, and the occurrence of this critical situation is an important decision-making criteria for design parameters. Secondly, bifurcations of limit cycles are discussed by comparing the bifurcation behavior of cycles for two different nonlinear parameters. Unlike local Hopf bifurcation analysis based on a single bifurcation parameter in most papers, global bifurcation analysis of limit cycles based on two bifurcation parameters is investigated, simultaneously. It is shown that changing nonlinear parameter terms can affect bifurcation types of cycles and division of parameter domains. In particular, near the branch points of cycles, two symmetrical limit cycles are created by a pitchfork bifurcation and then two symmetrical cycles both undergo a period-doubling bifurcation to form two stable period-two cycles. Around the resonant points, period orbits can make several turns, whose number of turns corresponds to the ratio of resonance. Thirdly, near the Neimark–Sacker bifurcation of cycles, a stable torus is created by a supercritical Neimark–Sacker bifurcation, which shows that the orbit of the model exhibits modulated oscillations with two frequencies near the limit cycle. These results demonstrate that nonlinear parameter terms can produce very complex global bifurcation phenomena and make obvious effects on possible hunting motions even though a simple railway wheelset model is concerned.

Appendix

$$\begin{aligned} A_{21}= & {} -\frac{3d^3_{22}}{\bar{\tau } k^3_{21}}\left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}+i\frac{\omega }{v^*}\right) \\&\times \left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}-i\frac{\omega }{v^*} \right) ^2\alpha _{yyy}\\&-\,\frac{d^2_{22}}{\bar{\tau } k^2_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2}+\frac{\omega ^2}{v^{*2}}\right. \\&\left. -\,i\frac{2\omega (k_{11}-k_{22}+k_{a11})}{(d_{11}+d_{22})v^{*}}\right) \alpha _{yy\psi }\\&-\,\frac{d_{22}}{\bar{\tau } k_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})}{d_{11}+d_{22}}-i\frac{\omega }{v^{*}}\right) \alpha _{y\psi \psi }\\&-\frac{3}{\bar{\tau }}\alpha _{\psi \psi \psi }\\&+\,\frac{3 d_{11}d^3_{22}\left( (k_{11}-k_{22}+k_{a11})^2v^{*2}+\omega ^2(d_{11}+d_{22})^2\right) ^2}{ \tau (k_{21}v^{*})^4(d_{11}+d_{22})^4 }\beta _{yyy}\\&+\,\frac{d_{11}d^2_{22}}{\bar{\tau } k^3_{21}}\left( \frac{(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2} +\frac{\omega ^2}{v^{*2}}\right) \\&\times \left( \frac{3(k_{11}-k_{22}+k_{a11})}{d_{11}+d_{22}}+i\frac{\omega }{v^{*}}\right) \beta _{yy\psi }\\&+\,\frac{d_{11}d_{22}}{\bar{\tau } k^2_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2}\right. \\&\left. +\,\frac{\omega ^2}{v^{*2}}+ i\frac{2\omega (k_{11}-k_{22}+k_{a11})}{(d_{11}+d_{22})v^{*}}\right) \beta _{y\psi \psi }\\&+\,\frac{3d_{11}}{\bar{\tau } k_{21}}\left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}+i\frac{\omega }{v^{*}}\right) \beta _{\psi \psi \psi }, \end{aligned}$$

$$\begin{aligned}&l_{1}(k_{a11},v^*)=\left[ \left( 2265k^5_{a11}-2379.1k^4_{a11} +789.17k^3_{a11}\right. \right. \\&\quad \qquad \qquad \qquad \left. \left. -\,46.093k^2_{a11}-30.711k_{a11}+0.8893\right) v^{*4}\right. \\&+\,\left( 120{,}500k^4_{a11}-51{,}814k^3_{a11}-6779.5k^2_{a11}\right. \\&\left. +1550.7k_{a11}+140.13\right) v^{*2}\\&+\,\left( 0.6474k_{a11}+0.1006\right) ^{\frac{3}{2}} \left( 0.399+2.5689k_{a11}\right) v^{*}\\&+\,1{,}602{,}800k^3_{a11}+305{,}210k^2_{a11}\\&-\,\left. 21{,}188k_{a11}-4648.3\right] \!{\big /} \!\left\{ \!\left[ \left( k^3_{a11}-0.2688k^2_{a11}\right. \right. \right. \\&\left. \left. \left. -\,0.021k_{a11}+0.007\right) v^{*5}+\left( 98.661k_{a11}\right. \right. \right. \\&+\,\left. \left. \left. 9.4776+242.36k_{a11}^2\right) v^{*3}\right. \right. \\&\left. \left. +\,\left( 157.15+1011.8k_{a11}\right) v^{*}\right] \sqrt{0.6474k_{a11}+0.1006}\right\} . \end{aligned}$$