1 Introduction

Many natural phenomena and engineering processes exhibit energy transfer among a range of different scales. The simplest, frequently studied examples of energy transfer are linear and nonlinear chain oscillators [1,2,3,4,5,6,7] . Dissipation is a key feature of such systems. Jiang et al. [8] and Tripathi et al. [9] investigated and compared the performance of nonlinear energy sink (light mass with viscous damping and an essentially nonlinear spring attached to the primary system) and linear tuned mass damper on multi-degree-of-freedom systems. Felix et al. [10] studied energy pumping and the beat phenomenon in a nonideal oscillator attached to a nonlinear energy sink. Pumhössel found a method to effectively transfer energy among vibration modes using impulsive force excitations [11]. Liu and Jing [12] proposed an X-shaped structure which has advantageous vibrational energy harvesting performance.

Turbulent flow is a prime example of a process which exhibits different scales and an energy cascade. Richardson’s so-called eddy hypothesis [13, 14] argues that the largest eddies are unstable and break up forming several smaller vortices, gradually transferring the kinetic energy of the flow to smaller scales.

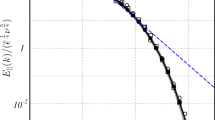
The turbulent energy cascade is characterized by the energy spectrum \({\hat{E}}(\kappa )\) which describes the distribution of the total energy \(E=\int {\hat{E}}(\kappa )\mathrm{d}\kappa \) among the different scales. The wavenumber \(\kappa \sim 1/L\) is associated with the vortex having characteristic size L. The Kolmogorov spectrum (Fig. 1) illustrates the main features of the turbulent energy cascade. It is the energy spectrum corresponding to 3D homogeneous isotropic turbulence assuming a forcing at the large scales [15,16,17]. The energy input mainly affects the large scales (characterized by \(L_{0}\)); hence, the bulk of the energy is contained in the large eddies (energy containing range). In the inertial range (intermediate wavenumbers \(1/L_{0}<\kappa <1/\eta \)), the energy spectrum is described by the famous Kolmogorov scaling law \({\hat{E}}(\kappa )\sim \kappa ^{-5/3}\) [15, 17]. The largest wavenumbers (\(\kappa >1/\eta \)) are associated with length scales smaller than the Kolmogorov length scale \(\eta \). This is the so-called dissipation range in which most kinetic energy is lost due to viscous friction. The Kolmogorov spectrum is confirmed by numerous measurements and simulations [18,19,20,21]. For turbulent flows, the energy flux \({\varPi }(\kappa )\) is also defined which shows the rate of energy transfer at the different wavenumbers \(\kappa \). For 3D homogeneous isotropic turbulence, the energy flux is constant: \({\varPi }(\kappa )=\epsilon \), where \(\epsilon =-\mathrm{d}E/\mathrm{d}t\) is the dissipation rate of the kinetic energy E.

Fig. 1
figure 1

Qualitative graph of the Kolmogorov spectrum

Full size image

Though energy cascades are usually related to nonlinear phenomena, infinite-dimensional linear systems can also contain a wide range of scales and exhibit complex behavior [22]. In fact, nonlinear systems can be embedded in infinite-dimensional linear systems [23].

Motivated by this, we asked the question: Is there a simple linear model whose energy spectrum has features similar to that of the Kolmogorov spectrum? To answer this question in the affirmative, we present a linear phenomenological model of turbulence inspired by Richardson’s cascade description. We show that this hierarchical model exhibits the characteristic spectrum of energy transfer seen in turbulent flows. This new point of view will hopefully stimulate research connecting eigenvalue distributions of infinite-dimensional linear systems with energy transfer and resonance capture in nonlinear systems. We also state what this model is NOT: It is not meant to explain details of turbulence; in fact, the behavior of the model is different in many aspects.

Although Fig. 1 corresponds to a process which includes continuous energy injection through forcing, our model freely decays its initial energy. There also exist decaying processes with Kolmogorov-like energy spectrum (see, e.g., [19, 24]). The energy decay in our model is exponential as opposed to the power law decrease by decaying turbulence, and the energy transfer is not reversible.

Our phenomenological model of vortex breakdown is a binary tree of masses and springs with dampers at the ground level (Fig. 2a shows a 3-level model). The masses represent the different scales, the springs are responsible for the energy transfer, and the dampers dissipate energy at the lowest scales. Finite-dimensional modeling of turbulence is common; see, e.g., shell models [17, 21] and low-dimensional modeling of turbulence with proper orthogonal decomposition [25]. A similar tree-structured linear mass–spring–damper system was used before to tackle other engineering problems, e.g., viscoelastic behavior [26] and damage detection [27]. It was shown in these papers that the infinite version of their system is described by a fractional (1 / 2th order) differential equation.

Fig. 2
figure 2

a The phenomenological model of vortex breakdown and b the equivalent chain oscillator

Full size image

In this paper, we intend to produce an energy spectrum similar to that observed in turbulent flows (Fig. 1) with a simple linear system. We define the scales, wavenumber, energy spectrum, and energy flux of our phenomenological model analogously to those of turbulent flow. In previous papers, we showed preliminary numerical results for the energy spectrum of decaying and forced systems [28] and an analytical derivation of the energy spectrum of our model [29]. We also performed numerical calculations on a nonlinear version of the model [30].

The main finding is that the energy spectrum exhibits the main features of the Kolmogorov spectrum shown in Fig. 1 for suitably chosen parameters. By fine-tuning of the parameters, the midrange of the energy spectrum also has the famous \(-5/3\) scaling exponent. Moreover, we also show how the energy spectrum of the model behaves for different parameters and how this is related to the self-similar structure of the model through the eigenvalues.

2 Mechanistic turbulence model

Our mechanistic model (Fig. 2a) has n levels, level \(l\in \left\{ 1,\ldots ,n\right\} \) consists of \(2^{l-1}\) masses, and the total number of masses is \(N=2^{n}-1\). The top mass and the bottom masses are connected to the fixed ceiling and ground, respectively. Every mass \(m_{i}\) has a parent and two (left and right) children whose indices are \({\mathcal {P}}(i)=\lfloor i/2\rfloor ,\ {\mathcal {L}}(i)=2i,\ {\mathcal {R}}(i)=2i+1\), respectively (\(i=1,\ldots ,N\)), where \(\lfloor .\rfloor \) denotes the floor operation.

The equations of motion are

$$\begin{aligned} \begin{aligned} m_{i}\ddot{x}_{i}&=k_{i}(x_{{\mathcal {P}}(i)}-x_{i})+k_{{\mathcal {L}} (i)}(x_{{\mathcal {L}}(i)}-x_{i}) \\&\quad +k_{{\mathcal {R}}(i)}(x_{{\mathcal {R}}(i)}-x_{i})+c_{i}({\dot{x}}_{{\mathcal {P}} (i)}-{\dot{x}}_{i}) \\&\quad +c_{{\mathcal {L}}(i)}({\dot{x}}_{{\mathcal {L}}(i)}-{\dot{x}}_{i})+c_{{\mathcal {R}} (i)}({\dot{x}}_{{\mathcal {R}}(i)} -{\dot{x}}_{i}),\\&\qquad i= 1,\ldots ,N, \end{aligned} \end{aligned}$$
(1)

with the boundary conditions (the ceiling and the ground are motionless) \(x_{i}=0,\ i=0,N+1,\ldots ,2N+1\). The initial conditions are \(x_{i}(0)=x_{i,0},\ {\dot{x}}_{i}(0)=v_{i,0},\ i=1,\ldots ,N.\) The matrix form of Eq. (1) is

$$\begin{aligned} {\mathcal {M}}\ddot{{\mathbf {x}}}+{\mathcal {C}}\dot{{\mathbf {x}}}+{\mathcal {K}} {\mathbf {{x}}}={\mathbf {0}},\quad {\mathbf {{x}}}(0)={\mathbf {{x}}}_{0},\quad \dot{{\mathbf {x}} }(0)={\mathbf {v}}_{0}, \end{aligned}$$
(2)

where \({\mathbf {{x}}}\) is the vector of displacements and \({\mathcal {M}}\), \({\mathcal {C}}\), and \({\mathcal {K}}\) are the mass, damping, and stiffness matrices, respectively.

2.1 Model parameters

We introduce a quantity analogous with the wavenumber of a turbulent scale, the “mass wavenumber”

$$\begin{aligned} \kappa _{l}=1/M_{l},\quad l=1,\ldots ,n. \end{aligned}$$
(3)

Here \(M_{l}\) is the mass scale representing masses in level l (average, for example). For the ease of exposition, we set every mass, stiffness, and damping coefficient equal within a level l and denote these with \(M_{l}\), \(K_{l}\), \(C_{l}\) (\(K_{l}\) and \(C_{l}\) refer to the springs and dampers connecting the masses of the \(l-1\)th and lth levels.). The masses are gradually decreased in lower levels, analogously to the eddy hypothesis, in which a large vortex breaks up into smaller ones. The mass scales \(M_{l}\) and the stiffnesses \(K_{l}\) are specified by power law distributions, while the dampings are tuned to the stiffnesses (by design, only \(C_{n+1}\) is nonzero), i.e.

$$\begin{aligned} \begin{aligned}&M_{l} =\left( \frac{1}{2}\right) ^{l-1},\quad l=1,\ldots ,n, \\&K_{l} =\sigma ^{l-1},\quad l=1,\ldots ,n+1, \\&C_{n+1}=2\sqrt{M_{n}K_{n+1}}=2^{\frac{3-n}{2}}\sigma ^{\frac{n}{2}}. \end{aligned} \end{aligned}$$
(4)

Thus, the sum of masses in each level is 1. The characteristics of the energy spectrum of the mechanistic model (defined in Sect. 4) mainly depend on the relation between the base parameters of Eq. (4) (1 / 2 and \(\sigma \)). This means that one such base parameter is enough to describe the behavior of the mechanistic model without the loss of generality.

3 The eigenvalue distribution

The eigenvalues of system (2) are the roots of the characteristic equation \(P(\lambda )=\det ({\mathcal {M}}\lambda ^{2}+{\mathcal {C}} \lambda +{\mathcal {K}})=0\).

Claim

The characteristic polynomial of the undamped n-level system (2) (\({\mathcal {C}}=0\)) with parameter \(\sigma =1/2\) has the form

$$\begin{aligned} \begin{aligned} P_{0}(\lambda )=&1,\,\,\,\,\, P_{n}(\lambda )=\frac{Q_{n}(\lambda )}{Q_{n-1}(\lambda )}P_{n-1}^{2}(\lambda ),\quad n>0. \end{aligned} \end{aligned}$$
(5)

Here \(Q_{i}(\lambda )\) are \(Q_{0}(\lambda )=1\),

$$\begin{aligned} Q_{i}(\lambda )=U_{i}\left( \frac{\lambda ^{2}+2}{2}\right) -\frac{1}{2}U_{i-1}\left( \frac{\lambda ^{2}+2}{2}\right) ,\quad i>0, \end{aligned}$$
(6)

where \(U_{i}\) denotes the ith Chebyshev polynomial of the second kind [31].

Figure 3 shows the eigenvalue distribution of the purely imaginary eigenvalues of system (2) for the undamped (\({\mathcal {C}}=0\)) case with 10 levels, \(\sigma =1/2\). This eigenvalue distribution exhibits a “devil’s staircase”-type self-similarity which is related to the self-similar structure of the mechanistic model (binary tree structure). He et al. [32] and Kalmár-Nagy et al. [33] reported different classes of self-similar graphs whose adjacency matrices have devil’s staircase-type spectrum. In the latter paper, it was also shown that the characteristic polynomial of the adjacency matrix is a product of Chebyshev polynomials. For damped systems (even for different \(\sigma \) values), the frequency distributions (the imaginary parts of the complex eigenvalues) exhibit similar fractal characteristics as that in Fig. 3.

Fig. 3
figure 3

Eigenvalue distribution of the conservative 10-level mechanistic model for \(\sigma =1/2\)

Full size image

4 The energy spectrum

For turbulent flows, the energy spectrum shows the “contribution” of the different scales of eddies to the total energy of the flow, i.e. the mean energy stored in the different wavenumbers \(\kappa \). An analogous energy spectrum is now defined for the mechanistic model showing the energy fraction stored in the different scales \(M_{\mathrm{l}}\) (the energy spectrum of the finite-sized mechanistic model is discrete).

The total mechanical energy E(t) of the system is

$$\begin{aligned} E(t)=\frac{1}{2}\dot{{\mathbf {{x}}}}^{T}(t){\mathcal {M}}\dot{{\mathbf {{x}}}}(t)+\frac{1}{2}{\mathbf {{x}}}^{T}(t){\mathcal {K}}{\mathbf {{x}}}(t). \end{aligned}$$
(7)

The total energy is simply the sum of level energies, i.e. \(E(t)=\sum _{l=1}^{n}E_{l}(t)\). \(E_{l}(t)\) is defined so that the potential energy of the springs connecting two masses is distributed equally between the two levels and the potential energy of the top and bottom springs is added to \(E_{1}(t)\) and \(E_{n}(t)\), respectively:

$$\begin{aligned} \begin{aligned} E_{l}(t)&=\frac{1}{2}M_{l}\sum \limits _{i\in I(l)}{\dot{x}}_{i}^{2} \\&\quad +\frac{1}{4}(1+\delta _{l,1})K_{l} \sum \limits _{i\in I(l)}{(x_{i} -x_{{\mathcal {P}}(i)})^{2}}\\&\quad +\frac{1}{4}(1+\delta _{l,n} )K_{l+1}\sum \limits _{i\in I(l+1)}{(x_{i} -x_{{\mathcal {P}}(i)})^{2}},\\&\qquad l=1,\ldots ,n. \end{aligned} \end{aligned}$$
(8)

Here, \(I(l)=\{2^{l-1},\ldots ,2^{l}-1\}\) are the indices on level l, and \(\delta \) is the Kronecker delta (\(\delta _{i,j}=1\) for \(i=j\), 0 otherwise). This definition of \(E_{l}(t)\) ensures its non-negativity for \(t\ge 0\).

Figure 4 shows E(t), \(E_{4}(t)\), \(E_{8}(t)\) of a 10-level mechanistic model with \(\sigma =1/2\) (launched from random initial conditions). The behavior of the energies \(E(t),E_{l}(t)\) (\(l=1,\ldots ,n\)) consists of a transient part and a decaying oscillatory state (the dashed lines in Fig. 4a are exponentially decaying functions with the same exponent). This is the characteristic behavior of E(t) and \(E_{l}(t)\) (\(l=1,\ldots ,n\)) as \(t\rightarrow \infty \).

Fig. 4
figure 4

aE(t), \(E_{4}(t)\), \(E_{8}(t)\) of a 10-level mechanistic model with \(\sigma =1/2\). b E(t) plotted for a narrow time interval

Full size image

The asymptotic behavior of the linear system (2)—and so of its energy—is determined by its rightmost pair of eigenvalues \(\lambda _{\mathrm{slow}},\ \lambda _{\mathrm{slow}}^{*}=\alpha \pm \beta i\) (corresponding to the slowest decaying motion, i.e. rightmost in the complex plane). Figure 4b shows how the real and imaginary parts of \(\lambda _{\mathrm{slow}},\ \lambda _{\mathrm{slow}}^{*}\) are related to the exponent and oscillation period of \(E(t), E_{l}(t)\): The exponent is \(2\alpha \), while the oscillation period is \(\pi /\beta \). We define the mean energy \({\bar{E}}\) in the asymptotic limit as

$$\begin{aligned} {\bar{E}}=\frac{\beta }{\pi }\int _{\tau }^{\tau +\pi /\beta }E(t)\mathrm{d}t,\quad \tau \rightarrow \infty , \end{aligned}$$
(9)

and we similarly define the mean level energy \({\bar{E}}_{l}\) for \(l=1,\ldots ,n\). The mean energy is simply the sum of the level energies, i.e. \({\bar{E}}=\sum _{l=1}^{n}{\bar{E}}_{l}\).

The energy fraction stored in mass wavenumber \(\kappa _{l}\) is defined as

$$\begin{aligned} {\hat{E}}_{l}={\bar{E}}_{l}/{\bar{E}},\quad l=1,\ldots ,n, \end{aligned}$$
(10)

and expresses the contribution of a scale \(M_{l}\) to the total energy of the system. The \({\hat{E}}_{l}\) values constitute the discrete energy spectrum \({\hat{E}}\) of the mechanistic model.

4.1 Derivation of the energy spectrum

A more detailed version of this derivation can be found in [29]. Equation (2) can be recast as a system of 2N first-order differential equations

$$\begin{aligned} \dot{{\mathbf {y}}}(t)=A{\mathbf {y}}(t),\quad {\mathbf {y}}(0)= {\mathbf {y}}_{0} \end{aligned}$$
(11)

with

$$\begin{aligned} \begin{aligned}&A= \begin{pmatrix} 0 &{} D_{1}^{*}D_{2}^{-*}\\ -D_{2}^{-1} D_{1} &{} -D_{2}^{-1}{\mathcal {C}}D_{2}^{-*} \end{pmatrix}, \\&{\mathbf {y}}(t) = \begin{pmatrix} D_{1}^{*}{\mathbf {{x}}}(t)\\ D_{2}^{*}\dot{{\mathbf {{x}}}}(t) \end{pmatrix}, \quad {\mathbf {y}}_{0}= \begin{pmatrix} D_{1}^{*}{\mathbf {{x}}}_{0}\\ D_{2}^{*}{\mathbf {v}}_{0} \end{pmatrix},\\&D_{1}D_{1}^{*}={\mathcal {K}},\quad D_{2}D_{2}^{*}={\mathcal {M}}, \end{aligned} \end{aligned}$$
(12)

where \(*\) and \(-*\) denote the conjugate transpose matrix and the inverse of the conjugate transpose matrix, respectively [34]. The solution \({\mathbf {y}}(t)\) of Eq. (11) is

$$\begin{aligned} {\mathbf {y}}(t)=e^{At}{\mathbf {y}}_{0}. \end{aligned}$$
(13)

The total energy of the system is

$$\begin{aligned} E(t)=\frac{1}{2}||{\mathbf {y}}(t)||^{2}=\frac{1}{2}{\mathbf {y}}_{0}^{T}e^{A^{*}t}e^{At}{\mathbf {y}}_{0}. \end{aligned}$$
(14)

Since we are interested in the asymptotic behavior of the system, only the terms related to the rightmost eigenvalue pair \(\lambda _{\mathrm{slow}},\ \lambda _{\mathrm{slow}}^{*}=\alpha \pm \beta i\) of A count in the solution of Eq. (11). All the other terms related to the other eigenvalues of A decay much faster and hence can be neglected. Thus, the general solution of Eq. (11) in the asymptotic limit \(t\rightarrow \infty \) is

$$\begin{aligned} {\mathbf {y}}(t)\cong e^{\alpha t}\big [{\mathbf {{b}}}_{1}\text {cos}(\beta t)+{\mathbf {{b}}}_{2}\text {sin}(\beta t)\big ], \end{aligned}$$
(15)

where \({\mathbf {{b}}}_{1},{\mathbf {{b}}}_{2}\) are constant vectors depending on the initial condition \({\mathbf {y}}_{0}\). Substituting Eq. (15) in Eq. (14) leads to

$$\begin{aligned} E(t)\cong e^{2\alpha t}\left[ B_{1}+B_{2}\text {cos}(2\beta t)+B_{3} \text {sin}(2\beta t)\right] , \end{aligned}$$
(16)

where \(B_{1}\), \(B_{2}\), and \(B_{3}\) are initial condition dependent constants. The decay \(2\alpha \) and the frequency \(2\beta \) are due to the quadratic form of (14). To perform the averaging in Eq. (9), we substitute Eq. (16) in Eq. (9). The result is

$$\begin{aligned} {\bar{E}}=\frac{e^{2\alpha \tau }\left( e^{2\alpha \frac{\pi }{\beta }}-1\right) }{2}\bigg (\frac{B_{1}}{\alpha }+\frac{\alpha B_{2}-\beta B_{3}}{\left( \alpha ^{2}+\beta ^{2}\right) }\bigg ). \end{aligned}$$
(17)

The mean level energies \({\bar{E}}_{l}\) have the same form as Eq. (17) with different constants \(B_{l,1}\), \(B_{l,2}\), \(B_{l,3}\) (\(l=1,\ldots ,n\)). The energy spectrum is obtained by substituting \({\bar{E}}\) and \({\bar{E}}_{l}\) in Eq. (10), i.e.

$$\begin{aligned} {\hat{E}}_{l}=\frac{(\alpha ^{2}+\beta ^{2})B_{l,1}+\alpha ^{2}B_{l,2}-\alpha \beta B_{l,3}}{(\alpha ^{2}+\beta ^{2})B_{1}+\alpha ^{2}B_{2}-\alpha \beta B_{3} }, \end{aligned}$$
(18)

\(l=1,\ldots ,n\). To calculate the coefficients \(B_{1},\ B_{2},\ B_{3}\), and \(B_{l,1},\ B_{l,2},\ B_{l,3}\), we specify the initial condition \({\mathbf {y}}_{0}\) in the two-dimensional “slow” subspace of the 2N-dimensional state space of Eq. (11). For example, we can take \({\mathbf {y}}_{0}=\text {{ Re} }{\mathbf {s}}_{\mathrm{slow}}\), where \({\mathbf {s}}_{\mathrm{slow}}\) is the eigenvector corresponding to \(\lambda _{\mathrm{slow}}\). For this initial condition, the evolution described by Eq. (16) is exact, i.e.

$$\begin{aligned} E(t)=e^{2\alpha t}\big [B_{1}+B_{2}\text {cos}(2\beta t)+B_{3}\text {sin}(2\beta t)\big ], \end{aligned}$$
(19)

for \(t\ge 0\). The unknown constants \(B_{1},\ B_{2},\ B_{3}\) can be computed from the system of algebraic equations

$$\begin{aligned} \begin{aligned} E(0)&=\frac{1}{2}{\mathbf {y}}_{0}^{T}{\mathbf {y}}_{0}=B_{1}+B_{2},\\ {\dot{E}}(0)&=\frac{1}{2}{\mathbf {y}}_{0}^{T}(A^{*}+A){\mathbf {y}}_{0} \\&=2\alpha B_{1}+2\alpha B_{2}+2\beta B_{3}, \\ {\ddot{E}}(0)&=\frac{1}{2}{\mathbf {y}}_{0}^{T}(A^{*2}+2A^{*}A+A^{2} ){\mathbf {y}}_{0} \\&=4\alpha ^{2}B_{1}+(4\alpha ^{2}-4\beta ^{2})B_{2}+8\alpha \beta B_{3}, \end{aligned} \end{aligned}$$
(20)

created by taking the first and second derivatives of the RHS of Eqs. (14), (19) at \(t=0\). We can calculate the initial values \(E(0),\ {\dot{E}}(0),\ {\ddot{E}}(0)\) from the initial condition \({\mathbf {y}}_{0}\). The solution of Eq. (20) is

$$\begin{aligned} \begin{pmatrix} B_{1}\\ B_{2}\\ B_{3} \end{pmatrix} =\frac{1}{4\beta ^{2}} \begin{pmatrix} 4(\alpha ^{2}+\beta ^{2}) &{} -4\alpha &{} 1\\ -4\alpha ^{2} &{} 4\alpha &{} -1\\ -4\alpha \beta &{} 2\beta &{} 0 \end{pmatrix} \begin{pmatrix} E(0)\\ {\dot{E}}(0)\\ {\ddot{E}}(0) \end{pmatrix} . \end{aligned}$$
(21)

The constants \(B_{l,1},\ B_{l,2},\ B_{l,3}\) (\(l=1,\ldots ,n\)) are calculated similarly. Substituting these solutions in Eq. (18) leads to

$$\begin{aligned} {\hat{E}}_{l}=\frac{{\ddot{E}}_{l}(0)-6\alpha {\dot{E}}_{l}(0)+4E_{l}(0)\left( 3\alpha ^{2}+\beta ^{2}\right) }{{\ddot{E}}(0)-6\alpha {\dot{E}}(0)+4E(0)\left( 3\alpha ^{2}+\beta ^{2}\right) }. \end{aligned}$$
(22)

Even though we can now compute the energy spectrum, its calculation is only feasible for relatively low number (order 10) of levels due to the rapidly increasing size of matrix A (an additional level almost doubles the number of masses). To overcome this issue, we reduce the mechanistic model by replacing entire levels of masses with single representative masses which leads to an equivalent chain oscillator.

5 The equivalent chain oscillator

Our approach is similar in spirit to renormalization techniques [35]. Renormalization group theory is extensively used to decimate the elements of large vibrational systems/chain oscillators [36, 37]. Figure 2b shows the equivalent chain oscillator which should exhibit the same energy spectrum (the energy distribution among the masses in the chain) as the hierarchical model shown in Fig. 2a. The elements of the mechanistic model are connected in parallel within a level; thus, it can be shown (see Eq. 4) that the parameters of the equivalent chain oscillator are

$$\begin{aligned} \begin{aligned}&M_{l}^{\prime }=2^{l-1}M_{l}=1,\quad l=1,\ldots ,n, \\&K_{l}^{\prime }=2^{l-1}K_{l},\quad l=1,\ldots ,n,\\&K_{n+1}^{\prime }=2^{n-1}K_{n+1},\\&C_{n+1}^{\prime }=2^{n-1}C_{n+1}. \end{aligned} \end{aligned}$$
(23)

The matrix form of the equations of motion is

$$\begin{aligned} \ddot{{\mathbf {z}}}+{\mathcal {C}}^{\prime }\dot{{\mathbf {{z}}}}+{\mathcal {K}}^{\prime }{\mathbf {{z}}}={\mathbf {0}},\quad {\mathbf {{z}}}(0)={\mathbf {{z}}}_{0},\quad \dot{{\mathbf {z}} }(0)={\mathbf {u}}_{0}. \end{aligned}$$
(24)

Figure 5 depicts the eigenvalues of a 10-level mechanistic model (\(\lambda _{i}\)) and those of its equivalent chain oscillator (\(\nu _{i}\)) with \(\sigma =1/2\).

Fig. 5
figure 5

Eigenvalues \(\lambda _{i}\) and \(\nu _{i}\) of 10-level systems for \(\sigma =1/2\)

Full size image

Claim

The characteristic polynomial of the undamped system (24) (\({\mathcal {C}}^{\prime }=0\)) with n masses and parameter \(\sigma =1/2\) is

$$\begin{aligned} Q_{n}(\nu )=U_{n}\left( \frac{\nu ^{2}+2}{2}\right) -\frac{1}{2}U_{n-1}\left( \frac{\nu ^{2}+2}{2}\right) , \end{aligned}$$
(25)

where \(U_{n}\) denotes the nth Chebyshev polynomial of the second kind (as in Eq. 6 of the first claim).

Figure 5 and our two claims (Eqs. 5, 25) support a claim that ALL eigenvalues of the equivalent chain oscillator are eigenvalues of the corresponding mechanistic model for \(\sigma =1/2\), and most importantly, the rightmost pair of eigenvalues is equal (\(\nu _{\mathrm{slow}} =\lambda _{\mathrm{slow}}\)). Even though we have no formal proof, the eigenvalue and energy equivalence seem to be true for the general, \(\sigma \ne 1/2\) case.

6 The energy flux function

For turbulent flows, the energy flux shows the rate of energy transfer at the different scales of eddies. An analogous quantity is defined for the mechanistic model. Similarly to the energy spectrum, a set of fluxes can be calculated, one for each wavenumber. The energy flux \({\varPi }_{l}(t)\) of level l is defined as the rate of energy transfer between levels l and \(l+1\), and it is calculated as

$$\begin{aligned} {\varPi }_{l}(t)={\varPi }_{l-1}(t)-{\dot{E}}_{l}(t),\quad l=1,\ldots ,n. \end{aligned}$$
(26)

Here \({\varPi }_{0}(t)=0\), since the top mass does not transfer any energy to the ceiling. Furthermore, we define the dissipation rate of the system as

$$\begin{aligned} \epsilon (t)=-{\dot{E}}(t). \end{aligned}$$
(27)

It can be shown that the recursive formula (26) leads to \({\varPi }_{l}(t)=-\sum _{i=1}^{l}{\dot{E}}_{i}(t)\) and \({\varPi }_{n}(t)=-\sum _{i=1}^{n}{\dot{E}}_{i}(t)=\epsilon (t)\).

Similarly to the mean energy, the mean dissipation rate of the system is also defined in the asymptotic limit:

$$\begin{aligned} {\bar{\epsilon }}=-\frac{\beta }{\pi }\int _{\tau }^{\tau +\pi /\beta }\dot{E}(t)\mathrm{d}t,\quad \tau \rightarrow \infty . \end{aligned}$$
(28)

The mean fluxes \(\bar{{\varPi }_{l}}\) are defined similarly for \(l=1,\ldots ,n\).

Following the framework of Sect. 4, we scale the mean fluxes with \({\bar{\epsilon }}\) (the mean level energies were scaled with \({\bar{E}}\)) to yield the scaled energy flux

$$\begin{aligned} {\hat{{\varPi }}}_{l}={\bar{{\varPi }}}_{l}/{\bar{\epsilon }},\quad l=1,\ldots ,n \end{aligned}$$
(29)

for a given mass wavenumber \(\kappa _{l}\). The \({\hat{{\varPi }}}_{l}\) values constitute the discrete energy flux function \({\hat{{\varPi }}}\) of the mechanistic model.

6.1 Derivation of the energy flux function

We are investigating the asymptotic behavior of the system. To perform the averaging in Eq. (28), we substitute the derivative of Eq. (16) in Eq. (28). The result is

$$\begin{aligned} {\bar{\epsilon }}=-e^{2\alpha \tau }\left( e^{2\alpha \frac{\pi }{\beta }}-1\right) \left( B_{1}+B_{2}\right) . \end{aligned}$$
(30)

The same averaging performed on the level fluxes yields

$$\begin{aligned} {\bar{{\varPi }}}_{l}=-e^{2\alpha \tau }\left( e^{2\alpha \frac{\pi }{\beta }}-1\right) \sum _{i=1}^{l}\left( B_{i,1}+B_{i,2}\right) , \end{aligned}$$
(31)

\(l=1,\ldots ,n\). The scaled level fluxes are calculated by substituting \({\bar{\epsilon }}\) and \({\bar{{\varPi }}}_{l}\) in Eq. (29), i.e.

$$\begin{aligned} {\hat{{\varPi }}}_{l}=\frac{\sum _{i=1}^{l}\left( B_{i,1}+B_{i,2}\right) }{B_{1}+B_{2} },\quad l=1,\ldots ,n. \end{aligned}$$
(32)

That is, we only need the constants \(B_{1}, B_{2}\), and \(B_{l,1}, B_{l,2}\) to calculate the energy flux function. In Sect. 4.1, we showed how these constants are related to the initial values \(E(0), {\dot{E}}(0), {\ddot{E}}(0)\), and substituting Eq. (21) in Eq. (32) leads to

$$\begin{aligned} {\hat{{\varPi }}}_{l}=\frac{\sum _{i=1}^{l}E_{i}(0)}{E(0)},\quad l=1,\ldots ,n. \end{aligned}$$
(33)

It follows from Eq. (33) that \({\hat{{\varPi }}}_{l}>{\hat{{\varPi }}}_{l-1}\) and \({\hat{{\varPi }}}_{n}=1\).

7 Results

First we compute and compare the energy spectrum of 10-level mechanistic models and their equivalent chain oscillators for different \(\sigma \) values. The results are shown in Fig. 6. These figures demonstrate that the energy spectrum of the mechanistic model and that of its equivalent chain oscillator are practically the same regardless of the value of \(\sigma \). This allows us to use the equivalent chain oscillator to calculate the energy spectrum of even larger systems.

Fig. 6
figure 6

Energy spectra of 10-level mechanistic models and their equivalent chain oscillators for a\(\sigma =0.48\), b\(\sigma =0.5\), c\(\sigma =0.52\)

Full size image
Fig. 7
figure 7

Energy spectra of 20-level mechanistic models for a\(\sigma =0.492\) (the slope of the straight line is \(\gamma =-1.662\)), b\(\sigma =0.5\), c\(\sigma =0.503\), d\(\sigma =0.505\), e\(\sigma =0.507\), and f\(\sigma =0.52\)

Full size image

The energy spectrum of the mechanistic model is calculated with different \(\sigma \) values using the equivalent chain oscillator formulation for \(n=20\) levels (Fig. 7).

For \(\sigma <1/2\) (Fig. 7a) the energy spectrum is similar to the Kolmogorov spectrum (cf. Fig. 1): The peak is located at a small wavenumber and the spectrum has a negative slope in the intermediate range. Figure 7b shows that the spectrum is almost symmetric for \(\sigma =1/2\) (the damping breaks the symmetry), and most energy is concentrated in the intermediate scales. For \(\sigma >1/2\) (Fig. 7c), the peak is further shifted toward large wavenumbers and the spectrum has a positive slope in the intermediate range. As \(\sigma \) is further increased, local minima appear in the spectrum (Fig. 7d, e). When \(\sigma \) is set even larger, the spectrum changes once more, and the shape depicted in Fig. 7f becomes typical.

In the \(\sigma <1/2\) case, we approximate the intermediate range of the spectrum with the scaling law \({\hat{E}}\sim \kappa ^{\gamma }\) (Fig. 7a, solid line). The main finding is that parameter \(\sigma \) can be tuned to match the Kolmogorov exponent: At \(\sigma \approx 0.492\), the exponent is \(\gamma =-5/3\), agreeing with the Kolmogorov exponent for 3D homogeneous isotropic turbulence.

It was also investigated how the energy spectrum behaves as the number of levels n changes. In Fig. 8, energy spectra for \(n=10, 15, 20, 25\) are depicted with different \(\sigma \)’s.

Fig. 8
figure 8

Energy spectra of n-level mechanistic models for a\(\sigma =0.492\), b\(\sigma =0.5\), and c\(\sigma =0.503\)

Full size image
Fig. 9
figure 9

a The four eigenvalues \(\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4}\) of the 20-level mechanistic model which compete to be the rightmost eigenvalue in the \(\sigma \in [0.48,0.52]\) range. b The eigenvalue \(\lambda _{2}\) overtakes \(\lambda {1}\). c The eigenvalue \(\lambda _{3}\) overtakes \(\lambda _{2}\) and then \(\lambda _{4}\) overtakes \(\lambda _{3}\)

Full size image

For \(\sigma <1/2\) (Fig. 8a), the energy spectrum gets extended to include the higher wavenumbers. For \(\sigma \ge 1/2\) (Fig. 8b, c), the change of the spectrum is more spectacular: The shape remains qualitatively the same, but the whole spectrum gets stretched to include the higher wavenumbers. This is not just an extension to higher wavenumbers, since the peak is also shifted significantly toward the larger wavenumbers. In the \(\sigma >1/2\) case, it is also possible that the shape of the spectrum changes. For example, in Fig. 8c the \(n=25\) case exhibits a different spectrum shape compared to the other three cases. This change is similar to how the spectrum changes as \(\sigma \) is increased (see Fig. 7c, d).

The changes in the shape of the energy spectrum for the \(\sigma >1/2\) cases (Fig. 7c–f) are due to the change in the order of the rightmost eigenvalues and the accompanying significant change of the eigenvector \({\mathbf {s}}_{\mathrm{slow}}\). The same happens when a \(\sigma \) value is given and n is increased as shown in Fig. 8c. In Fig. 9, the real part of four eigenvalues (denoted by \(\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4}\)) of the 20-level mechanistic model is plotted as the function of \(\sigma \). This figure illustrates how these eigenvalues—together with their complex conjugate—“compete” with each other to be the rightmost eigenvalue \(\lambda _{\mathrm{slow}}\). Since rightmost refers to the location of the eigenvalue in the complex plane, the rightmost eigenvalue has the largest real part. For \(\sigma \le 1/2\), the rightmost eigenvalue is \(\lambda _{\mathrm{slow}}=\lambda _{1}\). As \(\sigma \) is increased, the rightmost eigenvalue changes three times in the investigated \(\sigma \) range (\(\sigma \in [0.48,0.52]\)). Figure 9b, c shows the boxed parts of Fig. 9a in detail. One can see that \(\lambda _{2}, \lambda _{3}\), and \(\lambda _{4}\) become rightmost one after the other. The real part of the eigenvectors corresponding to these four eigenvalues is depicted in Fig. 10 for \(\sigma =0.503\) (the equivalent chain oscillator was used here). These eigenvectors have a very different shape. This is why the energy spectrum changes significantly, when the rightmost eigenvalue changes.

Fig. 10
figure 10

The real part of the four eigenvectors corresponding to a\(\lambda _{1}\), b\(\lambda _{2}\), c\(\lambda _{3}\), and d\(\lambda _{4}\) for \(\sigma =0.503\)

Full size image

We also computed the energy flux function of different mechanistic models. Figure 11 shows energy flux functions for different n’s and \(\sigma \)’s. As expected, the energy flux functions are monotonously increasing. The maximum is \({\hat{{\varPi }}}_{n}=1\) which simply means that the energy flux between the last level and the fixed ground is the dissipation rate of the system. Figure 11a shows the energy flux functions corresponding to the \(\sigma <1/2\) case. In this case, the energy spectrum is Kolmogorov-like (see Figs. 6a, 7a, and 8a), while the energy flux function is nearly constant (slightly increasing) from the intermediate range to the largest wavenumber. This is as intriguing as the shape of the energy spectrum itself, since the energy flux is constant in 3D homogeneous isotropic turbulence through the inertial range.

Fig. 11
figure 11

Energy flux functions of n-level mechanistic models for a\(\sigma =0.492\), b\(\sigma =0.5\), c\(\sigma =0.503\)

Full size image

8 Conclusions and future work

Inspired by Richardson’s eddy hypothesis, we introduced a mechanistic model of turbulence with different mass scales. The discrete energy spectrum of the model was defined as the fraction of the total energy stored in the different mass scales. A formula (Eq. 22) was derived to calculate this spectrum in the asymptotic limit. Similarly, the discrete energy flux function of the system was defined as the set of energy fluxes between levels scaled by the dissipation rate. A decimation procedure was applied to yield an equivalent chain oscillator with energy spectrum identical to that of the mechanistic model. This enabled the calculation of the energy spectrum and energy flux for many-level systems. In the \(\sigma <1/2\) case, the energy spectrum is qualitatively similar to the Kolmogorov spectrum of 3D turbulence. Moreover, \(\sigma \) can be tuned so that the exponent \(\gamma \) of the energy spectrum precisely matches with that of the Kolmogorov spectrum. Furthermore, in this case the energy flux function is practically constant through the intermediate range.

This work is expected to motivate new studies connecting eigenvalue distributions of infinite-dimensional linear systems with energy transfer and resonance capture in nonlinear systems. In future work, the model will be extended to include nonlinearities (e.g., nonlinear energy sinks at the bottom level instead of linear tuned mass dampers), cascade asymmetry (mistuned masses), and instability at the large scales (e.g., negative damping could be added to the system). We also want to study the system with continuous energy pumping at the large or some intermediate scales (this latter would correspond to the case of 2D isotropic turbulence [38, 39]) via external forcing.