A note on the “nonlinear control of electrical flexible-joint robots”

Abstract

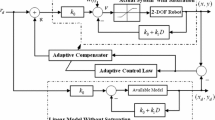
Robust tracking control of electrically flexible-joint robots is addressed in this paper. Two important practical situations are considered. The fact that robot actuators have limited voltage and that current measurement is subjected to noise. Let us notice that a few solutions for the voltage-bounded robust tracking control have been proposed. In this paper, we contribute to this subject by presenting a new form of voltage-based control strategy. It proves that the closed loop system is BIBO stable, while actuator/link position errors are uniformly–ultimately bounded stable in agreement with Lyapunov’s direct method in any finite region of the state space. As a second contribution of this paper, we present a robust adaptive control scheme without the need for computation of regressor matrix and current measurement, with the same result on the closed loop system stability. This novelty gives a simple robust tracking control scheme for both structured and unstructured uncertainties based on the function approximation technique. The analytical studies as well as experimental results produced using MATLAB/Simulink external mode control on a flexible-joint electrically driven robot demonstrate high performance of the proposed control scheme.

Appendices

Appendix 1

Proof is as same as those defined by Fateh [16]. Pre-multiplying both sides of (3) by $I_\mathrm{a}^T$, one obtains the following power equation

$$\begin{aligned} I_\mathrm{a}^T v(t)=I_\mathrm{a}^T L_\mathrm{a} \dot{I}_\mathrm{a} +I_\mathrm{a}^T R_\mathrm{a} I_\mathrm{a} +I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} +I_\mathrm{a}^T \varphi (t) \end{aligned}$$

(73)

or equivalently

$$\begin{aligned} I_\mathrm{a}^T v(t)= & {} \sum _{j=1}^n {L{_\textit{ajj}} I_{aj} \dot{I}_{aj} } +\sum _{j=1}^n {R_{\textit{ajj}} I_{aj}^2 }\nonumber \\&+\,I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} +I_\mathrm{a}^T \varphi (t) \end{aligned}$$

(74)

where j and jj indices denote the jth elements of a vector and a diagonal matrix, respectively. Equation (74) can be translated as follows. Actuators receive the electrical power expressed by $I_\mathrm{a}^\mathrm{T} v(t)$ to provide the mechanical power stated as $I_\mathrm{a}^\mathrm{T} K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}}$ in (74). The power $\mathop \sum \nolimits _{j=1}^n {R_{\textit{ajj}} I_{aj}^2 }$ is the loss in the windings, and the power $\mathop \sum \nolimits _{j=1}^n {L_{\textit{ajj}} I_{aj} \dot{I}_{aj} }$ is the time derivative of the magnetic energy. From (74), we can write for $t\ge 0$

$$\begin{aligned} \mathop \int \limits _0^t {I_\mathrm{a}^T (v(\tau )-\varphi (\tau ))\mathrm{d}\tau }= & {} \sum _{j=1}^n {\mathop \int \limits _0^t {L_{\textit{ajj}} I_{aj} \dot{I}_{aj} \mathrm{d}\tau } }\nonumber \\&+\,\sum _{j=1}^n {\mathop \int \limits _0^t {R_{\textit{ajj}} I_{aj}^2 \mathrm{d}\tau } }\nonumber \\&+\,\mathop \int \limits _0^t {I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} \mathrm{d}\tau } \end{aligned}$$

(75)

With $I_{aj} (0)=0$, for $j=1,2,\ldots ,n$, (75) is

$$\begin{aligned}&\mathop \int \limits _0^t {I_\mathrm{a}^T (v(\tau )-\varphi (\tau ))\mathrm{d}\tau } =0.5\sum _{j=1}^n {L_{\textit{ajj}} I_{aj}^2 }\nonumber \\&\quad +\,\sum _{j=1}^n {R_{\textit{ajj}} I_{aj}^2 t} +\,\mathop \int \limits _0^t {I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} \mathrm{d}\tau } \end{aligned}$$

(76)

Since $\mathop \sum \nolimits _{j=1}^n {R_{\textit{ajj}} I_{aj}^2 t} \ge 0$ and $\mathop \sum \nolimits _{j=1}^n{L_{\textit{ajj}} I_{aj}^2 } \ge 0$

$$\begin{aligned} \mathop \int \limits _0^t {I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} \mathrm{d}\tau } \le \mathop \int \limits _0^t {I_\mathrm{a}^T (v(\tau )-\varphi (\tau ))\mathrm{d}\tau } \end{aligned}$$

(77)

The upper bound of mechanical energy is given by

$$\begin{aligned} \mathop \int \limits _0^t {I_\mathrm{a}^T K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} \mathrm{d}\tau } =\mathop \int \limits _0^t {I_\mathrm{a}^T (v(\tau )-\varphi (\tau ))\mathrm{d}\tau } \end{aligned}$$

(78)

Hence, at the upper bound of mechanical energy

$$\begin{aligned} K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} =v(t)-\varphi (t) \end{aligned}$$

(79)

Therefore, $\dot{\theta }_{\mathrm{m}}$ is limited as

$$\begin{aligned} \left\| {K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} } \right\| \le \left\| {v(t)} \right\| +\left\| {\varphi (t)} \right\| \end{aligned}$$

(80)

From Remark 1, Assumptions 1 and 2, we have

$$\begin{aligned} \left\| {\dot{\theta }_{\mathrm{m}} } \right\| \le \underline{k_{\mathrm{b}} }^{-1}\left( u_{\mathrm{max} } +\varphi _{\mathrm{max} } \right) \buildrel \Delta \over = \xi _{\dot{\theta }_{\mathrm{m}} } \end{aligned}$$

(81)

where $\xi _{\dot{\theta }_{\mathrm{m}} }$ is the maximum value of motor joint velocity vector. From (3), we can write

$$\begin{aligned} L_\mathrm{a} \dot{I}_\mathrm{a} +R_\mathrm{a} I_\mathrm{a} =\omega \end{aligned}$$

(82)

where

$$\begin{aligned} \omega =v(t)-K_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} -\varphi (t) \end{aligned}$$

(83)

is bounded, whereas $v(t),\,\dot{\theta }_{\mathrm{m}}$, and $\varphi (t)$ are bounded as stated by Remark 1, (81), and Assumption 2, respectively. Consequently, the input $\omega$ in (82) is bounded. The linear differential equation (82) is stable linear system based on the Routh–Hurwitz criterion. Since the input $\omega$ is bounded, the output $I_\mathrm{a}$ is bounded as $\xi _{I_\mathrm{a} }$. From (82), we can write

$$\begin{aligned} L_\mathrm{a} \dot{I}_\mathrm{a} =\omega -R_\mathrm{a} I_\mathrm{a} \end{aligned}$$

(84)

Since $\omega$ and $I_\mathrm{a}$ are bounded, then $\dot{I}_\mathrm{a}$ is bounded as $\xi _{\dot{I}_\mathrm{a} }$.

Appendix 2

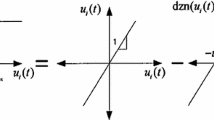
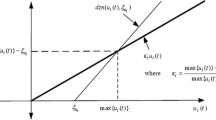
Proof is as same as [18]. Suppose that $u_i (t)$ is the ith value of u(t) vector. If $u_i (t)$ exist within $[-\mathrm{max} \{u_i (t)\},\mathrm{max} \{u_i (t)\}]$ and $\delta _i$ becomes $\frac{\mathrm{max} \{u_i (t)\}-u_{i_{\mathrm{max} } } }{\mathrm{max} \{u_i (t)\}},\left| {\mathrm{d}zn(u_i (t),u_{i_{\mathrm{max} } } )} \right| \le \delta _i \left| {u_i (t)} \right|$ is satisfied by Fig. 12. From Fig. 12, $\mathrm{d}zn(u(t),u_{\mathrm{max} } )$ is bounded as the following inequality:

$$\begin{aligned} \left\| {\mathrm{d}zn(u(t),u_{\mathrm{max} } )} \right\| \le \delta \left\| {u(t)} \right\| \end{aligned}$$

(85)

where

$$\begin{aligned} \delta =\mathop {\mathrm{max} }\limits _i \left\{ {1-\frac{u_{i_{\mathrm{max} } } }{u_i (t)}} \right\} \end{aligned}$$

(86)

According to (14), the magnitude of the control input is bounded as follows:

$$\begin{aligned} \left\| {u(t)} \right\| \le \bar{{r}}_\mathrm{a} \xi _{I_\mathrm{a} } +\left\| {\hat{{K}}_{\mathrm{b}} (\dot{\theta }_{\mathrm{md}} -\beta e)} \right\| \end{aligned}$$

(87)

Thus, from Eqs. (85) and (87), $\left\| {\mathrm{d}zn(\cdot )} \right\|$ is satisfied with the following condition:

$$\begin{aligned}&\left\| {\mathrm{d}zn(u(t),u_{\mathrm{max} } )} \right\| \le \delta \left\| {u(t)} \right\| \nonumber \\&\quad \le \,\delta \left( \bar{{r}}_\mathrm{a} \xi _{I_\mathrm{a} }+\,\left\| {\hat{{K}}_{\mathrm{b}} (\dot{\theta }_{\mathrm{md}} -\beta e)} \right\| \right) \end{aligned}$$

Fig. 12

Linear bound of dead-zone function

Appendix 3

Considering to (16) we have

$$\begin{aligned}&\left\| {\hat{{K}}_{\mathrm{b}} (\dot{\theta }_{\mathrm{md}} -\beta e)} \right\| \le \left\| {\mathrm{d}zn(u(t),u_{\mathrm{max} } )} \right\| +\left\| L_\mathrm{a} \dot{I}_\mathrm{a} (t)\right. \nonumber \\&\quad \left. +\hat{{K}}_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} -\tilde{p}^{\mathrm{T}}y+\varphi (t)\right\| \end{aligned}$$

(88)

Now, assume that $\left\| {L_\mathrm{a} \dot{I}_\mathrm{a} (t)+\hat{{K}}_{\mathrm{b}} \dot{\theta }_{\mathrm{m}} -\tilde{p}^{\mathrm{T}}y+\varphi (t)} \right\| \le \rho$, where $\rho >0$ is a known scalar defined by the use of Lemma 1, and Assumptions 1 and 2. Thus:

$$\begin{aligned}&\left\| {\hat{{K}}_{\mathrm{b}} (\dot{\theta }_{\mathrm{md}} -\beta e)} \right\| \le \delta \left( \bar{{r}}_\mathrm{a} \xi _{I_\mathrm{a} } +\left\| {\hat{{K}}_{\mathrm{b}} (\dot{\theta }_{\mathrm{md}} -\beta e)} \right\| \right) +\rho \nonumber \\ \end{aligned}$$

(89)

This completes the proof. $\square$

Appendix 4

Proof is based on Gershgorin theorem and is similar to that in [17] when $\alpha _1 =\alpha _2 =\mu$. Let T be a transformation such that

$$\begin{aligned} D_i =T\varLambda T^{-1} \end{aligned}$$

(90)

where $\varLambda =\mathrm{diag}\{a_1 ,a_2 ,\ldots ,a_{\mathrm{n}} \}$ and the $a_i$ are the eigenvalues of $D_i$. It follows that:

$$\begin{aligned}&\left[ {{\begin{array}{ccc} T&{}\quad 0&{}\quad 0\\ 0&{}\quad T&{}\quad 0\\ 0&{}\quad 0&{}\quad T\\ \end{array} }} \right] {{\varvec{P}}}\left[ {{\begin{array}{ccc} {T^{-1}}&{}\quad 0&{}\quad 0\\ 0&{}\quad {T^{-1}}&{}\quad 0\\ 0&{}\quad 0&{}\quad {T^{-1}}\\ \end{array} }} \right] \nonumber \\&\quad = \frac{1}{2}\left[ {{\begin{array}{ccc} {\mu K_{\mathrm{p}} +\mu K_I +\mu ^{2}\varLambda }&{}\quad {\mu K_{\mathrm{d}} +K_I +\mu ^{2}\varLambda }&{}\quad {\mu \varLambda }\\ {\mu K_{\mathrm{d}} +K_I +\mu ^{2}\varLambda }&{}\quad {\mu K_{\mathrm{d}} +K_{\mathrm{p}} +\mu ^{2}\varLambda }&{}\quad {\mu \varLambda }\\ {\mu \varLambda }&{}\quad {\mu \varLambda }&{}\quad \varLambda \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(91)

where all the sub-matrices on the right-hand side of the previous equation are diagonal. By the Gershgorin theorem, we know that the eigenvalues $\aleph _j , j=1,{\ldots },3n$, of the matrix on the right-hand side of (91) satisfy the following inequalities

$$\begin{aligned}&\left| {\aleph _i -\frac{1}{2}(\mu k_{pi} +\mu k_{Ii} +\mu ^{2}a_i )} \right| \nonumber \\&\quad \le \frac{1}{2}\left( \mu k_{di} +k_{Ii} +\mu ^{2}a_i +\mu a_i \right) \nonumber \\&\left| {\aleph _{n+i} -\frac{1}{2}\left( \mu k_{di} +k_{pi} +\mu ^{2}a_i \right) } \right| \nonumber \\&\quad \le \frac{1}{2}\left( \mu k_{di} +k_{Ii} +\mu ^{2}a_i +\mu a_i \right) \nonumber \\&\left| {\aleph _{2n+i} -\frac{1}{2}a_i } \right| \le \mu a_i, \quad {i=1,2,\ldots ,n} \end{aligned}$$

(92)

Or equivalently

$$\begin{aligned}&\mu (k_{pi} -k_{di} )+(\mu -1)k_{Ii} -\mu a_i \le 2\aleph _i \le (1+\mu )k_{Ii}\nonumber \\&\quad +\,\mu (k_{pi}+k_{di} )+\mu (1+2\mu )a_i \nonumber \\&\quad k_{pi}-k_{Ii} -\mu a_i \le 2\aleph _{n+i} \le k_{pi} +2\mu k_{di} +k_{Ii}\nonumber \\&\quad +\,\mu (1+2\mu )a_i\hbox { }\nonumber \\&\quad (1-2\mu )a_i \le 2\aleph _{2n+i} \le (1+2\mu )a_i \end{aligned}$$

(93)

for $i=1,{\ldots },n$. The proof of the lemma can be completed by noting that $\bar{{r}}_{\mathrm{g}} ^{-1}\bar{{k}}^{-1}d_{\mathrm{m}} \le a_i \le \underline{r_{\mathrm{g}} }^{-1}\underline{k}^{-1}d_{\mathrm{M}} , \underline{\lambda }(K_{\mathrm{p}} )\le k_{pi} \le \bar{{\lambda }}(K_{\mathrm{p}} ), \underline{\lambda }(K_{\mathrm{d}} )\le k_{di} \le \bar{{\lambda }}(K_{\mathrm{d}} )$, and $\underline{\lambda }(K_I )\le k_{Ii} \le \bar{{\lambda }}(K_I )$ for $i=1,2,\ldots ,n$. It is worthy to mention that similar proof techniques can be found in [26, 27]. $\square$