Skip to main content
SpringerLink
Log in

Multiple-soliton solutions, soliton-type solutions and rational solutions for the \(\varvec{(3+1)}\)-dimensional generalized shallow water equation in oceans, estuaries and impoundments

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

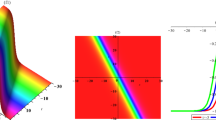
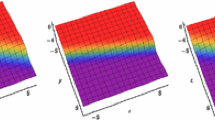
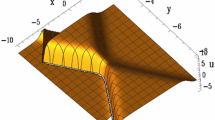
The Hirota bilinear method and Painlevé–Bäcklund transformation are used to discuss the soliton solutions of the \((3+1)\)-dimensional generalized shallow water equation. With the help of symbolic computation, multiple-soliton solutions, multiple singular soliton solutions, hyperbolic function solutions and trigonometric function solutions are formally obtained. These soliton solutions possess abundant physical architectures. The graphs corresponding to these solutions show the particular localized excitations and the interactions between two solitary waves and three solitary waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Liu, J.G., Zeng, Z.F.: Multiple soliton solutions, soliton-type solutions and rational solutions for the \((3+1)\)-dimensional potential-YTSF equation. Indian J. Pure Appl. Math. 45, 989–1002 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  2. Zuo, D.W., Gao, Y.T., Meng, G.Q., Shen, Y.J., Yu, X.: Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system. Nonlinear Dyn. 75(4), 1–8 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  3. Liu, D.Y., Tian, B., Jiang, Y., Sun, W.R.: Soliton solutions and Bäcklund transformations of a \((2+1)\)-dimensional nonlinear evolution equation via the Jaulent–Miodek hierarchy. Nonlinear Dyn. 78(4), 2341–2347 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Mirzazadeh, M., Arnous, A.H., Mahmood, M.F., Zerrad, E., Biswas, A.: Soliton solutions to resonant nonlinear Schrödinger’s equation with time-dependent coefficients by trial solution approach. Nonlinear Dyn. 81(1–2), 1–6 (2015)

    MathSciNet  Google Scholar 

  5. Mirzazadeh, M.: Soliton solutions of Davey–Stewartson equation by trial equation method and ansatz approach. Nonlinear Dyn. 82(4), 1775–1780 (2015)

    Article  MathSciNet  Google Scholar 

  6. Zhang, L., Lin, Y.: Symbolic computation of exact solutions for nonlinear evolution equations. Nonlinear Dyn. 79(2), 823–833 (2014)

    Article  Google Scholar 

  7. Rajan, M.S.M., Mahalingam, A.: Nonautonomous solitons in modified inhomogeneous Hirota equation: soliton control and soliton interaction. Nonlinear Dyn. 79(4), 2469–2484 (2014)

    Article  MathSciNet  Google Scholar 

  8. Jiang, H.J., Xiang, J.J., Dai, C.Q., Wang, Y.Y.: Nonautonomous bright soliton solutions on continuous wave and cnoidal wave backgrounds in blood vessels. Nonlinear Dyn. 75(1–2), 201–207 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering Transform. Cambridge University Press, London (1990)

    MATH  Google Scholar 

  10. Sakthivel, R., Chun, C., Lee, J.: New travelling wave solutions of Burgers equation with finite transport memory. Z. Naturforsch. A. 65, 633–640 (2010)

    Google Scholar 

  11. Hirota, R.: Exact solutions of the Korteweg–de Vries equation for multiple collision of solitons. Phys. Rev. Lett. 27, 1192–1194 (1971)

    Article  MATH  Google Scholar 

  12. Xie, T.C., Li, B., Zhang, H.Q.: New explicit and exact solutions for the Nizhnik–Novikov–Vesselov equation. Appl. Math. E-Notes 1, 139–142 (2001)

    MathSciNet  MATH  Google Scholar 

  13. Fan, E., Zhang, H.: A note on the homogeneous balance method. Phys. Lett. A. 246, 403–406 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  14. Fan, E.: Two new applications of the homogeneous balance method. Phys. Lett. A. 265, 353–357 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  15. Senthilvelan, M.: On the extended applications of homogeneous balance method. Appl. Math. Comput. 123, 381–388 (2001)

    MathSciNet  MATH  Google Scholar 

  16. Zhang, S.: The periodic wave solutions for the \((2+1)\) dimensional Konopelchenko–Dubrovsky equations. Chaos Solitons Fractals 30, 1213–1220 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. El-Sabbagh, M.F., Ali, A.T.: Nonclassical symmetries for nonlinear partial differential equations via compatibility. Commun. Theor. Phys. 56, 611–616 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. El-Sabbagh, M.F., Hasan, M.M., Hamed, E.: The Painlevé property for some nonlinear evolution equations. In: Proceedings of France–Egypt Mathematical Conference, Cairo, 3–5 May 2010

  19. El-Sabbagh, M.F., Ali, A.T., El-Ganaini, S.: New abundant exact solutions for the system of \((2+1)\)-dimensional Burgers equations. Appl. Math. Inform. Sci. 2(1), 31–41 (2008)

    MathSciNet  MATH  Google Scholar 

  20. Bai, C.J., Zhao, H., Xu, H.Y., Zhang, X.: New traveling wave solutions for a class of nonlinear evolution equations. Int. J. Mod. Phys. B. 25, 319–327 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Zayed, E.M.E., Gepreel, K.A.: The \((G^{\prime }/G)\)-expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics. J. Math. Phys. 50, 013502 (2009)

    Article  MathSciNet  Google Scholar 

  22. Kim, H., Sakthivel, R.: New exact traveling wave solutions of some nonlinear higher-dimensional physical models. Rep. Math. Phys. 70, 39–50 (2012)

    Article  MathSciNet  Google Scholar 

  23. Dai, Z.D., Lin, S.Q., Fu, H.M., Zeng, X.P.: Exact three-wave solutions for the KP equation. Appl. Math. Comput. 216(5), 1599–1604 (2010)

    MathSciNet  MATH  Google Scholar 

  24. Wang, C.J., Dai, Z.D., Mu, G., Lin, S.Q.: New exact periodic solitary-wave solutions for new \((2+1)\)-dimensional KdV equation. Commun. Theor. Phys. 52, 862–864 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zeng, X.P., Dai, Z.D., Li, D.L.: New periodic soliton solutions for the \((3+1)\)-dimensional potential-YTSF equation. Chaos Solitons Fractls 42, 657–661 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Dai, Z.D., Li, S.L., Dai, Q.Y., Huang, J.: Singular periodic soliton solutions and resonance for the Kadomtsev–Petviashvili equation. Chaos Solitons Fractls 34(4), 1148–1153 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dai, Z.D., Liu, Z.J., Li, D.L.: Exact periodic solitary-wave solution for KdV equation. Chin. Phys. Lett. A. 25(5), 1151–1153 (2008)

    Google Scholar 

  28. Dai, Z.D., Huang, J., Jiang, M.R., Wang, S.H.: Homoclinic orbits and periodic solitons for Boussinesq equation with even constraint. Chaos Solitons Fractls 26, 1189–1194 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. Tian, B., Gao, Y.T.: Beyond travelling waves: a new algorithm for solving nonlinear evolution equations. Comput. Phys. Commun. 95, 139–142 (1996)

    Article  MATH  Google Scholar 

  30. Zayed, E.M.E.: Traveling wave solutions for higher dimensional nonlinear evolution equations using the \((G^{\prime }/G)\)-expansion method. J. Appl. Math. Inform. 28, 383–395 (2010)

    MATH  Google Scholar 

  31. Tang, Y.N., Ma, W.X., Xu, W.: Grammian and Pfaffian solutions as well as Pfaffianization for a \((3+1)\)-dimensional generalized shallow water equation. Chin. Phys. B. 21(7), 070212 (2012)

    Article  Google Scholar 

  32. Wazwaz, A.M.: Multiple soliton solutions and multiple singular soliton solutions for \((2+1)\)-dimensional shallow water wave equations. Phys. Lett. A. 373, 2927–2930 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wazwaz, A.M., El-Tantawy, S.A.: A new integrable \((3+1)\)-dimensional KdV-like model with its multiple-soliton solutions. Nonlinear. Dyn. 373, 1–6 (2015)

    MathSciNet  Google Scholar 

  34. Wazwaz, A.M.: New \((3+1)\)-dimensional nonlinear evolution equations with mKdV equation constituting its main part: multiple soliton solutions. Chaos Solitons Fractls 76, 93–97 (2015)

    Article  MathSciNet  Google Scholar 

  35. Wazwaz, A.M.: A study on a \((2+1)\)-dimensional and a \((3+1)\)-dimensional generalized Burgers equation. Appl. Math. Lett. 31, 41–45 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Ma, W.X., Zhu, Z.: Solving the \((3+1)\)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 218(24), 11871–11879 (2012)

    MathSciNet  MATH  Google Scholar 

  37. Alnowehy, A.G.: The multiple exp-function method and the linear superposition principle for solving the \((2+1)\)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Z. Naturforsch. A. 70(9), 775–779 (2015)

    Google Scholar 

  38. Ma, W.X., Huang, T., Zhang, Y.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82(6), 065003 (2010)

    Article  MATH  Google Scholar 

  39. Wazwaz, A.M.: Multiple-soliton solutions for the Calogero–Bogoyavlenskii–Schiff, Jimbo–Miwa and YTSF equations. Appl. Math. Comput. 203, 592–597 (2008)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We would like to thank Editor, the Referees for their timely and valuable comments.

Author information

Authors and Affiliations

  1. Department of Basic, Jiangxi Vocational and Technical College of Communication, Nanchang, 330013, Jiangxi, China

    Zhi-Fang Zeng

  2. College of Computer, Jiangxi University of Traditional Chinese Medicine, Nanchang, 330004, Jiangxi, China

    Jian-Guo Liu & Bin Nie

Authors
  1. Zhi-Fang Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian-Guo Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bin Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian-Guo Liu.

Additional information

Project supported by National Natural Science Foundation of China (Grant No. 61562045).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zeng, ZF., Liu, JG. & Nie, B. Multiple-soliton solutions, soliton-type solutions and rational solutions for the \(\varvec{(3+1)}\)-dimensional generalized shallow water equation in oceans, estuaries and impoundments. Nonlinear Dyn 86, 667–675 (2016). https://doi.org/10.1007/s11071-016-2914-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2914-y

Keywords

Mathematics Subject Classification

Search

Navigation