Skip to main content
SpringerLink
Log in

Nonlinear free vibration of a rotating circular plate under the static load in magnetic field

  • Original Article
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

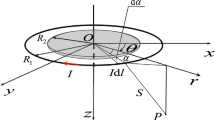
The nonlinear free vibration of a conductive rotating thin circular plate subjected to static loads in magnetic field was investigated. The nonlinear vibration equations of the motion on a spinning circular thin plate were derived. According to the set of a displacement function, the approximate solution of the static problem and the magneto elastic axisymmetric vibration differential equation of the round plate were obtained through the application of Galerkin integral method. The characteristic formula between nonlinear frequency and amplitude using the static load as a parameter was obtained by the method of multiple scales. According to the numerical calculation, the characteristic curves of the relationship between frequency and the parameter such as the static load, the magnetic induction intensity and the speed of rotation were obtained. The nonlinear vibration characteristics of a spinning plate with clamped boundary condition were described according to the curves drawn by Matlab. We also showed that different parameters (including magnetic induction intensity, static load, time and spinning velocity.) have effect on the frequency of the plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Shu, X.F., Zhang, X.Q., Zhang, J.X.: Thermoelastic free vibration of clamped circular plate. Appl. Math. Mech. Engl. Ed. 21(6), 715–724 (2000)

    Article  MATH  Google Scholar 

  2. Hu, Y.D., Zhang, Z.Q.: The bifurcation analysis on the circular functionally graded plate with combination resonances. Nonlinear Dyn. 67, 1779–1790 (2012)

    Article  MathSciNet  Google Scholar 

  3. Vogl, G.W., Nayfeh, A.H.: Primary resonance excitation of electrically actuated clamped circular plates. Nonlinear Dyn. 47, 181–192 (2007)

    Article  MATH  Google Scholar 

  4. Camier, C., Touzé, C., Thomas, O.: Non-linear vibrations of imperfect free-edge circular plates and shells. Eur. J. Mech. A Solids 28, 500–515 (2009)

    Article  MATH  Google Scholar 

  5. Hashemi, S.H., Farhadi, S., Carra, S.: Free vibration analysis of rotating thick plates. J. Sound Vib. 323(1–2), 366–384 (2009)

    Article  Google Scholar 

  6. Yeh, J.Y.: Free vibration analysis of rotating polar orthotropic annular plate with ER damping treatment. Compos. Part B 42, 781–788 (2011)

    Article  Google Scholar 

  7. Malekzadeh, P., Heydarpour, Y.: Free vibration analysis of rotating functionally graded truncated conical shells. Compos. Struct. 97, 176–188 (2013)

    Article  Google Scholar 

  8. Wang, Z.M., Wang, Z., Zhang, R.: Transverse vibration analysis of spinning circular plate based on differential quadrature method. J. Vib. Shock 33(1), 125–129 (2014)

    Google Scholar 

  9. Nayfeh, A.H., Jilani, A., Manzione, P.: Transverse vibrations of a centrally clamped rotating circular disk. Nonlinear Dyn. 26, 163–178 (2001)

    Article  MATH  Google Scholar 

  10. Du, G.J., Ma, J.Q.: Nonlinear vibration and buckling of circular sandwich plate under complex load. Appl. Math. Mech. Engl. Ed. 28(8), 1081–1091 (2007)

    Article  MATH  Google Scholar 

  11. Du, G.J., Li, H.J.: Nonlinear vibration of circular sandwich plate under the uniformed load. Appl. Math. Mech. Engl. Ed. 21(2), 217–226 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  12. Yuan, H., Liu, R.H.: Nonlinear vibration of corrugated shallow shells under uniform load. Appl. Math. Mech. Engl. Ed. 28(5), 514–520 (2007)

    Article  MATH  Google Scholar 

  13. Panda, S.K., Mahapatra, T.R.: Nonlinear finite element analysis of laminated composite spherical shell vibration under uniform thermal loading. Meccanica 49, 191–213 (2014)

  14. Hu, Y.D., Li, J.: Magneto-elastic combination resonances analysis of current-conducting thin plate. Appl. Math. Mech. Engl. Ed. 29(8), 1053–1066 (2008)

    Article  MATH  Google Scholar 

  15. Hu, Y.D., Li, J.: The magneto-elastic sub harmonic resonances of current-conducting thin plate in magnetic field. J. Sound Vib. 319(3–5), 1107–1120 (2009)

    Google Scholar 

  16. Helmut, F.B., Werner, E.: Transverse vibration and stability of spinning circular plates of constant thickness and different boundary conditions. J. Sound Vib. 300(3–5), 877–895 (2007)

    Google Scholar 

  17. Gorman, D.G., Lee, C.K., Reese, J.: Vibration analysis of a thin circular plate influenced by liquid/gas interaction in a cylindrical cavity. J. Sound Vib. 279(3–5), 601–608 (2005)

    Article  Google Scholar 

  18. Chen, Y.R., Chen, L.W.: Vibration and stability of rotating polar orthotropic sandwich annular plates with a viscoelastic core layer. Compos. Struct. 78, 45–57 (2007)

    Article  Google Scholar 

  19. Hu, Y.D., Du, G.J.: Forced vibration of a thin round conductive plate in magnetic field. Eng. Mech. 24(7), 184–188 (2007). (in Chinese)

    Google Scholar 

  20. Xu, Z.L.: Elasticity. Higher Education Press, Beijing (2006). (in Chinese)

    Google Scholar 

Download references

Acknowledgments

This project was supported by the National Natural Science Foundation of China (11472239), Hebei Provincial Natural Science Foundation of China (No. A2015203023) and the Key project of Science and technology Research of Higher Education of Hebei Province of China (ZD20131055).

Author information

Authors and Affiliations

  1. Hebei Provincial Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures, Yanshan University, Qinhuangdao, 066004, China

    Y. D. Hu & T. Wang

Authors
  1. Y. D. Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. D. Hu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, Y.D., Wang, T. Nonlinear free vibration of a rotating circular plate under the static load in magnetic field. Nonlinear Dyn 85, 1825–1835 (2016). https://doi.org/10.1007/s11071-016-2798-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2798-x

Keywords

Search

Navigation